广东省深圳市东北师范大学附属中学深圳学校2024届高三下学期适应性考试数学试题(PDF版无答案)
文档属性
| 名称 | 广东省深圳市东北师范大学附属中学深圳学校2024届高三下学期适应性考试数学试题(PDF版无答案) | 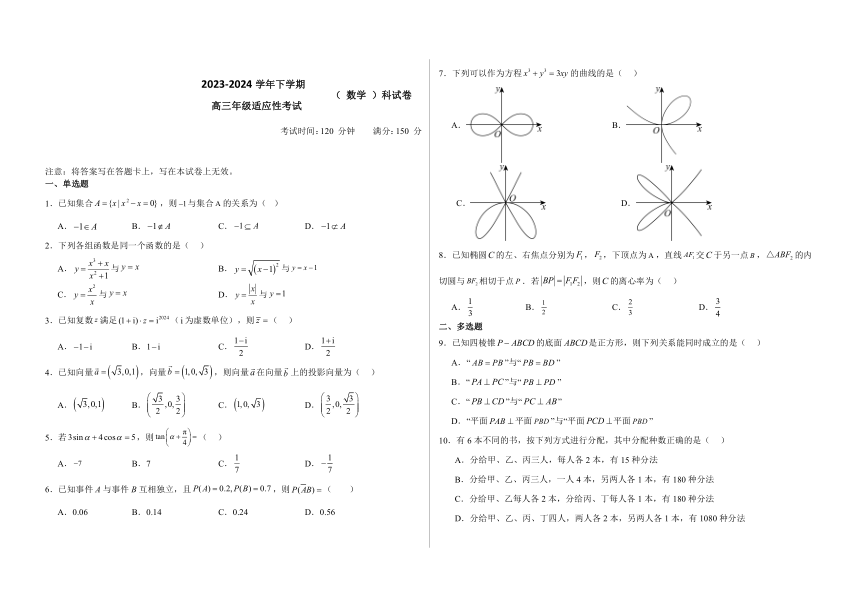 | |
| 格式 | |||
| 文件大小 | 523.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 07:43:30 | ||
图片预览

文档简介
7.下列可以作为方程 x3 y3 3xy的曲线的是( )
2023-2024 学年下学期
( 数学 )科试卷
高三年级适应性考试
A. B.
考试时间:120 分钟 满分:150 分
注意:将答案写在答题卡上,写在本试卷上无效。
一、单选题
1.已知集合 A {x | x 2 x 0},则 1与集合A的关系为( ) C. D.
A. 1 A B. 1 A C. 1 A D. 1 A
2.下列各组函数是同一个函数的是( )
8.已知椭圆C的左、右焦点分别为 F1, F2,下顶点为A,直线 AF1交C于另一点 B,△ABF3 2 的内
A y x x. 与 y x2 B. y x 1
2
与 y x 1
x 1
切圆与 BF2相切于点 P.若 BP F1F2 ,则C的离心率为( )
C y x
2 x
. 与 y x D. y 与 y 1
x x 1A B 1 C 2
3
. . .
3 2 3
D.
4
3.已知复数 z满足 (1 i) z i2024 ( i为虚数单位),则 z ( )
二、多选题
1 i 1 i
A. 1 i B.1 i C. D. 9.已知四棱锥 P ABCD的底面 ABCD是正方形,则下列关系能同时成立的是( )
2 2
A.“ AB PB ”与“ PB BD ”
4.已知向量 a 3,0,1 ,向量b 1,0, 3 ,则向量 a在向量b 上的投影向量为( )
B.“ PA PC ”与“ PB PD ”
A. 3,0,1 3B. , 0, 3 3 32 2 C. 1,0, 3 D. ,0, C.“ PB CD ”与“PC AB ” 2 2
D.“平面 PAB 平面 PBD ”与“平面 PCD 平面 PBD ”
π5 .若3sin 4cos 5,则 tan
4
( )
10.有 6本不同的书,按下列方式进行分配,其中分配种数正确的是( )
1 1
A. 7 B.7 C. D. A.分给甲、乙、丙三人,每人各 2本,有 15种分法
7 7
B.分给甲、乙、丙三人,一人 4本,另两人各 1本,有 180种分法
6.已知事件 A与事件 B互相独立,且 P(A) 0.2,P(B) 0.7,则 P(AB) ( )
C.分给甲、乙每人各 2本,分给丙、丁每人各 1本,有 180种分法
A.0.06 B.0.14 C.0.24 D.0.56
D.分给甲、乙、丙、丁四人,两人各 2本,另两人各 1本,有 1080种分法
{#{QQABZbQKhEwggCqwAkAtoSBAACASA4gKCRQwwFGVCCEEgQMkQJkOBhGJAWAgasgOQAAMAKEAMQADAQBZAFQAFBAIAB=A}A#}=}#}
11.已知函数 f (x)( x R )是奇函数, f x 2 f x 且 f 1 2, f x 是 f x 的导函数,则 17.如图,在四棱锥 P ABCD中,PA 平面 ABCD,四边形 ABCD是
矩形, PA AD,过棱 PD的中点 E作 EF PC 于点 F ,连接 AF.
( )
(1)证明: PC AF;
A. f 2023 2 B. f x 的一个周期是 4
(2)若CD 2AD 2,求平面 AEF 与平面 PAB所成夹角的正弦值.
C. f x 是偶函数 D. f 1 1
三、填空题
12.已知 (ax 2)(x
2
)5的展开式中的常数项为 240,则a .
x
13.函数 y x2 4x 5 的单调递增区间是 .
18.某学校组织竞赛,有 A,B两类问题可供选择,其中 A问题答对可得 5分,答错 0分,B问题
14.已知函数 f x cos x 1( 0)在区间 0,2π 有且仅有 3个零点,则 的取值范围是 .
答对只可得 3分,但答错有 2分,现小明与小红参加此竞赛,小红答对 2种问题的概率均为 0.5,
四、解答题
小明答对 A,B问题的概率分别为 0.3,0.7
15 a a 2,a n.已知数列 n 满足: 1 n 1 an 2 .
(1)小红一共参与回答了 2题,记 X为小红的累计得分,求 X的分布列
(1)求 an 的通项公式; (2)小明也参与回答了 2道问题,记 Y为小明的累计得分,求该如何选择问题,使得 E[Y]最大.
1 1 1
(2)若bn log2 an ,Tn b b b b b ,求
Tn .
1 2 2 3 nbn 1
1 19.“拐点”又称“反曲点”,是曲线上弯曲方向发生改变的点.设 x 为函数 x 的导数,若 为 x 16.已知点 A(-2,0),B(2,0),动点 M (x, y)满足直线 AM与 BM的斜率之积为 2 ,记 M的轨迹为
曲线 C. 的极值点,则 , 为曲线 y x 的拐点.
(1)求 C的方程,并说明 C是什么曲线; 已知曲线 C: y x3 3x2 1.
(2)若直线 l : y x 3和曲线 C相交于 E,F两点,求 | EF | .
(1)求 C的拐点坐标;
(2)证明:C关于其拐点对称;
(3)设 l为 C在其拐点处的切线,证明:所有平行于 l的直线都与 C有且仅有一个公共点.
{#{QQABZbQKhEwggCqwAkAtoSBAACASA4gKCRQwwFGVCCEEgQMkQJkOBhGJAWAgasgOQAAMAKEAMQADAQBZAFQAFBAIAB=A}A#}=}#}
2023-2024 学年下学期
( 数学 )科试卷
高三年级适应性考试
A. B.
考试时间:120 分钟 满分:150 分
注意:将答案写在答题卡上,写在本试卷上无效。
一、单选题
1.已知集合 A {x | x 2 x 0},则 1与集合A的关系为( ) C. D.
A. 1 A B. 1 A C. 1 A D. 1 A
2.下列各组函数是同一个函数的是( )
8.已知椭圆C的左、右焦点分别为 F1, F2,下顶点为A,直线 AF1交C于另一点 B,△ABF3 2 的内
A y x x. 与 y x2 B. y x 1
2
与 y x 1
x 1
切圆与 BF2相切于点 P.若 BP F1F2 ,则C的离心率为( )
C y x
2 x
. 与 y x D. y 与 y 1
x x 1A B 1 C 2
3
. . .
3 2 3
D.
4
3.已知复数 z满足 (1 i) z i2024 ( i为虚数单位),则 z ( )
二、多选题
1 i 1 i
A. 1 i B.1 i C. D. 9.已知四棱锥 P ABCD的底面 ABCD是正方形,则下列关系能同时成立的是( )
2 2
A.“ AB PB ”与“ PB BD ”
4.已知向量 a 3,0,1 ,向量b 1,0, 3 ,则向量 a在向量b 上的投影向量为( )
B.“ PA PC ”与“ PB PD ”
A. 3,0,1 3B. , 0, 3 3 32 2 C. 1,0, 3 D. ,0, C.“ PB CD ”与“PC AB ” 2 2
D.“平面 PAB 平面 PBD ”与“平面 PCD 平面 PBD ”
π5 .若3sin 4cos 5,则 tan
4
( )
10.有 6本不同的书,按下列方式进行分配,其中分配种数正确的是( )
1 1
A. 7 B.7 C. D. A.分给甲、乙、丙三人,每人各 2本,有 15种分法
7 7
B.分给甲、乙、丙三人,一人 4本,另两人各 1本,有 180种分法
6.已知事件 A与事件 B互相独立,且 P(A) 0.2,P(B) 0.7,则 P(AB) ( )
C.分给甲、乙每人各 2本,分给丙、丁每人各 1本,有 180种分法
A.0.06 B.0.14 C.0.24 D.0.56
D.分给甲、乙、丙、丁四人,两人各 2本,另两人各 1本,有 1080种分法
{#{QQABZbQKhEwggCqwAkAtoSBAACASA4gKCRQwwFGVCCEEgQMkQJkOBhGJAWAgasgOQAAMAKEAMQADAQBZAFQAFBAIAB=A}A#}=}#}
11.已知函数 f (x)( x R )是奇函数, f x 2 f x 且 f 1 2, f x 是 f x 的导函数,则 17.如图,在四棱锥 P ABCD中,PA 平面 ABCD,四边形 ABCD是
矩形, PA AD,过棱 PD的中点 E作 EF PC 于点 F ,连接 AF.
( )
(1)证明: PC AF;
A. f 2023 2 B. f x 的一个周期是 4
(2)若CD 2AD 2,求平面 AEF 与平面 PAB所成夹角的正弦值.
C. f x 是偶函数 D. f 1 1
三、填空题
12.已知 (ax 2)(x
2
)5的展开式中的常数项为 240,则a .
x
13.函数 y x2 4x 5 的单调递增区间是 .
18.某学校组织竞赛,有 A,B两类问题可供选择,其中 A问题答对可得 5分,答错 0分,B问题
14.已知函数 f x cos x 1( 0)在区间 0,2π 有且仅有 3个零点,则 的取值范围是 .
答对只可得 3分,但答错有 2分,现小明与小红参加此竞赛,小红答对 2种问题的概率均为 0.5,
四、解答题
小明答对 A,B问题的概率分别为 0.3,0.7
15 a a 2,a n.已知数列 n 满足: 1 n 1 an 2 .
(1)小红一共参与回答了 2题,记 X为小红的累计得分,求 X的分布列
(1)求 an 的通项公式; (2)小明也参与回答了 2道问题,记 Y为小明的累计得分,求该如何选择问题,使得 E[Y]最大.
1 1 1
(2)若bn log2 an ,Tn b b b b b ,求
Tn .
1 2 2 3 nbn 1
1 19.“拐点”又称“反曲点”,是曲线上弯曲方向发生改变的点.设 x 为函数 x 的导数,若 为 x 16.已知点 A(-2,0),B(2,0),动点 M (x, y)满足直线 AM与 BM的斜率之积为 2 ,记 M的轨迹为
曲线 C. 的极值点,则 , 为曲线 y x 的拐点.
(1)求 C的方程,并说明 C是什么曲线; 已知曲线 C: y x3 3x2 1.
(2)若直线 l : y x 3和曲线 C相交于 E,F两点,求 | EF | .
(1)求 C的拐点坐标;
(2)证明:C关于其拐点对称;
(3)设 l为 C在其拐点处的切线,证明:所有平行于 l的直线都与 C有且仅有一个公共点.
{#{QQABZbQKhEwggCqwAkAtoSBAACASA4gKCRQwwFGVCCEEgQMkQJkOBhGJAWAgasgOQAAMAKEAMQADAQBZAFQAFBAIAB=A}A#}=}#}
同课章节目录
