2024年成都中考数学压轴大题预测精选(pdf版含答案)
文档属性
| 名称 | 2024年成都中考数学压轴大题预测精选(pdf版含答案) |
|
|
| 格式 | |||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 00:00:00 | ||
图片预览




文档简介
2024成都中考数学压轴大题预测精选及答案解析
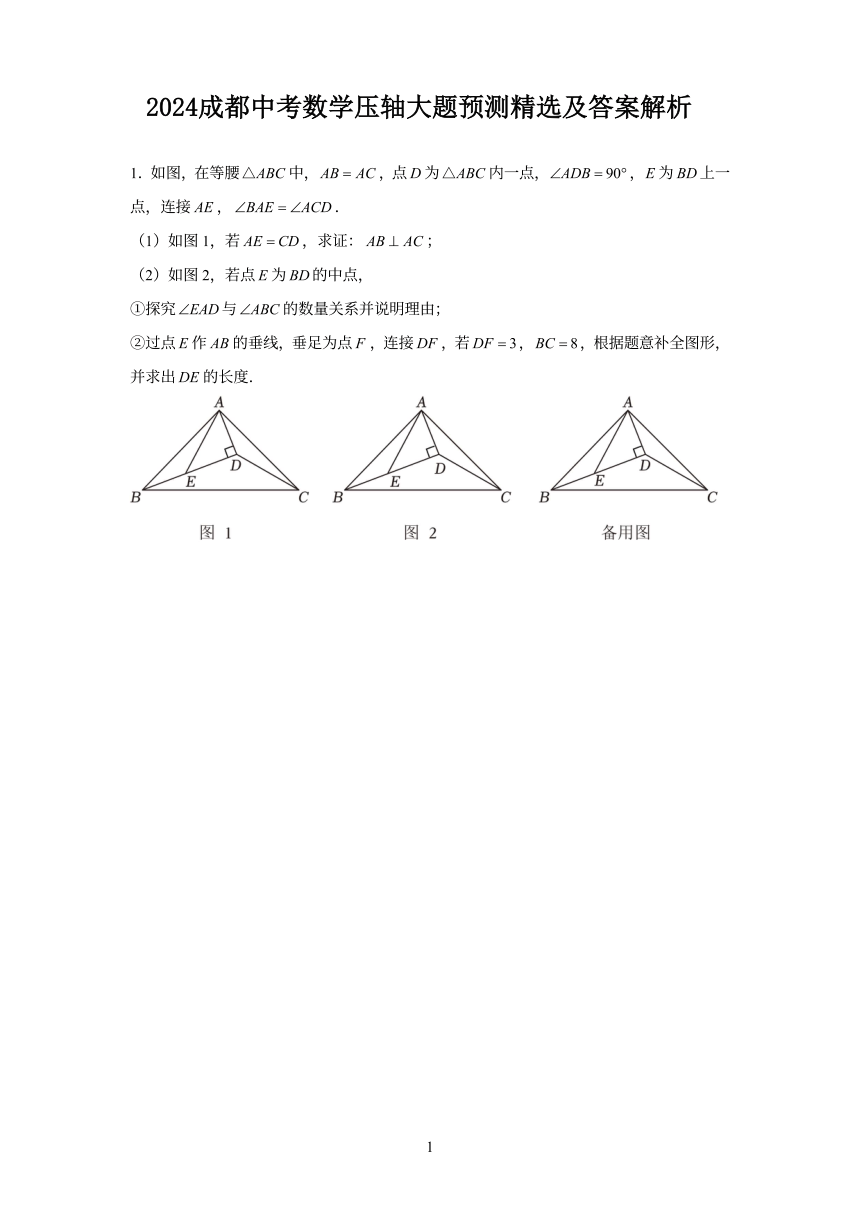
1.如图,在等腰△ABC中,AB=AC,点D为△ABC内一点,∠ADB=90°,E为BD上一
点,连接AE,∠BAE=∠ACD
(1)如图1,若AE=CD,求证:AB⊥AC;
(2)如图2,若点E为BD的中点,
①探究∠EAD与∠ABC的数量关系并说明理由;
②过点E作AB的垂线,垂足为点F,连接DF,若DF=3,BC=8,根据题意补全图形,
并求出DE的长度
D
D
D
E
E
B
B
图1
图2
备用图
2.如图1,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴分别交于A、B两点,与y
轴交于点C,连接AC、BC,其中A(-2,0),C(0,6)
(1)求抛物线的解析式;
(2)点P是直线BC上万抛物线上一点,过点P作PE//y轴交BC于点E,作PF∥x轴交
BC于点F,求CF+BE的最小值,及此时点P的坐标;
(3)如图2,x轴上有一卢Q(-1,0),将抛物线向x轴正万向平移,使得抛物线恰好经过点
Q,得到新抛物线y,卢D是新抛物线y与原抛物线的交点,点E是直线BC上一动点,连
接DQ,当△DQE是以DQ为腰的等腰三角形时,直接写出所有符合条件的点E的坐标
2
y
C
C
图1
图2
2
3.如图①,点D为△ABC上万一动点,且∠BDC=60°,
(I)在BD左例构造△BDE∽△BCA,连接AE,请证明△BAE∽△BCD;
(2)如图②,在BD左例构造△BDE∽△BCA,在CD右例构造△CDF∽△CBA,连接AF,
AE,求正:四边形AFDE是平行四边形;
(3)如图③,当△ABC满足∠A=150°,AB=23,AC=2.运用(2)中的构造图形的万
走画出四边形AFDE;
(I)求证:四边形AFDE是拒形;
(Ⅱ)直接写出在点D运动过程中线段EF的最大值
D
E
B
B
C B
图①
图②
图③
3
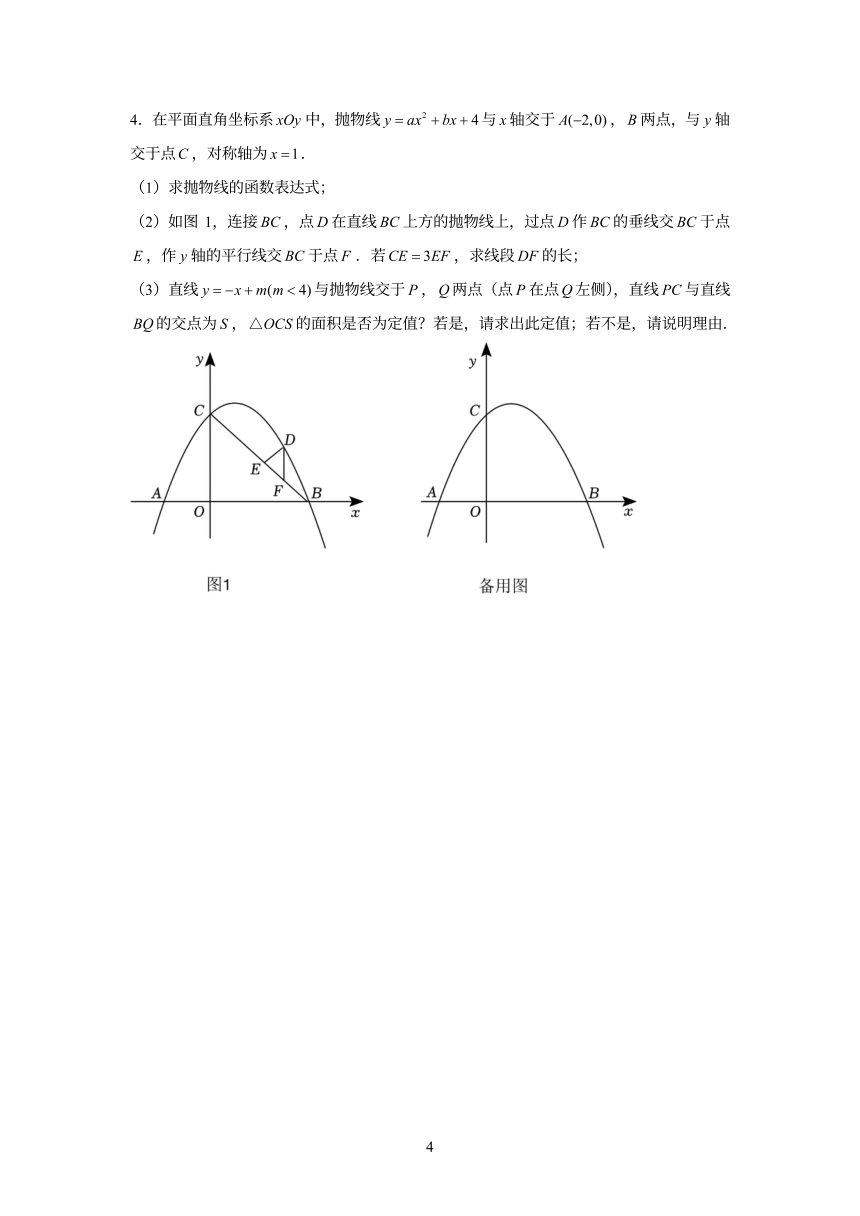
4.在平面直角坐标系xOy中,抛物线y=ax2+br+4与x轴交于A(-2,0),B两点,与y轴
交于点C,对称轴为x=1
(1)求抛物线的函数表达式;
(2)如 1,连接BC,点D在直线BC上万的抛物线上,过点D作BC的垂线交BC于点
E,作y轴的平行线交BC于点F,若CE=3EF,求线段DF的长;
(3)直线y=-x+m(m<4)与抛物线交于P,Q历点(点P在点Q左侧),直线PC与直线
BQ的交点为S,△OCS的面积是否为定值?若是,请末出此定值;若不是,请说明理由,
y
C
D
E
F
B
A
B
图1
备用图
1.如图,在等腰△ABC中,AB=AC,点D为△ABC内一点,∠ADB=90°,E为BD上一
点,连接AE,∠BAE=∠ACD
(1)如图1,若AE=CD,求证:AB⊥AC;
(2)如图2,若点E为BD的中点,
①探究∠EAD与∠ABC的数量关系并说明理由;
②过点E作AB的垂线,垂足为点F,连接DF,若DF=3,BC=8,根据题意补全图形,
并求出DE的长度
D
D
D
E
E
B
B
图1
图2
备用图
2.如图1,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴分别交于A、B两点,与y
轴交于点C,连接AC、BC,其中A(-2,0),C(0,6)
(1)求抛物线的解析式;
(2)点P是直线BC上万抛物线上一点,过点P作PE//y轴交BC于点E,作PF∥x轴交
BC于点F,求CF+BE的最小值,及此时点P的坐标;
(3)如图2,x轴上有一卢Q(-1,0),将抛物线向x轴正万向平移,使得抛物线恰好经过点
Q,得到新抛物线y,卢D是新抛物线y与原抛物线的交点,点E是直线BC上一动点,连
接DQ,当△DQE是以DQ为腰的等腰三角形时,直接写出所有符合条件的点E的坐标
2
y
C
C
图1
图2
2
3.如图①,点D为△ABC上万一动点,且∠BDC=60°,
(I)在BD左例构造△BDE∽△BCA,连接AE,请证明△BAE∽△BCD;
(2)如图②,在BD左例构造△BDE∽△BCA,在CD右例构造△CDF∽△CBA,连接AF,
AE,求正:四边形AFDE是平行四边形;
(3)如图③,当△ABC满足∠A=150°,AB=23,AC=2.运用(2)中的构造图形的万
走画出四边形AFDE;
(I)求证:四边形AFDE是拒形;
(Ⅱ)直接写出在点D运动过程中线段EF的最大值
D
E
B
B
C B
图①
图②
图③
3
4.在平面直角坐标系xOy中,抛物线y=ax2+br+4与x轴交于A(-2,0),B两点,与y轴
交于点C,对称轴为x=1
(1)求抛物线的函数表达式;
(2)如 1,连接BC,点D在直线BC上万的抛物线上,过点D作BC的垂线交BC于点
E,作y轴的平行线交BC于点F,若CE=3EF,求线段DF的长;
(3)直线y=-x+m(m<4)与抛物线交于P,Q历点(点P在点Q左侧),直线PC与直线
BQ的交点为S,△OCS的面积是否为定值?若是,请末出此定值;若不是,请说明理由,
y
C
D
E
F
B
A
B
图1
备用图
同课章节目录
