沪科版八年级数学上册第12章 一次函数 全章复习基础试题 (含解析)
文档属性
| 名称 | 沪科版八年级数学上册第12章 一次函数 全章复习基础试题 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 760.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 00:00:00 | ||
图片预览

文档简介
第12章 《一次函数》全章复习(基础篇)
一、单选题
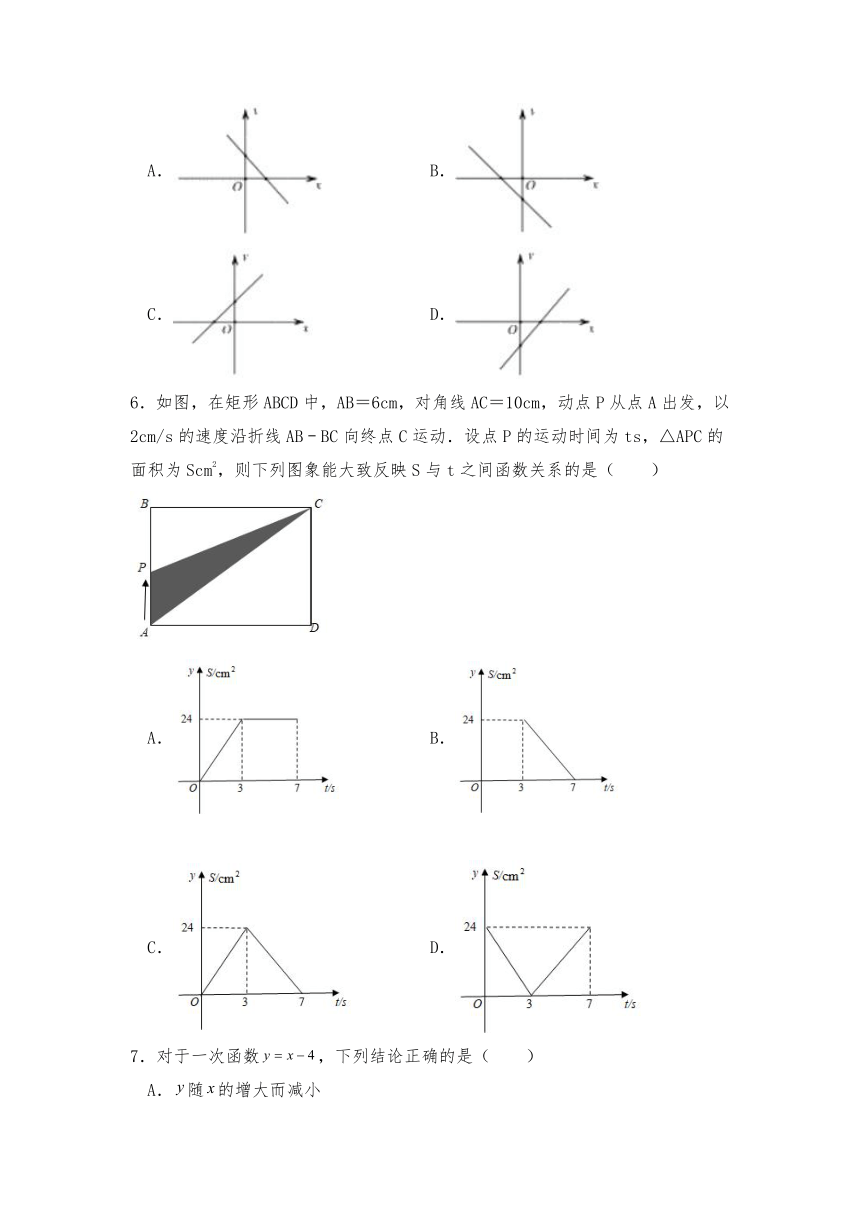
1.下列图象中,表示y是x的函数的个数有( )
A.1个 B.2个 C.3个 D.4个
2.下列等式中,是的函数有( )个.
A.1 B.2 C.3 D.4
3.函数中,自变量x的取值范围是( )
A. B.且 C. D.且
4.甲、乙两地相距180km,一辆货车和一辆小汽车同时从甲地出发,各自匀速向乙地行驶,货车的速度为60千米/小时,小汽车的速度为90千米/小时.小汽车到达乙地后,立即按原速沿原路返回甲地.则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )
A. B.
C. D.
5.正比例函数y=kx的图象经过一、三象限,则一次函数y=﹣kx+k的图象大致是( )
A. B.
C. D.
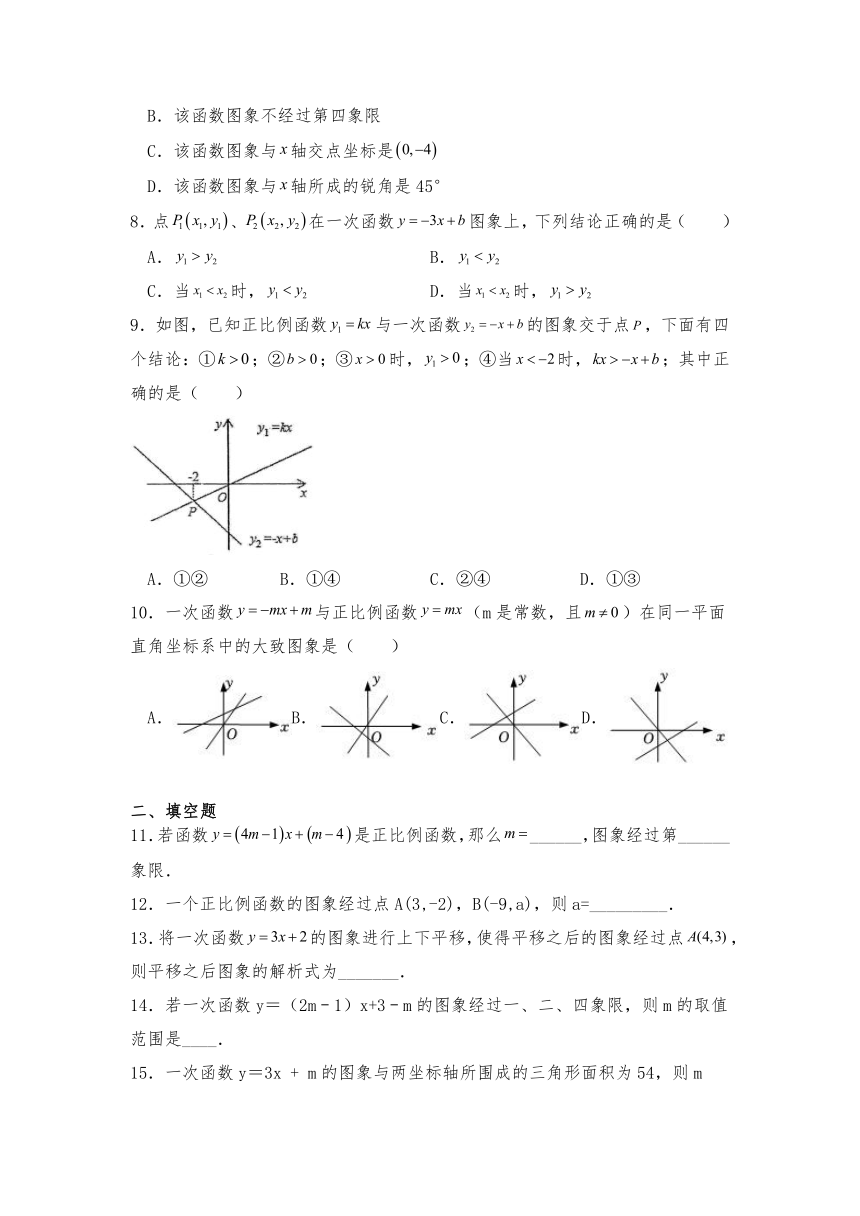
6.如图,在矩形ABCD中,AB=6cm,对角线AC=10cm,动点P从点A出发,以2cm/s的速度沿折线AB﹣BC向终点C运动.设点P的运动时间为ts,△APC的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
7.对于一次函数,下列结论正确的是( )
A.随的增大而减小
B.该函数图象不经过第四象限
C.该函数图象与轴交点坐标是
D.该函数图象与轴所成的锐角是45°
8.点、在一次函数图象上,下列结论正确的是( )
A. B.
C.当时, D.当时,
9.如图,已知正比例函数与一次函数的图象交于点,下面有四个结论:①;②;③时,;④当时,;其中正确的是( )
A.①② B.①④ C.②④ D.①③
10.一次函数与正比例函数(m是常数,且)在同一平面直角坐标系中的大致图象是( )
A.B.C.D.
二、填空题
11.若函数是正比例函数,那么______,图象经过第______象限.
12.一个正比例函数的图象经过点A(3,-2),B(-9,a),则a=_________.
13.将一次函数的图象进行上下平移,使得平移之后的图象经过点,则平移之后图象的解析式为_______.
14.若一次函数y=(2m﹣1)x+3﹣m的图象经过一、二、四象限,则m的取值范围是____.
15.一次函数y=3x + m的图象与两坐标轴所围成的三角形面积为54,则m =___________ .
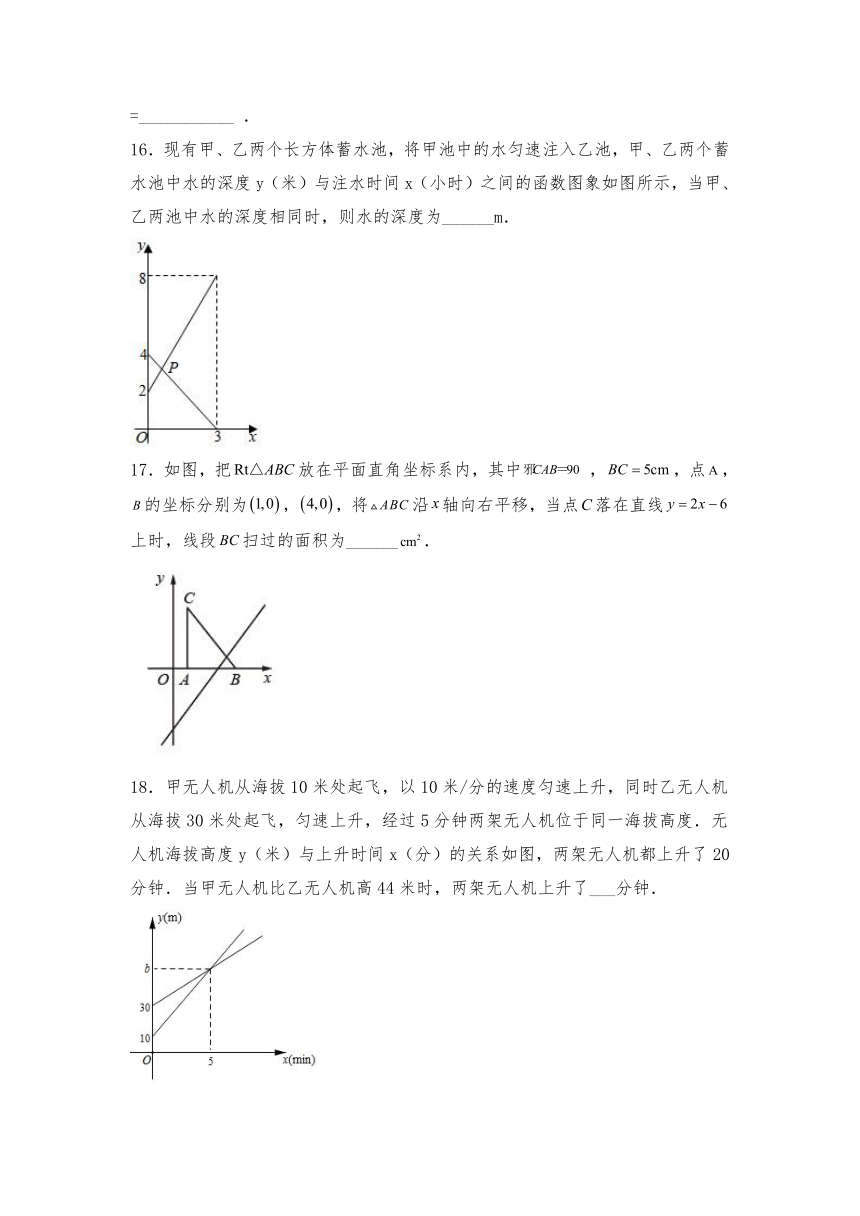
16.现有甲、乙两个长方体蓄水池,将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(小时)之间的函数图象如图所示,当甲、乙两池中水的深度相同时,则水的深度为______m.
17.如图,把放在平面直角坐标系内,其中,,点,的坐标分别为,,将沿轴向右平移,当点落在直线上时,线段扫过的面积为______.
18.甲无人机从海拔10米处起飞,以10米/分的速度匀速上升,同时乙无人机从海拔30米处起飞,匀速上升,经过5分钟两架无人机位于同一海拔高度.无人机海拔高度y(米)与上升时间x(分)的关系如图,两架无人机都上升了20分钟.当甲无人机比乙无人机高44米时,两架无人机上升了___分钟.
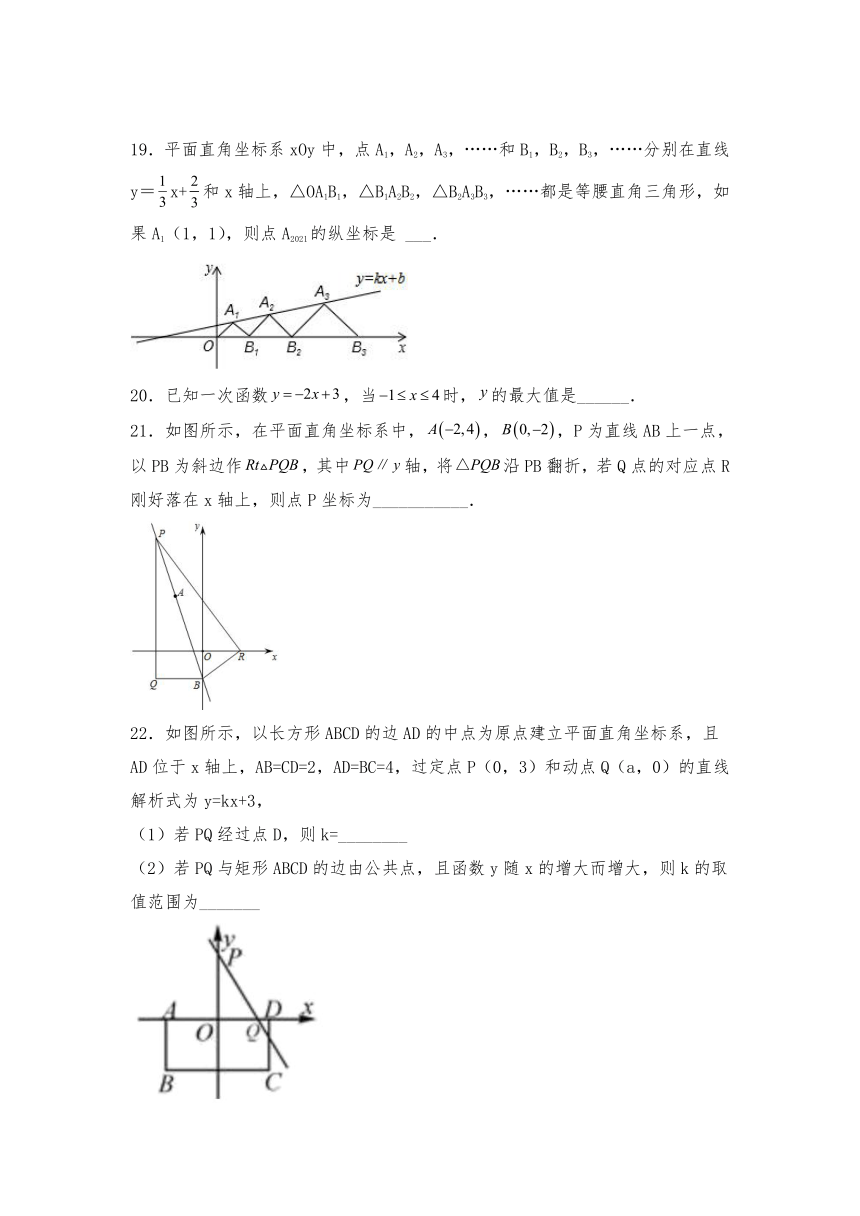
19.平面直角坐标系xOy中,点A1,A2,A3,……和B1,B2,B3,……分别在直线y=x+和x轴上,△OA1B1,△B1A2B2,△B2A3B3,……都是等腰直角三角形,如果A1(1,1),则点A2021的纵坐标是 ___.
20.已知一次函数,当时,的最大值是______.
21.如图所示,在平面直角坐标系中,,,P为直线AB上一点,以PB为斜边作,其中轴,将沿PB翻折,若Q点的对应点R刚好落在x轴上,则点P坐标为___________.
22.如图所示,以长方形ABCD的边AD的中点为原点建立平面直角坐标系,且AD位于x轴上,AB=CD=2,AD=BC=4,过定点P(0,3)和动点Q(a,0)的直线解析式为y=kx+3,
(1)若PQ经过点D,则k=________
(2)若PQ与矩形ABCD的边由公共点,且函数y随x的增大而增大,则k的取值范围为_______
三、解答题
23.已知与x成正比例,当时,.
(1)求出y与x的函数关系式;
(2)点P1(m,y1)、P2(m+1,y2)在(1)中函数的图象上,比较y1与y2的大小.
24.如图,已知直线y=ax+b与直线y=cx+d相交于点P(,).
(1)求2a+3b的值;
(2)观察图象,直接写出ax+b<cx+d的解集.
25.目前,全国各地都在积极开展新冠肺炎疫苗接种工作,某生物公司接到批量生产疫苗任务,要求5天内加工完成22万支疫苗,该公司安排甲,乙两车间共同完成加工任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止,设甲,乙两车间各自生产疫苗(万支)与甲车间加工时间(天)之间的关系如图1所示;未生产疫苗(万支)与甲车间加工时间(天)之间的关系如图2所示,请结合图象回答下列问题:
(1)甲车间每天生产疫苗______万支,______.
(2)求乙车间维修设备后生产疫苗数量(万支)与(天)之间的函数关系式,并写出自变量的取值范围.
(3)若5.5万支疫苗恰好装满一辆货车,那么加工多少天装满第一辆货车?再加工多少天恰好装满第二辆货车?(直接写出答案即可).
26.如图,平面直角坐标系中,点O为坐标原点,直线AB分别与x轴、y轴交于点A(4,0),B(0,4).
(1)求直线AB的函数表达式;
(2)若点P为此函数图像上的一点,且AOP是以AO为腰的等腰三角形,求此时P点的坐标.
答案
一、单选题
1.B
【分析】
根据函数的定义:设在某变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一确定的值与它对应,那么就称y是x的函数,x叫做自变量,据此判断即可.
【详解】
解:属于函数的有
故y是x的函数的个数有2个,
故选:B.
2.C
【分析】
根据函数的定义:在一个变化过程中,如果两个变量x和y,对于x的每一个确定的值,y都有唯一的值与值对应,那么就称y是x的函数,由此进行判断即可.
【详解】
解:满足函数的定义,符合题意;
当时,即不符合题意;
满足函数的定义,符合题意;
,当时,即不符合题意;
故符合y是x的函数的有三个,
3.B
【分析】
根据被开方数大于等于0,分母不等于0列式进行计算即可得解.
【详解】
解:根据题意得,x-2≥0且x 3≠0,
解得且.
故选:B.
4.C
【分析】
根据出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米;经过三小时,货车到达乙地距离变为零,故而得出答案.
【详解】
解:由题意得出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米,经过三小时,货车到达乙地距离变为零,故C符合题意,
故选:C.
5.A
【分析】
由正比例函数的图象经过一、三象限,可以知道,由此,从而得到一次函数图象情况.
【详解】
解:∵正比例函数y=kx的图象经过一、三象限
∴
∴
∴一次函数的图象经过一、二、四象限
故选:A
6.C
7.D
【分析】
由题意根据一次函数的性质以及函数图象与坐标轴的交点的求法逐项进行判断即可.
【详解】
解:A. ,随的增大而增大,选项错误;
B. ,该函数图象经过第一、三、四象限,不经过第二象限,选项错误;
C. 该函数图象与轴交点坐标是,选项错误;
D. 该函数图象与轴正方向所成的锐角是45°,选项正确.
故选:D.
8.D
【分析】
根据一次函数的增减性即可得.
【详解】
解:一次函数的一次项系数为,
随的增大而减小,
点、在此函数的图象上,
当时,,
故选:D.
9.D
【分析】
根据正比例函数和一次函数的性质判断即可.
【详解】
解:∵直线经过第一、三象限,
∴k>0,故①正确;
∵与y轴交点在负半轴,
∴b<0,故②错误;
∵正比例函数经过原点,且y随x的增大而增大,
∴当x>0时,y1>0;故③正确;
当x<-2时,正比例函数在一次函数图象的下方,即kx<,故④错误.
故选:D.
10.D
【分析】
根据一次函数的图象性质和正比例函数的图象性质分别判断即可;
【详解】
由一次函数图象可得,,则,与正比例函数图象不相符,故A不正确;
由一次函数图像可得,,则,正比例函数图象正确,但一次函数图像与y轴应交于正半轴,交点位置不正确,故B不正确;
由一次函数图像可得,,则,正比例函数图象正确,但一次函数图像与y轴应交于负半轴,交点位置不正确,故C不正确;
由一次函数图像可得,,则,与正比例函数图象相符,故D正确;
故选D.
二、填空题
11.4 一、三
【分析】
根据题意可得,求出,再判定的符号即可.
【详解】
解:函数是正比例函数,
∴,解得,
∴
∴图象过第一、三象限,
故答案为;一、三
12.6
【分析】
根据待定系数法求出正比例函数解析式,然后将点B(-9,a)代入解析式即可得出答案.
【详解】
解:∵正比例函数的图象经过点A(3,-2),B(-9,a),
∴设正比例函数的解析式为:,
则,解得:,
∴正比例函数的解析式为:,
∴,
故答案为:.
13.
【分析】
根据一次函数图像平移规律:上加下减,左加右减,进行解答即可.
【详解】
解:设一次函数平移后的解析式为:,
∵移之后的图象经过点,
∴,
解得:,
∴平移之后图象的解析式为,
故答案为:.
14.m<
【分析】
根据一次函数的性质可知(2m﹣1)<0,3﹣m>0,即可求出m的取值范围.
【详解】
解:∵y=(2m﹣1)x+3﹣m的图象经过 一、二、四象限
∴,
解得m<,
∴m的取值范围是m<.
故答案为:m<.
15.±18
【分析】
分别令x=0求出y的值,再令y=0求出x的值,由三角形的面积公式求出m的值即可.
【详解】
解:令x=0,则y=m,令y=0,则x=-,
∵一次函数y=mx+2的图象与两坐标轴围成的三角形的面积为54,
∴×||×|-|=54,解得m=±18.
故答案为:±18.
16.3.2
【分析】
根据函数图象中的数据可以求得相应的函数解析式;联立两个函数解析式,即可求交点P的坐标,点P的纵坐标即为所求.
【详解】
解:设y1为甲池中的水深度与注水时间x之间的函数表达式是y1=k1x+b1,
∴,
解得:,
即y1=-x+4 (0≤x≤3),
设y2乙池中的水深度与注水时间x之间的函数表达式是y2=k2x+b2,
∴,
解得,
即y2=2x+2 (0≤x≤3);
令y1=y2,则-x+4=2x+2,
解得:x=,
y=2×+2=,
∴P(,),
∴当甲、乙两池中水的深度相同时,则水的深度为米,即3.2米.
故答案为:3.2.
17.16
【分析】
先根据勾股定理求出C点的坐标,得到C1的纵坐标为4,与直线 相交,可得C1坐标,由此推出CC1距离,再求出四边形BCC1B1的面积即可.
【详解】
解:∵A(1,0),B(4,0)
∴AB=3
∵,∠CAB=90°,
∴
∴C(1,4),
∴C1的纵坐标为4,
∴把代入解得,
∴CC1=4,
∴,
故答案为:16.
18.16
【分析】
由题意求出两架无人机的函数表达式,列出方程(10x+10)﹣(6x+30)=44,即可求解.
【详解】
解:甲无人机拔高度y(米)与上升时间x(分)的关系式为 y=10x+10,
把x=5代入,得,y=10+10×5=60,
设乙无人机的函数的表达式为y=kx+t,
将(0,30)、(5,60)代入得,解得,
乙无人机的函数表达式为y=6x+30;
(10x+10)﹣(6x+30)=44,
解得,x=16,
故答案为:16
19.22020
【分析】
利用待定系数法可得A1、A2、A3的坐标,进而得出各点的坐标的规律.
【详解】
解:∵A1(1,1),
∵△OA1B1为等腰直角三角形
∴点B1 (0,2),
∵直线OA1,B1A2,B2A3互相平行,而已知直线OA1的解析式为:
∴直线的解析式为:,
∴设A2(2+a,a),则a=(a+2)+,
解得a=2,
∴A2(4,2),
∵△B1A2B2为等腰直角三角形
∴点B2 (0,6),
直线的解析式为:
设A3(6+b,b),则有b=(6+b)+,
解得b=4,
∴A3(10,4),
由此发现点An的纵坐标为2n-1,
即点A2021的纵坐标是22020,
故答案为:22020.
20.5
【分析】
根据一次函数的增减性确定.
【详解】
∵一次函数中,k= -2<0,
∴y随x的增大而减小,
∵,
∴当x=-1时,函数y有最大值,
此时y=2+3=5,
故答案为:5.
21.
【分析】
根据,,求出直线AB的表达式,设出点P和点Q的坐标,根据折叠的性质表示出BR和PR,最后根据勾股定理列方程求解即可.
【详解】
如图,设PQ交x轴于M,
∵,,
∴设直线AB的解析式为y=kx+b,
∴,
解得:,
∴直线AB的解析式为y=-3x-2,
设P(m,-3m-2),Q(m,-2),M(m,0),
∴PQ=-3m-2-(-2)=-3m,BQ=-m,
∵将沿PB翻折,若Q点的对应点R刚好落在x轴上,
∴BR=BQ=-m,PR=PQ=-3m,
∴OR==,
∴MR=OM+OR=-m,
在Rt△PMR中,PR2=PM2+MR2,
∴(-3m)2=(-3m-2)2+(-m)2,
∴9m2=9m2+12m+4+m2-4-2m+m2,
整理得:2m2+12m-2m=m(2m-2+12)=0,
∵m≠0,
∴2m-2+12=0,
解得:,
∴-3m-2=8,
∴点P坐标为(,8).
22.- k≥
【分析】
(1)根据坐标系,矩形的性质,确定点D(2,0),代入解析式求解即可;
(2)函数y随x的增大而增大,故k大于零,根据坐标系,矩形的性质,确定点A(-2,0),代入解析式求解即可.
【详解】
(1)∵长方形ABCD的边AD的中点为原点建立平面直角坐标系,且AD位于x轴上,AB=CD=2,AD=BC=4,
∴A(-2,0),D(2,0),
∵过定点P(0,3)和动点Q(a,0)的直线解析式为y=kx+3,
∴2k+3=0,
解得k=-,
故答案为:-;
(2)∵函数y随x的增大而增大,
∴k>0,
∵PQ与矩形ABCD的边由公共点,
∴经过点A时,是直线k的最小值,
∴-2k+3=0,
解得k=,
∴k≥,
故答案为:k≥.
三、解答题
23.
(1)与x成正比例,
设
当时,.
解得
(2)点P1(m,y1)、P2(m+1,y2)在的图象上,
随的增大而减小,
24.
解:(1)把P(,)代入y=ax+b得,
,
去分母得,;
(2)根据图象可知,在P(,)左侧,ax+b<cx+d.
所以,ax+b<cx+d的解集为.
25.
解:(1)由图1可得,
甲车间每天生产疫苗:(22-12)÷5=2(万支),
由图2可得,
a=22-18.5-2×1=22-18.5-2=1.5,
故答案为:2,1.5;
(2)当乙车间维修设备后,即2<x≤5时,设y与x的函数关系式为y=kx+b,
,
解得,
即当2<x≤5时,y与x的函数关系式为y=3.5x-5.5;
(3)由图2可得,
当x=2时,生产的疫苗有22-16.5=5.5(万支),
当2≤x≤5时,每天生产的疫苗有:16.5÷(5-2)=5.5(万支),
∴加工两天装满第一辆货车,再过1天装满第二辆货车.
26.解:(1)设,将A(4,0),B(0,4)代入得
,解得,
即;
(2)设,由题意可得:
AOP是以AO为腰的等腰三角形
当时,则点与点重合,即
当时,,解得
则或
故点P的坐标为或或
一、单选题
1.下列图象中,表示y是x的函数的个数有( )
A.1个 B.2个 C.3个 D.4个
2.下列等式中,是的函数有( )个.
A.1 B.2 C.3 D.4
3.函数中,自变量x的取值范围是( )
A. B.且 C. D.且
4.甲、乙两地相距180km,一辆货车和一辆小汽车同时从甲地出发,各自匀速向乙地行驶,货车的速度为60千米/小时,小汽车的速度为90千米/小时.小汽车到达乙地后,立即按原速沿原路返回甲地.则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )
A. B.
C. D.
5.正比例函数y=kx的图象经过一、三象限,则一次函数y=﹣kx+k的图象大致是( )
A. B.
C. D.
6.如图,在矩形ABCD中,AB=6cm,对角线AC=10cm,动点P从点A出发,以2cm/s的速度沿折线AB﹣BC向终点C运动.设点P的运动时间为ts,△APC的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
7.对于一次函数,下列结论正确的是( )
A.随的增大而减小
B.该函数图象不经过第四象限
C.该函数图象与轴交点坐标是
D.该函数图象与轴所成的锐角是45°
8.点、在一次函数图象上,下列结论正确的是( )
A. B.
C.当时, D.当时,
9.如图,已知正比例函数与一次函数的图象交于点,下面有四个结论:①;②;③时,;④当时,;其中正确的是( )
A.①② B.①④ C.②④ D.①③
10.一次函数与正比例函数(m是常数,且)在同一平面直角坐标系中的大致图象是( )
A.B.C.D.
二、填空题
11.若函数是正比例函数,那么______,图象经过第______象限.
12.一个正比例函数的图象经过点A(3,-2),B(-9,a),则a=_________.
13.将一次函数的图象进行上下平移,使得平移之后的图象经过点,则平移之后图象的解析式为_______.
14.若一次函数y=(2m﹣1)x+3﹣m的图象经过一、二、四象限,则m的取值范围是____.
15.一次函数y=3x + m的图象与两坐标轴所围成的三角形面积为54,则m =___________ .
16.现有甲、乙两个长方体蓄水池,将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(小时)之间的函数图象如图所示,当甲、乙两池中水的深度相同时,则水的深度为______m.
17.如图,把放在平面直角坐标系内,其中,,点,的坐标分别为,,将沿轴向右平移,当点落在直线上时,线段扫过的面积为______.
18.甲无人机从海拔10米处起飞,以10米/分的速度匀速上升,同时乙无人机从海拔30米处起飞,匀速上升,经过5分钟两架无人机位于同一海拔高度.无人机海拔高度y(米)与上升时间x(分)的关系如图,两架无人机都上升了20分钟.当甲无人机比乙无人机高44米时,两架无人机上升了___分钟.
19.平面直角坐标系xOy中,点A1,A2,A3,……和B1,B2,B3,……分别在直线y=x+和x轴上,△OA1B1,△B1A2B2,△B2A3B3,……都是等腰直角三角形,如果A1(1,1),则点A2021的纵坐标是 ___.
20.已知一次函数,当时,的最大值是______.
21.如图所示,在平面直角坐标系中,,,P为直线AB上一点,以PB为斜边作,其中轴,将沿PB翻折,若Q点的对应点R刚好落在x轴上,则点P坐标为___________.
22.如图所示,以长方形ABCD的边AD的中点为原点建立平面直角坐标系,且AD位于x轴上,AB=CD=2,AD=BC=4,过定点P(0,3)和动点Q(a,0)的直线解析式为y=kx+3,
(1)若PQ经过点D,则k=________
(2)若PQ与矩形ABCD的边由公共点,且函数y随x的增大而增大,则k的取值范围为_______
三、解答题
23.已知与x成正比例,当时,.
(1)求出y与x的函数关系式;
(2)点P1(m,y1)、P2(m+1,y2)在(1)中函数的图象上,比较y1与y2的大小.
24.如图,已知直线y=ax+b与直线y=cx+d相交于点P(,).
(1)求2a+3b的值;
(2)观察图象,直接写出ax+b<cx+d的解集.
25.目前,全国各地都在积极开展新冠肺炎疫苗接种工作,某生物公司接到批量生产疫苗任务,要求5天内加工完成22万支疫苗,该公司安排甲,乙两车间共同完成加工任务,乙车间加工过程中停工一段时间维修设备,然后提高效率继续加工,直到与甲车间同时完成加工任务为止,设甲,乙两车间各自生产疫苗(万支)与甲车间加工时间(天)之间的关系如图1所示;未生产疫苗(万支)与甲车间加工时间(天)之间的关系如图2所示,请结合图象回答下列问题:
(1)甲车间每天生产疫苗______万支,______.
(2)求乙车间维修设备后生产疫苗数量(万支)与(天)之间的函数关系式,并写出自变量的取值范围.
(3)若5.5万支疫苗恰好装满一辆货车,那么加工多少天装满第一辆货车?再加工多少天恰好装满第二辆货车?(直接写出答案即可).
26.如图,平面直角坐标系中,点O为坐标原点,直线AB分别与x轴、y轴交于点A(4,0),B(0,4).
(1)求直线AB的函数表达式;
(2)若点P为此函数图像上的一点,且AOP是以AO为腰的等腰三角形,求此时P点的坐标.
答案
一、单选题
1.B
【分析】
根据函数的定义:设在某变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一确定的值与它对应,那么就称y是x的函数,x叫做自变量,据此判断即可.
【详解】
解:属于函数的有
故y是x的函数的个数有2个,
故选:B.
2.C
【分析】
根据函数的定义:在一个变化过程中,如果两个变量x和y,对于x的每一个确定的值,y都有唯一的值与值对应,那么就称y是x的函数,由此进行判断即可.
【详解】
解:满足函数的定义,符合题意;
当时,即不符合题意;
满足函数的定义,符合题意;
,当时,即不符合题意;
故符合y是x的函数的有三个,
3.B
【分析】
根据被开方数大于等于0,分母不等于0列式进行计算即可得解.
【详解】
解:根据题意得,x-2≥0且x 3≠0,
解得且.
故选:B.
4.C
【分析】
根据出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米;经过三小时,货车到达乙地距离变为零,故而得出答案.
【详解】
解:由题意得出发前都距离乙地180千米,出发两小时小汽车到达乙地距离变为零,再经过两小时小汽车又返回甲地距离又为180千米,经过三小时,货车到达乙地距离变为零,故C符合题意,
故选:C.
5.A
【分析】
由正比例函数的图象经过一、三象限,可以知道,由此,从而得到一次函数图象情况.
【详解】
解:∵正比例函数y=kx的图象经过一、三象限
∴
∴
∴一次函数的图象经过一、二、四象限
故选:A
6.C
7.D
【分析】
由题意根据一次函数的性质以及函数图象与坐标轴的交点的求法逐项进行判断即可.
【详解】
解:A. ,随的增大而增大,选项错误;
B. ,该函数图象经过第一、三、四象限,不经过第二象限,选项错误;
C. 该函数图象与轴交点坐标是,选项错误;
D. 该函数图象与轴正方向所成的锐角是45°,选项正确.
故选:D.
8.D
【分析】
根据一次函数的增减性即可得.
【详解】
解:一次函数的一次项系数为,
随的增大而减小,
点、在此函数的图象上,
当时,,
故选:D.
9.D
【分析】
根据正比例函数和一次函数的性质判断即可.
【详解】
解:∵直线经过第一、三象限,
∴k>0,故①正确;
∵与y轴交点在负半轴,
∴b<0,故②错误;
∵正比例函数经过原点,且y随x的增大而增大,
∴当x>0时,y1>0;故③正确;
当x<-2时,正比例函数在一次函数图象的下方,即kx<,故④错误.
故选:D.
10.D
【分析】
根据一次函数的图象性质和正比例函数的图象性质分别判断即可;
【详解】
由一次函数图象可得,,则,与正比例函数图象不相符,故A不正确;
由一次函数图像可得,,则,正比例函数图象正确,但一次函数图像与y轴应交于正半轴,交点位置不正确,故B不正确;
由一次函数图像可得,,则,正比例函数图象正确,但一次函数图像与y轴应交于负半轴,交点位置不正确,故C不正确;
由一次函数图像可得,,则,与正比例函数图象相符,故D正确;
故选D.
二、填空题
11.4 一、三
【分析】
根据题意可得,求出,再判定的符号即可.
【详解】
解:函数是正比例函数,
∴,解得,
∴
∴图象过第一、三象限,
故答案为;一、三
12.6
【分析】
根据待定系数法求出正比例函数解析式,然后将点B(-9,a)代入解析式即可得出答案.
【详解】
解:∵正比例函数的图象经过点A(3,-2),B(-9,a),
∴设正比例函数的解析式为:,
则,解得:,
∴正比例函数的解析式为:,
∴,
故答案为:.
13.
【分析】
根据一次函数图像平移规律:上加下减,左加右减,进行解答即可.
【详解】
解:设一次函数平移后的解析式为:,
∵移之后的图象经过点,
∴,
解得:,
∴平移之后图象的解析式为,
故答案为:.
14.m<
【分析】
根据一次函数的性质可知(2m﹣1)<0,3﹣m>0,即可求出m的取值范围.
【详解】
解:∵y=(2m﹣1)x+3﹣m的图象经过 一、二、四象限
∴,
解得m<,
∴m的取值范围是m<.
故答案为:m<.
15.±18
【分析】
分别令x=0求出y的值,再令y=0求出x的值,由三角形的面积公式求出m的值即可.
【详解】
解:令x=0,则y=m,令y=0,则x=-,
∵一次函数y=mx+2的图象与两坐标轴围成的三角形的面积为54,
∴×||×|-|=54,解得m=±18.
故答案为:±18.
16.3.2
【分析】
根据函数图象中的数据可以求得相应的函数解析式;联立两个函数解析式,即可求交点P的坐标,点P的纵坐标即为所求.
【详解】
解:设y1为甲池中的水深度与注水时间x之间的函数表达式是y1=k1x+b1,
∴,
解得:,
即y1=-x+4 (0≤x≤3),
设y2乙池中的水深度与注水时间x之间的函数表达式是y2=k2x+b2,
∴,
解得,
即y2=2x+2 (0≤x≤3);
令y1=y2,则-x+4=2x+2,
解得:x=,
y=2×+2=,
∴P(,),
∴当甲、乙两池中水的深度相同时,则水的深度为米,即3.2米.
故答案为:3.2.
17.16
【分析】
先根据勾股定理求出C点的坐标,得到C1的纵坐标为4,与直线 相交,可得C1坐标,由此推出CC1距离,再求出四边形BCC1B1的面积即可.
【详解】
解:∵A(1,0),B(4,0)
∴AB=3
∵,∠CAB=90°,
∴
∴C(1,4),
∴C1的纵坐标为4,
∴把代入解得,
∴CC1=4,
∴,
故答案为:16.
18.16
【分析】
由题意求出两架无人机的函数表达式,列出方程(10x+10)﹣(6x+30)=44,即可求解.
【详解】
解:甲无人机拔高度y(米)与上升时间x(分)的关系式为 y=10x+10,
把x=5代入,得,y=10+10×5=60,
设乙无人机的函数的表达式为y=kx+t,
将(0,30)、(5,60)代入得,解得,
乙无人机的函数表达式为y=6x+30;
(10x+10)﹣(6x+30)=44,
解得,x=16,
故答案为:16
19.22020
【分析】
利用待定系数法可得A1、A2、A3的坐标,进而得出各点的坐标的规律.
【详解】
解:∵A1(1,1),
∵△OA1B1为等腰直角三角形
∴点B1 (0,2),
∵直线OA1,B1A2,B2A3互相平行,而已知直线OA1的解析式为:
∴直线的解析式为:,
∴设A2(2+a,a),则a=(a+2)+,
解得a=2,
∴A2(4,2),
∵△B1A2B2为等腰直角三角形
∴点B2 (0,6),
直线的解析式为:
设A3(6+b,b),则有b=(6+b)+,
解得b=4,
∴A3(10,4),
由此发现点An的纵坐标为2n-1,
即点A2021的纵坐标是22020,
故答案为:22020.
20.5
【分析】
根据一次函数的增减性确定.
【详解】
∵一次函数中,k= -2<0,
∴y随x的增大而减小,
∵,
∴当x=-1时,函数y有最大值,
此时y=2+3=5,
故答案为:5.
21.
【分析】
根据,,求出直线AB的表达式,设出点P和点Q的坐标,根据折叠的性质表示出BR和PR,最后根据勾股定理列方程求解即可.
【详解】
如图,设PQ交x轴于M,
∵,,
∴设直线AB的解析式为y=kx+b,
∴,
解得:,
∴直线AB的解析式为y=-3x-2,
设P(m,-3m-2),Q(m,-2),M(m,0),
∴PQ=-3m-2-(-2)=-3m,BQ=-m,
∵将沿PB翻折,若Q点的对应点R刚好落在x轴上,
∴BR=BQ=-m,PR=PQ=-3m,
∴OR==,
∴MR=OM+OR=-m,
在Rt△PMR中,PR2=PM2+MR2,
∴(-3m)2=(-3m-2)2+(-m)2,
∴9m2=9m2+12m+4+m2-4-2m+m2,
整理得:2m2+12m-2m=m(2m-2+12)=0,
∵m≠0,
∴2m-2+12=0,
解得:,
∴-3m-2=8,
∴点P坐标为(,8).
22.- k≥
【分析】
(1)根据坐标系,矩形的性质,确定点D(2,0),代入解析式求解即可;
(2)函数y随x的增大而增大,故k大于零,根据坐标系,矩形的性质,确定点A(-2,0),代入解析式求解即可.
【详解】
(1)∵长方形ABCD的边AD的中点为原点建立平面直角坐标系,且AD位于x轴上,AB=CD=2,AD=BC=4,
∴A(-2,0),D(2,0),
∵过定点P(0,3)和动点Q(a,0)的直线解析式为y=kx+3,
∴2k+3=0,
解得k=-,
故答案为:-;
(2)∵函数y随x的增大而增大,
∴k>0,
∵PQ与矩形ABCD的边由公共点,
∴经过点A时,是直线k的最小值,
∴-2k+3=0,
解得k=,
∴k≥,
故答案为:k≥.
三、解答题
23.
(1)与x成正比例,
设
当时,.
解得
(2)点P1(m,y1)、P2(m+1,y2)在的图象上,
随的增大而减小,
24.
解:(1)把P(,)代入y=ax+b得,
,
去分母得,;
(2)根据图象可知,在P(,)左侧,ax+b<cx+d.
所以,ax+b<cx+d的解集为.
25.
解:(1)由图1可得,
甲车间每天生产疫苗:(22-12)÷5=2(万支),
由图2可得,
a=22-18.5-2×1=22-18.5-2=1.5,
故答案为:2,1.5;
(2)当乙车间维修设备后,即2<x≤5时,设y与x的函数关系式为y=kx+b,
,
解得,
即当2<x≤5时,y与x的函数关系式为y=3.5x-5.5;
(3)由图2可得,
当x=2时,生产的疫苗有22-16.5=5.5(万支),
当2≤x≤5时,每天生产的疫苗有:16.5÷(5-2)=5.5(万支),
∴加工两天装满第一辆货车,再过1天装满第二辆货车.
26.解:(1)设,将A(4,0),B(0,4)代入得
,解得,
即;
(2)设,由题意可得:
AOP是以AO为腰的等腰三角形
当时,则点与点重合,即
当时,,解得
则或
故点P的坐标为或或
