沪教版六年级数学上册第四章 圆和扇形面积 单元复习题(含解析)
文档属性
| 名称 | 沪教版六年级数学上册第四章 圆和扇形面积 单元复习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 00:00:00 | ||
图片预览



文档简介
第四章《圆和扇形面积》单元复习题
一、单选题
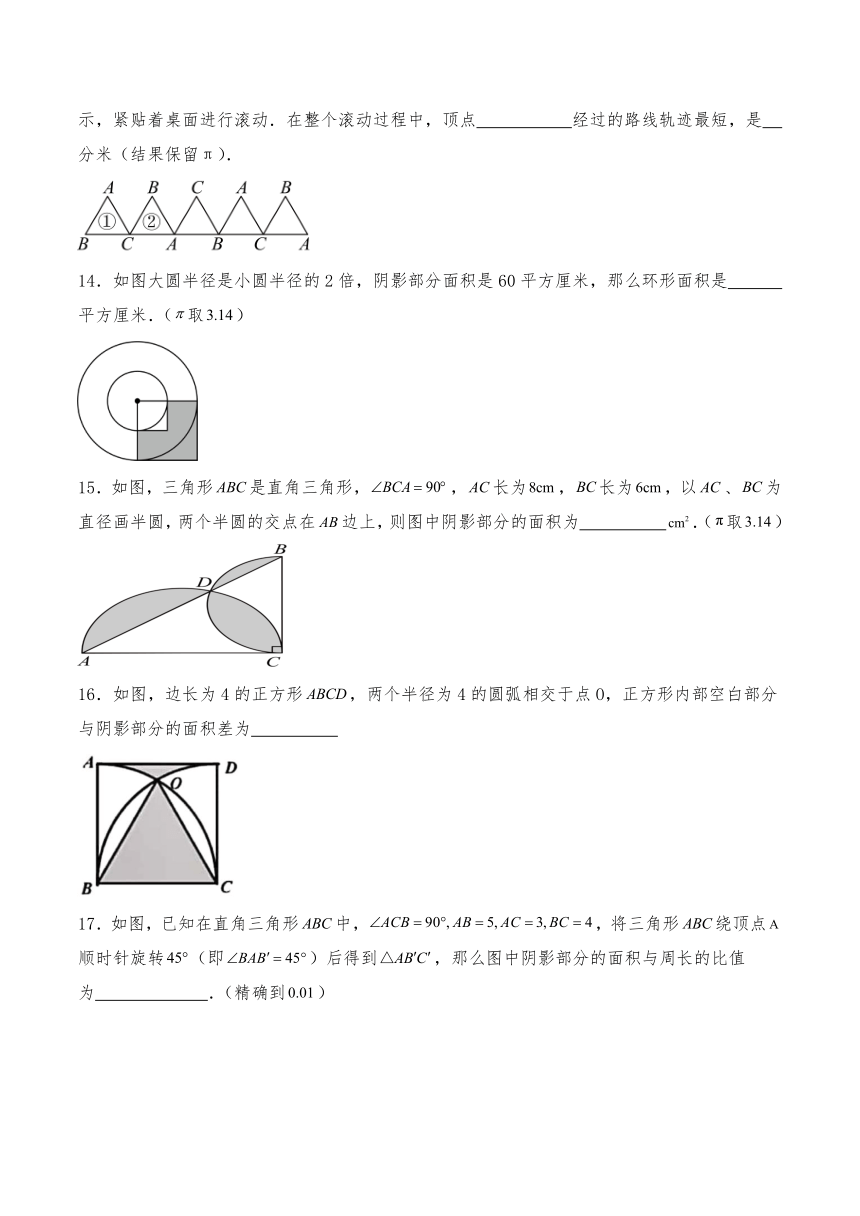
1.如图,正方形的边长是1厘米,4个弓形面积之和是( )平方厘米(取)
A. B. C. D.
2.如图所示,正方形中阴影部分的面积是( )
A. B. C. D.
3.如图,边长为的正方形池塘的周围是草地,池塘边P,Q,R,T处各有一棵树,且.现用一根长的绳子将一头羊栓在其中一棵树上,为了使羊在草地上活动区域的面积最大,应将绳子的另一端拴在( )
A.P处 B.Q处 C.R处 D.T处
4.如图1和2,两个圆的半径相等,O1、O2分别是两圆的圆心,图1中的阴影部分面积为S1,图2中的阴影部分面积为S2,那么S1与S2之间的大小关系是( )
A.S1<S2 B.S1=S2 C.S1>S2 D.不能确定
5.下列四个图案中,哪个图案的阴影部分面积与其他三个不相等( )
A. B.
C. D.
6.将一个圆平均分成1000个完全相同的的小扇形,拼成近似的长方形后,长方形的周长比圆的周长长8厘米,则圆的面积是( )平方厘米.
A.16π B.64π C.128π
7.一片草地上有一个木桩,把一只羊用6米长的绳子拴在木桩上,羊能吃到36π平方米的草,若把绳子延长1米,则羊能多吃到( )平方米的草.
A.π B.13π C.49π
8.如图,外面一个大圆,中间两个小圆,则大圆和两个小圆的周长比较结果是( ).
A.外圆大于两个小圆之和 B.外圆小于两个小圆之和
C.外圆等于两个小圆之和 D.无法确定
9.如图,阴影部分面积和的和是(结果保留)( )
A. B. C. D.
10.一个铁环直径是60厘米,从操场东端滚到西端转了90圈,另一个铁环的直径是40厘米,它从东端滚到西端要转的圈数是( ).
A.270 B.135 C.100 D.120
二、填空题
11.如图,边长为和的两个正方形并排放在一起,则阴影部分的面积是 .(结果保留)
12.如图,一张圆形纸片剪开成甲乙两个扇形,若甲扇形所在的弧长是,乙扇形所在的弧长为,那么甲扇形的圆心角比乙扇形的圆心角大 度.
13.桌面上平放着一个边长为2分米的等边三角形ABC(如图①),现将这个三角形按下图所示,紧贴着桌面进行滚动.在整个滚动过程中,顶点 经过的路线轨迹最短,是 分米(结果保留π).
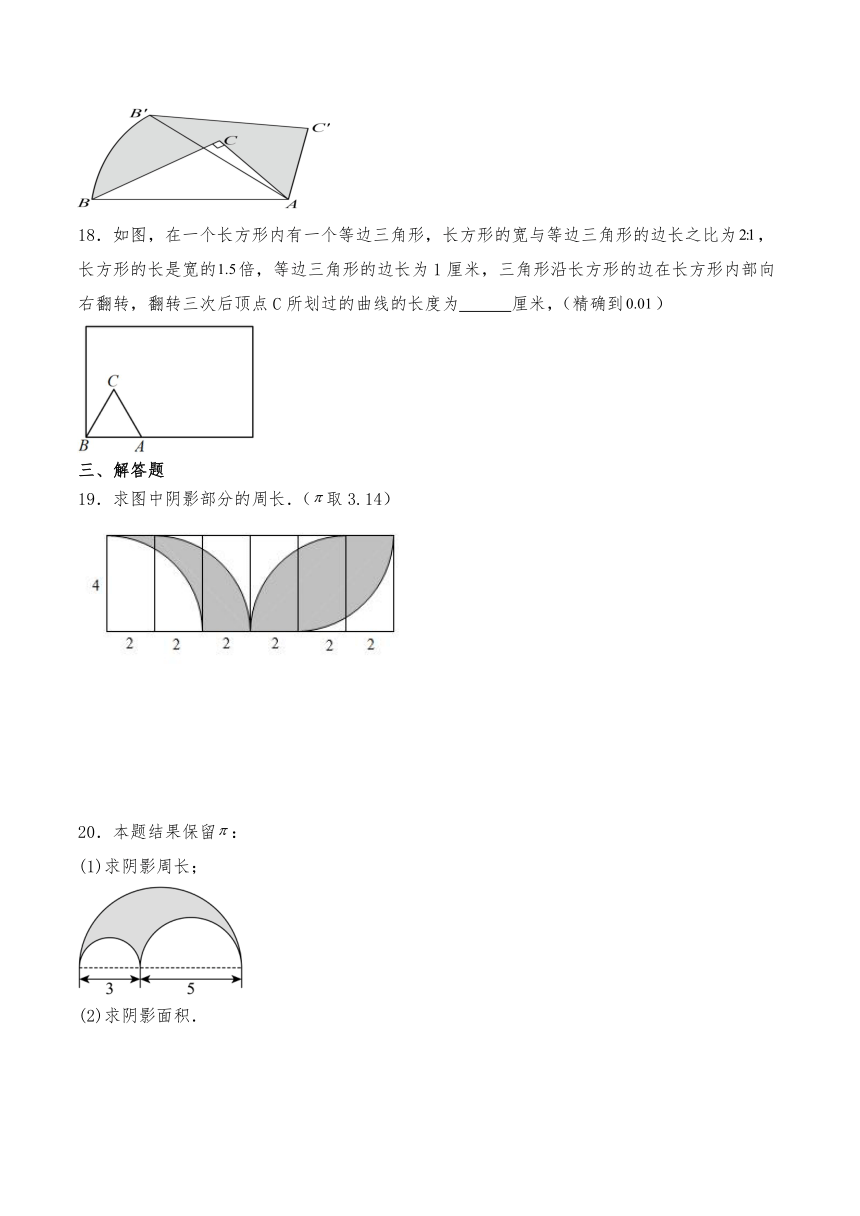
14.如图大圆半径是小圆半径的2倍,阴影部分面积是60平方厘米,那么环形面积是 平方厘米.(取)
15.如图,三角形是直角三角形,,长为,长为,以、为直径画半圆,两个半圆的交点在边上,则图中阴影部分的面积为 .(取)
16.如图,边长为4的正方形,两个半径为4的圆弧相交于点O,正方形内部空白部分与阴影部分的面积差为
17.如图,已知在直角三角形中,,将三角形绕顶点顺时针旋转(即)后得到,那么图中阴影部分的面积与周长的比值为 .(精确到)
18.如图,在一个长方形内有一个等边三角形,长方形的宽与等边三角形的边长之比为,长方形的长是宽的倍,等边三角形的边长为1厘米,三角形沿长方形的边在长方形内部向右翻转,翻转三次后顶点C所划过的曲线的长度为 厘米,(精确到)
三、解答题
19.求图中阴影部分的周长.(取3.14)
20.本题结果保留:
(1)求阴影周长;
(2)求阴影面积.
21.如图,点、点在线段上, 米, 米,是圆心.从到有3条不同的半圆弧线路可走,请你判断走哪一条半圆弧线路的距离最短.
22.(1)求阴影部分的周长.
(2)如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积.(,四舍五入,结果保留两位小数.)
23.如图,为进一步开展“睡眠管理”工作,某校对某年级部分学生的睡眠情况进行了问卷调查,并将调查结果绘制成了扇形统计图.其中A表示平均睡眠时间小于7小时的学生人数,表示平均睡眠时间在7小时到9小时之间的学生人数,表示平均睡眠时间在9小时以上的学生人数,A的学生人数与的学生人数恰好相等.请结合图中提供的信息解答下列问题:
(1)在扇形统计图中,表示A的扇形的圆心角是 度;
(2)A和的学生人数之和比的学生人数少 %(百分号前保留一位小数);
(3)如果的学生人数比A的学生人数多33人,那么本次调查的学生总人数是 人;
(4)你的平均睡眠时间是 (填A、、中的一个).
24.如图,两个圆周只有一个公共点,大圆直径为48厘米,小圆直径为30厘米,甲、乙两虫同时从点出发,甲虫以每秒0.5厘米的速度顺时针沿大圆圆周爬行,乙虫以同样速度顺时针沿小圆圆周爬行.(取3)
(1)问乙虫第一次爬回到点时,需要多少秒?此时甲虫是否已经经过点?
(2)两虫沿各自圆周不间断地反复爬行,能否出现这样的情况:乙虫爬回到点时甲虫恰好爬到点?如果可能,求此时乙虫至少爬了几圈;如果不可能,请说明理由.
25.圆形是自然界中最完美的形状之一,具有独特的美感和魅力,它通过一种简单的方式展现了和谐和平衡.小红同学在学习了圆之后,设计了一个以圆为主体的图案,如图所示,它是由三个圆组成,其中最小圆半径与最大圆半径的比是,中圆半径与最小圆半径的比是,已知最大圆的周长为.(取)
(1)求中圆的半径;
(2)图中分别用红色、黄色、蓝色填涂阴影部分,其中蓝色部分面积是红色部分面积与黄色部分面积之和的,红色部分面积是黄色部分面积的,分别求红色部分面积和黄色部分面积;
(3)为了使图案更加精美,小红在空白区域内镶嵌银色水钻,每平方厘米所需银色水钻的原价是元,购买时正赶上商家促销,每平方厘米现价比原价少,求小红购买银色水钻花了多少钱?
26.甲场地如图 a 所示,中间为一长 100m,宽为 60m 的长方形,两边为两个半圆,现欲在甲场地上铺一层厚 3cm 的煤.乙地为一售煤点,该售煤点有一堆煤近似于一个圆锥,如图 b所示,该圆锥底面圆的直径为 20m,高3m. (π取 3.14)
(1)甲场地需用的煤为多少立方米 乙地售煤点的这堆煤是否够用 说明理由;
(2)甲地有A型货车及B型货车,A型车每辆可载煤,每辆 A 型车的载煤体积是每辆B 型车载煤体积的,现甲地有 A 型货车 10 辆去乙地运煤,至少还需几辆 B型货车,才能将甲地所需的煤一次从乙地运回
27.正方形的边长为4厘米.
(1)分别以点A、C为圆心,4厘米为半径的弧、弧与边、所形成的阴影部分如图1,求图1阴影部分的面积.
(2)以点B为圆心,4厘米为半径的弧与以、为直径的两个半圆所形成的阴影部分如图2,求图2阴影部分的面积.
(3)若以为直径的半圆与三角形的边、所形成的阴影部分如图3,请试求图3阴影部分的面积.
答案
一、单选题
1.B
【分析】本题考查了正方形的性质和扇形面积计算,分别用四个扇形的面积减去四个等腰直角三角形的面积,再求和即可.能求出各个扇形的半径是解此题的关键.
【解析】解:∵,
∴,
∴,
∴,
∴
(平方厘米),
故4个弓形(阴影部分)面积之和是平方厘米.
故选:B.
2.B
【分析】阴影面积为正方形面积大圆的面积小圆的面积,据此列式计算可得.
【解析】解:阴影部分的面积为
.
故选:B.
3.C
【分析】根据圆的面积计算公式,以及扇形的面积公式,即可求得栓在各点时的活动区域的面积,即可作出判断.
【解析】解:将羊拴在Q处时,活动区域的面积是:;
将羊拴在R处时,活动区域的面积是:;
将羊拴在T处时,活动区域的面积是:;
将羊拴在P处时,活动区域的面积是:;
故拴在R处时,可使羊的活动范围最大.
故选:C.
4.A
【分析】设两个圆的半径都是r,则图1中正方形的边长是2r,由图2中正方形的面积是4个直角三角形面积的和可得正方形的边长为r;再根据正方形和圆的面积公式计算S1、S2的值,计算S1﹣S2的值即可判断;
【解析】解:设两个圆的半径都是r,则图1中正方形的边长是2r,
∵图2中正方形的面积是4个直角三角形面积的和:4×r×r=2r2,
∴图2中正方形的边长是r,
则S1=2r×2r﹣πr2=4r2﹣πr2,S2=πr2﹣r×r=πr2﹣2r2,
S1﹣S2=(4r2﹣πr2)﹣(πr2﹣2r2)=6r2﹣2πr2=(6﹣2π)r2,
∵6﹣2π<0,
∴S1﹣S2<0,
∴S1<S2,
故选: A.
5.B
【分析】运用圆的面积,正方形的面积,扇形的面积,先计算出每个阴影部分的面积,比较大小即可.
【解析】设正方形的边长为2a,
∴A选项中阴影部分的面积为:;
设扇形的半径为x,
∴B选项中阴影部分的面积为:;
∴C选项中阴影部分的面积为:;
∴D选项中阴影部分的面积为:;
故选B.
6.A
【分析】把一个圆等分成若干个小扇形后拼成一个近似的长方形,周长比原来增加了8厘米,是因为近似的长方形的周长比圆的周长多了圆的两个半径.据此可求出圆的半径,然后求圆的面积即可.
【解析】解:圆的半径为:8÷2=4(厘米),
圆的面积为:π×4×4=16π.
故选A.
7.B
【分析】由题意可得养原来吃草的区域为半径为6的圆,绳子延长1米,则半径变成7米,然后求出圆的面积,最后减去36π即可解答.
【解析】解:由题意可得:绳子延长1米,羊吃草区域的半径为7米
则:该区域的面积为:72π=49π
羊能多吃到草的面积为:49π-36π=13π.
故选B.
8.C
【分析】根据圆周长的计算公式分析,即可完成求解.
【解析】结合题意得:小圆的直径是大圆的一半
假设小圆的直径是m,则大圆的直径为2m
∴小圆的周长,大圆的周长
∴两个小圆的周长之和
∴大圆的周长=两个小圆的周长之和
即外圆等于两个小圆之和
故选:C.
9.C
【分析】根据图形,阴影部分面积的和,即长为12,宽为4的长方形面积减去空白部分面积,最左侧空白部分是半径为4的四分之一圆的面积,其余空白部分可以看做是三个同样的部分,每部分都是边长为4的正方形面积减去一个半径为4的四分之一圆的面积,从而求解.
【解析】解:由题意可得:阴影部分面积和的和是
=
=
=.
故选:C.
10.B
【分析】已知一个铁环直径是60厘米,可计算的其周长,再结合滚动的圈数即可计算得操场东端滚到西端长度,再根据另一个铁环的直径,即可求出其周长和它从东端滚到西端要转的圈数.
【解析】∵一个铁环直径是60厘米
∴铁环周长=直径=
∵铁环从操场东端滚到西端转了90圈
∴操场东端滚到西端长度
∵另一个铁环的直径是40厘米
∴另一个铁环周长直径
∵另一个铁环从东端滚到西端要转的圈数操场东端滚到西长度铁环周长
∴另一个铁环从东端滚到西端要转的圈数
故选:B.
二、填空题
11.
【分析】根据进行计算即可.
【解析】解:如图,
∵四边形,是正方形,
∴,
∴
,
故答案为:.
12.72
【分析】由题意可知:甲扇形的弧长占圆的周长的,则其圆心角也占圆的度数的;乙扇形的弧长占圆的周长的,则其圆心角也占圆的度数的;即可得出正确答案.
【解析】解:甲扇形的圆心角度数为:
,
,
,
乙扇形的圆心角度数为:
,
,
,
,
所以,甲扇形的圆心角比乙扇形的圆心角大度.
故答案为:
13. C
【分析】在滚动的过程中,每个顶点每次经过的路线轨迹就是一个半径是2分米,圆心角是的扇形的圆弧,顶点A和顶点B经过的路线轨迹都是3个圆弧,顶点C经过的路线轨迹是2个圆弧,所以顶点C经过的路线轨迹最短,根据圆弧长度的计算方法,计算即可.
【解析】解:根据题意,在滚动的过程中,每个顶点每次经过的路线轨迹就是一个半径是2分米,圆心角是的扇形的圆弧,顶点A和顶点B经过的路线轨迹都是3个圆弧,顶点C经过的路线轨迹是2个圆弧,所以顶点C经过的路线轨迹最短,
最短长度为,
故答案为:C;.
14.188.4
【分析】设小圆的半径是r,则大圆的半径是2r,由阴影部分的面积为60平方厘米,可得,根据环形的面积为,计算求解即可.
【解析】解:设小圆的半径是r,则大圆的半径是2r.
∵阴影部分的面积为60平方厘米,
∴,
∴环形的面积为(平方厘米),
故答案为:188.4.
15.
【分析】利用两个半圆的面积之和减去三角形的面积进行求解即可.
【解析】解:设各个部分的面积为:,如图所示,
因为两个半圆的面积和是:,的面积是,阴影部分的面积是:,
所以图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积.
故答案为:.
16.
【分析】先根据图形性质判断,再分别求解空白部分的面积与阴影部分的面积,从而可得答案.
【解析】解:由题意可得:
,,,,
∴,
所以空白部分的两个扇形面积相等,
所以空白部分的面积为:,
所以阴影部分的面积为:,
∴正方形内部阴影部分与空白部分的面积差为
,
故答案为:.
17.
【分析】阴影部分的面积等于扇形的面积,阴影部分的周长等于的长,再加上弧的长,由此即可得.
【解析】解:由旋转的性质得:,的面积等于的面积,
,
阴影部分的面积为,
阴影部分的周长为,
则图中阴影部分的面积与周长的比值为,
故答案为:.
18.
【分析】首先画出图形,求出长方形的长与宽,再根据弧长公式,即可求得.
【解析】解:翻转三次后顶点C所划过的曲线如图:
等边三角形的边长为1厘米,长方形的宽与等边三角形的边长之比为,
长方形的宽为2厘米,,
长方形的长是宽的倍,
长方形的长是(厘米),
第一次翻转后点C落在处,第二次翻转后点没动,第三次翻转后点落在处,
第一次翻转后点C所划过的曲线的长度为弧的长,第三次翻转后点所划过的曲线的长度为弧的长,
,,
翻转三次后顶点C所划过的曲线的长度为:
(厘米),
故答案为:.
三、解答题
19.故阴影部分的周长为:
3.14×4×2+2×4=33.12
20.(1)解:大半圆的圆弧长,
中等半圆的圆弧长,
小半圆的圆弧长,
所以阴影周长;
(2)解:由图可知阴影面积即为长方形面积,
所以阴影面积为.
21.解:根据题意可得:
路线距离为:米,
路线距离为:米,
路线距离为:米,
故三条路距离一样长.
22.解:(1)如图:
(2)
23.(1)解:∵B所占百分比为,A的学生人数与C的学生人数恰好相等,
∴A与C所占百分比均为,
∴A的扇形的圆心角是.
故答案为:54;
(2).
故答案为:40;
(3)(人).
故答案为:60;
(4)我的平均睡眠时间为6.5小时,选择A.
故答案为:A.
24.(1)
(秒)
甲虫走的路程>72,此时甲虫已经经过点;
答:乙虫第一次爬回到点时,需要180秒。此时甲虫已经经过点.
(2) 90与72的最小公倍数是360,360÷90=4(圈)
此时乙虫至少爬了4圈
25.(1)解:∵最大圆的周长为.
∴大圆的半径为
∵最小圆半径与最大圆半径的比是,中圆半径与最小圆半径的比是,
∴最小圆的半径为,中圆半径为;
(2)解:蓝色部分面积是小圆的面积,即,
∵蓝色部分面积是红色部分面积与黄色部分面积之和的,
∴红色部分面积与黄色部分面积之和为,
∵红色部分面积是黄色部分面积的,
∴黄色部分面积,
红色部分面积为,
答:红色部分面积为,黄色部分面积为;
(3)解:空白区域内的面积为,
,
∴小红购买银色水钻花了元,
答:小红购买银色水钻花了.
26.(1)解:甲场地的面积.
则甲场地需要煤的总体积.
乙地有煤的体积.
∵,
∴乙地的煤不够用;
(2)解:一辆B型车的载重体积.
设需要B型车x辆,根据题意得;.
解得:.
∴至少需要B型车10.
答:至少需要B型车10.
27.(1)解:∵四边形为正方形,
∴,
∴
(平方厘米);
(2)解∶如图2,连接,,交点为O,
则可将阴影①绕点O顺时针旋转至③,将阴影②绕点O逆时针旋转至④,
则
(平方厘米);
(3)如图3,将阴影①沿的垂直平分线翻折至②,
则,
∵厘米,
∴(平方厘米),
∴(平方厘米).
一、单选题
1.如图,正方形的边长是1厘米,4个弓形面积之和是( )平方厘米(取)
A. B. C. D.
2.如图所示,正方形中阴影部分的面积是( )
A. B. C. D.
3.如图,边长为的正方形池塘的周围是草地,池塘边P,Q,R,T处各有一棵树,且.现用一根长的绳子将一头羊栓在其中一棵树上,为了使羊在草地上活动区域的面积最大,应将绳子的另一端拴在( )
A.P处 B.Q处 C.R处 D.T处
4.如图1和2,两个圆的半径相等,O1、O2分别是两圆的圆心,图1中的阴影部分面积为S1,图2中的阴影部分面积为S2,那么S1与S2之间的大小关系是( )
A.S1<S2 B.S1=S2 C.S1>S2 D.不能确定
5.下列四个图案中,哪个图案的阴影部分面积与其他三个不相等( )
A. B.
C. D.
6.将一个圆平均分成1000个完全相同的的小扇形,拼成近似的长方形后,长方形的周长比圆的周长长8厘米,则圆的面积是( )平方厘米.
A.16π B.64π C.128π
7.一片草地上有一个木桩,把一只羊用6米长的绳子拴在木桩上,羊能吃到36π平方米的草,若把绳子延长1米,则羊能多吃到( )平方米的草.
A.π B.13π C.49π
8.如图,外面一个大圆,中间两个小圆,则大圆和两个小圆的周长比较结果是( ).
A.外圆大于两个小圆之和 B.外圆小于两个小圆之和
C.外圆等于两个小圆之和 D.无法确定
9.如图,阴影部分面积和的和是(结果保留)( )
A. B. C. D.
10.一个铁环直径是60厘米,从操场东端滚到西端转了90圈,另一个铁环的直径是40厘米,它从东端滚到西端要转的圈数是( ).
A.270 B.135 C.100 D.120
二、填空题
11.如图,边长为和的两个正方形并排放在一起,则阴影部分的面积是 .(结果保留)
12.如图,一张圆形纸片剪开成甲乙两个扇形,若甲扇形所在的弧长是,乙扇形所在的弧长为,那么甲扇形的圆心角比乙扇形的圆心角大 度.
13.桌面上平放着一个边长为2分米的等边三角形ABC(如图①),现将这个三角形按下图所示,紧贴着桌面进行滚动.在整个滚动过程中,顶点 经过的路线轨迹最短,是 分米(结果保留π).
14.如图大圆半径是小圆半径的2倍,阴影部分面积是60平方厘米,那么环形面积是 平方厘米.(取)
15.如图,三角形是直角三角形,,长为,长为,以、为直径画半圆,两个半圆的交点在边上,则图中阴影部分的面积为 .(取)
16.如图,边长为4的正方形,两个半径为4的圆弧相交于点O,正方形内部空白部分与阴影部分的面积差为
17.如图,已知在直角三角形中,,将三角形绕顶点顺时针旋转(即)后得到,那么图中阴影部分的面积与周长的比值为 .(精确到)
18.如图,在一个长方形内有一个等边三角形,长方形的宽与等边三角形的边长之比为,长方形的长是宽的倍,等边三角形的边长为1厘米,三角形沿长方形的边在长方形内部向右翻转,翻转三次后顶点C所划过的曲线的长度为 厘米,(精确到)
三、解答题
19.求图中阴影部分的周长.(取3.14)
20.本题结果保留:
(1)求阴影周长;
(2)求阴影面积.
21.如图,点、点在线段上, 米, 米,是圆心.从到有3条不同的半圆弧线路可走,请你判断走哪一条半圆弧线路的距离最短.
22.(1)求阴影部分的周长.
(2)如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积.(,四舍五入,结果保留两位小数.)
23.如图,为进一步开展“睡眠管理”工作,某校对某年级部分学生的睡眠情况进行了问卷调查,并将调查结果绘制成了扇形统计图.其中A表示平均睡眠时间小于7小时的学生人数,表示平均睡眠时间在7小时到9小时之间的学生人数,表示平均睡眠时间在9小时以上的学生人数,A的学生人数与的学生人数恰好相等.请结合图中提供的信息解答下列问题:
(1)在扇形统计图中,表示A的扇形的圆心角是 度;
(2)A和的学生人数之和比的学生人数少 %(百分号前保留一位小数);
(3)如果的学生人数比A的学生人数多33人,那么本次调查的学生总人数是 人;
(4)你的平均睡眠时间是 (填A、、中的一个).
24.如图,两个圆周只有一个公共点,大圆直径为48厘米,小圆直径为30厘米,甲、乙两虫同时从点出发,甲虫以每秒0.5厘米的速度顺时针沿大圆圆周爬行,乙虫以同样速度顺时针沿小圆圆周爬行.(取3)
(1)问乙虫第一次爬回到点时,需要多少秒?此时甲虫是否已经经过点?
(2)两虫沿各自圆周不间断地反复爬行,能否出现这样的情况:乙虫爬回到点时甲虫恰好爬到点?如果可能,求此时乙虫至少爬了几圈;如果不可能,请说明理由.
25.圆形是自然界中最完美的形状之一,具有独特的美感和魅力,它通过一种简单的方式展现了和谐和平衡.小红同学在学习了圆之后,设计了一个以圆为主体的图案,如图所示,它是由三个圆组成,其中最小圆半径与最大圆半径的比是,中圆半径与最小圆半径的比是,已知最大圆的周长为.(取)
(1)求中圆的半径;
(2)图中分别用红色、黄色、蓝色填涂阴影部分,其中蓝色部分面积是红色部分面积与黄色部分面积之和的,红色部分面积是黄色部分面积的,分别求红色部分面积和黄色部分面积;
(3)为了使图案更加精美,小红在空白区域内镶嵌银色水钻,每平方厘米所需银色水钻的原价是元,购买时正赶上商家促销,每平方厘米现价比原价少,求小红购买银色水钻花了多少钱?
26.甲场地如图 a 所示,中间为一长 100m,宽为 60m 的长方形,两边为两个半圆,现欲在甲场地上铺一层厚 3cm 的煤.乙地为一售煤点,该售煤点有一堆煤近似于一个圆锥,如图 b所示,该圆锥底面圆的直径为 20m,高3m. (π取 3.14)
(1)甲场地需用的煤为多少立方米 乙地售煤点的这堆煤是否够用 说明理由;
(2)甲地有A型货车及B型货车,A型车每辆可载煤,每辆 A 型车的载煤体积是每辆B 型车载煤体积的,现甲地有 A 型货车 10 辆去乙地运煤,至少还需几辆 B型货车,才能将甲地所需的煤一次从乙地运回
27.正方形的边长为4厘米.
(1)分别以点A、C为圆心,4厘米为半径的弧、弧与边、所形成的阴影部分如图1,求图1阴影部分的面积.
(2)以点B为圆心,4厘米为半径的弧与以、为直径的两个半圆所形成的阴影部分如图2,求图2阴影部分的面积.
(3)若以为直径的半圆与三角形的边、所形成的阴影部分如图3,请试求图3阴影部分的面积.
答案
一、单选题
1.B
【分析】本题考查了正方形的性质和扇形面积计算,分别用四个扇形的面积减去四个等腰直角三角形的面积,再求和即可.能求出各个扇形的半径是解此题的关键.
【解析】解:∵,
∴,
∴,
∴,
∴
(平方厘米),
故4个弓形(阴影部分)面积之和是平方厘米.
故选:B.
2.B
【分析】阴影面积为正方形面积大圆的面积小圆的面积,据此列式计算可得.
【解析】解:阴影部分的面积为
.
故选:B.
3.C
【分析】根据圆的面积计算公式,以及扇形的面积公式,即可求得栓在各点时的活动区域的面积,即可作出判断.
【解析】解:将羊拴在Q处时,活动区域的面积是:;
将羊拴在R处时,活动区域的面积是:;
将羊拴在T处时,活动区域的面积是:;
将羊拴在P处时,活动区域的面积是:;
故拴在R处时,可使羊的活动范围最大.
故选:C.
4.A
【分析】设两个圆的半径都是r,则图1中正方形的边长是2r,由图2中正方形的面积是4个直角三角形面积的和可得正方形的边长为r;再根据正方形和圆的面积公式计算S1、S2的值,计算S1﹣S2的值即可判断;
【解析】解:设两个圆的半径都是r,则图1中正方形的边长是2r,
∵图2中正方形的面积是4个直角三角形面积的和:4×r×r=2r2,
∴图2中正方形的边长是r,
则S1=2r×2r﹣πr2=4r2﹣πr2,S2=πr2﹣r×r=πr2﹣2r2,
S1﹣S2=(4r2﹣πr2)﹣(πr2﹣2r2)=6r2﹣2πr2=(6﹣2π)r2,
∵6﹣2π<0,
∴S1﹣S2<0,
∴S1<S2,
故选: A.
5.B
【分析】运用圆的面积,正方形的面积,扇形的面积,先计算出每个阴影部分的面积,比较大小即可.
【解析】设正方形的边长为2a,
∴A选项中阴影部分的面积为:;
设扇形的半径为x,
∴B选项中阴影部分的面积为:;
∴C选项中阴影部分的面积为:;
∴D选项中阴影部分的面积为:;
故选B.
6.A
【分析】把一个圆等分成若干个小扇形后拼成一个近似的长方形,周长比原来增加了8厘米,是因为近似的长方形的周长比圆的周长多了圆的两个半径.据此可求出圆的半径,然后求圆的面积即可.
【解析】解:圆的半径为:8÷2=4(厘米),
圆的面积为:π×4×4=16π.
故选A.
7.B
【分析】由题意可得养原来吃草的区域为半径为6的圆,绳子延长1米,则半径变成7米,然后求出圆的面积,最后减去36π即可解答.
【解析】解:由题意可得:绳子延长1米,羊吃草区域的半径为7米
则:该区域的面积为:72π=49π
羊能多吃到草的面积为:49π-36π=13π.
故选B.
8.C
【分析】根据圆周长的计算公式分析,即可完成求解.
【解析】结合题意得:小圆的直径是大圆的一半
假设小圆的直径是m,则大圆的直径为2m
∴小圆的周长,大圆的周长
∴两个小圆的周长之和
∴大圆的周长=两个小圆的周长之和
即外圆等于两个小圆之和
故选:C.
9.C
【分析】根据图形,阴影部分面积的和,即长为12,宽为4的长方形面积减去空白部分面积,最左侧空白部分是半径为4的四分之一圆的面积,其余空白部分可以看做是三个同样的部分,每部分都是边长为4的正方形面积减去一个半径为4的四分之一圆的面积,从而求解.
【解析】解:由题意可得:阴影部分面积和的和是
=
=
=.
故选:C.
10.B
【分析】已知一个铁环直径是60厘米,可计算的其周长,再结合滚动的圈数即可计算得操场东端滚到西端长度,再根据另一个铁环的直径,即可求出其周长和它从东端滚到西端要转的圈数.
【解析】∵一个铁环直径是60厘米
∴铁环周长=直径=
∵铁环从操场东端滚到西端转了90圈
∴操场东端滚到西端长度
∵另一个铁环的直径是40厘米
∴另一个铁环周长直径
∵另一个铁环从东端滚到西端要转的圈数操场东端滚到西长度铁环周长
∴另一个铁环从东端滚到西端要转的圈数
故选:B.
二、填空题
11.
【分析】根据进行计算即可.
【解析】解:如图,
∵四边形,是正方形,
∴,
∴
,
故答案为:.
12.72
【分析】由题意可知:甲扇形的弧长占圆的周长的,则其圆心角也占圆的度数的;乙扇形的弧长占圆的周长的,则其圆心角也占圆的度数的;即可得出正确答案.
【解析】解:甲扇形的圆心角度数为:
,
,
,
乙扇形的圆心角度数为:
,
,
,
,
所以,甲扇形的圆心角比乙扇形的圆心角大度.
故答案为:
13. C
【分析】在滚动的过程中,每个顶点每次经过的路线轨迹就是一个半径是2分米,圆心角是的扇形的圆弧,顶点A和顶点B经过的路线轨迹都是3个圆弧,顶点C经过的路线轨迹是2个圆弧,所以顶点C经过的路线轨迹最短,根据圆弧长度的计算方法,计算即可.
【解析】解:根据题意,在滚动的过程中,每个顶点每次经过的路线轨迹就是一个半径是2分米,圆心角是的扇形的圆弧,顶点A和顶点B经过的路线轨迹都是3个圆弧,顶点C经过的路线轨迹是2个圆弧,所以顶点C经过的路线轨迹最短,
最短长度为,
故答案为:C;.
14.188.4
【分析】设小圆的半径是r,则大圆的半径是2r,由阴影部分的面积为60平方厘米,可得,根据环形的面积为,计算求解即可.
【解析】解:设小圆的半径是r,则大圆的半径是2r.
∵阴影部分的面积为60平方厘米,
∴,
∴环形的面积为(平方厘米),
故答案为:188.4.
15.
【分析】利用两个半圆的面积之和减去三角形的面积进行求解即可.
【解析】解:设各个部分的面积为:,如图所示,
因为两个半圆的面积和是:,的面积是,阴影部分的面积是:,
所以图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积.
故答案为:.
16.
【分析】先根据图形性质判断,再分别求解空白部分的面积与阴影部分的面积,从而可得答案.
【解析】解:由题意可得:
,,,,
∴,
所以空白部分的两个扇形面积相等,
所以空白部分的面积为:,
所以阴影部分的面积为:,
∴正方形内部阴影部分与空白部分的面积差为
,
故答案为:.
17.
【分析】阴影部分的面积等于扇形的面积,阴影部分的周长等于的长,再加上弧的长,由此即可得.
【解析】解:由旋转的性质得:,的面积等于的面积,
,
阴影部分的面积为,
阴影部分的周长为,
则图中阴影部分的面积与周长的比值为,
故答案为:.
18.
【分析】首先画出图形,求出长方形的长与宽,再根据弧长公式,即可求得.
【解析】解:翻转三次后顶点C所划过的曲线如图:
等边三角形的边长为1厘米,长方形的宽与等边三角形的边长之比为,
长方形的宽为2厘米,,
长方形的长是宽的倍,
长方形的长是(厘米),
第一次翻转后点C落在处,第二次翻转后点没动,第三次翻转后点落在处,
第一次翻转后点C所划过的曲线的长度为弧的长,第三次翻转后点所划过的曲线的长度为弧的长,
,,
翻转三次后顶点C所划过的曲线的长度为:
(厘米),
故答案为:.
三、解答题
19.故阴影部分的周长为:
3.14×4×2+2×4=33.12
20.(1)解:大半圆的圆弧长,
中等半圆的圆弧长,
小半圆的圆弧长,
所以阴影周长;
(2)解:由图可知阴影面积即为长方形面积,
所以阴影面积为.
21.解:根据题意可得:
路线距离为:米,
路线距离为:米,
路线距离为:米,
故三条路距离一样长.
22.解:(1)如图:
(2)
23.(1)解:∵B所占百分比为,A的学生人数与C的学生人数恰好相等,
∴A与C所占百分比均为,
∴A的扇形的圆心角是.
故答案为:54;
(2).
故答案为:40;
(3)(人).
故答案为:60;
(4)我的平均睡眠时间为6.5小时,选择A.
故答案为:A.
24.(1)
(秒)
甲虫走的路程>72,此时甲虫已经经过点;
答:乙虫第一次爬回到点时,需要180秒。此时甲虫已经经过点.
(2) 90与72的最小公倍数是360,360÷90=4(圈)
此时乙虫至少爬了4圈
25.(1)解:∵最大圆的周长为.
∴大圆的半径为
∵最小圆半径与最大圆半径的比是,中圆半径与最小圆半径的比是,
∴最小圆的半径为,中圆半径为;
(2)解:蓝色部分面积是小圆的面积,即,
∵蓝色部分面积是红色部分面积与黄色部分面积之和的,
∴红色部分面积与黄色部分面积之和为,
∵红色部分面积是黄色部分面积的,
∴黄色部分面积,
红色部分面积为,
答:红色部分面积为,黄色部分面积为;
(3)解:空白区域内的面积为,
,
∴小红购买银色水钻花了元,
答:小红购买银色水钻花了.
26.(1)解:甲场地的面积.
则甲场地需要煤的总体积.
乙地有煤的体积.
∵,
∴乙地的煤不够用;
(2)解:一辆B型车的载重体积.
设需要B型车x辆,根据题意得;.
解得:.
∴至少需要B型车10.
答:至少需要B型车10.
27.(1)解:∵四边形为正方形,
∴,
∴
(平方厘米);
(2)解∶如图2,连接,,交点为O,
则可将阴影①绕点O顺时针旋转至③,将阴影②绕点O逆时针旋转至④,
则
(平方厘米);
(3)如图3,将阴影①沿的垂直平分线翻折至②,
则,
∵厘米,
∴(平方厘米),
∴(平方厘米).
