2023-2024学年数学湘教版八年级下册期末题型专练—选择题B卷(含解析)
文档属性
| 名称 | 2023-2024学年数学湘教版八年级下册期末题型专练—选择题B卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 00:00:00 | ||
图片预览



文档简介
2023-2024学年数学湘教版八年级下册期末题型专练—选择题B卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小丽从常州开车去南京,开了一段时间后,发现油所剩不多了,于是开到服务区加油,加满油后又开始匀速行驶,下面哪一幅图可以近似的刻画该汽车在这段时间内的速度变化情况( )
A. B. C. D.
2.如图,有两条相互垂直的卡槽,一小哥将一根木棒的两端分别卡在卡槽中,在木棒的中部插有一支记号笔,接着移动木棒的一端,另一端也随之移动.我们惊讶地发现:记号笔画出了一段圆弧!根据你所学的有关直角三角形的知识,分析“木棒作弧”中所运用的数学道理是( )
A.直角三角形的两直角边长度的平方和等于第三边长度的平方
B.直角三角形的面积等于两直角边乘积的一半
C.直角三角形的两个锐角互余
D.直角三角形斜边上的中线等于斜边的一半
3.已知点在第二象限,且m为整数,则m的值是( )
A.0 B.1 C.2 D.3
4.在平面直角坐标系中,,,若点在直线上,且,则点M的坐标为( )
A. B.或 C. D.或
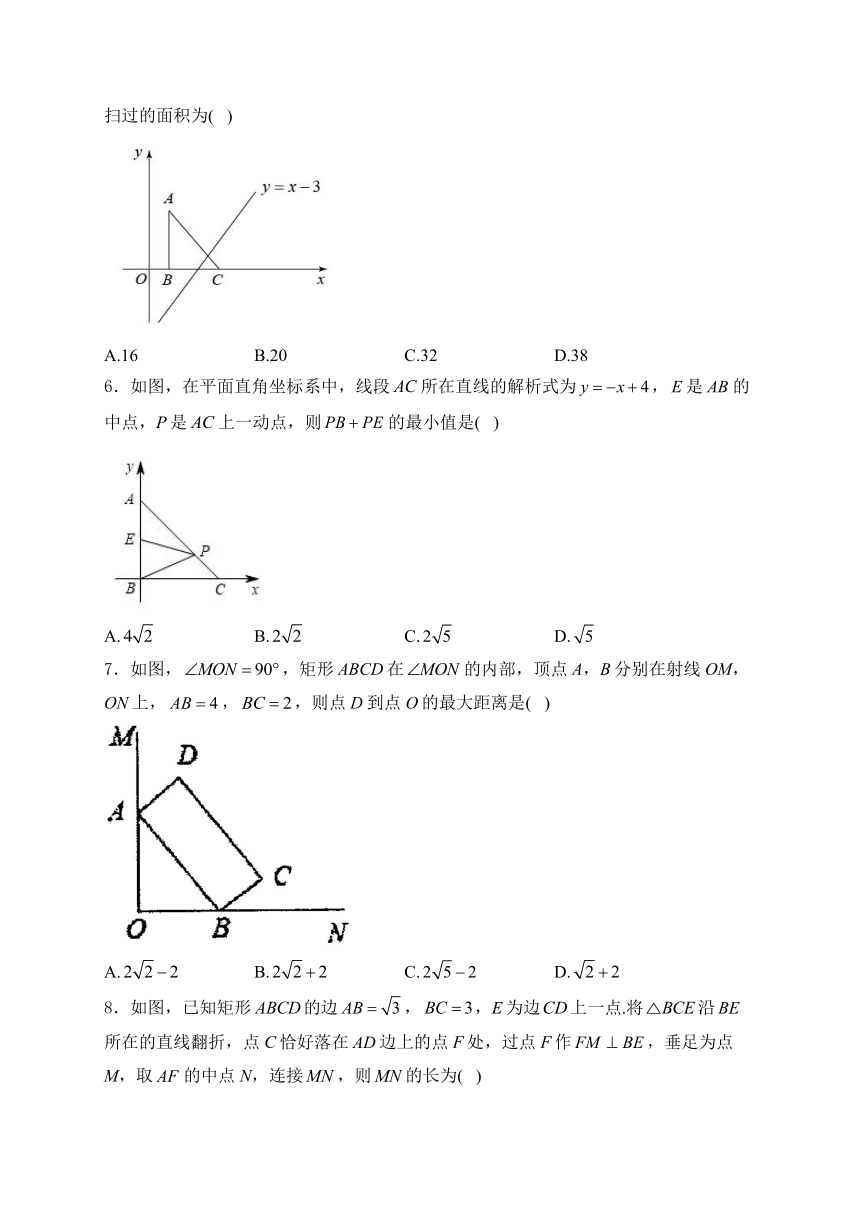
5.如图,在平面直角坐标系内,其中,.点B,C的坐标分别为,.将沿x轴向右平移,当点A在直线时,线段扫过的面积为( )
A.16 B.20 C.32 D.38
6.如图,在平面直角坐标系中,线段所在直线的解析式为,是的中点,P是上一动点,则的最小值是( )
A. B. C. D.
7.如图,,矩形ABCD在的内部,顶点A,B分别在射线OM,ON上,,,则点D到点O的最大距离是( )
A. B. C. D.
8.如图,已知矩形的边,,E为边上一点.将沿所在的直线翻折,点C恰好落在边上的点F处,过点F作,垂足为点M,取的中点N,连接,则的长为( )
A.3 B. C. D.
9.为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:
①这次调查属于全面调查
②这次调查共抽取了名学生
③这次调查阅读所用时间在的人数最少
④这次调查阅读所用时间在的人数占所调查人数的,其中正确的有( ).
A.②③④ B.①③④ C.①②④ D.①②③
10.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,,F是AB边上一点,将沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A. B. C.1 D.
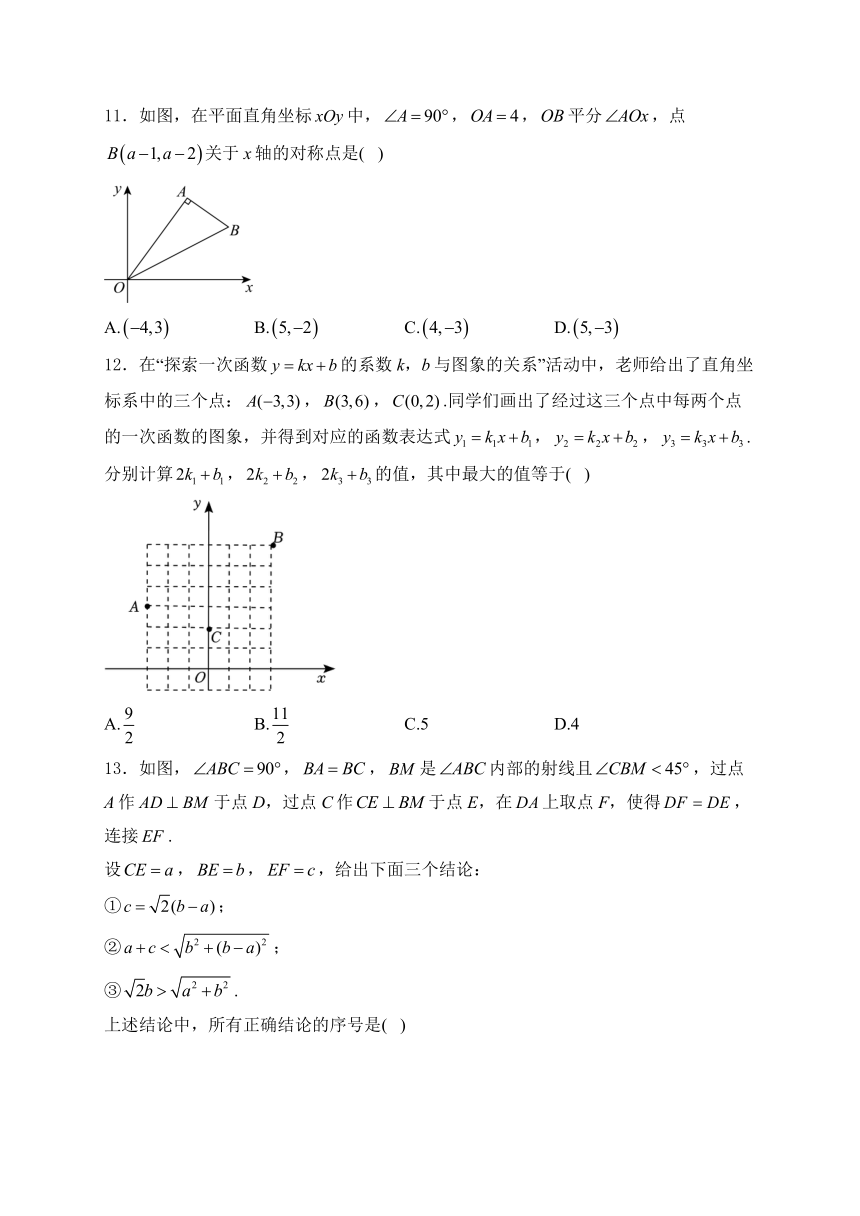
11.如图,在平面直角坐标中,,,平分,点关于x轴的对称点是( )
A. B. C. D.
12.在“探索一次函数的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:,,.同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式,,.分别计算,,的值,其中最大的值等于( )
A. B. C.5 D.4
13.如图,,,是内部的射线且,过点A作于点D,过点C作于点E,在上取点F,使得,连接.
设,,,给出下面三个结论:
①;
②;
③.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
参考答案
1.答案:B
解析:汽车经历:加速-匀速-减速到站-加速-匀速,
加速:速度增加,
匀速:速度保持不变,
减速:速度下降,
到站:速度为0.
观察四个选项的图象是否符合题干要求,只有B选项符合.
故选B.
2.答案:D
解析:因为“木棒作弧”过程中弧上的点到两条相互垂直的卡槽交点距离相等,且木棒作为三角形的斜边,记号笔在木棒的中点,
所以运用了直角三角形斜边上的中线等于斜边的一半,
故选:D.
3.答案:B
解析:点在第二象限,
,
解得:,
m为整数,
,
故选:B.
4.答案:B
解析:,,
与y轴平行,A、B两点的横坐标相同,又,
,点M在直线上,
,
M点纵坐标为:或,
M点的坐标为:或,
故选:B.
5.答案:B
解析:点B,C的坐标分别为,
,.
当点A落在直线时,
解得
平移后点B(7,0)
平移了个单位
线段扫过的面积为
故选B.
6.答案:C
解析:作点B关于的对称点,连接交于,
此时,的值最小,最小值为的长,
线段所在直线的解析式为,
,,
,,
是的中点,
,
是点B关于的对称点,
,,,
四边形是正方形,
,
的最小值是.
故选:C.
7.答案:B
解析:取AB中点E,连接OE、DE、OD,
,
.
在中,利用勾股定理可得.
在中,根据三角形三边关系可知,
当O、E、D点共线时,OD最大为.
故选:B.
8.答案:D
解析:如图所示连接,.
由翻折的性质可知,垂直平分线段,
,
又,
F,M,C共线,
,
四边形是矩形,
,
,
N是的中点,M是的中点,
是的中位线,
.
故选:D.
9.答案:A
解析:这次调查属于抽样调查,故①错误;
结合频数分布直方图,可计算得共抽取名学生,故②正确;
结合频数分布直方图,阅读所用时间在的共8名学生,人数最少,故③正确;
这次调查阅读所用时间在的人数占比为,即,故④正确;
故选:A.
10.答案:B
解析:四边形是边长为4的正方形,
,,
,
由翻折得,,垂直平分,
在和中,
,
,
,
,
,
,
,且,
,
解得,
,
,
解得,
故选:B.
11.答案:C
解析:如图,过B点作轴于点C,则,
,
平分,
,
又,
,
,即,,
,
关于x轴的对称点的坐标为,
故选:C.
12.答案:B
解析:不妨设直线的函数表达式为,直线的函数表达式为,直线的函数表达式为,
将,代入得:,
解得:,
.
同理,可求出,,
,.
又,
其中最大的值等于.
故选:B.
13.答案:B
解析:,,
,
,
,,
,
在和中,
,
,
,,
,
,
,故①正确,
连接,则,
,,
,
,
,故②错误,
是内部的射线且,
,
,
,
,故③正确.
故选:B.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小丽从常州开车去南京,开了一段时间后,发现油所剩不多了,于是开到服务区加油,加满油后又开始匀速行驶,下面哪一幅图可以近似的刻画该汽车在这段时间内的速度变化情况( )
A. B. C. D.
2.如图,有两条相互垂直的卡槽,一小哥将一根木棒的两端分别卡在卡槽中,在木棒的中部插有一支记号笔,接着移动木棒的一端,另一端也随之移动.我们惊讶地发现:记号笔画出了一段圆弧!根据你所学的有关直角三角形的知识,分析“木棒作弧”中所运用的数学道理是( )
A.直角三角形的两直角边长度的平方和等于第三边长度的平方
B.直角三角形的面积等于两直角边乘积的一半
C.直角三角形的两个锐角互余
D.直角三角形斜边上的中线等于斜边的一半
3.已知点在第二象限,且m为整数,则m的值是( )
A.0 B.1 C.2 D.3
4.在平面直角坐标系中,,,若点在直线上,且,则点M的坐标为( )
A. B.或 C. D.或
5.如图,在平面直角坐标系内,其中,.点B,C的坐标分别为,.将沿x轴向右平移,当点A在直线时,线段扫过的面积为( )
A.16 B.20 C.32 D.38
6.如图,在平面直角坐标系中,线段所在直线的解析式为,是的中点,P是上一动点,则的最小值是( )
A. B. C. D.
7.如图,,矩形ABCD在的内部,顶点A,B分别在射线OM,ON上,,,则点D到点O的最大距离是( )
A. B. C. D.
8.如图,已知矩形的边,,E为边上一点.将沿所在的直线翻折,点C恰好落在边上的点F处,过点F作,垂足为点M,取的中点N,连接,则的长为( )
A.3 B. C. D.
9.为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:
①这次调查属于全面调查
②这次调查共抽取了名学生
③这次调查阅读所用时间在的人数最少
④这次调查阅读所用时间在的人数占所调查人数的,其中正确的有( ).
A.②③④ B.①③④ C.①②④ D.①②③
10.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,,F是AB边上一点,将沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A. B. C.1 D.
11.如图,在平面直角坐标中,,,平分,点关于x轴的对称点是( )
A. B. C. D.
12.在“探索一次函数的系数k,b与图象的关系”活动中,老师给出了直角坐标系中的三个点:,,.同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式,,.分别计算,,的值,其中最大的值等于( )
A. B. C.5 D.4
13.如图,,,是内部的射线且,过点A作于点D,过点C作于点E,在上取点F,使得,连接.
设,,,给出下面三个结论:
①;
②;
③.
上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
参考答案
1.答案:B
解析:汽车经历:加速-匀速-减速到站-加速-匀速,
加速:速度增加,
匀速:速度保持不变,
减速:速度下降,
到站:速度为0.
观察四个选项的图象是否符合题干要求,只有B选项符合.
故选B.
2.答案:D
解析:因为“木棒作弧”过程中弧上的点到两条相互垂直的卡槽交点距离相等,且木棒作为三角形的斜边,记号笔在木棒的中点,
所以运用了直角三角形斜边上的中线等于斜边的一半,
故选:D.
3.答案:B
解析:点在第二象限,
,
解得:,
m为整数,
,
故选:B.
4.答案:B
解析:,,
与y轴平行,A、B两点的横坐标相同,又,
,点M在直线上,
,
M点纵坐标为:或,
M点的坐标为:或,
故选:B.
5.答案:B
解析:点B,C的坐标分别为,
,.
当点A落在直线时,
解得
平移后点B(7,0)
平移了个单位
线段扫过的面积为
故选B.
6.答案:C
解析:作点B关于的对称点,连接交于,
此时,的值最小,最小值为的长,
线段所在直线的解析式为,
,,
,,
是的中点,
,
是点B关于的对称点,
,,,
四边形是正方形,
,
的最小值是.
故选:C.
7.答案:B
解析:取AB中点E,连接OE、DE、OD,
,
.
在中,利用勾股定理可得.
在中,根据三角形三边关系可知,
当O、E、D点共线时,OD最大为.
故选:B.
8.答案:D
解析:如图所示连接,.
由翻折的性质可知,垂直平分线段,
,
又,
F,M,C共线,
,
四边形是矩形,
,
,
N是的中点,M是的中点,
是的中位线,
.
故选:D.
9.答案:A
解析:这次调查属于抽样调查,故①错误;
结合频数分布直方图,可计算得共抽取名学生,故②正确;
结合频数分布直方图,阅读所用时间在的共8名学生,人数最少,故③正确;
这次调查阅读所用时间在的人数占比为,即,故④正确;
故选:A.
10.答案:B
解析:四边形是边长为4的正方形,
,,
,
由翻折得,,垂直平分,
在和中,
,
,
,
,
,
,
,且,
,
解得,
,
,
解得,
故选:B.
11.答案:C
解析:如图,过B点作轴于点C,则,
,
平分,
,
又,
,
,即,,
,
关于x轴的对称点的坐标为,
故选:C.
12.答案:B
解析:不妨设直线的函数表达式为,直线的函数表达式为,直线的函数表达式为,
将,代入得:,
解得:,
.
同理,可求出,,
,.
又,
其中最大的值等于.
故选:B.
13.答案:B
解析:,,
,
,
,,
,
在和中,
,
,
,,
,
,
,故①正确,
连接,则,
,,
,
,
,故②错误,
是内部的射线且,
,
,
,
,故③正确.
故选:B.
同课章节目录
