2024成都中考数学三轮冲刺:相似、面积、动点综合题预测精选(PDF版,含答案)
文档属性
| 名称 | 2024成都中考数学三轮冲刺:相似、面积、动点综合题预测精选(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 19:25:51 | ||
图片预览



文档简介
2024成都中考数学相似、面积、动点综合题预测精选
一.解答题(共 11 小题)
1.(2022 苏州)(1)如图 1,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交 AB于点 D,DE∥AC,交
BC于点 E.
①若 DE=1,BD= ,求 BC的长;
②试探究 ﹣ 是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)如图 2,∠CBG和∠BCF是△ABC的 2个外角,∠BCF=2∠CBG,CD平分∠BCF,交 AB的延
长线于点 D,DE∥AC,交 CB的延长线于点 E.记△ACD的面积为 S1,△CDE的面积为 S2,△BDE
的面积为 S3.若 S1 S3= ,求 cos∠CBD的值.
第 1页(共 39页)
2.(2021 苏州)如图,在矩形 ABCD中,线段 EF、GH分别平行于 AD、AB,它们相交于点 P,点 P1、
P2分别在线段 PF、PH上,PP1=PG,PP2=PE,连接 P1H、P2F,P1H与 P2F相交于点 Q.已知 AG:
GD=AE:EB=1:2,设 AG=a,AE=b.
(1)四边形 EBHP的面积 四边形 GPFD的面积(填“>”、“=”或“<”)
(2)求证:△P1FQ∽△P2HQ;
(3)设四边形 PP1QP2的面积为 S1,四边形 CFQH的面积为 S2,求 的值.
第 2页(共 39页)
3.(2024 姑苏区一模)(1)如图①,△ABC中,AB=AC=10,BC=12,D为边 BC上一动点,将点 A
绕点 D按顺时针方向旋转,得到点 A′,使得∠ADA′=∠B,过点 C作 AD的平行线,交直线 DA′
于点 E,连接 AE.
①若 BD=2,求 AD的长度;
②求 AD CE的最大值.
(2)如图②,当点 D在 BC的延长线上时,将点 A绕点 D按顺时针方向旋转,得到点 A′,使得∠
ADA′=∠B,过点 C作 AD的平行线,交直线 DA′于点 E,连接 AE.记△ABD的面积为 S1,△ADE
的面积为 S2,△CDE的面积为 S3,若 ,求 sin∠ADB的值.
第 3页(共 39页)
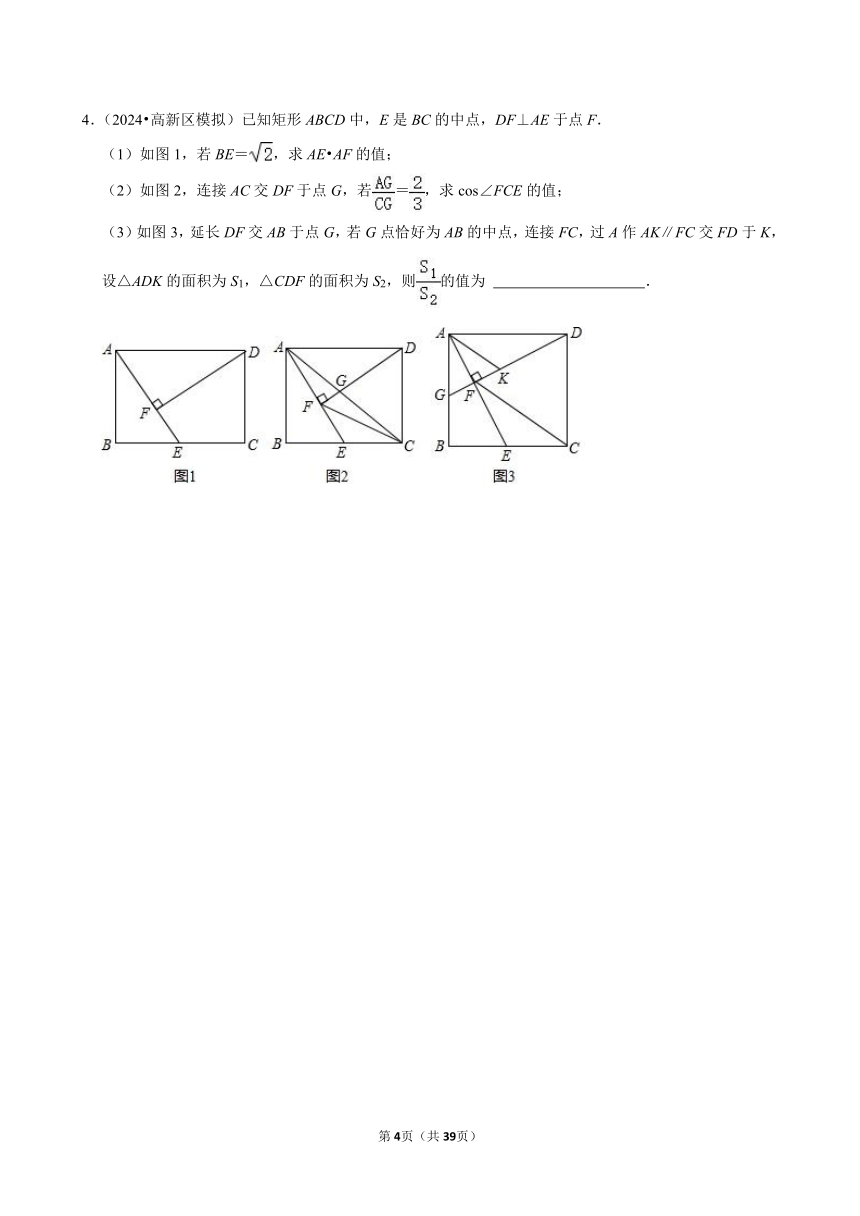
4.(2024 高新区模拟)已知矩形 ABCD中,E是 BC的中点,DF⊥AE于点 F.
(1)如图 1,若 BE= ,求 AE AF的值;
(2)如图 2,连接 AC交 DF于点 G,若 = ,求 cos∠FCE的值;
(3)如图 3,延长 DF交 AB于点 G,若 G点恰好为 AB的中点,连接 FC,过 A作 AK∥FC交 FD于 K,
设△ADK的面积为 S1,△CDF的面积为 S2,则 的值为 .
第 4页(共 39页)
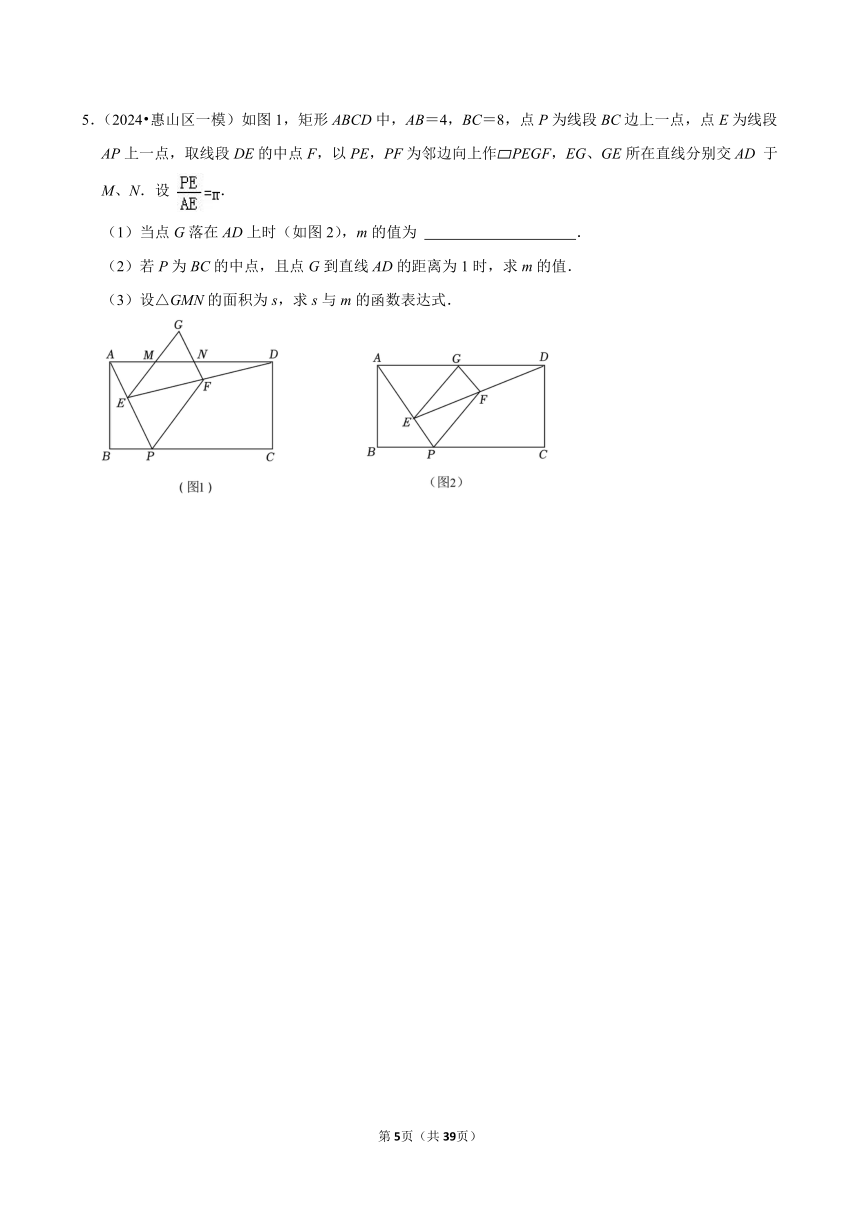
5.(2024 惠山区一模)如图 1,矩形 ABCD中,AB=4,BC=8,点 P为线段 BC边上一点,点 E为线段
AP上一点,取线段 DE的中点 F,以 PE,PF为邻边向上作 PEGF,EG、GE所在直线分别交 AD 于
M、N.设 .
(1)当点 G落在 AD上时(如图 2),m的值为 .
(2)若 P为 BC的中点,且点 G到直线 AD的距离为 1时,求 m的值.
(3)设△GMN的面积为 s,求 s与 m的函数表达式.
第 5页(共 39页)
6.(2023 吉安县模拟)课本再现
如图 1,在等边△ABC中,E为边 AC上一点,D为 BC上一点,且 AE=CD,连接 AD与 BE相交于点
F.
(1)AD与 BE的数量关系是 ,AD与 BE构成的锐角夹角∠BFD的度数是 ;
深入探究
(2)将图 1中的 AD延长至点 G,使 FG=BF,连接 BG,CG,如图 2所示.求证:GA平分∠BGC.(第
一问的结论,本问可直接使用)
迁移应用
(3)如图 3,在等腰△ABC中,AB=AC,D,E分别是边 BC,AC上的点,AD与 BE相交于点 F.若
∠BAC=∠BFD,且 BF=3AF,求 值.
第 6页(共 39页)
7.(2023 苏州模拟)如图①,点 E为矩形 ABCD中较短边 AB上一任意点,连接 DE,在 AD上方以 DE
为边作正方形 DEFG,分别连接 CE、CF、CG,F与 BC交于点 H,若△ECD的面积 y1与 BE的长度 x
的函数关系的图象如图②中直线的一部分,正方形 DEFG的面积 y2与 BE的长度 x的函数关系的图象
如图②中抛物线的一部分.
(1)①矩形 ABCD的面积= ;
②求出矩形 ABCD的周长;
(2)E、C、G三点能否共线,若能,求出此时 x的值,若不能,请说明理由;
(3)连接 FB,令△BFE的面积为 S1,△CEF的面积为 S2,当 x为间值时, 取得最大值?此时∠FCB
和∠CGD是否相等?请说明理由.
第 7页(共 39页)
8.(2023 工业园区一模)如图①,在四边形 ABCD中,AD∥BC,∠ABC=90°,AD=3,BC=5, .点
P在 AB上,连接 BD、PC、PD.
(1)求 AB的长;
(2)探索:是否存在这样的点 P,使得 PC平分∠BCD、PD平分∠ADB同时成立?若存在,求出 PA
的长;若不存在,说明理由;
(3)如图②,PC与 BD相交于点 E,过点 P作 PF∥CD,PF与 BD相交于点 F.设△PEF、△PCD
的面积分别为 S1、S2.若 S2=6S1,求 PA的长.
第 8页(共 39页)
9.(2023 涟水县二模)如图,△ABC是边长为 3的等边三角形,D是 AB上一动点,连接 CD,以 CD为
边向 CD的右侧作等边三角形 CDE,连接 AE.
(1)【尝试初探】
如图 1,当点 D在线段 AB上运动时,AC,DE相交于点 F,在运动过程中发现有两个三角形始终保持
全等,请你找出这对全等三角形,并说明理由.
(2)【深入探究】
如图 2,当点 D在线段 AB上运动时,延长 ED,交 CB的延长线于点 H,随着 D点位置的变化,H点
的位置随之发生变化,当 AD=2BD时,求 tan∠DHC的值.
(3)【拓展延伸】
如图 3,当点 D在 BA的延长线上运动时,CD,AE相交于点 F,设△ADF的面积为 S1,△CEF的面积
为 S2,当 S2=4S1时,求 BD的长.
第 9页(共 39页)
10.(2021 吴江区模拟)如图,以△ABC的边 AB为直径的⊙O与边 AC相交于点 D,BC是⊙O的切线,
E为 BC的中点,连接 AE、DE.
(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形 ABED的面积为 S2.若 S2=5S1,求 tan∠BAC的值;
(3)在(2)的条件下,若 AE=3 ,求⊙O的半径长.
第 10页(共 39页)
11.(2020 工业园区一模)【探索规律】
如图①,在△ABC 中,点 D,E,F分别在 AB,BC,AC上,且 DF∥BC,EF∥AB.设△ADF的边
DF上的高为 h1,△EFC的边 CE上的高为 h2.
(1)若△ADF、△EFC的面积分别为 3,1,则 = ;
(2)设△ADF、△EFC、四边形 BDFE的面积分别为 S1,S2,S,求证:S=2 ;
【解决问题】
(3)如图②,在△ABC中,点 D,E分别在 AB,AC上,点 F,G在 BC上,且 DE∥BC,DF∥EG.若
△ADE、△DBF、△EGC的面积分别为 3,7,5,求△ABC的面积.
第 11页(共 39页)
参考答案与试题解析
一.解答题(共 11 小题)
1.【解答】解:(1)①∵CD平分∠ACB,
∴∠ACD=∠DCB= ∠ACB,
∵∠ACB=2∠B,
∴∠ACD=∠DCB=∠B,
∴CD=BD= ,
∵DE∥AC,
∴∠ACD=∠EDC,
∴∠EDC=∠DCB=∠B,
∴CE=DE=1,
∴△CED∽△CDB,
∴ ,
∴ ,
∴BC= ;
② ﹣ 是定值.
∵DE∥AC,
∴ ,
同①可得,CE=DE,
∴ ,
∴ =1,
∴ ﹣ 是定值,定值为 1;
(2)∵DE∥AC,
第 12页(共 39页)
∴ ,
∵ ,
∴ ,
又∵S1 S3= ,
∴ ,
设 BC=9x,则 CE=16x,
∵CD平分∠BCF,
∴∠ECD=∠FCD= ∠BCF,
∵∠BCF=2∠CBG,
∴∠ECD=∠FCD=∠CBD,
∴BD=CD,
∵DE∥AC,
∴∠EDC=∠FCD,
∴∠EDC=∠CBD=∠ECD,
∴CE=DE,
∵∠DCB=∠ECD,
∴△CDB∽△CED,
∴ ,
∴CD2=CB CE=144x2,
∴CD=12x,
过点 D作 DH⊥BC于点 H,
第 13页(共 39页)
∵BD=CD=12x,
∴BH= BC= x,
∴cos .
2.【解答】解:(1)∵四边形 ABCD为矩形,
∴∠A=∠B=∠C=90°,
∵GH∥AB,
∴∠B=∠GHC=90°,∠A=∠PGD=90°,
∵EF∥AD,
∴∠PGD=∠HPF=90°,
∴四边形 PFCH为矩形,
同理可得,四边形 AGPE、GDFP、EPHB均为矩形,
∵AG=a,AE=b,AG:GD=AE:EB=1:2,
∴PE=a,PG=b,GD=PF=2a,EB=PH=2b,
∴四边形 EBHP的面积=PE PH=2ab,四边形 GPFD的面积=PG PF=2ab,
故答案为:=;
(2)∵PP1=PG,PP2=PE,
由(1)知 PE PH=2ab,PG PF=2ab,
∴PP2 PH=PP1 PF,
即 = ,
又∵∠FPP2=∠HPP1,
∴△PP2F∽△PP1H,
第 14页(共 39页)
∴∠PFP2=∠PHP1,
∵∠P1QF=∠P2QH,
∴△P1FQ∽△P2HQ;
(3)连接 P1P2、FH,
∵ = = , = = ,
∴ = ,
∵∠P1PP2=∠C=90°,
∴△PP1P2∽△CFH,
∴ = = , =( )2= ,
由(2)中△P1FQ∽△P2HQ,得 = ,
∴ = ,
∵∠P1QP2=∠FQH,
∴△P1QP2∽△FQH,
∴ =( )2= ,
∵S1= + ,S2=S△CFH+S△FQH,
∴S1= S△CFH+ S△FQH= S2,
∴ = .
第 15页(共 39页)
3.【解答】解:(1)①如图 1,
作 AF⊥BC于 F,作 DG⊥AB于 G,
∴∠BGD=∠AFB=90°,
∵AB=AC=10,
∴BF=CF= BC=6,
∴AF=8,
∵∠B=∠B,
∴△BDG∽△BAF,
∴ ,
∴ ,
∴DG= ,BG= ,
∴AG=AB﹣BG=10﹣ = ,
∴AD= =4 ;
第 16页(共 39页)
②∵CE∥AD,
∴∠DEC=∠ADA′,
∵∠ADA′=∠B,
∴∠CED=∠B,
∵∠BAD+∠ADB=180°﹣∠B,∠ADB+∠CDE=180°﹣∠ADA′,
∴∠BAD=∠CDE,
∴△ABD∽△DEC,
∴ ,
∴AD CE=BD CD=BD (12﹣BD)=﹣(BD﹣6)2+36,
∴当 BD=6时,(AD BD)最大=36;
(2)如图 2,
作 AF⊥BD于 F,设 CD=x,
∵DF=CF+CD=x+6,AF=8,
∴AD2+82+(x+6)2=x2+12x+100,
∵CE∥AD,
∴S△ADE=S△ACD,∠CED=∠ADA′,∠ADB=∠DCE,
∵∠B=∠ADA′,
∴∠CED=∠B,
∴△CDE∽△DAB,
∴ = ,
第 17页(共 39页)
∴S△CDE= S△ABD,
∵ ,
∴ = ,
∵ ,
∴ = ,
∴x2=38,x2=﹣2(舍去),
∴CD=38,DF=38+6=44,
∴AD= =20 ,
∴sin∠ADB= .
4.【解答】解:(1)∵E是 BC的中点,
∴BC=2BE=2 ,
∵四边形 ABCD是矩形,
∴AD=BC=2 ,∠B=90°,AD∥BC,
∴∠AEB=∠DAF,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ABE∽△DFA,
∴ = ,
∴AE AF=AD BE=2 × =4;
(2)延长 DE交 CB的延长线于 H,连接 DE、AH,如图 2所示:
∵四边形 ABCD是矩形,
∴AD∥BC,AD=BC,∠BCD=90°,
∴△ADG∽△CHG,
第 18页(共 39页)
∴ = = ,
∴BH= BC,
∵E是 BC的中点,
∴BE=CE=BH,
∴EH=BC=AD,
∴四边形 ADEH是平行四边形,
∵DF⊥AE,
∴四边形 ADEH是菱形,
∴DF=HF,∠AEH=∠AED,DE=AD=EH=BC,
∴CE= DE,
∴∠CDE=30°,
∴∠CED=90°﹣30°=60°,
∴∠AEH=∠AED=60°,
∵DF⊥AE,
∴∠FDE=30°=∠CDE,
∴FE=CE,
∴∠FCE=∠CFE= ∠AEH=30°,
∴cos∠FCE= ;
(3)过 F作 PQ⊥AB于 P,交 CD于 Q,作 KH⊥AD于 H,如图 3所示:
则 PQ=AD,AP=DQ,PQ∥BC∥AD,
∵G是 AB的中点,E是 BC的中点,
∴AB=2AG,BC=2BE,
∵四边形 ABCD是矩形,
∴AD=BC,AB=CD,∠B=∠DAG=90°,
∵DF⊥AE,
∴∠ADF+∠DAF=∠BAE+∠DAF=90°,
∴∠BAE=∠ADF,
∴△ABE∽△DAG,
第 19页(共 39页)
∴ = ,
∴AB AG=AD BE,即 AB2= AD2,
∴AB=AD,
∴四边形 ABCD是正方形,
∴AB=BC=CD=AD=PQ,
设 AB=BC=CD=AD=PQ=4a,
则 BE=AG=2a,
∴tan∠ADG=tan∠BAE= = ,AE=DG= =2 a,
∵DF⊥AE,
∴AF= = = a,
∵PQ∥BC,
∴△APF∽△ABE,
∴ = = ,即 = = ,
解得:AP= a,PF= a,
∴CQ=PB=AB﹣AP=4a﹣ a= a,
FQ=PQ﹣PF=4a﹣ a= a,
∵KH⊥AD,
∴tan∠ADG= = ,
设 KH=x,则 DH=2x,
∵PQ∥AD,AK∥FC,
∴∠DAF=∠QFE,∠KAF=∠CFE,
∴∠DAK=∠QFC,
又∵∠AHK=∠FQC=90°,
∴△AHK∽△FQC,
∴ = ,即 = ,
第 20页(共 39页)
解得:AH= x,
∵AH+DH=AD,
∴ x+2x=4a,
解得:x= a,
∴KH= a,
∵△ADK的面积为 S1= AD×KH,△CDF的面积为 S2= CD×FQ,
∴ = = = ;
故答案为: .
5.【解答】解:(1)∵四边形 PEGF是平行四边形,
∴GF=PE,GF∥PE,
∴△DGF∽△DAE,
∴ ,
∵F是 DE的中点,
∴DF= DE,
∴ ,
第 21页(共 39页)
∴AE=2GF,
∴ ,
∴m= ,
故答案为: ;
(2)如图 1,
当点 G在矩形 ABCD的外部时,
作 GH⊥AD于 H,作射线 DG,交 PA的延长线于 W,作 WQ⊥PA,交 PA的延长线于点 Q,
由(1)得,
G是 DW的中点,
同理可得 WQ=2GH=2,PE=FG= WE,
设 PE=FG=x,则 WE=2x,
∵四边形 ABCD是矩形,
∴∠DAB=∠B=90°,
∵P时 BC的中点,
∴PB= BC=4,
∴AB=PB,
∴∠WAQ=∠DAP=∠PAB=45°,
∴AW= WQ=2 ,AP= AB=4 ,
∴WP=AW+AP=6 ,
由 WE+PE=WP得,
2x+x=6 ,
∴x=2 ,
第 22页(共 39页)
∴PE=2 ,
∴AE=AP﹣PE=2 ,
∴m=1,
如图 2,
当点 G在矩形 ABCD的内部时,
由上可知:AW=2 ,
∴PW=AP﹣﹣AW=2 ,
∴PE= PW= ,
∴AE=4 = ,
∴m= ,
综上所述:m=1或 ;
(3)如图 3,
当 m< 时,
延长 EP至 X,使 PX=EP,连接 DP,DX,
∵点 F是 DE的中点,
∴PF∥DX,
第 23页(共 39页)
∵EM∥PF,
∴EM∥DX,
∴∠AME=∠ADX,
∵GF∥PE,
∴∠MNG=∠DAX,
∴△MNG∽△DAX,
∴ ,
∵S△ADP= AD AB= , ,
∴S△DPX=S△DEP= S△ADP= ,
∴S△ADX=S△ADP+S△DPX=16+ = ,
设 AE=x,则 GF=PE=mx,
∵FN= AE= x,
∴NG=FN﹣GF= ,
∵AX=AE+PE+PX=x+2mx=(1+2m)x,
∴ =( )2,
∴S= ,
如图 4,
第 24页(共 39页)
当 m> 时,
同理可得,
,NG=FG﹣NF=(m﹣ )x,AX=(1+2m)x,
∴S= ,
综上所述:S= .
6.【解答】(1)解:∵△ABC是等边三角形,
∴AB=CA,∠BAE=∠C=60°,
在△ACD和△BAE中,
,
∴△ACD≌△BAE(SAS).
∴AD=BE,∠CAD=∠ABE,
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,
故答案为:AD=BE,60°;
(2)证明:由(1)可知,∠BFD=60°,
∴∠AFB=120°,
∵FG=BF,
∴△BFG是等边三角形,
∴BF=BG,∠FBG=∠BGF=60°,
第 25页(共 39页)
∵△ABC是等边三角形,
∴AB=CB,∠ABC=60°,
∴∠ABC=∠FBG,
∴∠ABC﹣∠FBD=∠FBG﹣∠FBD,
即∠ABF=∠CBG,
∴△ABF≌△CBG(SAS),
∴∠AFB=∠CGB=120°,
∴∠CGF=∠CGB﹣∠BGF=120°﹣60°=60°,
∴∠BGF=∠CGF,
∴GA平分∠BGC;
(3)解:如图 3,延长 FD至点 G,使 FG=BF,连接 BG、CG,过点 D作 DM⊥BG于点 M,DN⊥CG
于点 N,
∵AB=AC,FG=BF,
∴ = ,
∵∠BAC=∠BFD,
∴△ABC∽△FBG,
∴ = ,∠ABC=∠FBG,
∴∠ABC﹣∠CBE=∠FBG﹣∠CBE,
即∠ABF=∠CBG,
∴△ABF∽△CBG,
∴ = =3,∠BAF=∠BCG,
∵∠ADB=∠CDG,
∴∠CGD=∠ABD,
∵AB=AC,FG=BF,
第 26页(共 39页)
∴∠ABC=∠ACB,∠FBG=∠FGB,
∵∠BAC=∠BFD,
∴∠BAC=∠FGB,
∴∠CGD=∠FGB,
∴DG平分∠BGC,
∵DM⊥BG,DN⊥CG,
∴DM=DN,
∵S△BGD= BG DM,S△CGD= CG DN,
∴ = = =3,
又∵ = ,
∴ =3.
方法二:如图 4,过点 D作 DP∥AB交 AC于点 P,
则∠BAF=∠ADP,∠ABC=∠PDC,
∵∠BAC=∠BFD,∠BFD=∠ABF+∠BAF,∠BAC=∠BAF+∠DAP,
∴∠ABF=∠DAP,
∴△ABF∽△DAP,
∴ = ,
即 = =3,
∵AB=AC,
∴∠ABC=∠ACB=∠PDC,
∴PD=PC,
第 27页(共 39页)
∵DP∥AB,
∴ = = =3.
7.【解答】解:(1)①由图②知,△ECD的面积为 6,
∴ CD AD=6,
∴CD AD=12,
∴矩形 ABCD的面积为 12;
故答案为:12;
②由图②知,正方形 DEFG的面积最大为 25,此时边 DE最大,E与 B重合,
∴AB2+AD2=25,
由矩形 ABCD,结合①可知 AB AD=CD AD=12,
∴AB+AD= = =7,
∴矩形 ABCD的周长为 14;
(2)E、C、G三点不能共线,理由如下:
由(1)知 AB+AD=7,AB AD=12,
∴AB=3,AD=4(AB为矩形 ABCD的较短边,AB=4,AD=3已舍去),
以 A为原点,AD所在直线为 x轴建立直角坐标系,过 G作 GK⊥CD交 DC延长线于 K,如图:
∵∠KDG=90°﹣∠EDC=∠EDA,∠K=90°=∠EAD,DE=DG,
∴△DKG≌△DAE(AAS),
∴DK=AD=4,KG=AE,
设 AE=m,则 KG=m,
∴E(0,m),G(4+m,4),
第 28页(共 39页)
∴直线 EG函数表达式为 y= x+m,
若 C(4,3)在直线 EG上,则 3= ×4+m,
变形整理得:m2﹣3m+4=0,
∵Δ=(﹣3)2﹣4×4=﹣7<0,
∴C(4,3)不可能满足 y= x+m,
∴C不可能在直线 EG上,故 E、C、G三点不能共线;
(3)过 F作 FT⊥y轴于 T,FW⊥BC于 W,如图:
∵∠TEF=90°﹣∠AED=∠ADE,∠ETF=90°=∠EAD,EF=ED,
∴△EFT≌△DEA(AAS),
∴TF=AE,TE=AD=4,
∵BE=x,
∴AE=AB﹣BE=3﹣x=TF,
∵BH∥TF,
∴ = 即 = ,
∴BH=﹣ + x,
∴CH=4﹣BH= ﹣ x+4,
∴S1= BE TF= x (3﹣x)=﹣ x2+ x,S2= CH TE= ( ﹣ x+4)×4= ﹣ x+8,
∴ = =﹣1+ ,
第 29页(共 39页)
当 x2﹣3x+16最小时, 最大,从而 最大,
∵x2﹣3x+16=(x﹣ )2+ ,
∴当 x= 时,x2﹣3x+16最小为 ,此时 取得最大值,
∴BE= ,
∴AE=TF=3﹣ = ,TB=TE﹣BE=4﹣ = ,
∴BW=TF= ,FW=TB= ,
∴CW=BC﹣BW=4﹣ = ,
∴CW=FW,
∴△CFW是等腰直角三角形,
∴∠FCB=45°,
∵∠EGD=45°,
∴∠FCB=∠EGD,
由(2)知 C不在 EG上,
∴∠CGD≠∠FCB.
∴当 x= 时, 取得最大值,此时∠FCB与∠CGD不相等.
8.【解答】解:(1)如图 1,过 D作 DM⊥BC于 M,则四边形 ABMD是矩形,
∴AB=DM,BM=AD=3(矩形性质),
∴CM=BC﹣BM=2,
在 Rt△CDM中,
由勾股定理得 ,
第 30页(共 39页)
∴AB=4,
∴AB的长为 4;
(2)不存在,理由如下:
如图 2,过 P作 PH∥AD交 BD于 G,交 CD于 H,
∴PH∥AD∥BC,
∴∠ADP=∠DPG,∠HPC=∠BCP(两直线平行,内错角相等),
∠GHD=∠BCD(两直线平行,同位角相等),
∵PC平分∠BCD,
∴∠ADP=∠PDG(角平分线的性质),
∴∠DPG=∠PDG,
∴PG=DG(等角对等边),
在 Rt△ABD中, ,
由勾股定理得 ,
∴BD=BC,
∴∠BDC=∠BCD,
∴∠GHD=∠BDC,
∴DG=GH,
∴PG=DG=GH,
设 PG=DG=GH=a,则 BG=5﹣a, ,
∵∠PBG=∠ABD,∠BPG=∠A=90°,
∴△PBG∽△ABD,
∴ ,
即 ,
第 31页(共 39页)
解得 ,
∴ ,
∵GH∥BC,
∴△DGH∽△DBC,
∴ ,即 ,
解得 ,
∴ ,
若 PD平分∠ADB,则∠BCP=∠HCP=∠HPC,即 PH=CH,
∵ ,与 PH=CH矛盾,
∴不存在这样的点 P,使得 PC平分∠BCD、PD平分∠ADB同时成立;
(3)令△PEF中 PE边上的高为 h1,△PCD中 PC边上的高为 h2,
∵PF∥CD,
∴∠PFE=∠CDE,∠FPE=∠DCE,
∴△PFE∽△CDE,
设 ,则 ,
∴PE=kCE,h1=kh2,
∴ ,
,
∵S2=6S1,即 ,
整理得 6k2﹣k﹣1=0,则(2k﹣1)(3k+1)=0,
解得 , (舍去),
∴ ,
如图 3,过 E作 EQ∥AD交 AB于 Q,
第 32页(共 39页)
∴QE∥BC,
∴△PQE∽△PBC,
∴ ,
即 ,
∴ , ,
∵QE∥AD,
∴△BEQ∽△BDA,
∴ ,即 ,
解得 ,
∴ ,
∴ ,
∴AP的长为 .
9.【解答】解:(1)如图 1,△BCD≌△ACE,理由如下:
∵△ABC与△CDE都是等边三角形,
∴BC=AC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE(SAS);
(2)如图 2,过点 D作 DG⊥BC于 D点 G,
第 33页(共 39页)
∵△ABC是边长为 3的等边三角形,AD=2BD,
∴∠ABC=∠ACB=60°,BD=1,AD=2,
∵DG⊥BC,
∴BG= ,
DG= BG= ,
由(1)得,△BCD≌△ACE,
∴AE=BD=1,∠CAE=∠CBA=60°,
∴∠CAE=∠ACB,
∴AE∥CH,
∴△ADE∽△BDH,
∴ ,
∵AD=2BD,AE=1,
∴ ,
∴BH= ,
∴GH=BH+BG=1,
∵DG⊥BC,
∴tan∠DHC= ;
(3)如图 3,过点 C作 CH⊥AB于点 H,
∵△ABC与△CDE都是等边三角形,
∴BC=AC,DC=EC,
第 34页(共 39页)
∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE(SAS),
∴∠BDC=∠AEC,
又∵∠AFD=∠CFE,
∴△AFD∽△CFE,
∴ ,
∵S2=4S1,
∴CE=2AD,
设 BD=x,
则 AD=BD﹣AB=x﹣3,
CD=CE=2(x﹣3)=2x﹣6,
∵CH⊥AB,△ABC是边长为 3的等边三角形,
∴AH= ,
CH= AH= ,
∴DH=AH+AD= ,
∵CH⊥AB,
∴CH2+DH2=CD2,
即( ) =(2x﹣6)2,
解得 x= ,
∵点 D在 BA的延长线上,
∴BD>AB,
∴x>3,
第 35页(共 39页)
∴x= ,
即 BD= .
10.【解答】(1)证明:连接 OD,
∴OD=OB
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为 BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵BC是以 AB为直径的⊙O的切线,
∴AB⊥BC,
∴∠EBO=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)∵S2=5 S1
∴S△ADB=2S△CDB
∴
∵△BDC∽△ADB
∴
∴DB2=AD DC
第 36页(共 39页)
∴ =
∴tan∠BAC= = .
(3)∵tan∠BAC= =
∴ = ,得 BC= AB
∵E为 BC的中点
∴BE= AB
∵AE=3 ,
∴在 Rt△AEB中,由勾股定理得
,解得 AB=4
故⊙O的半径 R= AB=2.
11.【解答】解:(1)∵DF∥BC,EF∥AB,
∴∠AFD=∠ACB,∠DAF=∠EFC,
∴△ADF∽△FEC,
∵△ADF、△EFC的面积分别为 3,1,
∴ ,
∴ ,
∵△ADF的边 DF上的高为 h1,△EFC的边 CE上的高为 h2,
∴ ;
故答案为: .
(2)证明:如图①,设 AD=a,BD=b,DB与 EF间的距离为 h,
第 37页(共 39页)
∵EF∥AB,DF∥BC,
∴四边形 DBFE是平行四边形,
∴BD=EF=b,
由(1)知△ADF∽△FEC,
∴ ,
∵S1= ah,
∴S2= ,
∴S1S2= ,
∴bh=2 ,
∵S=bh,
∴S=2 .
(3)如图②,过点 D作 DM∥AC交 BC于点 M,
∴∠DMF=∠ECG,
∵DE∥BC,DF∥EG,
第 38页(共 39页)
∴四边形 DFGE为平行四边形,
∴DF=EG,∠DFM=∠EGC,
∴△DFM≌△EGC(AAS),
∴S△DFM=S△EGC=5,
∵S△DBF=7,
∴S△BDM=7+5=12,
∵DE∥BM,DM∥AC,
∴∠ADE=∠DBM,∠BDM=∠BAE,
∴△DAE∽△BDM,
∴ = ,
∴ ,
∴ ,
同理,△ADE∽△ABC,
∴S△ABC=9S△ADE=9×3=27.
第 39页(共 39页)
一.解答题(共 11 小题)
1.(2022 苏州)(1)如图 1,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交 AB于点 D,DE∥AC,交
BC于点 E.
①若 DE=1,BD= ,求 BC的长;
②试探究 ﹣ 是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)如图 2,∠CBG和∠BCF是△ABC的 2个外角,∠BCF=2∠CBG,CD平分∠BCF,交 AB的延
长线于点 D,DE∥AC,交 CB的延长线于点 E.记△ACD的面积为 S1,△CDE的面积为 S2,△BDE
的面积为 S3.若 S1 S3= ,求 cos∠CBD的值.
第 1页(共 39页)
2.(2021 苏州)如图,在矩形 ABCD中,线段 EF、GH分别平行于 AD、AB,它们相交于点 P,点 P1、
P2分别在线段 PF、PH上,PP1=PG,PP2=PE,连接 P1H、P2F,P1H与 P2F相交于点 Q.已知 AG:
GD=AE:EB=1:2,设 AG=a,AE=b.
(1)四边形 EBHP的面积 四边形 GPFD的面积(填“>”、“=”或“<”)
(2)求证:△P1FQ∽△P2HQ;
(3)设四边形 PP1QP2的面积为 S1,四边形 CFQH的面积为 S2,求 的值.
第 2页(共 39页)
3.(2024 姑苏区一模)(1)如图①,△ABC中,AB=AC=10,BC=12,D为边 BC上一动点,将点 A
绕点 D按顺时针方向旋转,得到点 A′,使得∠ADA′=∠B,过点 C作 AD的平行线,交直线 DA′
于点 E,连接 AE.
①若 BD=2,求 AD的长度;
②求 AD CE的最大值.
(2)如图②,当点 D在 BC的延长线上时,将点 A绕点 D按顺时针方向旋转,得到点 A′,使得∠
ADA′=∠B,过点 C作 AD的平行线,交直线 DA′于点 E,连接 AE.记△ABD的面积为 S1,△ADE
的面积为 S2,△CDE的面积为 S3,若 ,求 sin∠ADB的值.
第 3页(共 39页)
4.(2024 高新区模拟)已知矩形 ABCD中,E是 BC的中点,DF⊥AE于点 F.
(1)如图 1,若 BE= ,求 AE AF的值;
(2)如图 2,连接 AC交 DF于点 G,若 = ,求 cos∠FCE的值;
(3)如图 3,延长 DF交 AB于点 G,若 G点恰好为 AB的中点,连接 FC,过 A作 AK∥FC交 FD于 K,
设△ADK的面积为 S1,△CDF的面积为 S2,则 的值为 .
第 4页(共 39页)
5.(2024 惠山区一模)如图 1,矩形 ABCD中,AB=4,BC=8,点 P为线段 BC边上一点,点 E为线段
AP上一点,取线段 DE的中点 F,以 PE,PF为邻边向上作 PEGF,EG、GE所在直线分别交 AD 于
M、N.设 .
(1)当点 G落在 AD上时(如图 2),m的值为 .
(2)若 P为 BC的中点,且点 G到直线 AD的距离为 1时,求 m的值.
(3)设△GMN的面积为 s,求 s与 m的函数表达式.
第 5页(共 39页)
6.(2023 吉安县模拟)课本再现
如图 1,在等边△ABC中,E为边 AC上一点,D为 BC上一点,且 AE=CD,连接 AD与 BE相交于点
F.
(1)AD与 BE的数量关系是 ,AD与 BE构成的锐角夹角∠BFD的度数是 ;
深入探究
(2)将图 1中的 AD延长至点 G,使 FG=BF,连接 BG,CG,如图 2所示.求证:GA平分∠BGC.(第
一问的结论,本问可直接使用)
迁移应用
(3)如图 3,在等腰△ABC中,AB=AC,D,E分别是边 BC,AC上的点,AD与 BE相交于点 F.若
∠BAC=∠BFD,且 BF=3AF,求 值.
第 6页(共 39页)
7.(2023 苏州模拟)如图①,点 E为矩形 ABCD中较短边 AB上一任意点,连接 DE,在 AD上方以 DE
为边作正方形 DEFG,分别连接 CE、CF、CG,F与 BC交于点 H,若△ECD的面积 y1与 BE的长度 x
的函数关系的图象如图②中直线的一部分,正方形 DEFG的面积 y2与 BE的长度 x的函数关系的图象
如图②中抛物线的一部分.
(1)①矩形 ABCD的面积= ;
②求出矩形 ABCD的周长;
(2)E、C、G三点能否共线,若能,求出此时 x的值,若不能,请说明理由;
(3)连接 FB,令△BFE的面积为 S1,△CEF的面积为 S2,当 x为间值时, 取得最大值?此时∠FCB
和∠CGD是否相等?请说明理由.
第 7页(共 39页)
8.(2023 工业园区一模)如图①,在四边形 ABCD中,AD∥BC,∠ABC=90°,AD=3,BC=5, .点
P在 AB上,连接 BD、PC、PD.
(1)求 AB的长;
(2)探索:是否存在这样的点 P,使得 PC平分∠BCD、PD平分∠ADB同时成立?若存在,求出 PA
的长;若不存在,说明理由;
(3)如图②,PC与 BD相交于点 E,过点 P作 PF∥CD,PF与 BD相交于点 F.设△PEF、△PCD
的面积分别为 S1、S2.若 S2=6S1,求 PA的长.
第 8页(共 39页)
9.(2023 涟水县二模)如图,△ABC是边长为 3的等边三角形,D是 AB上一动点,连接 CD,以 CD为
边向 CD的右侧作等边三角形 CDE,连接 AE.
(1)【尝试初探】
如图 1,当点 D在线段 AB上运动时,AC,DE相交于点 F,在运动过程中发现有两个三角形始终保持
全等,请你找出这对全等三角形,并说明理由.
(2)【深入探究】
如图 2,当点 D在线段 AB上运动时,延长 ED,交 CB的延长线于点 H,随着 D点位置的变化,H点
的位置随之发生变化,当 AD=2BD时,求 tan∠DHC的值.
(3)【拓展延伸】
如图 3,当点 D在 BA的延长线上运动时,CD,AE相交于点 F,设△ADF的面积为 S1,△CEF的面积
为 S2,当 S2=4S1时,求 BD的长.
第 9页(共 39页)
10.(2021 吴江区模拟)如图,以△ABC的边 AB为直径的⊙O与边 AC相交于点 D,BC是⊙O的切线,
E为 BC的中点,连接 AE、DE.
(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形 ABED的面积为 S2.若 S2=5S1,求 tan∠BAC的值;
(3)在(2)的条件下,若 AE=3 ,求⊙O的半径长.
第 10页(共 39页)
11.(2020 工业园区一模)【探索规律】
如图①,在△ABC 中,点 D,E,F分别在 AB,BC,AC上,且 DF∥BC,EF∥AB.设△ADF的边
DF上的高为 h1,△EFC的边 CE上的高为 h2.
(1)若△ADF、△EFC的面积分别为 3,1,则 = ;
(2)设△ADF、△EFC、四边形 BDFE的面积分别为 S1,S2,S,求证:S=2 ;
【解决问题】
(3)如图②,在△ABC中,点 D,E分别在 AB,AC上,点 F,G在 BC上,且 DE∥BC,DF∥EG.若
△ADE、△DBF、△EGC的面积分别为 3,7,5,求△ABC的面积.
第 11页(共 39页)
参考答案与试题解析
一.解答题(共 11 小题)
1.【解答】解:(1)①∵CD平分∠ACB,
∴∠ACD=∠DCB= ∠ACB,
∵∠ACB=2∠B,
∴∠ACD=∠DCB=∠B,
∴CD=BD= ,
∵DE∥AC,
∴∠ACD=∠EDC,
∴∠EDC=∠DCB=∠B,
∴CE=DE=1,
∴△CED∽△CDB,
∴ ,
∴ ,
∴BC= ;
② ﹣ 是定值.
∵DE∥AC,
∴ ,
同①可得,CE=DE,
∴ ,
∴ =1,
∴ ﹣ 是定值,定值为 1;
(2)∵DE∥AC,
第 12页(共 39页)
∴ ,
∵ ,
∴ ,
又∵S1 S3= ,
∴ ,
设 BC=9x,则 CE=16x,
∵CD平分∠BCF,
∴∠ECD=∠FCD= ∠BCF,
∵∠BCF=2∠CBG,
∴∠ECD=∠FCD=∠CBD,
∴BD=CD,
∵DE∥AC,
∴∠EDC=∠FCD,
∴∠EDC=∠CBD=∠ECD,
∴CE=DE,
∵∠DCB=∠ECD,
∴△CDB∽△CED,
∴ ,
∴CD2=CB CE=144x2,
∴CD=12x,
过点 D作 DH⊥BC于点 H,
第 13页(共 39页)
∵BD=CD=12x,
∴BH= BC= x,
∴cos .
2.【解答】解:(1)∵四边形 ABCD为矩形,
∴∠A=∠B=∠C=90°,
∵GH∥AB,
∴∠B=∠GHC=90°,∠A=∠PGD=90°,
∵EF∥AD,
∴∠PGD=∠HPF=90°,
∴四边形 PFCH为矩形,
同理可得,四边形 AGPE、GDFP、EPHB均为矩形,
∵AG=a,AE=b,AG:GD=AE:EB=1:2,
∴PE=a,PG=b,GD=PF=2a,EB=PH=2b,
∴四边形 EBHP的面积=PE PH=2ab,四边形 GPFD的面积=PG PF=2ab,
故答案为:=;
(2)∵PP1=PG,PP2=PE,
由(1)知 PE PH=2ab,PG PF=2ab,
∴PP2 PH=PP1 PF,
即 = ,
又∵∠FPP2=∠HPP1,
∴△PP2F∽△PP1H,
第 14页(共 39页)
∴∠PFP2=∠PHP1,
∵∠P1QF=∠P2QH,
∴△P1FQ∽△P2HQ;
(3)连接 P1P2、FH,
∵ = = , = = ,
∴ = ,
∵∠P1PP2=∠C=90°,
∴△PP1P2∽△CFH,
∴ = = , =( )2= ,
由(2)中△P1FQ∽△P2HQ,得 = ,
∴ = ,
∵∠P1QP2=∠FQH,
∴△P1QP2∽△FQH,
∴ =( )2= ,
∵S1= + ,S2=S△CFH+S△FQH,
∴S1= S△CFH+ S△FQH= S2,
∴ = .
第 15页(共 39页)
3.【解答】解:(1)①如图 1,
作 AF⊥BC于 F,作 DG⊥AB于 G,
∴∠BGD=∠AFB=90°,
∵AB=AC=10,
∴BF=CF= BC=6,
∴AF=8,
∵∠B=∠B,
∴△BDG∽△BAF,
∴ ,
∴ ,
∴DG= ,BG= ,
∴AG=AB﹣BG=10﹣ = ,
∴AD= =4 ;
第 16页(共 39页)
②∵CE∥AD,
∴∠DEC=∠ADA′,
∵∠ADA′=∠B,
∴∠CED=∠B,
∵∠BAD+∠ADB=180°﹣∠B,∠ADB+∠CDE=180°﹣∠ADA′,
∴∠BAD=∠CDE,
∴△ABD∽△DEC,
∴ ,
∴AD CE=BD CD=BD (12﹣BD)=﹣(BD﹣6)2+36,
∴当 BD=6时,(AD BD)最大=36;
(2)如图 2,
作 AF⊥BD于 F,设 CD=x,
∵DF=CF+CD=x+6,AF=8,
∴AD2+82+(x+6)2=x2+12x+100,
∵CE∥AD,
∴S△ADE=S△ACD,∠CED=∠ADA′,∠ADB=∠DCE,
∵∠B=∠ADA′,
∴∠CED=∠B,
∴△CDE∽△DAB,
∴ = ,
第 17页(共 39页)
∴S△CDE= S△ABD,
∵ ,
∴ = ,
∵ ,
∴ = ,
∴x2=38,x2=﹣2(舍去),
∴CD=38,DF=38+6=44,
∴AD= =20 ,
∴sin∠ADB= .
4.【解答】解:(1)∵E是 BC的中点,
∴BC=2BE=2 ,
∵四边形 ABCD是矩形,
∴AD=BC=2 ,∠B=90°,AD∥BC,
∴∠AEB=∠DAF,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ABE∽△DFA,
∴ = ,
∴AE AF=AD BE=2 × =4;
(2)延长 DE交 CB的延长线于 H,连接 DE、AH,如图 2所示:
∵四边形 ABCD是矩形,
∴AD∥BC,AD=BC,∠BCD=90°,
∴△ADG∽△CHG,
第 18页(共 39页)
∴ = = ,
∴BH= BC,
∵E是 BC的中点,
∴BE=CE=BH,
∴EH=BC=AD,
∴四边形 ADEH是平行四边形,
∵DF⊥AE,
∴四边形 ADEH是菱形,
∴DF=HF,∠AEH=∠AED,DE=AD=EH=BC,
∴CE= DE,
∴∠CDE=30°,
∴∠CED=90°﹣30°=60°,
∴∠AEH=∠AED=60°,
∵DF⊥AE,
∴∠FDE=30°=∠CDE,
∴FE=CE,
∴∠FCE=∠CFE= ∠AEH=30°,
∴cos∠FCE= ;
(3)过 F作 PQ⊥AB于 P,交 CD于 Q,作 KH⊥AD于 H,如图 3所示:
则 PQ=AD,AP=DQ,PQ∥BC∥AD,
∵G是 AB的中点,E是 BC的中点,
∴AB=2AG,BC=2BE,
∵四边形 ABCD是矩形,
∴AD=BC,AB=CD,∠B=∠DAG=90°,
∵DF⊥AE,
∴∠ADF+∠DAF=∠BAE+∠DAF=90°,
∴∠BAE=∠ADF,
∴△ABE∽△DAG,
第 19页(共 39页)
∴ = ,
∴AB AG=AD BE,即 AB2= AD2,
∴AB=AD,
∴四边形 ABCD是正方形,
∴AB=BC=CD=AD=PQ,
设 AB=BC=CD=AD=PQ=4a,
则 BE=AG=2a,
∴tan∠ADG=tan∠BAE= = ,AE=DG= =2 a,
∵DF⊥AE,
∴AF= = = a,
∵PQ∥BC,
∴△APF∽△ABE,
∴ = = ,即 = = ,
解得:AP= a,PF= a,
∴CQ=PB=AB﹣AP=4a﹣ a= a,
FQ=PQ﹣PF=4a﹣ a= a,
∵KH⊥AD,
∴tan∠ADG= = ,
设 KH=x,则 DH=2x,
∵PQ∥AD,AK∥FC,
∴∠DAF=∠QFE,∠KAF=∠CFE,
∴∠DAK=∠QFC,
又∵∠AHK=∠FQC=90°,
∴△AHK∽△FQC,
∴ = ,即 = ,
第 20页(共 39页)
解得:AH= x,
∵AH+DH=AD,
∴ x+2x=4a,
解得:x= a,
∴KH= a,
∵△ADK的面积为 S1= AD×KH,△CDF的面积为 S2= CD×FQ,
∴ = = = ;
故答案为: .
5.【解答】解:(1)∵四边形 PEGF是平行四边形,
∴GF=PE,GF∥PE,
∴△DGF∽△DAE,
∴ ,
∵F是 DE的中点,
∴DF= DE,
∴ ,
第 21页(共 39页)
∴AE=2GF,
∴ ,
∴m= ,
故答案为: ;
(2)如图 1,
当点 G在矩形 ABCD的外部时,
作 GH⊥AD于 H,作射线 DG,交 PA的延长线于 W,作 WQ⊥PA,交 PA的延长线于点 Q,
由(1)得,
G是 DW的中点,
同理可得 WQ=2GH=2,PE=FG= WE,
设 PE=FG=x,则 WE=2x,
∵四边形 ABCD是矩形,
∴∠DAB=∠B=90°,
∵P时 BC的中点,
∴PB= BC=4,
∴AB=PB,
∴∠WAQ=∠DAP=∠PAB=45°,
∴AW= WQ=2 ,AP= AB=4 ,
∴WP=AW+AP=6 ,
由 WE+PE=WP得,
2x+x=6 ,
∴x=2 ,
第 22页(共 39页)
∴PE=2 ,
∴AE=AP﹣PE=2 ,
∴m=1,
如图 2,
当点 G在矩形 ABCD的内部时,
由上可知:AW=2 ,
∴PW=AP﹣﹣AW=2 ,
∴PE= PW= ,
∴AE=4 = ,
∴m= ,
综上所述:m=1或 ;
(3)如图 3,
当 m< 时,
延长 EP至 X,使 PX=EP,连接 DP,DX,
∵点 F是 DE的中点,
∴PF∥DX,
第 23页(共 39页)
∵EM∥PF,
∴EM∥DX,
∴∠AME=∠ADX,
∵GF∥PE,
∴∠MNG=∠DAX,
∴△MNG∽△DAX,
∴ ,
∵S△ADP= AD AB= , ,
∴S△DPX=S△DEP= S△ADP= ,
∴S△ADX=S△ADP+S△DPX=16+ = ,
设 AE=x,则 GF=PE=mx,
∵FN= AE= x,
∴NG=FN﹣GF= ,
∵AX=AE+PE+PX=x+2mx=(1+2m)x,
∴ =( )2,
∴S= ,
如图 4,
第 24页(共 39页)
当 m> 时,
同理可得,
,NG=FG﹣NF=(m﹣ )x,AX=(1+2m)x,
∴S= ,
综上所述:S= .
6.【解答】(1)解:∵△ABC是等边三角形,
∴AB=CA,∠BAE=∠C=60°,
在△ACD和△BAE中,
,
∴△ACD≌△BAE(SAS).
∴AD=BE,∠CAD=∠ABE,
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,
故答案为:AD=BE,60°;
(2)证明:由(1)可知,∠BFD=60°,
∴∠AFB=120°,
∵FG=BF,
∴△BFG是等边三角形,
∴BF=BG,∠FBG=∠BGF=60°,
第 25页(共 39页)
∵△ABC是等边三角形,
∴AB=CB,∠ABC=60°,
∴∠ABC=∠FBG,
∴∠ABC﹣∠FBD=∠FBG﹣∠FBD,
即∠ABF=∠CBG,
∴△ABF≌△CBG(SAS),
∴∠AFB=∠CGB=120°,
∴∠CGF=∠CGB﹣∠BGF=120°﹣60°=60°,
∴∠BGF=∠CGF,
∴GA平分∠BGC;
(3)解:如图 3,延长 FD至点 G,使 FG=BF,连接 BG、CG,过点 D作 DM⊥BG于点 M,DN⊥CG
于点 N,
∵AB=AC,FG=BF,
∴ = ,
∵∠BAC=∠BFD,
∴△ABC∽△FBG,
∴ = ,∠ABC=∠FBG,
∴∠ABC﹣∠CBE=∠FBG﹣∠CBE,
即∠ABF=∠CBG,
∴△ABF∽△CBG,
∴ = =3,∠BAF=∠BCG,
∵∠ADB=∠CDG,
∴∠CGD=∠ABD,
∵AB=AC,FG=BF,
第 26页(共 39页)
∴∠ABC=∠ACB,∠FBG=∠FGB,
∵∠BAC=∠BFD,
∴∠BAC=∠FGB,
∴∠CGD=∠FGB,
∴DG平分∠BGC,
∵DM⊥BG,DN⊥CG,
∴DM=DN,
∵S△BGD= BG DM,S△CGD= CG DN,
∴ = = =3,
又∵ = ,
∴ =3.
方法二:如图 4,过点 D作 DP∥AB交 AC于点 P,
则∠BAF=∠ADP,∠ABC=∠PDC,
∵∠BAC=∠BFD,∠BFD=∠ABF+∠BAF,∠BAC=∠BAF+∠DAP,
∴∠ABF=∠DAP,
∴△ABF∽△DAP,
∴ = ,
即 = =3,
∵AB=AC,
∴∠ABC=∠ACB=∠PDC,
∴PD=PC,
第 27页(共 39页)
∵DP∥AB,
∴ = = =3.
7.【解答】解:(1)①由图②知,△ECD的面积为 6,
∴ CD AD=6,
∴CD AD=12,
∴矩形 ABCD的面积为 12;
故答案为:12;
②由图②知,正方形 DEFG的面积最大为 25,此时边 DE最大,E与 B重合,
∴AB2+AD2=25,
由矩形 ABCD,结合①可知 AB AD=CD AD=12,
∴AB+AD= = =7,
∴矩形 ABCD的周长为 14;
(2)E、C、G三点不能共线,理由如下:
由(1)知 AB+AD=7,AB AD=12,
∴AB=3,AD=4(AB为矩形 ABCD的较短边,AB=4,AD=3已舍去),
以 A为原点,AD所在直线为 x轴建立直角坐标系,过 G作 GK⊥CD交 DC延长线于 K,如图:
∵∠KDG=90°﹣∠EDC=∠EDA,∠K=90°=∠EAD,DE=DG,
∴△DKG≌△DAE(AAS),
∴DK=AD=4,KG=AE,
设 AE=m,则 KG=m,
∴E(0,m),G(4+m,4),
第 28页(共 39页)
∴直线 EG函数表达式为 y= x+m,
若 C(4,3)在直线 EG上,则 3= ×4+m,
变形整理得:m2﹣3m+4=0,
∵Δ=(﹣3)2﹣4×4=﹣7<0,
∴C(4,3)不可能满足 y= x+m,
∴C不可能在直线 EG上,故 E、C、G三点不能共线;
(3)过 F作 FT⊥y轴于 T,FW⊥BC于 W,如图:
∵∠TEF=90°﹣∠AED=∠ADE,∠ETF=90°=∠EAD,EF=ED,
∴△EFT≌△DEA(AAS),
∴TF=AE,TE=AD=4,
∵BE=x,
∴AE=AB﹣BE=3﹣x=TF,
∵BH∥TF,
∴ = 即 = ,
∴BH=﹣ + x,
∴CH=4﹣BH= ﹣ x+4,
∴S1= BE TF= x (3﹣x)=﹣ x2+ x,S2= CH TE= ( ﹣ x+4)×4= ﹣ x+8,
∴ = =﹣1+ ,
第 29页(共 39页)
当 x2﹣3x+16最小时, 最大,从而 最大,
∵x2﹣3x+16=(x﹣ )2+ ,
∴当 x= 时,x2﹣3x+16最小为 ,此时 取得最大值,
∴BE= ,
∴AE=TF=3﹣ = ,TB=TE﹣BE=4﹣ = ,
∴BW=TF= ,FW=TB= ,
∴CW=BC﹣BW=4﹣ = ,
∴CW=FW,
∴△CFW是等腰直角三角形,
∴∠FCB=45°,
∵∠EGD=45°,
∴∠FCB=∠EGD,
由(2)知 C不在 EG上,
∴∠CGD≠∠FCB.
∴当 x= 时, 取得最大值,此时∠FCB与∠CGD不相等.
8.【解答】解:(1)如图 1,过 D作 DM⊥BC于 M,则四边形 ABMD是矩形,
∴AB=DM,BM=AD=3(矩形性质),
∴CM=BC﹣BM=2,
在 Rt△CDM中,
由勾股定理得 ,
第 30页(共 39页)
∴AB=4,
∴AB的长为 4;
(2)不存在,理由如下:
如图 2,过 P作 PH∥AD交 BD于 G,交 CD于 H,
∴PH∥AD∥BC,
∴∠ADP=∠DPG,∠HPC=∠BCP(两直线平行,内错角相等),
∠GHD=∠BCD(两直线平行,同位角相等),
∵PC平分∠BCD,
∴∠ADP=∠PDG(角平分线的性质),
∴∠DPG=∠PDG,
∴PG=DG(等角对等边),
在 Rt△ABD中, ,
由勾股定理得 ,
∴BD=BC,
∴∠BDC=∠BCD,
∴∠GHD=∠BDC,
∴DG=GH,
∴PG=DG=GH,
设 PG=DG=GH=a,则 BG=5﹣a, ,
∵∠PBG=∠ABD,∠BPG=∠A=90°,
∴△PBG∽△ABD,
∴ ,
即 ,
第 31页(共 39页)
解得 ,
∴ ,
∵GH∥BC,
∴△DGH∽△DBC,
∴ ,即 ,
解得 ,
∴ ,
若 PD平分∠ADB,则∠BCP=∠HCP=∠HPC,即 PH=CH,
∵ ,与 PH=CH矛盾,
∴不存在这样的点 P,使得 PC平分∠BCD、PD平分∠ADB同时成立;
(3)令△PEF中 PE边上的高为 h1,△PCD中 PC边上的高为 h2,
∵PF∥CD,
∴∠PFE=∠CDE,∠FPE=∠DCE,
∴△PFE∽△CDE,
设 ,则 ,
∴PE=kCE,h1=kh2,
∴ ,
,
∵S2=6S1,即 ,
整理得 6k2﹣k﹣1=0,则(2k﹣1)(3k+1)=0,
解得 , (舍去),
∴ ,
如图 3,过 E作 EQ∥AD交 AB于 Q,
第 32页(共 39页)
∴QE∥BC,
∴△PQE∽△PBC,
∴ ,
即 ,
∴ , ,
∵QE∥AD,
∴△BEQ∽△BDA,
∴ ,即 ,
解得 ,
∴ ,
∴ ,
∴AP的长为 .
9.【解答】解:(1)如图 1,△BCD≌△ACE,理由如下:
∵△ABC与△CDE都是等边三角形,
∴BC=AC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE(SAS);
(2)如图 2,过点 D作 DG⊥BC于 D点 G,
第 33页(共 39页)
∵△ABC是边长为 3的等边三角形,AD=2BD,
∴∠ABC=∠ACB=60°,BD=1,AD=2,
∵DG⊥BC,
∴BG= ,
DG= BG= ,
由(1)得,△BCD≌△ACE,
∴AE=BD=1,∠CAE=∠CBA=60°,
∴∠CAE=∠ACB,
∴AE∥CH,
∴△ADE∽△BDH,
∴ ,
∵AD=2BD,AE=1,
∴ ,
∴BH= ,
∴GH=BH+BG=1,
∵DG⊥BC,
∴tan∠DHC= ;
(3)如图 3,过点 C作 CH⊥AB于点 H,
∵△ABC与△CDE都是等边三角形,
∴BC=AC,DC=EC,
第 34页(共 39页)
∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE(SAS),
∴∠BDC=∠AEC,
又∵∠AFD=∠CFE,
∴△AFD∽△CFE,
∴ ,
∵S2=4S1,
∴CE=2AD,
设 BD=x,
则 AD=BD﹣AB=x﹣3,
CD=CE=2(x﹣3)=2x﹣6,
∵CH⊥AB,△ABC是边长为 3的等边三角形,
∴AH= ,
CH= AH= ,
∴DH=AH+AD= ,
∵CH⊥AB,
∴CH2+DH2=CD2,
即( ) =(2x﹣6)2,
解得 x= ,
∵点 D在 BA的延长线上,
∴BD>AB,
∴x>3,
第 35页(共 39页)
∴x= ,
即 BD= .
10.【解答】(1)证明:连接 OD,
∴OD=OB
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为 BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵BC是以 AB为直径的⊙O的切线,
∴AB⊥BC,
∴∠EBO=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)∵S2=5 S1
∴S△ADB=2S△CDB
∴
∵△BDC∽△ADB
∴
∴DB2=AD DC
第 36页(共 39页)
∴ =
∴tan∠BAC= = .
(3)∵tan∠BAC= =
∴ = ,得 BC= AB
∵E为 BC的中点
∴BE= AB
∵AE=3 ,
∴在 Rt△AEB中,由勾股定理得
,解得 AB=4
故⊙O的半径 R= AB=2.
11.【解答】解:(1)∵DF∥BC,EF∥AB,
∴∠AFD=∠ACB,∠DAF=∠EFC,
∴△ADF∽△FEC,
∵△ADF、△EFC的面积分别为 3,1,
∴ ,
∴ ,
∵△ADF的边 DF上的高为 h1,△EFC的边 CE上的高为 h2,
∴ ;
故答案为: .
(2)证明:如图①,设 AD=a,BD=b,DB与 EF间的距离为 h,
第 37页(共 39页)
∵EF∥AB,DF∥BC,
∴四边形 DBFE是平行四边形,
∴BD=EF=b,
由(1)知△ADF∽△FEC,
∴ ,
∵S1= ah,
∴S2= ,
∴S1S2= ,
∴bh=2 ,
∵S=bh,
∴S=2 .
(3)如图②,过点 D作 DM∥AC交 BC于点 M,
∴∠DMF=∠ECG,
∵DE∥BC,DF∥EG,
第 38页(共 39页)
∴四边形 DFGE为平行四边形,
∴DF=EG,∠DFM=∠EGC,
∴△DFM≌△EGC(AAS),
∴S△DFM=S△EGC=5,
∵S△DBF=7,
∴S△BDM=7+5=12,
∵DE∥BM,DM∥AC,
∴∠ADE=∠DBM,∠BDM=∠BAE,
∴△DAE∽△BDM,
∴ = ,
∴ ,
∴ ,
同理,△ADE∽△ABC,
∴S△ABC=9S△ADE=9×3=27.
第 39页(共 39页)
同课章节目录
