19.2.2.3 用待定系数法求一次函数的解析式同步练习(含答案)
文档属性
| 名称 | 19.2.2.3 用待定系数法求一次函数的解析式同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 20:36:14 | ||
图片预览




文档简介
19.2 一次函数
19.2.2 正比例函数
第3课时 用待定系数法求一次函数的解析式
一、选择题
1.函数y=kx的图象经过点P(-1,3),则k的值为( )
A.3 B.-3 C. D.-
2.直线y=kx-4经过点(-2,2),则该直线的解析式是( )
A.y=-3x-4 B.y=-x-4 C.y=x-4 D.y=3x-4
3.已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( )
A.y=x-2 B.y=x+2 C.y=-x-2 D.y=-x+2
4.如图,在直角坐标系中,直线l所表示的一次函数是( )
A.y=3x+3 B.y=3x-3 C.y=-3x+3 D.y=-3x-3
第4题图 第5题图 第6题图
5.如图,已知直线l1:y=-2x+4与坐标轴分别交于A,B两点,那么过原点O且将△AOB的面积平分的直线l2的解析式为( )
A.y=x B.y=x C.y=x D.y=2x
6.象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( )
A.y=x+1 B.y=x-1 C.y=2x+1 D.y=2x-1
7.已知在一次函数y=kx+b中,当x=1时,y=1;当x=2时,y=-4.则一次函数的解析式为( )
A.y=-5x+6 B.y=-3x+4 C.y=3x-2 D.y=6x-5
8.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴,y轴分别交于点A,B,则△AOB的面积为( )
A. B. C.4 D.8
9.已知一次函数y=kx+b(k≠0),当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( )
A.12 B.-6 C.-6或-12 D.6或12
10.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为( )
A.y=-x+4 B.y=-x+4 C.y=-x+4 D.y=4
二、填空题
11.函数y=kx+3的图象经过点(2,5),则k= .
12.一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式: .
13.在一次函数y=kx+b中,当x=1时,y=-1;当x=2时,y=3,则当x=-2时,y的值是 .
14.如图,一次函数y=x+6的图象与x轴、y轴分别交于点A,B,过点B的直线平分△ABO的面积,则直线BC相应的函数解析式为 .
第14题图 第16题图 第17题图
15.已知一次函数y=kx+b(k≠0)的图象经过点A(3,0),与y轴交于点B,O为坐标原点.若△AOB的面积为6,则该一次函数的解析式为 .
16.如图,已知A(2,3),B(0,2),在x轴上找一点C,使得|AC-BC|的值最大,则此时点C的坐标为 .
17.如图,在平面直角坐标系中,已知点A(2,4),B(1,2),C(5,2),直线l经过点A,它将△ABC分成面积相等的两部分,则直线l的解析式为 .
18.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了平面直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数解析式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于 .
三、解答题
19.(1)已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点,求解析式;
(2)已知直线y=kx+b与y=-2x+3平行,且与y轴的交点为P(0,5),求k,b的值.
20.在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A,B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A,C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
21.如图,在平面直角坐标系中,点A(2,m)在直线y=2x-上,过点A的直线交y轴于点B(0,3).
(1)求m的值和直线AB的函数解析式;
(2)若点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,求y1-y2的最大值.
22.一次函数y=kx+b的图象经过A(1,6),B(-3,-2)两点.
(1)求此一次函数的解析式;
(2)求△AOB的面积.
23.如图,过点A(3,0)的两条直线l1,l2,分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=5.
(1)求点B的坐标;
(2)若△ABC的面积为9,求直线l2的函数解析式.
24.已知一次函数y=kx+b的图象过P(1,4),Q(4,1)两点,且与x轴交于A点.
(1)求此一次函数的解析式;
(2)求△POQ的面积;
(3)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值.
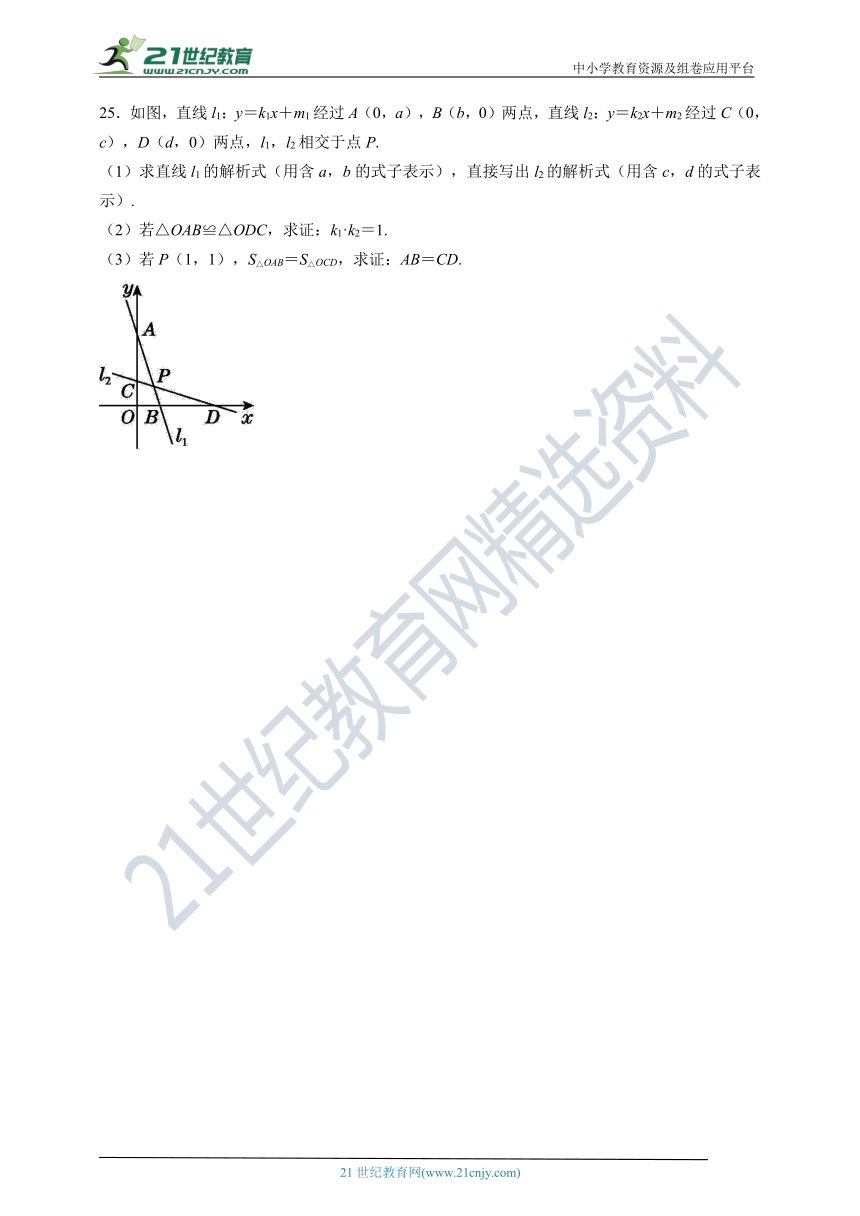
25.如图,直线l1:y=k1x+m1经过A(0,a),B(b,0)两点,直线l2:y=k2x+m2经过C(0,c),D(d,0)两点,l1,l2相交于点P.
(1)求直线l1的解析式(用含a,b的式子表示),直接写出l2的解析式(用含c,d的式子表示).
(2)若△OAB≌△ODC,求证:k1·k2=1.
(3)若P(1,1),S△OAB=S△OCD,求证:AB=CD.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.函数y=kx的图象经过点P(-1,3),则k的值为( B )
A.3 B.-3 C. D.-
2.直线y=kx-4经过点(-2,2),则该直线的解析式是( A )
A.y=-3x-4 B.y=-x-4 C.y=x-4 D.y=3x-4
3.已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( A )
A.y=x-2 B.y=x+2 C.y=-x-2 D.y=-x+2
4.如图,在直角坐标系中,直线l所表示的一次函数是( A )
A.y=3x+3 B.y=3x-3 C.y=-3x+3 D.y=-3x-3
第4题图 第5题图 第6题图
5.如图,已知直线l1:y=-2x+4与坐标轴分别交于A,B两点,那么过原点O且将△AOB的面积平分的直线l2的解析式为( D )
A.y=x B.y=x C.y=x D.y=2x
6.象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( A )
A.y=x+1 B.y=x-1 C.y=2x+1 D.y=2x-1
7.已知在一次函数y=kx+b中,当x=1时,y=1;当x=2时,y=-4.则一次函数的解析式为( A )
A.y=-5x+6 B.y=-3x+4 C.y=3x-2 D.y=6x-5
8.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴,y轴分别交于点A,B,则△AOB的面积为( B )
A. B. C.4 D.8
9.已知一次函数y=kx+b(k≠0),当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( C )
A.12 B.-6 C.-6或-12 D.6或12
10.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为( A )
A.y=-x+4 B.y=-x+4 C.y=-x+4 D.y=4
【解析】过点D作DH⊥x轴于点H,如图,由题意及正方形的性质易证△ABO≌△DAH,∴AH=4,DH=3,∴D(7,3),由B,D的坐标可得直线BD的解析式为y=-x+4.
二、填空题
11.函数y=kx+3的图象经过点(2,5),则k= .
【答案】1
12.一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式: .
【答案】y=x+2(答案不唯一)
13.在一次函数y=kx+b中,当x=1时,y=-1;当x=2时,y=3,则当x=-2时,y的值是 .
【答案】-13
14.如图,一次函数y=x+6的图象与x轴、y轴分别交于点A,B,过点B的直线平分△ABO的面积,则直线BC相应的函数解析式为 .
【答案】y=x+6
第14题图 第16题图 第17题图
15.已知一次函数y=kx+b(k≠0)的图象经过点A(3,0),与y轴交于点B,O为坐标原点.若△AOB的面积为6,则该一次函数的解析式为 .
【答案】y=x-4或y=-x+4
16.如图,已知A(2,3),B(0,2),在x轴上找一点C,使得|AC-BC|的值最大,则此时点C的坐标为 .
【答案】(-4,0)
17.如图,在平面直角坐标系中,已知点A(2,4),B(1,2),C(5,2),直线l经过点A,它将△ABC分成面积相等的两部分,则直线l的解析式为 .
【答案】y=-2x+8
【解析】当直线l经过点A和BC边的中点时,将△ABC分成面积相等的两部分,∵B(1,2),C(5,2),∴BC边中点的坐标为,即(3,2).
设直线l的解析式为y=kx+b,把点A(2,4),BC边中点的坐标代入得
解得
∴直线l的解析式为y=-2x+8.
18.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了平面直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数解析式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于 .
【答案】5
【解析】设y1=k1x+b1的图象过A(0,2),B(2,3),则有
解得则k1+b1=+2=;
设y2=k2x+b2的图象过B(2,3),C(3,1),y3=k3x+b3的图象过A(0,2),C(3,1),同理,k2+b2=-2+7=5,k3+b3=-+2=.
则其中最大的值为5.
三、解答题
19.(1)已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点,求解析式;
(2)已知直线y=kx+b与y=-2x+3平行,且与y轴的交点为P(0,5),求k,b的值.
解:(1)y=x+2.
(2)k=-2,b=5.
20.在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A,B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A,C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
解:(1)∵点A与点B关于y轴对称,
∴a+2+2a-5=0,解得a=1.
∴A点坐标为(3,0),B点坐标为(-3,0).
∵矩形ABCD的边BC=3,
∴C点坐标为(-3,-3).
解:(2)设直线AC的解析式为
y=mx+n,
把A(3,0),C(-3,-3)代入,
解得m=,n=-.
∴直线AC的解析式为y=x-.
由题意知,k=,且y=kx+b过点B(-3,0),
∴×(-3)+b=0,b=.∴经过点B且与AC平行的直线的解析式为y=x+.
21.如图,在平面直角坐标系中,点A(2,m)在直线y=2x-上,过点A的直线交y轴于点B(0,3).
(1)求m的值和直线AB的函数解析式;
(2)若点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,求y1-y2的最大值.
解:(1)把点A(2,m)代入y=2x-中,得m=.
设直线AB的函数解析式为y=kx+b,把A,B(0,3)代入, 解得
k=-,b=3.
∴直线AB的函数解析式为y=-x+3.
解:(2)∵点P(t,y1)在线段AB上,
∴y1=-t+3(0≤t≤2).
同理,y2=2(t-1)-=2t-.
∴y1-y2=-t+3-=-t+.
∵-<0,∴y1-y2随t的增大而减小,
∴当t=0时,y1-y2取得最大值,最大值为.
22.一次函数y=kx+b的图象经过A(1,6),B(-3,-2)两点.
(1)求此一次函数的解析式;
(2)求△AOB的面积.
解:(1)把A(1,6),B(-3,-2)代入y=kx+b,得
解得
所以一次函数解析式为y=2x+4.
(2)直线AB与y轴的交点坐标为(0,4),
所以△AOB的面积为×4×3+×4×1=8.
23.如图,过点A(3,0)的两条直线l1,l2,分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=5.
(1)求点B的坐标;
(2)若△ABC的面积为9,求直线l2的函数解析式.
解:(1)B(0,4).
(2)∵S△ABC=·BC·OA=×BC×3=9,
∴BC=6,∵OB=4,∴OC=2,∴C(0,-2).
设l2的解析式为y=kx+b,将A(3,0)和C(0,-2)代入,得k=,b=-2,
∴直线l2的解析式为y=x-2.
24.已知一次函数y=kx+b的图象过P(1,4),Q(4,1)两点,且与x轴交于A点.
(1)求此一次函数的解析式;
(2)求△POQ的面积;
(3)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值.
解:(1)把P(1,4),Q(4,1)代入一次函数解析式,得解得
则此一次函数的解析式为y=-x+5.
(2)对于一次函数y=-x+5.
令y=0,得到x=5,∴A(5,0),
∴S△POQ=S△POA-S△AOQ=×5×4-×5×1=7.5.
(3)如图,作Q点关于x轴的对称点Q′,连接PQ′交x轴于点M,则MP+MQ的值最小.
∵Q(4,1),∴Q′(4,-1).
设直线PQ′的解析式为y=mx+n.
则解得
∴直线PQ′的解析式为y=-x+.
当y=0时,-x+=0,解得x=,
∴点M的坐标为(,0),
MP+MQ的最小值为=.
25.如图,直线l1:y=k1x+m1经过A(0,a),B(b,0)两点,直线l2:y=k2x+m2经过C(0,c),D(d,0)两点,l1,l2相交于点P.
(1)求直线l1的解析式(用含a,b的式子表示),直接写出l2的解析式(用含c,d的式子表示).
(2)若△OAB≌△ODC,求证:k1·k2=1.
(3)若P(1,1),S△OAB=S△OCD,求证:AB=CD.
(1)解:∵直线l1:y=k1x+m1经过A(0,a),B(b,0)两点,
∴解得
∴l1:y=-x+a.l2:y=-x+c.
(2)证明:∵△OAB≌△ODC,∴a=d,b=c.由(1)知k1=-,k2=-,∴k1·k2=-·=·=1.
(3)证明:将点P(1,1)代入l1,l2的解析式中可得1=-+a,1=-+c.∴ab=a+b,cd=c+d.
∴(ab)2=(a+b)2=a2+b2+2ab.∴(2S△OAB)2=AB2+4S△OAB,同理可得(2S△OCD)2=CD2+4S△OCD.
∵S△OAB=S△OCD,
∴AB=CD.
19.2.2 正比例函数
第3课时 用待定系数法求一次函数的解析式
一、选择题
1.函数y=kx的图象经过点P(-1,3),则k的值为( )
A.3 B.-3 C. D.-
2.直线y=kx-4经过点(-2,2),则该直线的解析式是( )
A.y=-3x-4 B.y=-x-4 C.y=x-4 D.y=3x-4
3.已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( )
A.y=x-2 B.y=x+2 C.y=-x-2 D.y=-x+2
4.如图,在直角坐标系中,直线l所表示的一次函数是( )
A.y=3x+3 B.y=3x-3 C.y=-3x+3 D.y=-3x-3
第4题图 第5题图 第6题图
5.如图,已知直线l1:y=-2x+4与坐标轴分别交于A,B两点,那么过原点O且将△AOB的面积平分的直线l2的解析式为( )
A.y=x B.y=x C.y=x D.y=2x
6.象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( )
A.y=x+1 B.y=x-1 C.y=2x+1 D.y=2x-1
7.已知在一次函数y=kx+b中,当x=1时,y=1;当x=2时,y=-4.则一次函数的解析式为( )
A.y=-5x+6 B.y=-3x+4 C.y=3x-2 D.y=6x-5
8.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴,y轴分别交于点A,B,则△AOB的面积为( )
A. B. C.4 D.8
9.已知一次函数y=kx+b(k≠0),当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( )
A.12 B.-6 C.-6或-12 D.6或12
10.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为( )
A.y=-x+4 B.y=-x+4 C.y=-x+4 D.y=4
二、填空题
11.函数y=kx+3的图象经过点(2,5),则k= .
12.一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式: .
13.在一次函数y=kx+b中,当x=1时,y=-1;当x=2时,y=3,则当x=-2时,y的值是 .
14.如图,一次函数y=x+6的图象与x轴、y轴分别交于点A,B,过点B的直线平分△ABO的面积,则直线BC相应的函数解析式为 .
第14题图 第16题图 第17题图
15.已知一次函数y=kx+b(k≠0)的图象经过点A(3,0),与y轴交于点B,O为坐标原点.若△AOB的面积为6,则该一次函数的解析式为 .
16.如图,已知A(2,3),B(0,2),在x轴上找一点C,使得|AC-BC|的值最大,则此时点C的坐标为 .
17.如图,在平面直角坐标系中,已知点A(2,4),B(1,2),C(5,2),直线l经过点A,它将△ABC分成面积相等的两部分,则直线l的解析式为 .
18.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了平面直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数解析式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于 .
三、解答题
19.(1)已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点,求解析式;
(2)已知直线y=kx+b与y=-2x+3平行,且与y轴的交点为P(0,5),求k,b的值.
20.在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A,B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A,C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
21.如图,在平面直角坐标系中,点A(2,m)在直线y=2x-上,过点A的直线交y轴于点B(0,3).
(1)求m的值和直线AB的函数解析式;
(2)若点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,求y1-y2的最大值.
22.一次函数y=kx+b的图象经过A(1,6),B(-3,-2)两点.
(1)求此一次函数的解析式;
(2)求△AOB的面积.
23.如图,过点A(3,0)的两条直线l1,l2,分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=5.
(1)求点B的坐标;
(2)若△ABC的面积为9,求直线l2的函数解析式.
24.已知一次函数y=kx+b的图象过P(1,4),Q(4,1)两点,且与x轴交于A点.
(1)求此一次函数的解析式;
(2)求△POQ的面积;
(3)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值.
25.如图,直线l1:y=k1x+m1经过A(0,a),B(b,0)两点,直线l2:y=k2x+m2经过C(0,c),D(d,0)两点,l1,l2相交于点P.
(1)求直线l1的解析式(用含a,b的式子表示),直接写出l2的解析式(用含c,d的式子表示).
(2)若△OAB≌△ODC,求证:k1·k2=1.
(3)若P(1,1),S△OAB=S△OCD,求证:AB=CD.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.函数y=kx的图象经过点P(-1,3),则k的值为( B )
A.3 B.-3 C. D.-
2.直线y=kx-4经过点(-2,2),则该直线的解析式是( A )
A.y=-3x-4 B.y=-x-4 C.y=x-4 D.y=3x-4
3.已知一次函数的图象过点(2,0)和点(1,-1),则这个函数的解析式为( A )
A.y=x-2 B.y=x+2 C.y=-x-2 D.y=-x+2
4.如图,在直角坐标系中,直线l所表示的一次函数是( A )
A.y=3x+3 B.y=3x-3 C.y=-3x+3 D.y=-3x-3
第4题图 第5题图 第6题图
5.如图,已知直线l1:y=-2x+4与坐标轴分别交于A,B两点,那么过原点O且将△AOB的面积平分的直线l2的解析式为( D )
A.y=x B.y=x C.y=x D.y=2x
6.象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数解析式为( A )
A.y=x+1 B.y=x-1 C.y=2x+1 D.y=2x-1
7.已知在一次函数y=kx+b中,当x=1时,y=1;当x=2时,y=-4.则一次函数的解析式为( A )
A.y=-5x+6 B.y=-3x+4 C.y=3x-2 D.y=6x-5
8.一次函数y=-2x+m的图象经过点P(-2,3),且与x轴,y轴分别交于点A,B,则△AOB的面积为( B )
A. B. C.4 D.8
9.已知一次函数y=kx+b(k≠0),当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( C )
A.12 B.-6 C.-6或-12 D.6或12
10.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为( A )
A.y=-x+4 B.y=-x+4 C.y=-x+4 D.y=4
【解析】过点D作DH⊥x轴于点H,如图,由题意及正方形的性质易证△ABO≌△DAH,∴AH=4,DH=3,∴D(7,3),由B,D的坐标可得直线BD的解析式为y=-x+4.
二、填空题
11.函数y=kx+3的图象经过点(2,5),则k= .
【答案】1
12.一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式: .
【答案】y=x+2(答案不唯一)
13.在一次函数y=kx+b中,当x=1时,y=-1;当x=2时,y=3,则当x=-2时,y的值是 .
【答案】-13
14.如图,一次函数y=x+6的图象与x轴、y轴分别交于点A,B,过点B的直线平分△ABO的面积,则直线BC相应的函数解析式为 .
【答案】y=x+6
第14题图 第16题图 第17题图
15.已知一次函数y=kx+b(k≠0)的图象经过点A(3,0),与y轴交于点B,O为坐标原点.若△AOB的面积为6,则该一次函数的解析式为 .
【答案】y=x-4或y=-x+4
16.如图,已知A(2,3),B(0,2),在x轴上找一点C,使得|AC-BC|的值最大,则此时点C的坐标为 .
【答案】(-4,0)
17.如图,在平面直角坐标系中,已知点A(2,4),B(1,2),C(5,2),直线l经过点A,它将△ABC分成面积相等的两部分,则直线l的解析式为 .
【答案】y=-2x+8
【解析】当直线l经过点A和BC边的中点时,将△ABC分成面积相等的两部分,∵B(1,2),C(5,2),∴BC边中点的坐标为,即(3,2).
设直线l的解析式为y=kx+b,把点A(2,4),BC边中点的坐标代入得
解得
∴直线l的解析式为y=-2x+8.
18.在“探索一次函数y=kx+b的系数k,b与图象的关系”活动中,老师给出了平面直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数解析式y1=k1x+b1,y2=k2x+b2,y3=k3x+b3.分别计算k1+b1,k2+b2,k3+b3的值,其中最大的值等于 .
【答案】5
【解析】设y1=k1x+b1的图象过A(0,2),B(2,3),则有
解得则k1+b1=+2=;
设y2=k2x+b2的图象过B(2,3),C(3,1),y3=k3x+b3的图象过A(0,2),C(3,1),同理,k2+b2=-2+7=5,k3+b3=-+2=.
则其中最大的值为5.
三、解答题
19.(1)已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点,求解析式;
(2)已知直线y=kx+b与y=-2x+3平行,且与y轴的交点为P(0,5),求k,b的值.
解:(1)y=x+2.
(2)k=-2,b=5.
20.在平面直角坐标系中,矩形ABCD的边AB在x轴上,点A,B的横坐标分别为a+2与2a-5,且关于y轴对称,BC的长为3,且点C在第三象限.
(1)求顶点A,C的坐标;
(2)若y=kx+b是经过点B,且与AC平行的一条直线,试确定它的解析式.
解:(1)∵点A与点B关于y轴对称,
∴a+2+2a-5=0,解得a=1.
∴A点坐标为(3,0),B点坐标为(-3,0).
∵矩形ABCD的边BC=3,
∴C点坐标为(-3,-3).
解:(2)设直线AC的解析式为
y=mx+n,
把A(3,0),C(-3,-3)代入,
解得m=,n=-.
∴直线AC的解析式为y=x-.
由题意知,k=,且y=kx+b过点B(-3,0),
∴×(-3)+b=0,b=.∴经过点B且与AC平行的直线的解析式为y=x+.
21.如图,在平面直角坐标系中,点A(2,m)在直线y=2x-上,过点A的直线交y轴于点B(0,3).
(1)求m的值和直线AB的函数解析式;
(2)若点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,求y1-y2的最大值.
解:(1)把点A(2,m)代入y=2x-中,得m=.
设直线AB的函数解析式为y=kx+b,把A,B(0,3)代入, 解得
k=-,b=3.
∴直线AB的函数解析式为y=-x+3.
解:(2)∵点P(t,y1)在线段AB上,
∴y1=-t+3(0≤t≤2).
同理,y2=2(t-1)-=2t-.
∴y1-y2=-t+3-=-t+.
∵-<0,∴y1-y2随t的增大而减小,
∴当t=0时,y1-y2取得最大值,最大值为.
22.一次函数y=kx+b的图象经过A(1,6),B(-3,-2)两点.
(1)求此一次函数的解析式;
(2)求△AOB的面积.
解:(1)把A(1,6),B(-3,-2)代入y=kx+b,得
解得
所以一次函数解析式为y=2x+4.
(2)直线AB与y轴的交点坐标为(0,4),
所以△AOB的面积为×4×3+×4×1=8.
23.如图,过点A(3,0)的两条直线l1,l2,分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=5.
(1)求点B的坐标;
(2)若△ABC的面积为9,求直线l2的函数解析式.
解:(1)B(0,4).
(2)∵S△ABC=·BC·OA=×BC×3=9,
∴BC=6,∵OB=4,∴OC=2,∴C(0,-2).
设l2的解析式为y=kx+b,将A(3,0)和C(0,-2)代入,得k=,b=-2,
∴直线l2的解析式为y=x-2.
24.已知一次函数y=kx+b的图象过P(1,4),Q(4,1)两点,且与x轴交于A点.
(1)求此一次函数的解析式;
(2)求△POQ的面积;
(3)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值.
解:(1)把P(1,4),Q(4,1)代入一次函数解析式,得解得
则此一次函数的解析式为y=-x+5.
(2)对于一次函数y=-x+5.
令y=0,得到x=5,∴A(5,0),
∴S△POQ=S△POA-S△AOQ=×5×4-×5×1=7.5.
(3)如图,作Q点关于x轴的对称点Q′,连接PQ′交x轴于点M,则MP+MQ的值最小.
∵Q(4,1),∴Q′(4,-1).
设直线PQ′的解析式为y=mx+n.
则解得
∴直线PQ′的解析式为y=-x+.
当y=0时,-x+=0,解得x=,
∴点M的坐标为(,0),
MP+MQ的最小值为=.
25.如图,直线l1:y=k1x+m1经过A(0,a),B(b,0)两点,直线l2:y=k2x+m2经过C(0,c),D(d,0)两点,l1,l2相交于点P.
(1)求直线l1的解析式(用含a,b的式子表示),直接写出l2的解析式(用含c,d的式子表示).
(2)若△OAB≌△ODC,求证:k1·k2=1.
(3)若P(1,1),S△OAB=S△OCD,求证:AB=CD.
(1)解:∵直线l1:y=k1x+m1经过A(0,a),B(b,0)两点,
∴解得
∴l1:y=-x+a.l2:y=-x+c.
(2)证明:∵△OAB≌△ODC,∴a=d,b=c.由(1)知k1=-,k2=-,∴k1·k2=-·=·=1.
(3)证明:将点P(1,1)代入l1,l2的解析式中可得1=-+a,1=-+c.∴ab=a+b,cd=c+d.
∴(ab)2=(a+b)2=a2+b2+2ab.∴(2S△OAB)2=AB2+4S△OAB,同理可得(2S△OCD)2=CD2+4S△OCD.
∵S△OAB=S△OCD,
∴AB=CD.
