数学人教A版(2019)必修第二册7.1复数的概念 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册7.1复数的概念 课件(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 01:35:54 | ||
图片预览





文档简介
(共24张PPT)
第七章 复数
7.1 复数的概念
7.1.1 数系的扩充和复数的概念
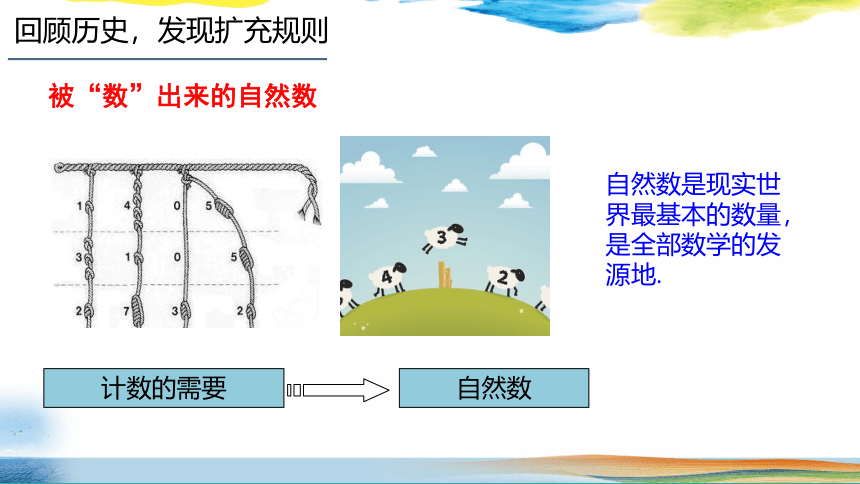
计数的需要
自然数
被“数”出来的自然数
自然数是现实世界最基本的数量,是全部数学的发源地.
回顾历史,发现扩充规则
相反量的需要
负数
被“欠”出来的负数
负数的引入,解决了在数集中不够减的矛盾.
吐鲁番盆地大约比海平面低155米.
+8844
-155
珠穆朗玛峰大约比海平面高8844米.
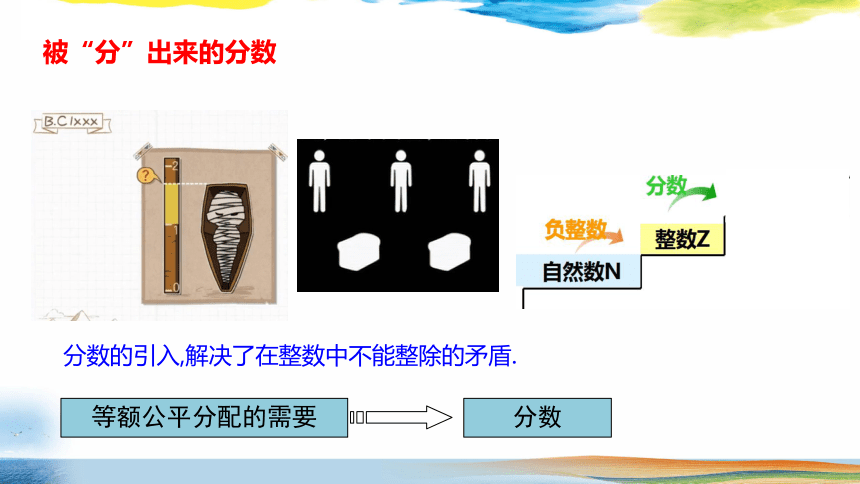
等额公平分配的需要
分数
被“分”出来的分数
分数的引入,解决了在整数中不能整除的矛盾.
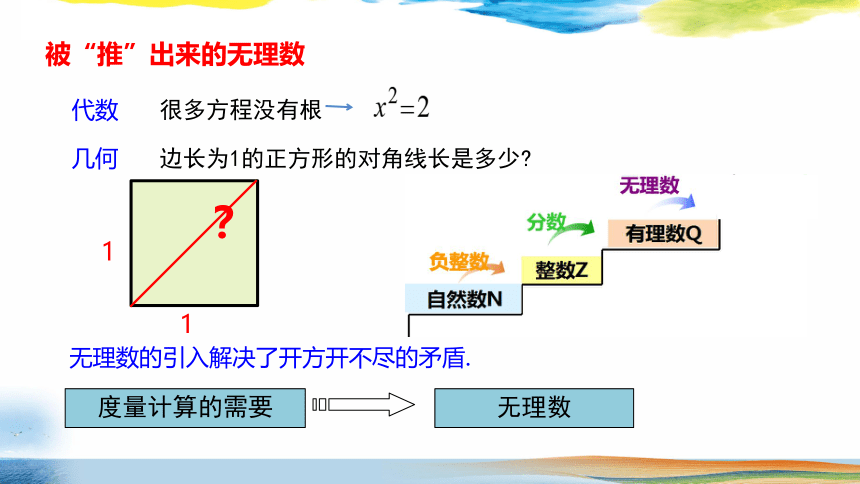
度量计算的需要
无理数
1
1
边长为1的正方形的对角线长是多少
被“推”出来的无理数
无理数的引入解决了开方开不尽的矛盾.
?
很多方程没有根
代数
几何
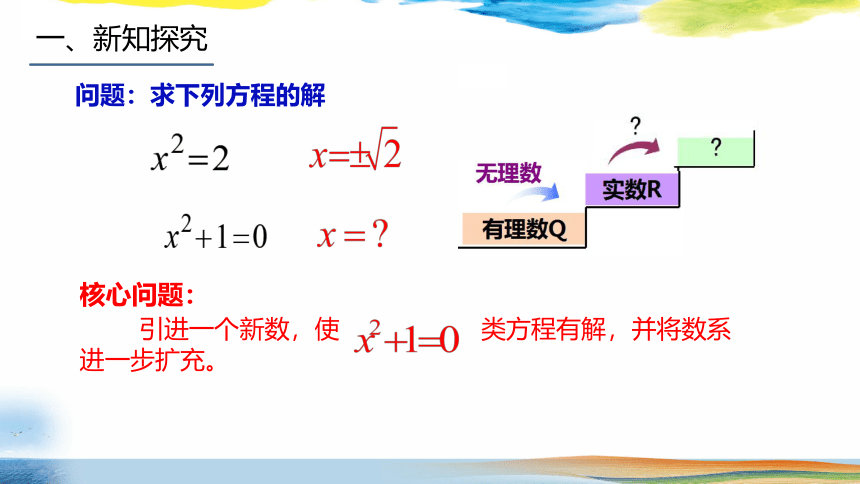
问题:求下列方程的解
核心问题:
引进一个新数,使 类方程有解,并将数系
进一步扩充。
一、新知探究
引入一个新数
1777年,欧拉首次提出用i表示平方等于-1的新数
1801年,高斯系统使用了i这个符号,使之通行于世
新数集
问题:用数i,1,2,这三个数中的若干个进行加法乘法运算,能写出哪些式子?
(1)形如 的数叫做复数,通常用字母 z 表示.
(2)全体复数所形成的集合叫做复数集,一般用C 表示.
实部
虚部
1 、复数的概念
虚数单位,i2=-1
思考:复数集与实数集具有什么关系呢?
2 、复数的分类
实数R
纯虚数
虚数
复数集C
3 、复数相等
规定:
复数不一定能比较大小!
思考: 复数可以比大小吗?
例1:说出下列复数的实部和虚部,并判断它们是实数,虚数,还是纯虚数.
①2+3i; ② ;
③ ; ④π;
⑤ ; ⑥0.
二、例题讲解
类型一:复数的有关概念
练习:下列命题中,正确命题有_________
①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
④实数集是复数集的真子集
⑤实数集相对复数集的补集是虚数集
类型一:复数的有关概念
④⑤
例2:当实数m为何值时,z=m2-m-6+(m2+5m+6)i是:
(1)虚数; (2)纯虚数;
(3)实数.
类型二:复数的分类
练习:当实数k为何值时,z=(1+i)k2-(3+5i)k-2(2+3i)是:
(1)实数; (2)虚数;
(3)纯虚数;
类型二:复数的分类
解: 由z=(1+i)k2-(3+5i)k-2(2+3i)=(k2-3k-4)+(k2-5k-6)i.
(1)当k2-5k-6=0,
(2)当k2-5k-6≠0,
即k=6或k=-1时,z是实数;
即k≠6且k≠-1时,z是虚数;
练习:当实数k为何值时,z=(1+i)k2-(3+5i)k-2(2+3i)是:
(1)实数; (2)虚数;
(3)纯虚数;
类型二:复数的分类
解: 由z=(1+i)k2-(3+5i)k-2(2+3i)=(k2-3k-4)+(k2-5k-6)i.
(3)当 时,z是纯虚数,解得k=4.
解: 由z=(1+i)k2-(3+5i)k-2(2+3i)=(k2-3k-4)+(k2-5k-6)i.
(4)当 时,z=0,解得k=-1.
类型三:复数相等
例3:当实数k为何值时,z=(1+i)k2-(3+5i)k-2(2+3i)是:
(1)实数; (2)虚数;
(3)纯虚数;
(4)零.
类型三:复数相等
练习:若xi-i2=y+2i,x,y∈R,则复数x+yi=______
2+i
三、当堂检测
1.给出下列说法:
①复数2+3i的虚部是3i;
②形如a+bi(b∈R)的数一定是虚数;
③若实数a与ai对应,则实数集与纯虚数集--对应;
④若a∈R,则(a+1)i是纯虚数;
⑤若x是实数,则x可能不是复数;
其中说法不正确的是_________.
①②③④⑤
四、当堂检测
3.若复数z=ai2-bi (x,y∈R)是纯虚数,则一定有( )
A.b=0 B.a=0且b≠0 C.a=0或b=0 D.ab≠0
B
2.当实数m为何值时,z= +(m2+5m+6)i是:
(1)虚数; (2)纯虚数;
(3)实数.
四、素养提升
数学运算——转化思想在复数中的应用
思考:
归纳小结
1.虚数单位i的引入、数系的扩充
归纳小结
2.复数的有关概念
作业
第七章 复数
7.1 复数的概念
7.1.1 数系的扩充和复数的概念
计数的需要
自然数
被“数”出来的自然数
自然数是现实世界最基本的数量,是全部数学的发源地.
回顾历史,发现扩充规则
相反量的需要
负数
被“欠”出来的负数
负数的引入,解决了在数集中不够减的矛盾.
吐鲁番盆地大约比海平面低155米.
+8844
-155
珠穆朗玛峰大约比海平面高8844米.
等额公平分配的需要
分数
被“分”出来的分数
分数的引入,解决了在整数中不能整除的矛盾.
度量计算的需要
无理数
1
1
边长为1的正方形的对角线长是多少
被“推”出来的无理数
无理数的引入解决了开方开不尽的矛盾.
?
很多方程没有根
代数
几何
问题:求下列方程的解
核心问题:
引进一个新数,使 类方程有解,并将数系
进一步扩充。
一、新知探究
引入一个新数
1777年,欧拉首次提出用i表示平方等于-1的新数
1801年,高斯系统使用了i这个符号,使之通行于世
新数集
问题:用数i,1,2,这三个数中的若干个进行加法乘法运算,能写出哪些式子?
(1)形如 的数叫做复数,通常用字母 z 表示.
(2)全体复数所形成的集合叫做复数集,一般用C 表示.
实部
虚部
1 、复数的概念
虚数单位,i2=-1
思考:复数集与实数集具有什么关系呢?
2 、复数的分类
实数R
纯虚数
虚数
复数集C
3 、复数相等
规定:
复数不一定能比较大小!
思考: 复数可以比大小吗?
例1:说出下列复数的实部和虚部,并判断它们是实数,虚数,还是纯虚数.
①2+3i; ② ;
③ ; ④π;
⑤ ; ⑥0.
二、例题讲解
类型一:复数的有关概念
练习:下列命题中,正确命题有_________
①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
④实数集是复数集的真子集
⑤实数集相对复数集的补集是虚数集
类型一:复数的有关概念
④⑤
例2:当实数m为何值时,z=m2-m-6+(m2+5m+6)i是:
(1)虚数; (2)纯虚数;
(3)实数.
类型二:复数的分类
练习:当实数k为何值时,z=(1+i)k2-(3+5i)k-2(2+3i)是:
(1)实数; (2)虚数;
(3)纯虚数;
类型二:复数的分类
解: 由z=(1+i)k2-(3+5i)k-2(2+3i)=(k2-3k-4)+(k2-5k-6)i.
(1)当k2-5k-6=0,
(2)当k2-5k-6≠0,
即k=6或k=-1时,z是实数;
即k≠6且k≠-1时,z是虚数;
练习:当实数k为何值时,z=(1+i)k2-(3+5i)k-2(2+3i)是:
(1)实数; (2)虚数;
(3)纯虚数;
类型二:复数的分类
解: 由z=(1+i)k2-(3+5i)k-2(2+3i)=(k2-3k-4)+(k2-5k-6)i.
(3)当 时,z是纯虚数,解得k=4.
解: 由z=(1+i)k2-(3+5i)k-2(2+3i)=(k2-3k-4)+(k2-5k-6)i.
(4)当 时,z=0,解得k=-1.
类型三:复数相等
例3:当实数k为何值时,z=(1+i)k2-(3+5i)k-2(2+3i)是:
(1)实数; (2)虚数;
(3)纯虚数;
(4)零.
类型三:复数相等
练习:若xi-i2=y+2i,x,y∈R,则复数x+yi=______
2+i
三、当堂检测
1.给出下列说法:
①复数2+3i的虚部是3i;
②形如a+bi(b∈R)的数一定是虚数;
③若实数a与ai对应,则实数集与纯虚数集--对应;
④若a∈R,则(a+1)i是纯虚数;
⑤若x是实数,则x可能不是复数;
其中说法不正确的是_________.
①②③④⑤
四、当堂检测
3.若复数z=ai2-bi (x,y∈R)是纯虚数,则一定有( )
A.b=0 B.a=0且b≠0 C.a=0或b=0 D.ab≠0
B
2.当实数m为何值时,z= +(m2+5m+6)i是:
(1)虚数; (2)纯虚数;
(3)实数.
四、素养提升
数学运算——转化思想在复数中的应用
思考:
归纳小结
1.虚数单位i的引入、数系的扩充
归纳小结
2.复数的有关概念
作业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
