沪科版数学七年级下册 9.2.2 第2课时 分式的加减课件 (27张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 9.2.2 第2课时 分式的加减课件 (27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 22:40:10 | ||
图片预览




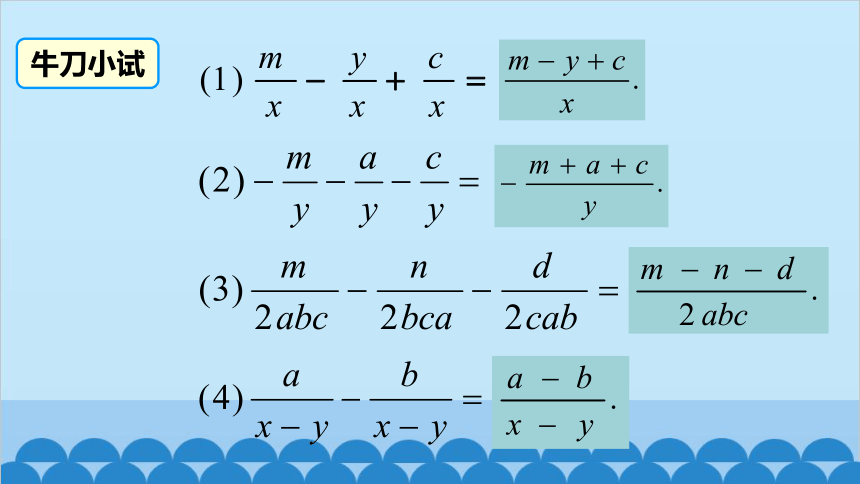


文档简介
(共27张PPT)
2.分式的加减
第9章 分 式
第2课时 分式的加减
9.2 分式的运算
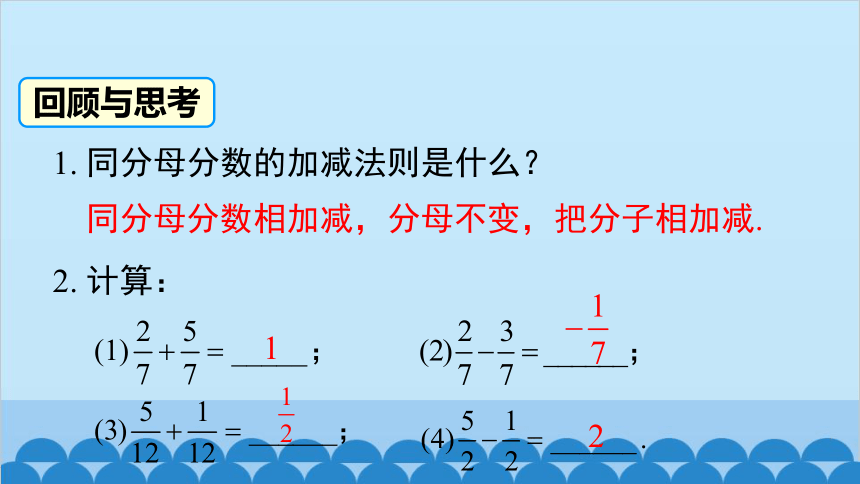
1. 同分母分数的加减法则是什么?
1
2. 计算:
2
同分母分数相加减,分母不变,把分子相加减.
回顾与思考
思考:类比前面同分母分数的加减,想想下面的式子该怎么计算?
a
1
a
2
+
想一想:同分母的分式应该如何加减?
类比探究
观察下列分数加减运算的式子,你想到了什么?
请类比同分母分数的加减法,说一说同分母的分式应该如何加减.
同分母分式的加减
知识要点
同分母分式的加减法则
同分母分式相加减,分母不变,分子相加减.
上述法则可用式子表示为
牛刀小试
解:原式 =
=
=
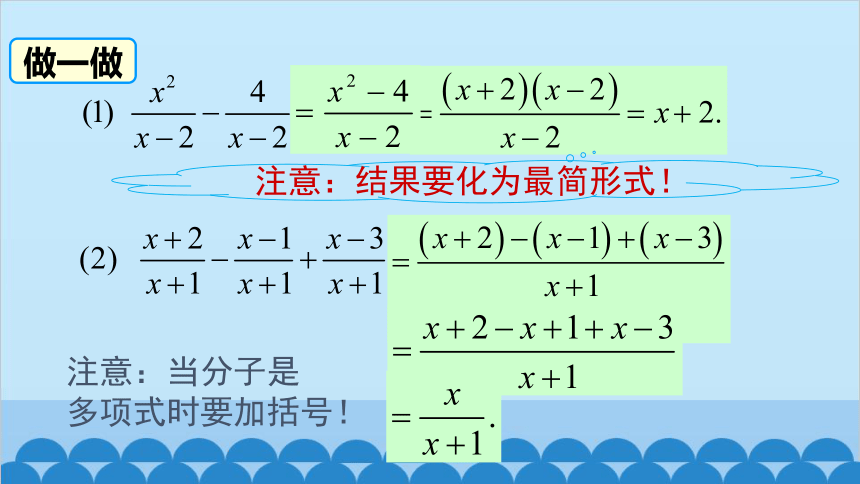
注意:结果要化为最简分式!
=
例1 计算:
典例精析
解:原式 =
=
=
注意:结果要化为最简分式!
=
把分子看作一个整体,先用括号括起来!
去括号
合并同类项
注意:结果要化为最简形式!
做一做
注意:当分子是
多项式时要加括号!
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
异分母分式的加减
请计算 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
请思考
b
d
b
d
类比:异分母的分式应该如何加减
知识要点
异分母分式的加减法则
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法则进行计算.
上述法则可用式子表示为
解:原式 =
=
=
注意:(1 - x) = -(x - 1)
例2 计算:
分母不同,先化为同分母.
解:原式 =
先找出最简公分母,再正确通分,转化为同分母分式的加减
解:原式 =
=
=
注:分母是多项式的先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
=
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
例3 计算:
法一:
原式 =
法二:
原式 =
把整式看成分母为“1”的式子
阅读下面的计算过程:
①
= ②
= ③
= ④
(1) 上述计算过程,从哪一步开始出错?请写出
该步的代号_____;
(2) 错误原因是___________;
(3) 本题的正确结果为: .
②
漏掉了分母
做一做
例4 计算:
解:原式
从 -3,1,3 中任选一个 m 值代入求值.
当 m = 1 时,原式
先化简,再求值: ,其中 .
解:
做一做
例5 已知下面一列等式:
(1) 请你根据这些等式的结构特征写出它的一般性等式;
(2) 验证你写出的等式是否成立;
(3) 利用等式计算:
①;
②;
③;
④.
解析:(1) 观察已知的四个等式,发现等式的左边是两个分数之积,这两个分数的分子都是 1,后一个分数的分母比前一个分数的分母大 1,并且第一个分数的分母与等式的序号相等,等式的右边是这两个分数之差,据此可写出一般性等式;
(2) 根据分式的运算法则验证即可;
(3) 根据(1)中的结论求解.
.
(2)因为
.
所以
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2. 填空:
4
3. 计算:
解:(1) 原式 =
(2) 原式 =
4. 先化简,再求值: ,其中 x = 2023.
当 x = 2023 时,原式
分式加减运算
加减运算法则
注意点
异分母分式相加减先转化为同分母分式的加减运算
(2) 整式和分式之间进行加减运算时,则要把整式看成分母是 1 的式子,以便通分
(3) 异分母分式进行加减运算需要先通分,关键是确定最简公分母
(1) 若分式作为减式,则运算时要注意适时添加括号
2.分式的加减
第9章 分 式
第2课时 分式的加减
9.2 分式的运算
1. 同分母分数的加减法则是什么?
1
2. 计算:
2
同分母分数相加减,分母不变,把分子相加减.
回顾与思考
思考:类比前面同分母分数的加减,想想下面的式子该怎么计算?
a
1
a
2
+
想一想:同分母的分式应该如何加减?
类比探究
观察下列分数加减运算的式子,你想到了什么?
请类比同分母分数的加减法,说一说同分母的分式应该如何加减.
同分母分式的加减
知识要点
同分母分式的加减法则
同分母分式相加减,分母不变,分子相加减.
上述法则可用式子表示为
牛刀小试
解:原式 =
=
=
注意:结果要化为最简分式!
=
例1 计算:
典例精析
解:原式 =
=
=
注意:结果要化为最简分式!
=
把分子看作一个整体,先用括号括起来!
去括号
合并同类项
注意:结果要化为最简形式!
做一做
注意:当分子是
多项式时要加括号!
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
异分母分式的加减
请计算 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
请思考
b
d
b
d
类比:异分母的分式应该如何加减
知识要点
异分母分式的加减法则
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法则进行计算.
上述法则可用式子表示为
解:原式 =
=
=
注意:(1 - x) = -(x - 1)
例2 计算:
分母不同,先化为同分母.
解:原式 =
先找出最简公分母,再正确通分,转化为同分母分式的加减
解:原式 =
=
=
注:分母是多项式的先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
=
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
例3 计算:
法一:
原式 =
法二:
原式 =
把整式看成分母为“1”的式子
阅读下面的计算过程:
①
= ②
= ③
= ④
(1) 上述计算过程,从哪一步开始出错?请写出
该步的代号_____;
(2) 错误原因是___________;
(3) 本题的正确结果为: .
②
漏掉了分母
做一做
例4 计算:
解:原式
从 -3,1,3 中任选一个 m 值代入求值.
当 m = 1 时,原式
先化简,再求值: ,其中 .
解:
做一做
例5 已知下面一列等式:
(1) 请你根据这些等式的结构特征写出它的一般性等式;
(2) 验证你写出的等式是否成立;
(3) 利用等式计算:
①;
②;
③;
④.
解析:(1) 观察已知的四个等式,发现等式的左边是两个分数之积,这两个分数的分子都是 1,后一个分数的分母比前一个分数的分母大 1,并且第一个分数的分母与等式的序号相等,等式的右边是这两个分数之差,据此可写出一般性等式;
(2) 根据分式的运算法则验证即可;
(3) 根据(1)中的结论求解.
.
(2)因为
.
所以
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2. 填空:
4
3. 计算:
解:(1) 原式 =
(2) 原式 =
4. 先化简,再求值: ,其中 x = 2023.
当 x = 2023 时,原式
分式加减运算
加减运算法则
注意点
异分母分式相加减先转化为同分母分式的加减运算
(2) 整式和分式之间进行加减运算时,则要把整式看成分母是 1 的式子,以便通分
(3) 异分母分式进行加减运算需要先通分,关键是确定最简公分母
(1) 若分式作为减式,则运算时要注意适时添加括号
