人教版小学数学四下平均数与条形统计图作业(含解析)
文档属性
| 名称 | 人教版小学数学四下平均数与条形统计图作业(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 269.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 00:00:00 | ||
图片预览




文档简介
小学数学四下平均数与条形统计图作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.四(1)班男生的平均体重是34千克,女生的平均体重是30千克,四(1)班全班同学的平均体重是( )。
A.32千克 B.31千克 C.无法确定
2.下面的统计图中,虚线所在位置能反映这三个数的平均数的图是( )。
A. B. C.
3.张欢数学英语的平均分是92分,其中英语90分,数学( )分。
A.92 B.94 C.90
4.哥哥有零钱27元,妹妹有零钱11元。哥哥给( )元妹妹,两人的钱一样多。
A.16 B.6 C.8
5.两个小组同时生产一批玩具,5天做完,第一小组生产了100个,第二小组生产了150个,第一小组比第二小组平均每天少生产多少个?正确的算式是( )。
A.150×5-100×5 B.150÷5-100÷5
C.(150×100)×5 D.(150+100)÷5
二、填空题
6.3个连续自然数的平均数是23,这3个自然数中,最小的是( ),最大的是( )。
7.姐姐用电脑打字前2分钟打了242个字,第3分钟打了148个字,姐姐这3分钟平均每分钟打( )个字。
8.下面是某水果店一周销售苹果、香蕉、桔子三种水果情况统计图。请看图填空。
(1)一周中,销售量最大的水果是( ),销售量最小的水果是( ),两种水果销售量相差( )千克。
(2)一周中,三种水果共销售( )千克,平均每种水果销售( )千克。
9.东东12岁,欢欢10岁,明明14岁,他们三个人的平均年龄是( )岁。
10.某乡村小学2021年一年级新招学生中,男生有86人,女生有78人,编成4个班。求平均每班有多少人,应用了( )法和( )法。
三、判断题
11.1,5,5,5,4,4,4,这组数据中有两个众数,5和4。 ( )
12.一个池塘中的平均水深是1米,这个池塘中一定没有比2米深的地方。( )
13.平均数和平均分一样。( )
14.小米所在班级的平均身高是145厘米,小浩所在班级的平均身高是143厘米,所以小米一定比小浩高。( )
15.复式统计表只能把两个统计项目的数据合并在一张表上。( )
16.横向条形统计图和纵向条形统计图只是形式上不同,当数据的种类不多或数据较大时,用横向条形统计图表示更为简便。( )
四、计算题
17.五个连续自然数的和是135,这五个连续自然数分别是多少?
五、解答题
18.找出3,2,1,6,9,5的中位数。
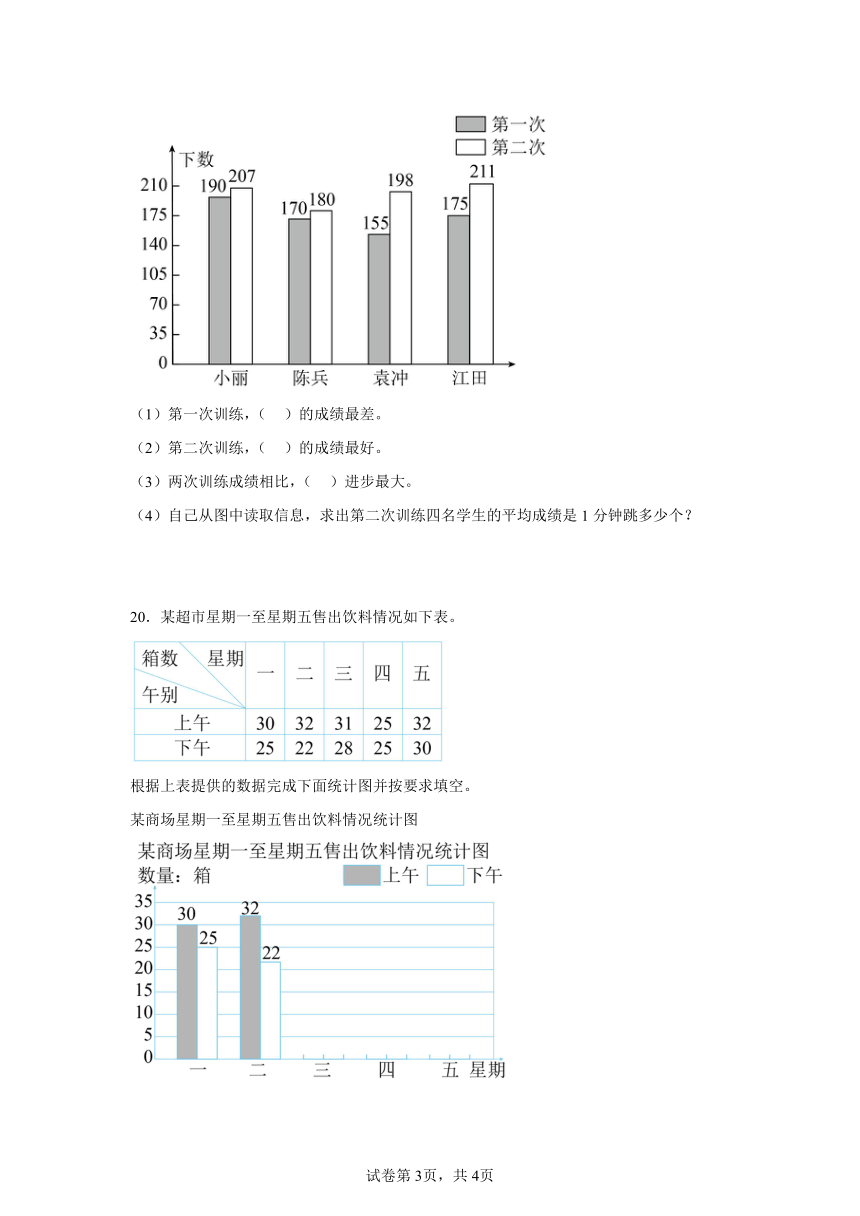
19.四(1)班要选一名学生代表班级参加学校四年级一分钟跳绳比赛,班主任老师预选四名学生进行训练,两次的训练成绩如图。
(1)第一次训练,( )的成绩最差。
(2)第二次训练,( )的成绩最好。
(3)两次训练成绩相比,( )进步最大。
(4)自己从图中读取信息,求出第二次训练四名学生的平均成绩是1分钟跳多少个?
20.某超市星期一至星期五售出饮料情况如下表。
根据上表提供的数据完成下面统计图并按要求填空。
某商场星期一至星期五售出饮料情况统计图
(1)条形表示( ),条形表示( )。
(2)星期一共售出饮料( )箱,星期三共售出饮料( )箱。
(3)星期一至星期五下午一共售出饮料( )箱,平均每天下午售出饮料( )箱。
(4)一天中,售出饮料最多的是星期( ),售出饮料最少的是星期( )。
21.2023年5月30日,神舟十六号航天员顺利进驻中国空间站,六名航天员实现“太空会师”。神舟十五号3名航天员的平均年龄是53岁,神舟十六号3名航天员的平均年龄是43岁,那6人的平均年龄是多少岁?
22.下图是某年韶关、江门两市各季度平均气温统计图。
请你根据上图回答下面的问题。
(1)第一季度江门市平均气温是( )摄氏度。
(2)上图中每格代表( )摄氏度。
(3)两地平均气温最接近的是第( )季度,平均气温差距最大的是第( )季度。
(4)第四季度江门市平均气温比韶关市平均气温高了( )摄氏度。
(5)江门市全年平均每月气温是多少摄氏度?(列式计算)
23.洛阳地铁1号线五一期间单日客运量如下表所示:
日期 5月1日 5月2日 5月3日 5月4日 5月5日
客运量(万人次) 15.3 16.4 19.6 24.6 19.1
洛阳地铁1号线五一期间平均每天客运量多少万人次?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据平均数的计算方法:总数÷份数=平均数,题中分别已知男生和女生的平均体重,但不知道男生和女生的人数,无法确定总体重和总人数,因此无法求出全班同学的平均体重。据此选择。
【详解】根据分析可知:
四(1)班全班同学的平均体重无法确定。
故答案为:C
2.B
【分析】从三个图中可知:从上往下,第一个数最小,第二个数最大,第三个数居中;可以利用移多补少的方法,以虚线位置为界限,用三个数中多的部分去填补少的部分,基本达到三个数都与虚线位置一致,则说明虚线的位置能反映这三个数的平均数。据此解答。
【详解】A.第一个数比虚线位置少一点,第二个数和第三个数都比虚线位置多很多,如果用第二三个数多的部分去填补第一个数少的部分,会使第一个数超过虚线位置,所以此虚线位置不能反映三个数的平均数;
B.第一个数和第三个数比虚线位置都少一些,第二个数比虚线位置多很多,如果用第二个数多的部分去填补第一三个数少的部分,基本可以让三个数都达到虚线位置,所以此虚线位置能反映三个数的平均数;
C.第一个数比虚线位置少一些,第二个数比虚线位置多很多,第三个数等于虚线位置,如果用第二个数多的部分去填补第一个数少的部分,会使第一个数超过虚线位置,所以此虚线位置不能反映三个数的平均数。
所以,虚线所在位置能反映这三个数的平均数的图是。
故答案为:B
3.B
【分析】先用92乘2计算出数学和英语的总成绩,再减去英语成绩,计算出数学成绩;据此解答。
【详解】根据分析:
92×2-90
=184-90
=94(分)
所以数学94分。
故答案为:B
4.C
【分析】根据题意可知,先用减法计算出哥哥和妹妹的零钱差,然后再除以2即可,依此解答。
【详解】(27-11)÷2
=16÷2
=8(元)
哥哥给8元妹妹,两人的钱一样多。
故答案为:C
5.B
【分析】由题意,用第二小组生产的个数除以天数,求出第二小组平均每天生产玩具的个数,同理求出第一小组平均每天生产玩具的个数,再相减,即得第一小组比第二小组平均每天少生产多少个。
【详解】150÷5-100÷5
=30-20
=10(个)
第一小组比第二小组平均每天少生产10个。
故答案为:B
6. 22 24
【分析】3个连续自然数的平均数是23,即23就是3个自然数中间的那个数,因为相邻的两个自然数相差1,所以最小的自然数是23-1,最大的自然数是23+1,据此作答。
【详解】23-1=22
23+1=24
所以,3个自然数中,最小的是22,最大的是24。
7.130
【分析】先用242加上148计算出3分钟打的总字数,再除以3计算出姐姐这3分钟平均每分钟打多少个字;据此解答。
【详解】(242+148)÷3
=390÷3
=130(个)
所以姐姐这3分钟平均每分钟打130个字。
8.(1) 苹果 桔子 75
(2) 1074 358
【分析】(1)比较一周中销售苹果、香蕉、桔子三种水果的千克数即可得出结论;求两种水果销售量相差多少千克,用减法解答;
(2)把一周中销售苹果、香蕉、桔子三种水果的千克数相加求和即可;用三种水果共销售的总质量除以3,即可求得平均每种水果销售多少千克。
【详解】(1)390>369>315
一周中,销售量最大的水果是苹果,销售量最小的水果是桔子,
390-315=75(千克)
两种水果销售量相差75千克。
(2)315+369+390
=684+390
=1074(千克)
1074÷3=358(千克)
一周中,三种水果共销售1074千克,平均每种水果销售358千克。
9.12
【分析】根据“平均年龄=三个人的年龄和÷总人数”代入数据解答即可。
【详解】(12+10+14)÷3
=36÷3
=12(岁)
他们三个人的平均年龄是12岁。
10. 加 除
【分析】根据平均数=总数÷总份数,一年级新招的学生总人数就是男生的人数加上女生的人数,编成4个班,再用总的学生人数除以4,就是平均每班的人数。据此解答即可。
【详解】(86+78)÷4
=164÷4
=41(人)
计算过程中应用了加法和除法。
11.√
【分析】一组数据中出现次数最多的数叫做这组数据的众数,据此找出这组数据中的众数即可。
【详解】这组数据中有1个1、3个4和3个5,4和5的个数最多且相同,所以这组数据中有两个众数,5和4。
故答案为:√
【点睛】
12.×
【分析】平均数只能反映一组数据的平均水平,并不能反映这组数据的中所有数据的大小,一个池塘中的平均水深是1米,可能有的地方水深超过1米很多,甚至超过2米,据此判断。
【详解】因为平均数不能反映这组数据的中所有数据的大小,所以一个池塘中的平均水深是1米,这个池塘中可能有比2米深的地方。原说法错误。
故答案为:×
13.×
【分析】平均分是指把一组数据分成若干份,每份的数量都相等;平均数是指把一组数据若干等分后,每组数据的数量是多少。
【详解】根据分析可知,平均数和平均分是不一样的,原题说法错误。
故答案为:×
14.×
【分析】根据平均数的意义知道平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。小米所在班级的平均身高是145厘米,并不是小米的身高就是145厘米,她的身高有可能比145厘米高,也可能比145厘米矮,同样的道理小浩所在班级的平均身高是143厘米,并不是说小浩的身高就是143厘米,由此即可得出判断。
【详解】小米所在班级的平均身高是145厘米,小浩所在班级的平均身高是143厘米,但是小浩也有可能比小米高,原题干说法错误。
故答案为:×。
【点睛】本题主要考查了平均数的意义的理解,平均数反映的是一组数据的特征,不是一个数据的特征。
15.×
【分析】根据复式统计表的定义即可进行判断正误。
【详解】复式统计表能把两个(或多个)统计内容的数据合并在一张表上,可以更加清晰、明了地反映数据的情况,原题说法错误。
故答案为:×
16.√
【详解】条形统计图根据直条的方向可以分为横向条形统计图和纵向条形统计图。一般在数据种类较多,数据又不是非常大时使用纵向条形统计图;在数据种类较少,每类数据又比较大时,使用横向条形统计图;所以判断正确。
17.25、26、27、28、29
【分析】中间的一个自然数是这五个连续自然数的平均数,先求出中间的自然数,再根据相邻两个自然数相差1求出其它的自然数;据此解答。
【详解】中间的自然数:135÷5=27
27-1=26,26-1=25,27+1=28,28+1=29
所以,这五个连续自然数分别是25、26、27、28、29。
18.4
【分析】将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数。
【详解】原数据由小达到排列是1,2,3,5,6,9,共6个是偶数个,中间的两个数是3和5,(3+5)÷2=4,所以这组数据的中位数是4。
19.(1)袁冲
(2)江田
(3)袁冲
(4)199个
【分析】(1)把第一次四名学生的训练成绩进行比较,即可解答;
(2)把第二次四名学生的训练成绩进行比较,即可解答;
(3)分别用每名学生第二次训练的成绩减去第一次训练的成绩,求出每个人增长进步的成绩,然后再比较成绩即可解答;
(4)把第二次训练四名学生的成绩相加,求出四名学生第二次训练的总成绩,再用四名学生第二次训练的总成绩除以4,即可求出第二次训练四名学生的平均成绩是1分钟跳多少个。
【详解】(1)155<170<175<190
第一次训练,袁冲的成绩最差。
(2)211>207>198>180
第二次训练,江田的成绩最好。
(3)小丽:207-190=17
陈兵:180-170=10
袁冲:198-155=43
江田:211-175=36
10<17<36<43
两次训练成绩相比,袁冲进步最大。
(4)(207+180+198+211)÷4
=(387+198+211)÷4
=(585+211)÷4
=796÷4
=199(个)
答:第二次训练四名学生的平均成绩是1分钟跳199个。
20.统计图见详解;(1)上午销售的数量;下午销售的数量;(2)55;59;(3)130;26;(4)星期五;星期四
【分析】根据统计表提供的数据完成复式条形统计图即可。
(1)根据统计图可知,条形表示上午销售的数量,条形表示下午销售的数量。
(2)把星期一上午和下午销售的饮料箱数和星期三的上午和下午销售的饮料箱数分别相加,即可求出星期一共售出饮料的箱数,星期三共售出饮料的箱数。
(3)把星期一至星期五下午售出饮料的箱数相加,即可求出星期一至星期五下午一共售出饮料的箱数;用星期一至星期五下午一共售出饮料的箱数除以5,即可求出平均每天下午售出饮料的箱数。
(4)把星期一全天售出的饮料箱数至星期五全天售出的饮料箱数分别相加,然后再进行比较,即可求出售出饮料最多的是星期几,售出饮料最少的是星期几。
【详解】
(1)条形表示上午销售的数量,条形表示下午销售的数量。
(2)30+25=55(箱)
31+28=59(箱)
星期一共售出饮料55箱,星期三共售出饮料59箱。
(3)25+22+28+25+30
=47+28+25+30
=75+25+30
=100+30
=130(箱)
130÷5=26(箱)
星期一至星期五下午一共售出饮料130箱,平均每天下午售出饮料26箱。
(4)星期一:30+25=55(箱)
星期二:32+22=54(箱)
星期三:31+28=59(箱)
星期四:25+25=50(箱)
星期五:32+30=62(箱)
50<54<55<59<62
一天中,售出饮料最多的是星期五,售出饮料最少的是星期四。
21.48岁
【分析】根据总数=平均数×数量,用神舟十五号3名航天员的平均年龄乘人数、神舟十六号3名航天员的平均年龄乘人数,分别计算出总年龄,再将神舟十五号3名航天员和神舟十六号3名航天员的总年龄相加,即可求出6名航天员的总年龄,再除以6,即可求出6人的平均年龄是多少岁。
【详解】(53×3+43×3)÷6
=(159+129)÷6
=288÷6
=48(岁)
答:6人的平均年龄是48岁。
22.(1)17
(2)5
(3)三;四
(4)9
(5)24摄氏度
【分析】(1)根据统计图中的数据作答即可;
(2)观察纵轴统计图的数据,可知每格代表 5摄氏度。
(3)将每个季度的两地的平均气温作差,差最小的,那么这个季度两地平均气温最接近;差最大的,那么这个季度两地平均气温差距最大;
(4)把第四季度江门市平均气温比韶关市平均气温相减即可求得高了几度。
(5)将江门市全年平均气温加起来除以4即可解答。
【详解】(1)第一季度江门市平均气温是17摄氏度。
(2)上图中每格代表5摄氏度。
(3)第一季度:17-15=2(摄氏度)
第二季度:26-24=2(摄氏度)
第三季度:29-28=1(摄氏度)
第四季度:25-16=9(摄氏度)
两地平均气温最接近的是第三季度,平均气温差距最大的是第四季度。
(4)25-16=9(摄氏度)
第四季度江门市平均气温比韶关市平均气温高了9摄氏度。
(5)(17+26+28+25)÷4
=96÷4
=24(摄氏度)
答:江门市全年平均每月气温是24摄氏度。
23.19万人次
【分析】根据表格先求和算出5天的总客运量,再根据总数÷份数=每份数,即可求出。
【详解】(15.3+16.4+19.6+24.6+19.1)÷5
=(31.7+19.6+24.6+19.1)÷5
=(51.3+24.6+19.1)÷5
=(75.9+19.1)÷5
=95÷5
=19(万人次)
答:洛阳地铁1号线五一期间平均每天客运量19万人次。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.四(1)班男生的平均体重是34千克,女生的平均体重是30千克,四(1)班全班同学的平均体重是( )。
A.32千克 B.31千克 C.无法确定
2.下面的统计图中,虚线所在位置能反映这三个数的平均数的图是( )。
A. B. C.
3.张欢数学英语的平均分是92分,其中英语90分,数学( )分。
A.92 B.94 C.90
4.哥哥有零钱27元,妹妹有零钱11元。哥哥给( )元妹妹,两人的钱一样多。
A.16 B.6 C.8
5.两个小组同时生产一批玩具,5天做完,第一小组生产了100个,第二小组生产了150个,第一小组比第二小组平均每天少生产多少个?正确的算式是( )。
A.150×5-100×5 B.150÷5-100÷5
C.(150×100)×5 D.(150+100)÷5
二、填空题
6.3个连续自然数的平均数是23,这3个自然数中,最小的是( ),最大的是( )。
7.姐姐用电脑打字前2分钟打了242个字,第3分钟打了148个字,姐姐这3分钟平均每分钟打( )个字。
8.下面是某水果店一周销售苹果、香蕉、桔子三种水果情况统计图。请看图填空。
(1)一周中,销售量最大的水果是( ),销售量最小的水果是( ),两种水果销售量相差( )千克。
(2)一周中,三种水果共销售( )千克,平均每种水果销售( )千克。
9.东东12岁,欢欢10岁,明明14岁,他们三个人的平均年龄是( )岁。
10.某乡村小学2021年一年级新招学生中,男生有86人,女生有78人,编成4个班。求平均每班有多少人,应用了( )法和( )法。
三、判断题
11.1,5,5,5,4,4,4,这组数据中有两个众数,5和4。 ( )
12.一个池塘中的平均水深是1米,这个池塘中一定没有比2米深的地方。( )
13.平均数和平均分一样。( )
14.小米所在班级的平均身高是145厘米,小浩所在班级的平均身高是143厘米,所以小米一定比小浩高。( )
15.复式统计表只能把两个统计项目的数据合并在一张表上。( )
16.横向条形统计图和纵向条形统计图只是形式上不同,当数据的种类不多或数据较大时,用横向条形统计图表示更为简便。( )
四、计算题
17.五个连续自然数的和是135,这五个连续自然数分别是多少?
五、解答题
18.找出3,2,1,6,9,5的中位数。
19.四(1)班要选一名学生代表班级参加学校四年级一分钟跳绳比赛,班主任老师预选四名学生进行训练,两次的训练成绩如图。
(1)第一次训练,( )的成绩最差。
(2)第二次训练,( )的成绩最好。
(3)两次训练成绩相比,( )进步最大。
(4)自己从图中读取信息,求出第二次训练四名学生的平均成绩是1分钟跳多少个?
20.某超市星期一至星期五售出饮料情况如下表。
根据上表提供的数据完成下面统计图并按要求填空。
某商场星期一至星期五售出饮料情况统计图
(1)条形表示( ),条形表示( )。
(2)星期一共售出饮料( )箱,星期三共售出饮料( )箱。
(3)星期一至星期五下午一共售出饮料( )箱,平均每天下午售出饮料( )箱。
(4)一天中,售出饮料最多的是星期( ),售出饮料最少的是星期( )。
21.2023年5月30日,神舟十六号航天员顺利进驻中国空间站,六名航天员实现“太空会师”。神舟十五号3名航天员的平均年龄是53岁,神舟十六号3名航天员的平均年龄是43岁,那6人的平均年龄是多少岁?
22.下图是某年韶关、江门两市各季度平均气温统计图。
请你根据上图回答下面的问题。
(1)第一季度江门市平均气温是( )摄氏度。
(2)上图中每格代表( )摄氏度。
(3)两地平均气温最接近的是第( )季度,平均气温差距最大的是第( )季度。
(4)第四季度江门市平均气温比韶关市平均气温高了( )摄氏度。
(5)江门市全年平均每月气温是多少摄氏度?(列式计算)
23.洛阳地铁1号线五一期间单日客运量如下表所示:
日期 5月1日 5月2日 5月3日 5月4日 5月5日
客运量(万人次) 15.3 16.4 19.6 24.6 19.1
洛阳地铁1号线五一期间平均每天客运量多少万人次?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】根据平均数的计算方法:总数÷份数=平均数,题中分别已知男生和女生的平均体重,但不知道男生和女生的人数,无法确定总体重和总人数,因此无法求出全班同学的平均体重。据此选择。
【详解】根据分析可知:
四(1)班全班同学的平均体重无法确定。
故答案为:C
2.B
【分析】从三个图中可知:从上往下,第一个数最小,第二个数最大,第三个数居中;可以利用移多补少的方法,以虚线位置为界限,用三个数中多的部分去填补少的部分,基本达到三个数都与虚线位置一致,则说明虚线的位置能反映这三个数的平均数。据此解答。
【详解】A.第一个数比虚线位置少一点,第二个数和第三个数都比虚线位置多很多,如果用第二三个数多的部分去填补第一个数少的部分,会使第一个数超过虚线位置,所以此虚线位置不能反映三个数的平均数;
B.第一个数和第三个数比虚线位置都少一些,第二个数比虚线位置多很多,如果用第二个数多的部分去填补第一三个数少的部分,基本可以让三个数都达到虚线位置,所以此虚线位置能反映三个数的平均数;
C.第一个数比虚线位置少一些,第二个数比虚线位置多很多,第三个数等于虚线位置,如果用第二个数多的部分去填补第一个数少的部分,会使第一个数超过虚线位置,所以此虚线位置不能反映三个数的平均数。
所以,虚线所在位置能反映这三个数的平均数的图是。
故答案为:B
3.B
【分析】先用92乘2计算出数学和英语的总成绩,再减去英语成绩,计算出数学成绩;据此解答。
【详解】根据分析:
92×2-90
=184-90
=94(分)
所以数学94分。
故答案为:B
4.C
【分析】根据题意可知,先用减法计算出哥哥和妹妹的零钱差,然后再除以2即可,依此解答。
【详解】(27-11)÷2
=16÷2
=8(元)
哥哥给8元妹妹,两人的钱一样多。
故答案为:C
5.B
【分析】由题意,用第二小组生产的个数除以天数,求出第二小组平均每天生产玩具的个数,同理求出第一小组平均每天生产玩具的个数,再相减,即得第一小组比第二小组平均每天少生产多少个。
【详解】150÷5-100÷5
=30-20
=10(个)
第一小组比第二小组平均每天少生产10个。
故答案为:B
6. 22 24
【分析】3个连续自然数的平均数是23,即23就是3个自然数中间的那个数,因为相邻的两个自然数相差1,所以最小的自然数是23-1,最大的自然数是23+1,据此作答。
【详解】23-1=22
23+1=24
所以,3个自然数中,最小的是22,最大的是24。
7.130
【分析】先用242加上148计算出3分钟打的总字数,再除以3计算出姐姐这3分钟平均每分钟打多少个字;据此解答。
【详解】(242+148)÷3
=390÷3
=130(个)
所以姐姐这3分钟平均每分钟打130个字。
8.(1) 苹果 桔子 75
(2) 1074 358
【分析】(1)比较一周中销售苹果、香蕉、桔子三种水果的千克数即可得出结论;求两种水果销售量相差多少千克,用减法解答;
(2)把一周中销售苹果、香蕉、桔子三种水果的千克数相加求和即可;用三种水果共销售的总质量除以3,即可求得平均每种水果销售多少千克。
【详解】(1)390>369>315
一周中,销售量最大的水果是苹果,销售量最小的水果是桔子,
390-315=75(千克)
两种水果销售量相差75千克。
(2)315+369+390
=684+390
=1074(千克)
1074÷3=358(千克)
一周中,三种水果共销售1074千克,平均每种水果销售358千克。
9.12
【分析】根据“平均年龄=三个人的年龄和÷总人数”代入数据解答即可。
【详解】(12+10+14)÷3
=36÷3
=12(岁)
他们三个人的平均年龄是12岁。
10. 加 除
【分析】根据平均数=总数÷总份数,一年级新招的学生总人数就是男生的人数加上女生的人数,编成4个班,再用总的学生人数除以4,就是平均每班的人数。据此解答即可。
【详解】(86+78)÷4
=164÷4
=41(人)
计算过程中应用了加法和除法。
11.√
【分析】一组数据中出现次数最多的数叫做这组数据的众数,据此找出这组数据中的众数即可。
【详解】这组数据中有1个1、3个4和3个5,4和5的个数最多且相同,所以这组数据中有两个众数,5和4。
故答案为:√
【点睛】
12.×
【分析】平均数只能反映一组数据的平均水平,并不能反映这组数据的中所有数据的大小,一个池塘中的平均水深是1米,可能有的地方水深超过1米很多,甚至超过2米,据此判断。
【详解】因为平均数不能反映这组数据的中所有数据的大小,所以一个池塘中的平均水深是1米,这个池塘中可能有比2米深的地方。原说法错误。
故答案为:×
13.×
【分析】平均分是指把一组数据分成若干份,每份的数量都相等;平均数是指把一组数据若干等分后,每组数据的数量是多少。
【详解】根据分析可知,平均数和平均分是不一样的,原题说法错误。
故答案为:×
14.×
【分析】根据平均数的意义知道平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。小米所在班级的平均身高是145厘米,并不是小米的身高就是145厘米,她的身高有可能比145厘米高,也可能比145厘米矮,同样的道理小浩所在班级的平均身高是143厘米,并不是说小浩的身高就是143厘米,由此即可得出判断。
【详解】小米所在班级的平均身高是145厘米,小浩所在班级的平均身高是143厘米,但是小浩也有可能比小米高,原题干说法错误。
故答案为:×。
【点睛】本题主要考查了平均数的意义的理解,平均数反映的是一组数据的特征,不是一个数据的特征。
15.×
【分析】根据复式统计表的定义即可进行判断正误。
【详解】复式统计表能把两个(或多个)统计内容的数据合并在一张表上,可以更加清晰、明了地反映数据的情况,原题说法错误。
故答案为:×
16.√
【详解】条形统计图根据直条的方向可以分为横向条形统计图和纵向条形统计图。一般在数据种类较多,数据又不是非常大时使用纵向条形统计图;在数据种类较少,每类数据又比较大时,使用横向条形统计图;所以判断正确。
17.25、26、27、28、29
【分析】中间的一个自然数是这五个连续自然数的平均数,先求出中间的自然数,再根据相邻两个自然数相差1求出其它的自然数;据此解答。
【详解】中间的自然数:135÷5=27
27-1=26,26-1=25,27+1=28,28+1=29
所以,这五个连续自然数分别是25、26、27、28、29。
18.4
【分析】将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数。
【详解】原数据由小达到排列是1,2,3,5,6,9,共6个是偶数个,中间的两个数是3和5,(3+5)÷2=4,所以这组数据的中位数是4。
19.(1)袁冲
(2)江田
(3)袁冲
(4)199个
【分析】(1)把第一次四名学生的训练成绩进行比较,即可解答;
(2)把第二次四名学生的训练成绩进行比较,即可解答;
(3)分别用每名学生第二次训练的成绩减去第一次训练的成绩,求出每个人增长进步的成绩,然后再比较成绩即可解答;
(4)把第二次训练四名学生的成绩相加,求出四名学生第二次训练的总成绩,再用四名学生第二次训练的总成绩除以4,即可求出第二次训练四名学生的平均成绩是1分钟跳多少个。
【详解】(1)155<170<175<190
第一次训练,袁冲的成绩最差。
(2)211>207>198>180
第二次训练,江田的成绩最好。
(3)小丽:207-190=17
陈兵:180-170=10
袁冲:198-155=43
江田:211-175=36
10<17<36<43
两次训练成绩相比,袁冲进步最大。
(4)(207+180+198+211)÷4
=(387+198+211)÷4
=(585+211)÷4
=796÷4
=199(个)
答:第二次训练四名学生的平均成绩是1分钟跳199个。
20.统计图见详解;(1)上午销售的数量;下午销售的数量;(2)55;59;(3)130;26;(4)星期五;星期四
【分析】根据统计表提供的数据完成复式条形统计图即可。
(1)根据统计图可知,条形表示上午销售的数量,条形表示下午销售的数量。
(2)把星期一上午和下午销售的饮料箱数和星期三的上午和下午销售的饮料箱数分别相加,即可求出星期一共售出饮料的箱数,星期三共售出饮料的箱数。
(3)把星期一至星期五下午售出饮料的箱数相加,即可求出星期一至星期五下午一共售出饮料的箱数;用星期一至星期五下午一共售出饮料的箱数除以5,即可求出平均每天下午售出饮料的箱数。
(4)把星期一全天售出的饮料箱数至星期五全天售出的饮料箱数分别相加,然后再进行比较,即可求出售出饮料最多的是星期几,售出饮料最少的是星期几。
【详解】
(1)条形表示上午销售的数量,条形表示下午销售的数量。
(2)30+25=55(箱)
31+28=59(箱)
星期一共售出饮料55箱,星期三共售出饮料59箱。
(3)25+22+28+25+30
=47+28+25+30
=75+25+30
=100+30
=130(箱)
130÷5=26(箱)
星期一至星期五下午一共售出饮料130箱,平均每天下午售出饮料26箱。
(4)星期一:30+25=55(箱)
星期二:32+22=54(箱)
星期三:31+28=59(箱)
星期四:25+25=50(箱)
星期五:32+30=62(箱)
50<54<55<59<62
一天中,售出饮料最多的是星期五,售出饮料最少的是星期四。
21.48岁
【分析】根据总数=平均数×数量,用神舟十五号3名航天员的平均年龄乘人数、神舟十六号3名航天员的平均年龄乘人数,分别计算出总年龄,再将神舟十五号3名航天员和神舟十六号3名航天员的总年龄相加,即可求出6名航天员的总年龄,再除以6,即可求出6人的平均年龄是多少岁。
【详解】(53×3+43×3)÷6
=(159+129)÷6
=288÷6
=48(岁)
答:6人的平均年龄是48岁。
22.(1)17
(2)5
(3)三;四
(4)9
(5)24摄氏度
【分析】(1)根据统计图中的数据作答即可;
(2)观察纵轴统计图的数据,可知每格代表 5摄氏度。
(3)将每个季度的两地的平均气温作差,差最小的,那么这个季度两地平均气温最接近;差最大的,那么这个季度两地平均气温差距最大;
(4)把第四季度江门市平均气温比韶关市平均气温相减即可求得高了几度。
(5)将江门市全年平均气温加起来除以4即可解答。
【详解】(1)第一季度江门市平均气温是17摄氏度。
(2)上图中每格代表5摄氏度。
(3)第一季度:17-15=2(摄氏度)
第二季度:26-24=2(摄氏度)
第三季度:29-28=1(摄氏度)
第四季度:25-16=9(摄氏度)
两地平均气温最接近的是第三季度,平均气温差距最大的是第四季度。
(4)25-16=9(摄氏度)
第四季度江门市平均气温比韶关市平均气温高了9摄氏度。
(5)(17+26+28+25)÷4
=96÷4
=24(摄氏度)
答:江门市全年平均每月气温是24摄氏度。
23.19万人次
【分析】根据表格先求和算出5天的总客运量,再根据总数÷份数=每份数,即可求出。
【详解】(15.3+16.4+19.6+24.6+19.1)÷5
=(31.7+19.6+24.6+19.1)÷5
=(51.3+24.6+19.1)÷5
=(75.9+19.1)÷5
=95÷5
=19(万人次)
答:洛阳地铁1号线五一期间平均每天客运量19万人次。
答案第1页,共2页
答案第1页,共2页
