人教版小学数学四下三角形作业(带答案)
文档属性
| 名称 | 人教版小学数学四下三角形作业(带答案) |  | |
| 格式 | docx | ||
| 文件大小 | 573.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 07:58:50 | ||
图片预览


文档简介
小学数学四下三角形作业
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.在梯形里画一条线段,不可能把梯形分割成( )。
A.两个三角形 B.两个平行四边形 C.一个平行四边形和一个三角形
2.一个三角形的两条边分别是4厘米和7厘米,它的第三条边可能是( )厘米。
A.10 B.11 C.12
3.下列关于等腰三角形的说法,正确的有( )。
①等腰三角形一定是轴对称图形;
②有一个角是的等腰三角形不一定是等边三角形;
③等腰三角形的两个底角一定是锐角;
④有两条边相等的图形是等腰三角形。
A.①②③④ B.①③ C.②③ D.①④
4.四边形的内角和是三角形内角和的( )倍。
A.1 B.2 C.3
5.用4根木条钉成一个长方形,然后向相反的方向拉它的一组对角,就变成了一个平行四边形。这个平行四边形的内角和与原来长方形的内角和相比,( )。
A.相等 B.变大 C.变小
二、填空题
6.一个三角形的两个内角分别是37°和42°,另外一个内角是( )°,这是一个( )三角形。
7.数学课上,奇思画了一个三角形,有一个直角,有两条边相等,这是一个 三角形;妙想画了一个四边形,只有一组对边平行,没有直角,这是一个 形。
8.分一分。
(1)直角三角形的是( )。
(2)锐角三角形的是( )。
(3)钝角三角形的是( )。
(4)等腰三角形的是( )。
(5)等边三角形的是( )。
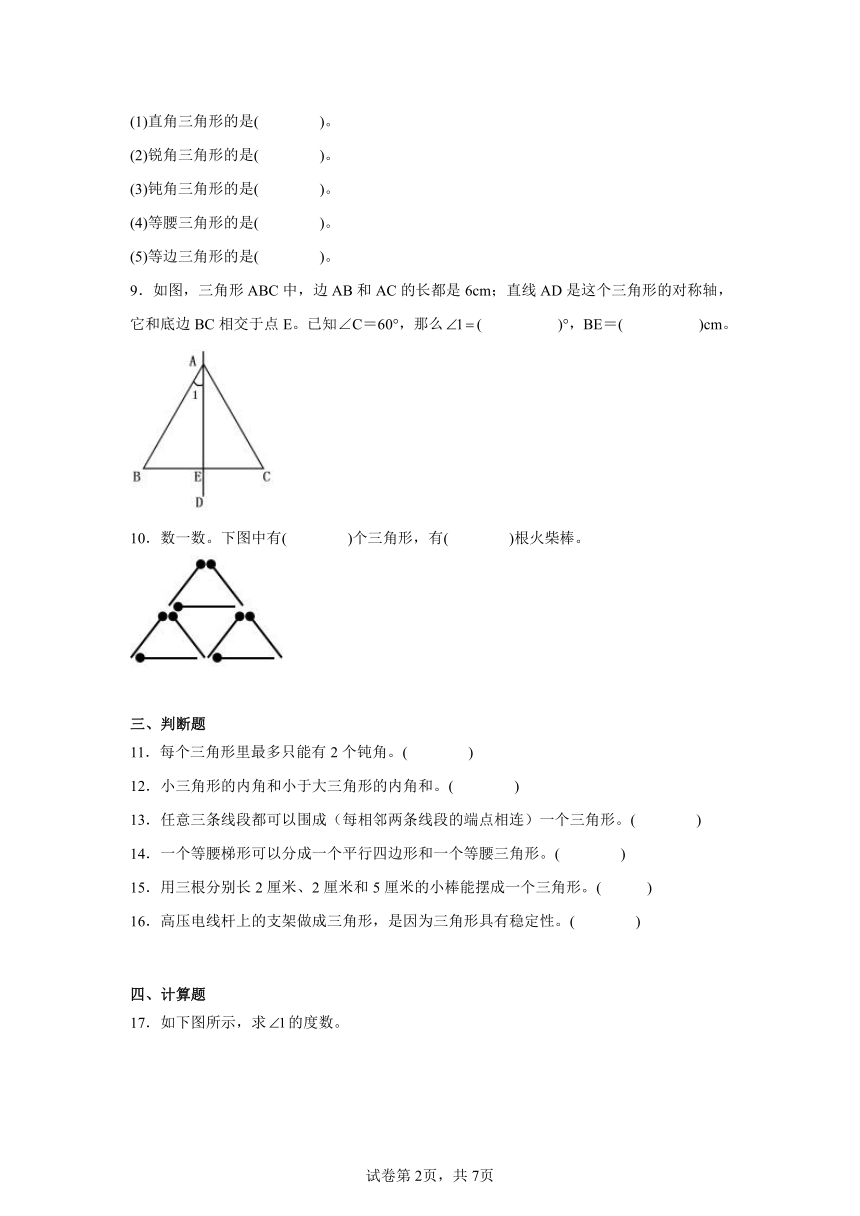
9.如图,三角形ABC中,边AB和AC的长都是6cm;直线AD是这个三角形的对称轴,它和底边BC相交于点E。已知∠C=60°,那么( )°,BE=( )cm。
10.数一数。下图中有( )个三角形,有( )根火柴棒。
三、判断题
11.每个三角形里最多只能有2个钝角。( )
12.小三角形的内角和小于大三角形的内角和。( )
13.任意三条线段都可以围成(每相邻两条线段的端点相连)一个三角形。( )
14.一个等腰梯形可以分成一个平行四边形和一个等腰三角形。( )
15.用三根分别长2厘米、2厘米和5厘米的小棒能摆成一个三角形。( )
16.高压电线杆上的支架做成三角形,是因为三角形具有稳定性。( )
四、计算题
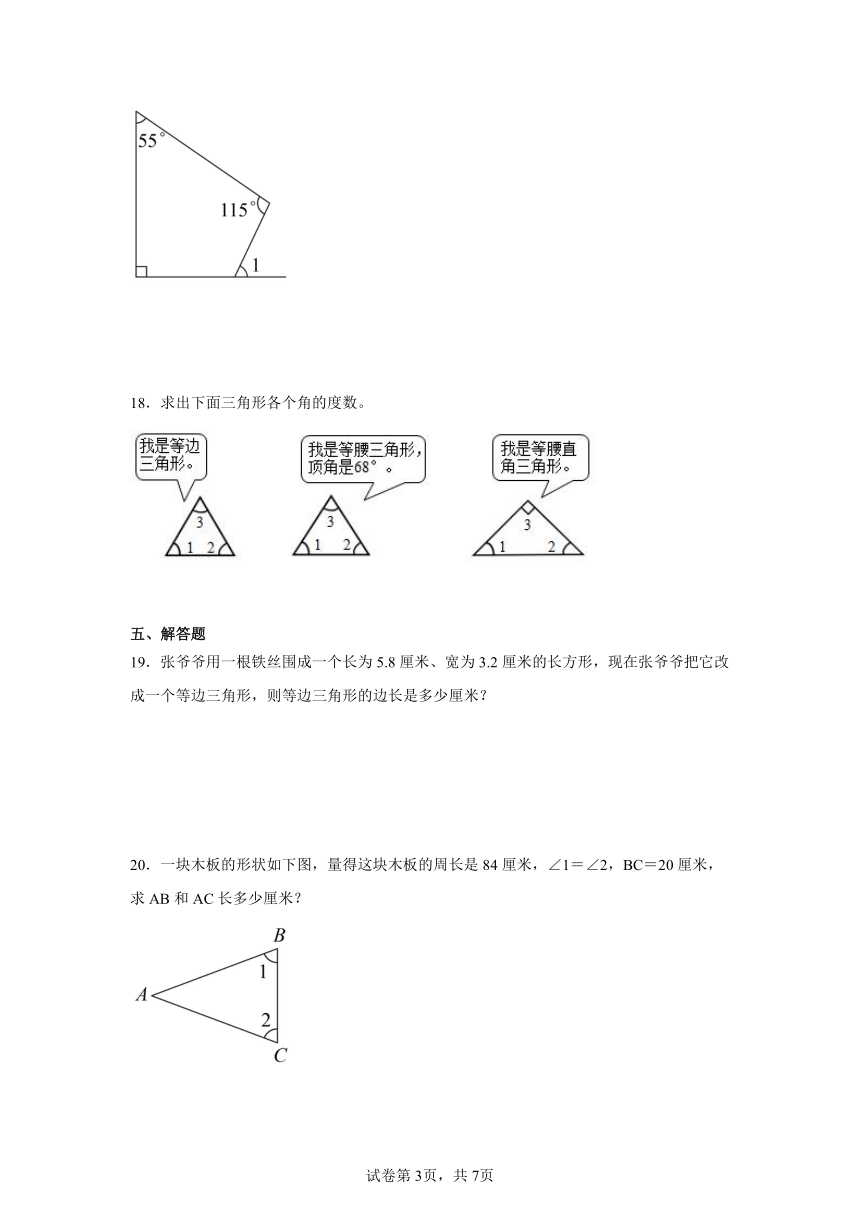
17.如下图所示,求的度数。
18.求出下面三角形各个角的度数。
五、解答题
19.张爷爷用一根铁丝围成一个长为5.8厘米、宽为3.2厘米的长方形,现在张爷爷把它改成一个等边三角形,则等边三角形的边长是多少厘米?
20.一块木板的形状如下图,量得这块木板的周长是84厘米,∠1=∠2,BC=20厘米,求AB和AC长多少厘米?
21.资料卡:
张凡的小练笔灯塔指引航船的方向
在这个充满了未知和危险的世界里,灯塔和小船是相互依存的。有了灯塔,小船才能顺利地航行在海上;有了小船,灯塔才有了存在的意义。正是因为有了这样的相互依存,才有了这个美丽而又神秘的海洋世界。
如下图,灯塔是海上的明灯,小船则是海上的勇士。灯塔A与灯塔B在同一直线上,轮船航行的轨迹与灯塔所在直线平行。
请根据以上材料中的信息解答下列各题。
考点1:三角形的特征
(1)当轮船航行至C点处,如果依次连结A、B、C三点,轮船与两座灯塔形成的是( )形。
(2)一个三角形有( )个( ),( )个( ),( )条( )。
(3)从三角形的( )向( )作一条( ),( )和( )之间的距离叫做三角形的( ),这条对边叫做三角形的( )。一个三角形最多可以画( )条高。
(4)画出图形ABC的每条边上的高。
考点2:三边关系
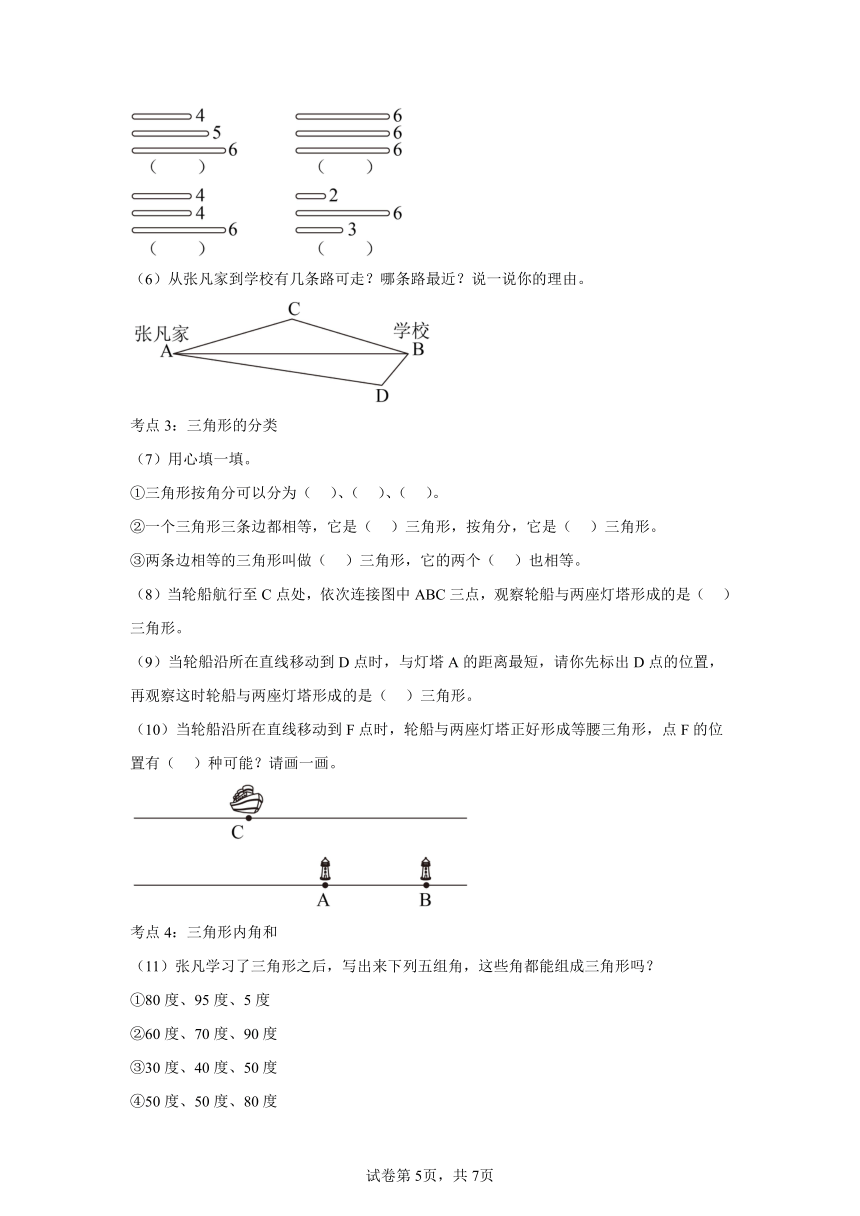
(5)五年级的张凡同学想制作一个轮船与两座灯塔形成的图形模型,他准备了一些小棒,请在能围成的各组小棒下面画“√”。(单位:厘米)
(6)从张凡家到学校有几条路可走?哪条路最近?说一说你的理由。
考点3:三角形的分类
(7)用心填一填。
①三角形按角分可以分为( )、( )、( )。
②一个三角形三条边都相等,它是( )三角形,按角分,它是( )三角形。
③两条边相等的三角形叫做( )三角形,它的两个( )也相等。
(8)当轮船航行至C点处,依次连接图中ABC三点,观察轮船与两座灯塔形成的是( )三角形。
(9)当轮船沿所在直线移动到D点时,与灯塔A的距离最短,请你先标出D点的位置,再观察这时轮船与两座灯塔形成的是( )三角形。
(10)当轮船沿所在直线移动到F点时,轮船与两座灯塔正好形成等腰三角形,点F的位置有( )种可能?请画一画。
考点4:三角形内角和
(11)张凡学习了三角形之后,写出来下列五组角,这些角都能组成三角形吗?
①80度、95度、5度
②60度、70度、90度
③30度、40度、50度
④50度、50度、80度
⑤60度、60度、60度
我认为有( )组角可以组成三角形,它们分别为( )(填序号),我的理由是( )。
考点5:四边形内角和
(12)这是张凡探究多边形内角和的学习单,你能帮他接着往下探究吗?请你画一画、算一算,把下列表格填写完整并写出你的发现。
图形名称 边数 图形 分成的三角个数 内角和
三角形 3 1 180度
四边形 4 2 360度
五边形 5
六边形 6
七边形 7
……
我发现:______________________________________________________________。
22.按要求做题。
(1)画出上图三角形指定边上的高。
(2)如果在上图三角形ABC中,∠B=120°,∠A=20°,那么∠C=( )°。
(3)在计算∠C的度数时,你利用了三角形的内角和等于( )°。
如果让你验证“三角形的内角和等于180°”,你会用什么方法?请简要描述。
____________________________________________________________________________。
23.多边形内角和的探究实践。
下面左图是大理民居中的六边形窗户。看着这幅窗户图,小明回想起了“多边形的内角和”问题:
这是他探索几种多边形内角和的研究过程记录表:
多边形 ……
多边形的边数 5 6 7 8 …
分割 结果 三角形个数 1 0 1 0 …
四边形个数 1 2 2 3 …
①请你接着把记录表补充完整。
②照这样的方法分割下去,十二边形中最多能分割成( )个四边形来计算内角和。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】梯形只有一组对边平行,平行四边形两组对边分别平行。在梯形里面画一条线段,不能做到分割后的两个图形都有两组分别平行的对边;据此解答。
【详解】
A.在梯形里画一条线段,可能把梯形分割成两个三角形,
B.在梯形里画一条线段,不可能把梯形分割成两个平行四边形。
C.在梯形里画一条线段,可能把梯形分割成一个平行四边形和一个三角形,。
故答案为:B
2.A
【分析】根据三角形任意两条边长度之和大于第三条边,可以计算出已知两条边的和与差,确定第三条边的范围,即可解答。
【详解】4+7=11(厘米)
7-4=3(厘米)
所以,第三条边的长度应该大于3厘米小于11厘米。它的第三条边可能是10厘米。
故答案为:A
3.B
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;等腰三角形的两腰相等、两个底角也相等;小于90°的角锐角,三角形的内角和为180°,依此判断。
【详解】
①等腰三角形一定是轴对称图形,如图所示:,即原说法正确。
②当60°为顶角时,则底角为:180°-60°=120°,120°÷2=60°;当60°为底角时,顶角为:180°-60°-60°=60°,因此有一个角是的等腰三角形一定是等边三角形,即原说法错误。
③假设等腰三角形的两个底角都是直角或钝角,90°+90°=180°,100°+100°=200°>180°,因此等腰三角形的两个底角一定是锐角,即原说法正确。
④三角形是由三条边组成,因此有两条边相等的三角形是等腰三角形,即原说法错误。
因此正确的有:①③。
故答案为:B
4.B
【分析】
三角形的内角和是180°,四边形的内角和是360°,2个180°是360°,由此可知是2倍的关系。
【详解】360°÷180°=2,四边形的内角和是三角形内角和的2倍。
故答案为:B
5.A
【分析】
长方形是四边形,平行四边形也是四边形,四边形内角和是360°,所以将一个长方形拉成平行四边形,内角和不会发生变化。
【详解】这个平行四边形的内角和与原来长方形的内角和相比,内角和相等,还是360°。
故答案为:A
6. 101 钝角
【分析】三角形内角和180°,用180°依次减去已知的两个内角的度数就是第3个内角的度数。再根据三个角的度数确定这是个什么类型的三角形。
三角形按角的大小,可分为三种:三个角都是锐角的三角形,叫锐角三角形;有一个角是直角的三角形,叫直角三角形;有一个角是钝角的三角形,叫钝角三角形。
【详解】180°-37°-42°
=143°-42°
=101°
一个三角形的两个内角分别是37°和42°,另外一个内角是(101)°,这是一个(钝角)三角形。
7. 等腰直角 梯
【分析】三角形按边分类:有两条边相等的三角形是等腰三角形,有三条边相等的是等边三角形;只有一组对边平行的四边形叫作梯形;据此解答。
【详解】奇思画了一个三角形,有一个直角,有两条边相等,这是一个等腰直角三角形;妙想画了一个四边形,只有一组对边平行,没有直角,这是一个梯形。
8.(1)①⑥
(2)②④
(3)③⑤
(4)②⑤
(5)④
【分析】有一个角是直角的三角形是直角三角形,直角=90°;有一个钝角的三角形是钝角三角形,钝角是大于90°且小于180°的角;三个角都是锐角的三角形是锐角三角形,锐角是小于90°的角;等腰三角形的两条边相等;等边三角形的三条边相等,据此选择即可。
【详解】(1)根据分析可知,直角三角形的是①⑥。
(2)根据分析可知,锐角三角形的是②④。
(3)根据分析可知,钝角三角形的是③⑤。
(4)根据分析可知,等腰三角形的是②⑤。
(5)根据分析可知,等边三角形的是④。
9. 30 3
【分析】根据题中的已知条件,两条边相等和其中一个角是60°推断出这个三角形是等边三角形,再利用对称的知识求出的度数和线段BE的长度。
【详解】因为边AB和AC的长都是6cm,所以三角形ABC是等腰三角形,又因为∠C=60°,所以∠B=60°(等腰三角形的两底角相等);因为三角形内角和180°,所以∠BAC=180°-∠C-∠B=180°-60°-60°=120°-60°=60°,所以三角形ABC是等边三角形。
因为直线AD是这个三角形的对称轴,所以直线AD平分∠BAC,平分线段BC。
所以,BE=6÷2=3厘米。
【点睛】熟练掌握等边三角形的判定和性质,是解答此题的关键。
10. 5 9
【分析】(1)观察图形可知,小的三角形有4个,整体是也是1个大三角形,4+1=5(个),据此解答;
(2)根据数数的方法数出火柴棒的数量即可。
【详解】(1)4+1=5个,所以图中有5个三角形;
(2)图中有9根火柴棒。
【点睛】本题考查了组合图形中三角形的计数,此类问题,要分类进行计数,避免重复或遗漏。
11.×
【分析】三角形的内角和是180度,钝角大于90度小于180度,所以一个三角形中最多只有一个钝角,依此解答即可。
【详解】根据分析可知,每个三角形里最多只能有2个钝角,此说法错误。
故答案为:×
12.×
【分析】三角形的内角和是180°,据此判断。
【详解】三角形无论大小,内角和都是180°,因此,原题说法错误。
故答案为:×
13.×
【分析】三条线段要想围成三角形,就得满足:三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【详解】据分析可知:只有满足任意两条线段的和大于第三条线段的三条线段才能构成三角形。
故答案为:×
14.√
【分析】如下图,把一个等腰梯形分成了一平行四边形和一个等腰三角形,据此即可解答。
【详解】根据分析可知,一个等腰梯形可以分成一个平行四边形和一个等腰三角形,原说法正确。
故答案为:√
15.×
【分析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边;解答验证即可。
【详解】2+2<5,所以长2厘米、2厘米和5厘米的三根小棒不能摆成一个三角形。说法错误。
故答案为:×
16.√
【分析】三角形具有稳定性的特征,生活中常常利用三角形这一特性对物体进行稳固,据此判断。
【详解】三角形具有稳定性,所以题目说法正确。
故答案为:√
【点睛】解决本题的关键是正确理解三角形的稳定性特征。
17.80°
【分析】四边形的内角和为360°。图中四边形一共有四个角,有1个直角,直角的度数为90°。可以先算出给出的三个角的度数之和,再用360°减去这三个角的度数之和即可得到剩下的那个角的度数,再用180°减去这个角度,就求出了∠1的度数。
【详解】90°+55°+115°=260°
360°-260°=100°
180°-100°=80°
∠1的度数是80°
18.(1)∠1=60°、∠2=60°、∠3=60°
(2)∠1=56°、∠2=56°、∠3=68°
(3)∠1=45°、∠2=45°、∠3=90°
【分析】(1)等边三角形:三条边都相等且三个内角均相等,都是60°。
(2)等腰三角形:有两条边相等的三角形,在等腰三角形中,相等的两条边叫做腰,另一条边叫做底;两腰的夹角叫做顶角,底边上的两个角叫做底角;等腰三角形的两个底角相等。
(3)有一个角是直角的三角形是直角三角形。
【详解】(1)180°÷3=60°
则∠1=60°、∠2=60°、∠3=60°。
(2)(180°-68°)÷2
=112°÷2
=56°
则∠1=56°、∠2=56°、∠3=68°。
(3)(180°-90°)÷2
=90°÷2
=45°
则∠1=45°、∠2=45°、∠3=90°。
19.6厘米
【分析】先根据长方形周长=(长+宽)×2求出铁丝的长度,等边三角形的边长相等,所以再用铁丝的长度除以3即可求出等边三角形的边长。
【详解】(5.8+3.2)×2
=9×2
=18(厘米)
18÷3=6(厘米)
答:等边三角形的边长是6厘米
20.32厘米
【分析】因为∠1=∠2,所以这是一个等腰三角形,三角形的周长和底边已知,因为等腰三角形的两条腰相等,所以利用三角形的周长减去底边长然后除以2,即可解答。
【详解】因为∠1=∠2,所以三角形为等腰三角形,
AB=AC
(84-20)÷2
=64÷2
=32(厘米)
答:AB和AC长32厘米。
21.(1)三角
(2)3;顶点;3;角;3;边
(3)任一顶点;对边或对边的延长线;垂线;顶点;垂足;高;底;3
(4)画图见详解
(5)打勾见详解
(6)3条;A→B最短;两点之间线段最短;
(7)①锐角三角形;直角三角形;钝角三角形
②等边;锐角;
③等腰;底角
(8)钝角
(9)D点位置见详解;直角;
(10)3;画一画见详解;
(11)3;①④⑤;三角形内角和为180度
(12)画一画,算一算填表见详解;多边形内角和为:(边数-2)乘180度,边数大于等于3
【分析】(1)根据由同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形是三角形由此可知,连接A、B、C三点,组成的是三角形;据此可解此题
(2)一个三角形有3个顶点,3个角,3条边;据此可解此题
(3)考查三角形高的画法,从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高。这个顶点所对的边叫做三角形的底。一个三角形最多有3条高;据此可解此题。
(4)根据(3)中高的画法,进行画高即可。
(5)根据三角形两边之和大于第三边,4+5=9>6,可以围成三级形;6+6=12>6,可以围成三级形;4+4=8>6,可以围成三级形;2+3=5<6,不可以围成三级形;据此进行打勾判断。
(6)从张凡家到学校可以是A→C→B;A→B或者A→D→B;有3种方法;最短的距离是A→B;因为两点之间直线最短;据此可解此题。
(7)三角形按角分可以分为锐角三角形、直角三角形、钝角三角形。一个三角形三条边都相等,它是等边三角形,按角分,它是锐角三角形。两条边相等的三角形叫做等腰三角形,它的两个底角也相等;据此可解此题。
(8)根据三角形中有一个角大于90度的三角形是钝角三角形,据此可解此题。
(9)根据两条平行线之间垂线段最短,据此可画出D点位置,然后根据有一个角为90度的三角形为直角三角形,据此可解此题。
(10)等腰三角形的两条腰可以是AF=BF,或者AB=AF亦或者AB=BF,所以有三种情况,分别按照上述三种情况进行作图即可解此题。
(11)三角形的内角和为180度,据此进行判断:
①80度、95度、5度:80+95+5=180,符合。
②60度、70度、90度:60+70+90=220,不符合。
③30度、40度、50度:30+40+50=120,不符合。
④50度、50度、80度:50+50+80=180,符合。
⑤60度、60度、60度:60+60+60=180,符合。据此可解此题。
(12)将多边形分割成三角形,然后据此数出三角形的个数,以及计算出多边形的内角和;据此可发现规律多边形的内角和为:(边数-2)乘180度,边数大于等于3;据此可解此题。
【详解】根据分析
(1)当轮船航行至C点处,如果依次连结A、B、C三点,轮船与两座灯塔形成的是三角形。
(2)一个三角形有3个顶点,3个角,3条边。
(3)从三角形的任一顶点向对边或对边的延长线作一条垂线,顶点和垂足之间的距离叫做三角形的高,这条对边叫做三角形的底。一个三角形最多可以画3条高。
(4)画一画如图:
(5)如下图:
(6)根据分析,从张凡家到学校有三种方法分别是:
①A→C→B;
②A→B;
③A→D→B;
最短的距离是A→B;因为两点之间直线最短。
(7)①三角形按角分可以分为锐角三角形、直角三角形、钝角三角形。
②一个三角形三条边都相等,它是等边三角形,按角分,它是锐角三角形。
③两条边相等的三角形叫做等腰三角形,它的两个底角也相等。
(8)当轮船航行至C点处,依次连接图中ABC三点,观察轮船与两座灯塔形成的是钝角三角形。
(9)D点的位置如下图:
这时轮船与两座灯塔形成的是直角三角形。
(10)当轮船沿所在直线移动到F点时,轮船与两座灯塔正好形成等腰三角形,点F的位置有3种可能;画一画如下:
(11)由分析可知,我认为有3组角可以组成三角形,它们分别为①④⑤,我的理由是三角形的内角和为180度。
(12)五边形内角和:(5-2)×180=540(度)
六边形内角和:(6-2)×180=720(度)
七边形内角和:(7-2)×180=900(度)
填表如下:
图形名称 边数 图形 分成的三角个数 内角和
三角形 3 1 180度
四边形 4 2 360度
五边形 5 3 540度
六边形 6 4 720度
七边形 7 5 900度
……
我发现:多边形内角和为:(边数-2)乘180度,边数大于等于3。
22.(1)见详解;
(2)40;
(3)180;见详解
【分析】(1)作线段CB的延长线,从A点向CB的延长线作垂线,标记为点D, AD即为三角形ABC底边上的高,据此作答;
(2)根据三角形的内角和=180°,在三角形ABC中,∠B=120°,∠A=20°,那么∠C=180°-120°-20°,据此作答。
(3)验证三角形的内角和等于180°,可以用拼接法,先把三角形的三个角剪下来,再拼一拼,看看是否能拼成一个平角,据此作答。
【详解】(1)作图如下:
(2)180°-120°-20°
=60°-20°
=40°
所以∠C=40°。
(3)理由如下:
如图,拼接成了一个平角,所以可以证明三角形的内角和是180°。
23.①见详解
②5
【分析】①根据图数出多边形的边数以及分割成的三角形个数和四边形的个数即可;
②由于一个四边形可以分割成两个三角形,多边形的边数是5的时候,相当于可以分割3个三角形;六边形相当于可以分割4个三角形;七边形相当于可以分割5个三角形,由此即可知道多边形的变数减去2即可求出分割的三角形个数,再除以2即可求出分割的四边形的个数,据此即可求解。
【详解】由分析可知:①
多边形 ……
多边形的边数 5 6 7 8 9 10 …
分割 结果 三角形个数 1 0 1 0 1 0 …
四边形个数 1 2 2 3 3 4 …
②12-2=10
10÷2=5(个)
所以十二边形中最多能分割成5个四边形来计算内角和。
【点睛】本题主要考查平面图形的分割,同时要清楚四边形和三角形的关系是解题的关键。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.在梯形里画一条线段,不可能把梯形分割成( )。
A.两个三角形 B.两个平行四边形 C.一个平行四边形和一个三角形
2.一个三角形的两条边分别是4厘米和7厘米,它的第三条边可能是( )厘米。
A.10 B.11 C.12
3.下列关于等腰三角形的说法,正确的有( )。
①等腰三角形一定是轴对称图形;
②有一个角是的等腰三角形不一定是等边三角形;
③等腰三角形的两个底角一定是锐角;
④有两条边相等的图形是等腰三角形。
A.①②③④ B.①③ C.②③ D.①④
4.四边形的内角和是三角形内角和的( )倍。
A.1 B.2 C.3
5.用4根木条钉成一个长方形,然后向相反的方向拉它的一组对角,就变成了一个平行四边形。这个平行四边形的内角和与原来长方形的内角和相比,( )。
A.相等 B.变大 C.变小
二、填空题
6.一个三角形的两个内角分别是37°和42°,另外一个内角是( )°,这是一个( )三角形。
7.数学课上,奇思画了一个三角形,有一个直角,有两条边相等,这是一个 三角形;妙想画了一个四边形,只有一组对边平行,没有直角,这是一个 形。
8.分一分。
(1)直角三角形的是( )。
(2)锐角三角形的是( )。
(3)钝角三角形的是( )。
(4)等腰三角形的是( )。
(5)等边三角形的是( )。
9.如图,三角形ABC中,边AB和AC的长都是6cm;直线AD是这个三角形的对称轴,它和底边BC相交于点E。已知∠C=60°,那么( )°,BE=( )cm。
10.数一数。下图中有( )个三角形,有( )根火柴棒。
三、判断题
11.每个三角形里最多只能有2个钝角。( )
12.小三角形的内角和小于大三角形的内角和。( )
13.任意三条线段都可以围成(每相邻两条线段的端点相连)一个三角形。( )
14.一个等腰梯形可以分成一个平行四边形和一个等腰三角形。( )
15.用三根分别长2厘米、2厘米和5厘米的小棒能摆成一个三角形。( )
16.高压电线杆上的支架做成三角形,是因为三角形具有稳定性。( )
四、计算题
17.如下图所示,求的度数。
18.求出下面三角形各个角的度数。
五、解答题
19.张爷爷用一根铁丝围成一个长为5.8厘米、宽为3.2厘米的长方形,现在张爷爷把它改成一个等边三角形,则等边三角形的边长是多少厘米?
20.一块木板的形状如下图,量得这块木板的周长是84厘米,∠1=∠2,BC=20厘米,求AB和AC长多少厘米?
21.资料卡:
张凡的小练笔灯塔指引航船的方向
在这个充满了未知和危险的世界里,灯塔和小船是相互依存的。有了灯塔,小船才能顺利地航行在海上;有了小船,灯塔才有了存在的意义。正是因为有了这样的相互依存,才有了这个美丽而又神秘的海洋世界。
如下图,灯塔是海上的明灯,小船则是海上的勇士。灯塔A与灯塔B在同一直线上,轮船航行的轨迹与灯塔所在直线平行。
请根据以上材料中的信息解答下列各题。
考点1:三角形的特征
(1)当轮船航行至C点处,如果依次连结A、B、C三点,轮船与两座灯塔形成的是( )形。
(2)一个三角形有( )个( ),( )个( ),( )条( )。
(3)从三角形的( )向( )作一条( ),( )和( )之间的距离叫做三角形的( ),这条对边叫做三角形的( )。一个三角形最多可以画( )条高。
(4)画出图形ABC的每条边上的高。
考点2:三边关系
(5)五年级的张凡同学想制作一个轮船与两座灯塔形成的图形模型,他准备了一些小棒,请在能围成的各组小棒下面画“√”。(单位:厘米)
(6)从张凡家到学校有几条路可走?哪条路最近?说一说你的理由。
考点3:三角形的分类
(7)用心填一填。
①三角形按角分可以分为( )、( )、( )。
②一个三角形三条边都相等,它是( )三角形,按角分,它是( )三角形。
③两条边相等的三角形叫做( )三角形,它的两个( )也相等。
(8)当轮船航行至C点处,依次连接图中ABC三点,观察轮船与两座灯塔形成的是( )三角形。
(9)当轮船沿所在直线移动到D点时,与灯塔A的距离最短,请你先标出D点的位置,再观察这时轮船与两座灯塔形成的是( )三角形。
(10)当轮船沿所在直线移动到F点时,轮船与两座灯塔正好形成等腰三角形,点F的位置有( )种可能?请画一画。
考点4:三角形内角和
(11)张凡学习了三角形之后,写出来下列五组角,这些角都能组成三角形吗?
①80度、95度、5度
②60度、70度、90度
③30度、40度、50度
④50度、50度、80度
⑤60度、60度、60度
我认为有( )组角可以组成三角形,它们分别为( )(填序号),我的理由是( )。
考点5:四边形内角和
(12)这是张凡探究多边形内角和的学习单,你能帮他接着往下探究吗?请你画一画、算一算,把下列表格填写完整并写出你的发现。
图形名称 边数 图形 分成的三角个数 内角和
三角形 3 1 180度
四边形 4 2 360度
五边形 5
六边形 6
七边形 7
……
我发现:______________________________________________________________。
22.按要求做题。
(1)画出上图三角形指定边上的高。
(2)如果在上图三角形ABC中,∠B=120°,∠A=20°,那么∠C=( )°。
(3)在计算∠C的度数时,你利用了三角形的内角和等于( )°。
如果让你验证“三角形的内角和等于180°”,你会用什么方法?请简要描述。
____________________________________________________________________________。
23.多边形内角和的探究实践。
下面左图是大理民居中的六边形窗户。看着这幅窗户图,小明回想起了“多边形的内角和”问题:
这是他探索几种多边形内角和的研究过程记录表:
多边形 ……
多边形的边数 5 6 7 8 …
分割 结果 三角形个数 1 0 1 0 …
四边形个数 1 2 2 3 …
①请你接着把记录表补充完整。
②照这样的方法分割下去,十二边形中最多能分割成( )个四边形来计算内角和。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】梯形只有一组对边平行,平行四边形两组对边分别平行。在梯形里面画一条线段,不能做到分割后的两个图形都有两组分别平行的对边;据此解答。
【详解】
A.在梯形里画一条线段,可能把梯形分割成两个三角形,
B.在梯形里画一条线段,不可能把梯形分割成两个平行四边形。
C.在梯形里画一条线段,可能把梯形分割成一个平行四边形和一个三角形,。
故答案为:B
2.A
【分析】根据三角形任意两条边长度之和大于第三条边,可以计算出已知两条边的和与差,确定第三条边的范围,即可解答。
【详解】4+7=11(厘米)
7-4=3(厘米)
所以,第三条边的长度应该大于3厘米小于11厘米。它的第三条边可能是10厘米。
故答案为:A
3.B
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;等腰三角形的两腰相等、两个底角也相等;小于90°的角锐角,三角形的内角和为180°,依此判断。
【详解】
①等腰三角形一定是轴对称图形,如图所示:,即原说法正确。
②当60°为顶角时,则底角为:180°-60°=120°,120°÷2=60°;当60°为底角时,顶角为:180°-60°-60°=60°,因此有一个角是的等腰三角形一定是等边三角形,即原说法错误。
③假设等腰三角形的两个底角都是直角或钝角,90°+90°=180°,100°+100°=200°>180°,因此等腰三角形的两个底角一定是锐角,即原说法正确。
④三角形是由三条边组成,因此有两条边相等的三角形是等腰三角形,即原说法错误。
因此正确的有:①③。
故答案为:B
4.B
【分析】
三角形的内角和是180°,四边形的内角和是360°,2个180°是360°,由此可知是2倍的关系。
【详解】360°÷180°=2,四边形的内角和是三角形内角和的2倍。
故答案为:B
5.A
【分析】
长方形是四边形,平行四边形也是四边形,四边形内角和是360°,所以将一个长方形拉成平行四边形,内角和不会发生变化。
【详解】这个平行四边形的内角和与原来长方形的内角和相比,内角和相等,还是360°。
故答案为:A
6. 101 钝角
【分析】三角形内角和180°,用180°依次减去已知的两个内角的度数就是第3个内角的度数。再根据三个角的度数确定这是个什么类型的三角形。
三角形按角的大小,可分为三种:三个角都是锐角的三角形,叫锐角三角形;有一个角是直角的三角形,叫直角三角形;有一个角是钝角的三角形,叫钝角三角形。
【详解】180°-37°-42°
=143°-42°
=101°
一个三角形的两个内角分别是37°和42°,另外一个内角是(101)°,这是一个(钝角)三角形。
7. 等腰直角 梯
【分析】三角形按边分类:有两条边相等的三角形是等腰三角形,有三条边相等的是等边三角形;只有一组对边平行的四边形叫作梯形;据此解答。
【详解】奇思画了一个三角形,有一个直角,有两条边相等,这是一个等腰直角三角形;妙想画了一个四边形,只有一组对边平行,没有直角,这是一个梯形。
8.(1)①⑥
(2)②④
(3)③⑤
(4)②⑤
(5)④
【分析】有一个角是直角的三角形是直角三角形,直角=90°;有一个钝角的三角形是钝角三角形,钝角是大于90°且小于180°的角;三个角都是锐角的三角形是锐角三角形,锐角是小于90°的角;等腰三角形的两条边相等;等边三角形的三条边相等,据此选择即可。
【详解】(1)根据分析可知,直角三角形的是①⑥。
(2)根据分析可知,锐角三角形的是②④。
(3)根据分析可知,钝角三角形的是③⑤。
(4)根据分析可知,等腰三角形的是②⑤。
(5)根据分析可知,等边三角形的是④。
9. 30 3
【分析】根据题中的已知条件,两条边相等和其中一个角是60°推断出这个三角形是等边三角形,再利用对称的知识求出的度数和线段BE的长度。
【详解】因为边AB和AC的长都是6cm,所以三角形ABC是等腰三角形,又因为∠C=60°,所以∠B=60°(等腰三角形的两底角相等);因为三角形内角和180°,所以∠BAC=180°-∠C-∠B=180°-60°-60°=120°-60°=60°,所以三角形ABC是等边三角形。
因为直线AD是这个三角形的对称轴,所以直线AD平分∠BAC,平分线段BC。
所以,BE=6÷2=3厘米。
【点睛】熟练掌握等边三角形的判定和性质,是解答此题的关键。
10. 5 9
【分析】(1)观察图形可知,小的三角形有4个,整体是也是1个大三角形,4+1=5(个),据此解答;
(2)根据数数的方法数出火柴棒的数量即可。
【详解】(1)4+1=5个,所以图中有5个三角形;
(2)图中有9根火柴棒。
【点睛】本题考查了组合图形中三角形的计数,此类问题,要分类进行计数,避免重复或遗漏。
11.×
【分析】三角形的内角和是180度,钝角大于90度小于180度,所以一个三角形中最多只有一个钝角,依此解答即可。
【详解】根据分析可知,每个三角形里最多只能有2个钝角,此说法错误。
故答案为:×
12.×
【分析】三角形的内角和是180°,据此判断。
【详解】三角形无论大小,内角和都是180°,因此,原题说法错误。
故答案为:×
13.×
【分析】三条线段要想围成三角形,就得满足:三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【详解】据分析可知:只有满足任意两条线段的和大于第三条线段的三条线段才能构成三角形。
故答案为:×
14.√
【分析】如下图,把一个等腰梯形分成了一平行四边形和一个等腰三角形,据此即可解答。
【详解】根据分析可知,一个等腰梯形可以分成一个平行四边形和一个等腰三角形,原说法正确。
故答案为:√
15.×
【分析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边;解答验证即可。
【详解】2+2<5,所以长2厘米、2厘米和5厘米的三根小棒不能摆成一个三角形。说法错误。
故答案为:×
16.√
【分析】三角形具有稳定性的特征,生活中常常利用三角形这一特性对物体进行稳固,据此判断。
【详解】三角形具有稳定性,所以题目说法正确。
故答案为:√
【点睛】解决本题的关键是正确理解三角形的稳定性特征。
17.80°
【分析】四边形的内角和为360°。图中四边形一共有四个角,有1个直角,直角的度数为90°。可以先算出给出的三个角的度数之和,再用360°减去这三个角的度数之和即可得到剩下的那个角的度数,再用180°减去这个角度,就求出了∠1的度数。
【详解】90°+55°+115°=260°
360°-260°=100°
180°-100°=80°
∠1的度数是80°
18.(1)∠1=60°、∠2=60°、∠3=60°
(2)∠1=56°、∠2=56°、∠3=68°
(3)∠1=45°、∠2=45°、∠3=90°
【分析】(1)等边三角形:三条边都相等且三个内角均相等,都是60°。
(2)等腰三角形:有两条边相等的三角形,在等腰三角形中,相等的两条边叫做腰,另一条边叫做底;两腰的夹角叫做顶角,底边上的两个角叫做底角;等腰三角形的两个底角相等。
(3)有一个角是直角的三角形是直角三角形。
【详解】(1)180°÷3=60°
则∠1=60°、∠2=60°、∠3=60°。
(2)(180°-68°)÷2
=112°÷2
=56°
则∠1=56°、∠2=56°、∠3=68°。
(3)(180°-90°)÷2
=90°÷2
=45°
则∠1=45°、∠2=45°、∠3=90°。
19.6厘米
【分析】先根据长方形周长=(长+宽)×2求出铁丝的长度,等边三角形的边长相等,所以再用铁丝的长度除以3即可求出等边三角形的边长。
【详解】(5.8+3.2)×2
=9×2
=18(厘米)
18÷3=6(厘米)
答:等边三角形的边长是6厘米
20.32厘米
【分析】因为∠1=∠2,所以这是一个等腰三角形,三角形的周长和底边已知,因为等腰三角形的两条腰相等,所以利用三角形的周长减去底边长然后除以2,即可解答。
【详解】因为∠1=∠2,所以三角形为等腰三角形,
AB=AC
(84-20)÷2
=64÷2
=32(厘米)
答:AB和AC长32厘米。
21.(1)三角
(2)3;顶点;3;角;3;边
(3)任一顶点;对边或对边的延长线;垂线;顶点;垂足;高;底;3
(4)画图见详解
(5)打勾见详解
(6)3条;A→B最短;两点之间线段最短;
(7)①锐角三角形;直角三角形;钝角三角形
②等边;锐角;
③等腰;底角
(8)钝角
(9)D点位置见详解;直角;
(10)3;画一画见详解;
(11)3;①④⑤;三角形内角和为180度
(12)画一画,算一算填表见详解;多边形内角和为:(边数-2)乘180度,边数大于等于3
【分析】(1)根据由同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形是三角形由此可知,连接A、B、C三点,组成的是三角形;据此可解此题
(2)一个三角形有3个顶点,3个角,3条边;据此可解此题
(3)考查三角形高的画法,从三角形任一顶点向它的对边或者对边的延长线作垂线,从顶点到垂足间的线段叫做三角形的高。这个顶点所对的边叫做三角形的底。一个三角形最多有3条高;据此可解此题。
(4)根据(3)中高的画法,进行画高即可。
(5)根据三角形两边之和大于第三边,4+5=9>6,可以围成三级形;6+6=12>6,可以围成三级形;4+4=8>6,可以围成三级形;2+3=5<6,不可以围成三级形;据此进行打勾判断。
(6)从张凡家到学校可以是A→C→B;A→B或者A→D→B;有3种方法;最短的距离是A→B;因为两点之间直线最短;据此可解此题。
(7)三角形按角分可以分为锐角三角形、直角三角形、钝角三角形。一个三角形三条边都相等,它是等边三角形,按角分,它是锐角三角形。两条边相等的三角形叫做等腰三角形,它的两个底角也相等;据此可解此题。
(8)根据三角形中有一个角大于90度的三角形是钝角三角形,据此可解此题。
(9)根据两条平行线之间垂线段最短,据此可画出D点位置,然后根据有一个角为90度的三角形为直角三角形,据此可解此题。
(10)等腰三角形的两条腰可以是AF=BF,或者AB=AF亦或者AB=BF,所以有三种情况,分别按照上述三种情况进行作图即可解此题。
(11)三角形的内角和为180度,据此进行判断:
①80度、95度、5度:80+95+5=180,符合。
②60度、70度、90度:60+70+90=220,不符合。
③30度、40度、50度:30+40+50=120,不符合。
④50度、50度、80度:50+50+80=180,符合。
⑤60度、60度、60度:60+60+60=180,符合。据此可解此题。
(12)将多边形分割成三角形,然后据此数出三角形的个数,以及计算出多边形的内角和;据此可发现规律多边形的内角和为:(边数-2)乘180度,边数大于等于3;据此可解此题。
【详解】根据分析
(1)当轮船航行至C点处,如果依次连结A、B、C三点,轮船与两座灯塔形成的是三角形。
(2)一个三角形有3个顶点,3个角,3条边。
(3)从三角形的任一顶点向对边或对边的延长线作一条垂线,顶点和垂足之间的距离叫做三角形的高,这条对边叫做三角形的底。一个三角形最多可以画3条高。
(4)画一画如图:
(5)如下图:
(6)根据分析,从张凡家到学校有三种方法分别是:
①A→C→B;
②A→B;
③A→D→B;
最短的距离是A→B;因为两点之间直线最短。
(7)①三角形按角分可以分为锐角三角形、直角三角形、钝角三角形。
②一个三角形三条边都相等,它是等边三角形,按角分,它是锐角三角形。
③两条边相等的三角形叫做等腰三角形,它的两个底角也相等。
(8)当轮船航行至C点处,依次连接图中ABC三点,观察轮船与两座灯塔形成的是钝角三角形。
(9)D点的位置如下图:
这时轮船与两座灯塔形成的是直角三角形。
(10)当轮船沿所在直线移动到F点时,轮船与两座灯塔正好形成等腰三角形,点F的位置有3种可能;画一画如下:
(11)由分析可知,我认为有3组角可以组成三角形,它们分别为①④⑤,我的理由是三角形的内角和为180度。
(12)五边形内角和:(5-2)×180=540(度)
六边形内角和:(6-2)×180=720(度)
七边形内角和:(7-2)×180=900(度)
填表如下:
图形名称 边数 图形 分成的三角个数 内角和
三角形 3 1 180度
四边形 4 2 360度
五边形 5 3 540度
六边形 6 4 720度
七边形 7 5 900度
……
我发现:多边形内角和为:(边数-2)乘180度,边数大于等于3。
22.(1)见详解;
(2)40;
(3)180;见详解
【分析】(1)作线段CB的延长线,从A点向CB的延长线作垂线,标记为点D, AD即为三角形ABC底边上的高,据此作答;
(2)根据三角形的内角和=180°,在三角形ABC中,∠B=120°,∠A=20°,那么∠C=180°-120°-20°,据此作答。
(3)验证三角形的内角和等于180°,可以用拼接法,先把三角形的三个角剪下来,再拼一拼,看看是否能拼成一个平角,据此作答。
【详解】(1)作图如下:
(2)180°-120°-20°
=60°-20°
=40°
所以∠C=40°。
(3)理由如下:
如图,拼接成了一个平角,所以可以证明三角形的内角和是180°。
23.①见详解
②5
【分析】①根据图数出多边形的边数以及分割成的三角形个数和四边形的个数即可;
②由于一个四边形可以分割成两个三角形,多边形的边数是5的时候,相当于可以分割3个三角形;六边形相当于可以分割4个三角形;七边形相当于可以分割5个三角形,由此即可知道多边形的变数减去2即可求出分割的三角形个数,再除以2即可求出分割的四边形的个数,据此即可求解。
【详解】由分析可知:①
多边形 ……
多边形的边数 5 6 7 8 9 10 …
分割 结果 三角形个数 1 0 1 0 1 0 …
四边形个数 1 2 2 3 3 4 …
②12-2=10
10÷2=5(个)
所以十二边形中最多能分割成5个四边形来计算内角和。
【点睛】本题主要考查平面图形的分割,同时要清楚四边形和三角形的关系是解题的关键。
答案第1页,共2页
答案第1页,共2页
