八年级数学上册试题 第12章 一次函数 单元测试提高卷 沪科版(含解析)
文档属性
| 名称 | 八年级数学上册试题 第12章 一次函数 单元测试提高卷 沪科版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 00:00:00 | ||
图片预览





文档简介
第12章《一次函数》(单元测试提高卷)
一.选择题(共10小题,每题4分,共计40分)
1.下列函数中,属于正比例函数的是( )
A.y=x2+1 B. C.y=5﹣2x D.
2.函数y=﹣2x+π的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.二、三、四象限 D.第一、三、四象限
3.在同一坐标系中,函数y=2kx与y=x﹣k的图象大致是( )
A. B.
C. D.
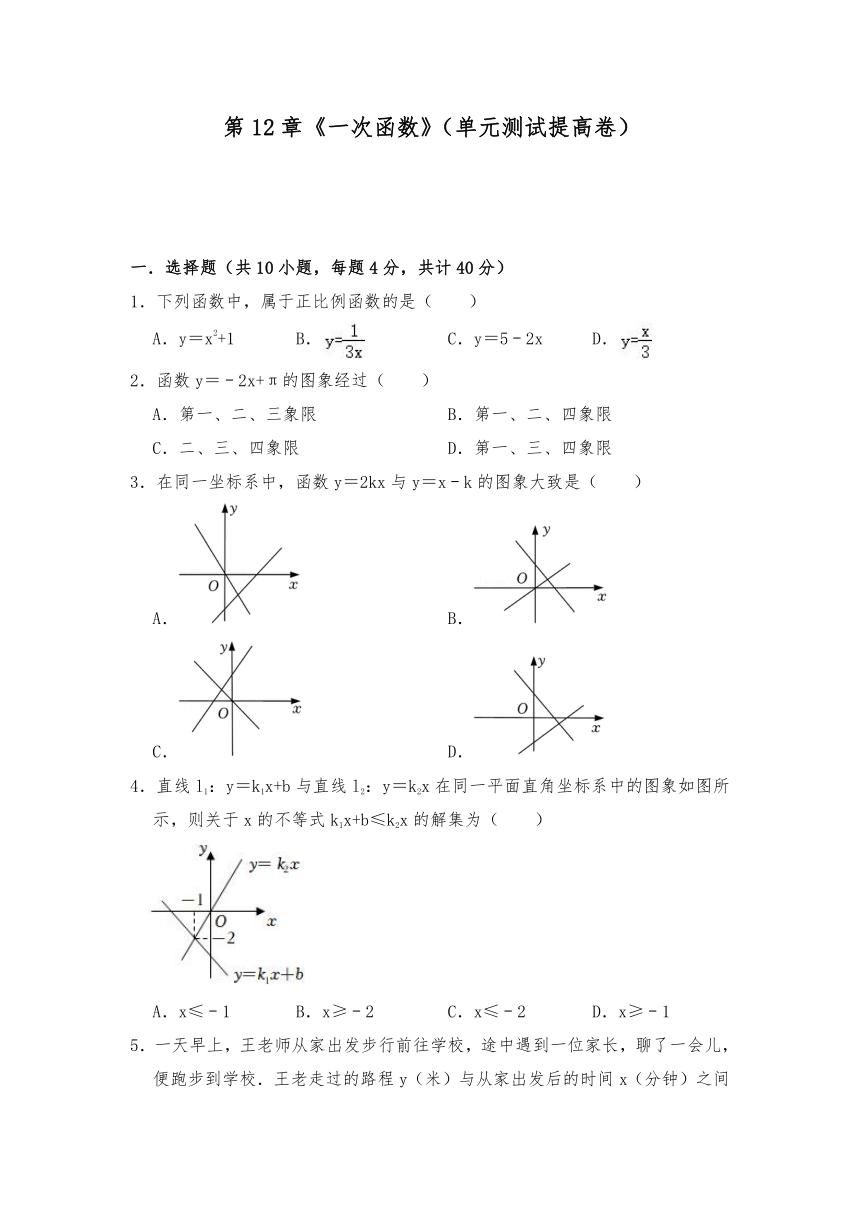
4.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b≤k2x的解集为( )
A.x≤﹣1 B.x≥﹣2 C.x≤﹣2 D.x≥﹣1
5.一天早上,王老师从家出发步行前往学校,途中遇到一位家长,聊了一会儿,便跑步到学校.王老走过的路程y(米)与从家出发后的时间x(分钟)之间关系如图所示.下列根据图象得到的信息,错误的是( )
A.王老师的家与学校之间路程为1千米
B.王老师与家长聊天时间经历了10分钟
C.若王老师没与家长聊天,保持原来的步行速度,可提前10分钟到达学校
D.王老师后面跑步的速度是开头步行速度的2倍
6.已知一次函数y=x+m与y=﹣+n的图象都经过点A(﹣2,0),且与y轴分别交于B,C两点,则△ABC的面积是( )
A.2 B.3 C.4 D.5
7.一次函数y=kx+b(k,b为常数)的图象经过点P(﹣2,﹣1)且y随着x的增大而减小,则该图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.甲乙两队举行一年一度的端午节赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示.下列说法:
(1)乙队率先到达终点;
(2)乙队比甲队少用了0.2分钟;
(3)出发时甲队比乙队速度大;
(4)两队在t=3.4分钟时相遇.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图1,在矩形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止.已知点P的运动速度为1cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则矩形对角线AC的长为( )
A.5 B.6 C.8 D.10
10.如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
二.填空题(共4小题,每题5分,共计20分)
11.若函数y=(m+2)xm2﹣3+5是一次函数,则m的值是 .
12.已知点(﹣3,y1)、(2,y2)、(1,3)在一次函数y=2x+5的图象上,则y1、y2的大小关系是 .
13.如图,直线y1=﹣x+a与y2=bx﹣4相交于点P(1,﹣3),则关于x的不等式﹣x+a<bx﹣4<0的解集是 .
14.小明和小亮分别从同一直线跑道A、B两端同时相向匀速出发,第一次相遇后小明觉得自己速度太慢便立即提速至原速的1.5倍,然后匀速运动到B端,且小明到达B端后立即以提速后的速度调头返回.小亮匀速跑步到A端后,立即按原速返回(忽略小明、小亮调头时间),当小明、小亮再次相遇时二人停止运动.已知两人相距的距离y(米)与小亮出发时间x(秒)之间的关系如图所示,则第二次相遇时小明与B端的距离为 米.
解答题(共9小题,15、16、17、18每题8分,19、20每题10分,21、22每题12分,23题14分,总共90分)
15.已知某一次函数的图象经过点A(0,2),B(1,3),C(a,1)三点,求a的值.
16.如图,表示李军从家到超市的时间与他离家的距离之间的关系.
(1)图象表示的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)李军到达超市用了多少时间?
(3)李军出发20分钟到30分钟内可能在做什么?
(4)李军从家到超市的平均速度是多少?返回时的平均速度是什么?
17.如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4),求直线l1的解析式.
18.已知y﹣4与x成正比,当x=1时,y=3.
(1)求y与x之间的函数关系式;
(2)当x=﹣2时,求函数y的值;
(3)将所得函数的图象向左平移a个单位,使它过点(0,﹣2),请求出a的值.
19.炎热的夏天,西瓜深受人们的青睐.某超市批发A,B两种西瓜共600千克进行销售,售价与进价如表所示:
名称 A种西瓜 B种西瓜
进价(元/千克) 4 3
售价(元/千克) 6 4
设A种西瓜批发x千克,全部售完后总利润为y元.
(1)求y与x的函数关系式;
(2)若购进A种西瓜不少于B种西瓜的2倍.求这批西瓜全部售出后最小利润是多少元?
20.夏季来临,某商场准备购进甲、乙两种空调,其中甲种空调比乙种空调进价每台少500元,用40000元购进甲种空调数量与用50000元购进乙种空调数量相同.该商场计划一次性从空调生产厂家购进甲、乙两种空调共100台,其中乙种空调的数量不超过甲种空调的2倍.若甲种空调每台售价2400元,乙种空调每台售价3000元.请解答下列问题:
(1)求甲、乙两种空调每台的进价分别是多少元?
(2)设购进甲种空调x台,100台空调的销售总利润为y元,该商店购进甲、乙两种空调各多少台才能使销售总利润最大,最大利润是多少?
(3)在(2)的条件下,商场拿出一部分利润购买A、B两种轮椅捐赠给敬老院,已知A种轮椅一台300元,B种轮椅一台400元,最后商场仅剩利润38600元,请直接写出商场有几种购买方案.
21.甲骑摩托车和乙驾驶汽车由A地到B地行驶90千米,行驶的路程y(千米)与经过的时间x(小时)之间的关系如图表示.请根据图象填空:
(1)摩托车的速度为 千米/小时;汽车的速度为 千米/小时;
(2)乙到达B地时,求甲离B地多少千米?
(3)在汽车出发几小时后,汽车和摩托车相遇?请说明理由.
22.某通讯公司就手机流量套餐推出两种方案,如下表:
方案一 方案二
每月基本费用(元) 90 110
每月免费使用流量(G) 25 40
超出后每G收费(元) 超过25G后,按照2元/G收费,套餐外流量使用费用达到70元封顶. 超过40G后,超出部分按照a元/G收费.
两种方案每月所需费用y(元)与每月使用流量x(G)之间的函数图象如图所示:
(1)填空:m= ,n= ,a= ;
(2)在方案二中,当每月使用流量超过40G时,求每月所需费用y(元)与每月使用流量x(G)之间的函数关系式;
(3)结合图象,在这两种方案中,当每月使用流量x为多少时,选择方案二更划算?请说明理由.
23.综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由.
答案
一.选择题
1.
【分析】根据正比例函数的定义逐个判断即可.
【解答】解:A.是二次函数,不是正比例函数,故本选项不符合题意;
B.是反比例函数,不是正比例函数,故本选项不符合题意;
C.是一次函数,但不是正比例函数,故本选项不符合题意;
D.是正比例函数,故本选项符合题意.
故选:D.
2.
【分析】根据一次函数图象的性质分析即可.
【解答】解:y=﹣2x+π,
K=﹣2<0,b=π>0,
所以该函数的图象经过一、二、四象限.
故选:B.
3.
【分析】分k>0及k<0两种情况考虑,当k>0时,利用正比例函数的性质及一次函数图象与系数的关系,可找出函数y=2kx与y=x﹣k的图象经过的象限;当k<0时,利用正比例函数的性质及一次函数图象与系数的关系,可找出函数y=2kx与y=x﹣k的图象经过的象限.
【解答】解:当k>0时,正比例函数y=kx的图象经过第一、三象限,一次函数y=x﹣k的图象经过第一、三、四象限;
当k<0时,正比例函数y=kx的图象经过第二、四象限,一次函数y=x﹣k的图象经过第一、二、三象限.
故选:C.
4.
【分析】看交点的哪一边,相对于相同的x值,直线y=k2x对应的函数值较大即可.
【解答】解:由图象可以看出,在交点的右侧,相同的x值,y=k2x对应的函数值较大,
∴不等式k1x+b≤k2x的解集为x≥﹣1,
故选:D.
5.
【分析】根据图象,由路程=速度×时间之间的关系逐项分析即可.
【解答】解:由图象可知王老师的家与学校之间的路程为1千米,故A正确,不符合题意;
王老师与家长聊天的时间为20﹣10=10(分钟),故B正确,不符合题意;
王老师原来的速度为500÷10=50米/分,
∴王老师不与家长聊天直接到学校可用时间为1000÷50=20(分),
∴王老师不与家长聊天可提前25﹣20=5(分钟)到学校,故C错误,符合题意;
王老师跑步的速度为:(1000﹣500)÷(25﹣20)=100(米/分),
∴王老师后面跑步的速度是开头步行速度的2倍,故D正确,不符合题意.
故选:C.
6.
【分析】首先分别把(﹣2,0)代入两个函数解析式中,解得m=3,n=﹣1,即得B(0,3),C(0,﹣1),然后根据三点坐标求△ABC的面积.
【解答】解:把(﹣2,0)代入两个函数解析式中,
得:m=3,n=﹣1,
∴B(0,3),C(0,﹣1),
∴S△ABC=×2×(3+1)=4.
故选:C.
7.
【分析】利用一次函数图象上点的坐标特征及一次函数的性质可得出k<0,b<0,再利用一次函数图象与系数的关系,即可得出一次函数y=kx+b的图象经过第二、三、四象限,即一次函数y=kx+b的图象不经过第一象限.
【解答】解:∵一次函数y=kx+b的图象经过点P(﹣2,﹣1),
∴﹣1=﹣2k+b,
∴b=2k﹣1.
∵y随着x的增大而减小,
∴k<0,
∴2k﹣1<0,即b<0,
∴一次函数y=kx+b的图象经过第二、三、四象限,
∴一次函数y=kx+b的图象不经过第一象限.
故选:A.
8.
【分析】根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,本题得以解决.
【解答】解:由图象可得,
乙队率先到达终点,故(1)正确,符合题意;
乙队比甲队少用了4﹣3.8=0.2(分钟),故(2)正确,符合题意;
出发时甲队比乙队速度大,故(3)正确,符合题意;
设甲队对应的函数解析式为y=kx,
∵点(4,1000)在该函数图象上,
∴1000=4k,
解得k=250,
即甲队对应的函数解析式为y=250x,
当2.2≤x≤3.8时,设乙队对应的函数解析式为y=ax+b,
∵(2.2,400),(3.8,1000)在该函数图象上,
∴,
解得,
即当2.2≤x≤3.8时,乙队对应的函数解析式为y=375x﹣425,
,
解得,
即两队在t=3.4分钟时相遇,故(4)正确,符合题意;
故选:D.
9.
【分析】根据△ABP的面积只与点P的位置有关,结合图2求出长方形的长和宽,再由勾股定理计算即可.
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,
当点P在点B,C之间运动时,△ABP的面积随时间x的增大而增大,
由图2知,当x=3时,点P到达点C处,
∴BC=3×2=6(cm);
当点P运动到点C,D之间时,△ABP的面积不变,
由图2可知,点P从点C运动到点D所用时间为7﹣3=4(s),
∴CD=2×4=8(cm),
∴AC=(cm),
故选:D.
10.
【分析】由于P的纵坐标为2,故点P在直线y=2上,要求符合题意的m值,则P点为直线y=2与题目中两直线的交点,此时m存在最大值与最小值,故可求得.
【解答】解:∵点P(m,2)是△ABC内部(包括边上)的一点,
∴点P在直线y=2上,如图所示,
当P为直线y=2与直线y2的交点时,m取最大值,
当P为直线y=2与直线y1的交点时,m取最小值,
∵y2=﹣x+3中令y=2,则x=1,
y1=x+3中令y=2,则x=﹣1,
∴m的最大值为1,m的最小值为﹣1.
则m的最大值与最小值之差为:1﹣(﹣1)=2.
故选:B.
二.填空题(共4小题)
11.
【分析】根据一次函数的定义得出m2﹣3=1且m=2≠0,再求出m即可.
【解答】解:∵函数y=(m+2)+5是一次函数,
∴m2﹣3=1且m+2≠0,
解得:m=2.
故答案为:2.
12.
【分析】根据一次函数解析式可知k>0,可得y随着x增大而x增大,根据x的值即可进行比较.
【解答】解:在一次函数y=2x+5中,
∵k=2>0,
∴y随着x增大而增大,
∵﹣3<2,
∴y1<y2,
故答案为:y1<y2.
13.
【分析】观察函数图象得到当1<x<4时,函数y=﹣x+a的图象都在y=bx﹣4的图象下方,y=bx﹣4的图象在x轴的下方,所以不等式﹣x+a<bx﹣4<0的解集为1<x<4.
【解答】解:如图,设直线y2=bx﹣4与x轴相交于点Q,
把P(1,﹣3)代入y2=bx﹣4,得﹣3=b﹣4.
解得b=1.
则y2=x﹣4.
令y=0,则x=4.
∴Q(0,4).
∵直线y1=﹣x+a与y2=bx﹣4相交于点P(1,﹣3),
∴关于x的不等式﹣x+a<bx﹣4<0的解集是 1<x<4.
故答案是:1<x<4.
14.
【分析】根据第一次相遇用60秒和第一次相遇后两人速度相同,列出方程组即可求解.
【解答】解:设开始小明和小亮的速度分别为:a、b,则小明加速后的速度为1.5a,
两人第一次相遇的时间为60秒,故60(a+b)=600①;
在100秒后一段时间,小明和小亮的速度分别为:1.5a,b,此时两人的距离保持不变,说明此时的两人的速度相同,即1.5a=b②,
联立①②并解得:,即开始小明和小亮的速度分别为4米/秒和6米/秒;
第一次相遇时,小明走的距离为4×60=240(米),
则小明到达B地的时间为60+=120(秒),
小明到达B地到第二次相遇的时间为=40(秒),
故第二次相遇时,小明距离B地的距离为40×6=240(米).
故答案为240.
三.解答题
15.解:设一次函数的解析式为y=kx+b,
将点A(0,2),B(1,3)分别代入解析式得,
解得,
则函数解析式为y=x+2,
将C(a,1)代入解析式得,a+2=1,
解得a=﹣1,
故a的值为﹣1.
16.解:(1)图象表示的是李军从家到超市的时间与他离家的距离两个变量之间的关系,时间为自变量,离家的距离为因变量;
(2)李军到达超市用了20分钟;
(3)李军出发20分钟到30分钟内可能在吃早餐.(答案部唯一);
(4)李军从家到超市的平均速度是=45(米/分),返回时的平均速度是=60(米/分).
17.解:∵点B在直线l2上,
∴4=2m,得m=2,
∴B(2,4),
设直线l1的解析式为y=kx+b,
由题意得,
解得,
∴l1的解析式为.
18.解:(1)设y﹣4=kx,
∵当x=1时,y=3,
∴3﹣4=k,
解得k=﹣1,
∴y﹣4=﹣x,
∴y与x之间的函数关系式为y=﹣x+4;
(2)把x=﹣2代入y=﹣x+4得,y=2+4,
∴y=6.
(3)将所得函数的图象向左平移a个单位,所得函数图象的解析式是y=﹣(x+a)+4,
∵过点(0,﹣2),
∴﹣2=﹣a+4,
解得a=6.
19.解:(1)A种西瓜批发x千克,则B种西瓜批发(600﹣x) 千克,
根据题意得:y=(6﹣4)x+(4﹣3)(600﹣x )=x+600,
∴y与x的函数关系式为y=x+600;
(2)∵购进A种西瓜不少B种西瓜的2倍,
∴x≥2(600﹣x),
解得x≥400,
∵1>0,
∴y随x的增大而增大,
∴当x=400时,y的值最小,最小值为y=400+600=1000,
∴这批西瓜全部售出后最小利润是1000元.
20.解:(1)设甲种空调每台的进价m元,则乙种空调每台的进价(m+500)元,
由题意得:,
解得m=2000,
经检验m=2000是原分式方程的解,
∴m+500=2500,
答:甲、乙两种空调每台的进价分别是2000元和2500元;
(2)根据题意,y=(2400﹣2000)x+(3000﹣2500)(100﹣x)=﹣100x+50000,
∵乙种空调的数量不超过甲种空调的2倍,
∴100﹣x≤2x,
解得x≥,
在y=﹣100x+50000中,
∵k=﹣100<0,
∴y随x的增大而减小,
∵x为整数,
∴x=34时,y取得最大值,最大值为﹣100×34+50000=46600,
此时100﹣x=100﹣34=66,
答:商店购进甲种空调34台,乙种空调66台,才能使总利润最大,最大利润是46600元;
(3)设A种轮椅购买a台,B种轮椅购买b台,
根据题意得:300a+400b=46600﹣38600,
∴b=20﹣a,
∵a,b是正整数,
∴20﹣a>0,且a是4的倍数,
∴或或或或或,
∴商场有6种购买方案.
21.解:(1)摩托车的速度为:90÷5=18千米/小时,
汽车的速度为:90÷(4﹣2)=45千米/小时,
故答案为:18、45;
(2)5﹣4=1,
乙比甲早1小时到达B地,
此时甲距离B地还有:1×18=18(千米);
(3)在汽车出发后小时,汽车和摩托车相遇,
理由:设在汽车出发后x小时,汽车和摩托车相遇,
45x=18(x+2),
解得x=,
∴在汽车出发后小时,汽车和摩托车相遇.
22.解:(1)方案一套餐外流量使用费用达到70元封顶,
∴m=90+70=160;
∵方案一超过25G后,按照2元/G收费,
∴2(n﹣25)=70,解得:n=60;
∵方案二超过40G后,超出部分按照a元/G收费,
∴a==2.5,
故答案为:160;60;2.5.
(2)在方案二中,当每月流量超过40G时,y是x的一次函数且经过(40,110)(60,160),
设函数关系式为y=kx+b,将(40,110)(60,160)代入,得:
,
解得:,
所以y与x的函数关系为y=x+10.
(3)由题意可得:在方案一中,
当25≤x≤60时,y与x的函数关系为y=90+(x﹣25)×2=2x+40,
将y=110代入y=2x+40中,2x+40=110,解得x=35,
观察图像得:当35<x<60时,方案二的图像位于方案一的下方,
所以当35<x<60时,方案二更划算.
23.解:(1)当x=0时,y=x+3=3,
∴点B坐标为(0,3),
当y=x+3=0时,x=﹣6,
∴点A坐标为(﹣6,0);
(2)将点B坐标代入y=﹣x+b,
得b=3,
∴直线BC的表达式:y=﹣x+3,
当y=﹣x+3=0时,x=3,
∴点C(3,0);
(3)存在以A,C,P为顶点的三角形的面积为18,
∵A(﹣6,0),点C(3,0),
∴AC=9,
∴=18,
∴|Py|=4,
当y=x+3=4时,x=2,
∴点P坐标为(2,4),
当y=x+3=﹣4时,x=﹣14,
∴点P坐标为(﹣14,﹣4),
综上,满足条件的点P坐标为(2,4)或(﹣14,﹣4).
一.选择题(共10小题,每题4分,共计40分)
1.下列函数中,属于正比例函数的是( )
A.y=x2+1 B. C.y=5﹣2x D.
2.函数y=﹣2x+π的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.二、三、四象限 D.第一、三、四象限
3.在同一坐标系中,函数y=2kx与y=x﹣k的图象大致是( )
A. B.
C. D.
4.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b≤k2x的解集为( )
A.x≤﹣1 B.x≥﹣2 C.x≤﹣2 D.x≥﹣1
5.一天早上,王老师从家出发步行前往学校,途中遇到一位家长,聊了一会儿,便跑步到学校.王老走过的路程y(米)与从家出发后的时间x(分钟)之间关系如图所示.下列根据图象得到的信息,错误的是( )
A.王老师的家与学校之间路程为1千米
B.王老师与家长聊天时间经历了10分钟
C.若王老师没与家长聊天,保持原来的步行速度,可提前10分钟到达学校
D.王老师后面跑步的速度是开头步行速度的2倍
6.已知一次函数y=x+m与y=﹣+n的图象都经过点A(﹣2,0),且与y轴分别交于B,C两点,则△ABC的面积是( )
A.2 B.3 C.4 D.5
7.一次函数y=kx+b(k,b为常数)的图象经过点P(﹣2,﹣1)且y随着x的增大而减小,则该图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.甲乙两队举行一年一度的端午节赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示.下列说法:
(1)乙队率先到达终点;
(2)乙队比甲队少用了0.2分钟;
(3)出发时甲队比乙队速度大;
(4)两队在t=3.4分钟时相遇.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.如图1,在矩形ABCD中,动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止.已知点P的运动速度为1cm/s,设点P的运动时间为x(s),△PAB的面积为y(cm2),若y关于x的函数图象如图2所示,则矩形对角线AC的长为( )
A.5 B.6 C.8 D.10
10.如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.1 B.2 C.4 D.6
二.填空题(共4小题,每题5分,共计20分)
11.若函数y=(m+2)xm2﹣3+5是一次函数,则m的值是 .
12.已知点(﹣3,y1)、(2,y2)、(1,3)在一次函数y=2x+5的图象上,则y1、y2的大小关系是 .
13.如图,直线y1=﹣x+a与y2=bx﹣4相交于点P(1,﹣3),则关于x的不等式﹣x+a<bx﹣4<0的解集是 .
14.小明和小亮分别从同一直线跑道A、B两端同时相向匀速出发,第一次相遇后小明觉得自己速度太慢便立即提速至原速的1.5倍,然后匀速运动到B端,且小明到达B端后立即以提速后的速度调头返回.小亮匀速跑步到A端后,立即按原速返回(忽略小明、小亮调头时间),当小明、小亮再次相遇时二人停止运动.已知两人相距的距离y(米)与小亮出发时间x(秒)之间的关系如图所示,则第二次相遇时小明与B端的距离为 米.
解答题(共9小题,15、16、17、18每题8分,19、20每题10分,21、22每题12分,23题14分,总共90分)
15.已知某一次函数的图象经过点A(0,2),B(1,3),C(a,1)三点,求a的值.
16.如图,表示李军从家到超市的时间与他离家的距离之间的关系.
(1)图象表示的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)李军到达超市用了多少时间?
(3)李军出发20分钟到30分钟内可能在做什么?
(4)李军从家到超市的平均速度是多少?返回时的平均速度是什么?
17.如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4),求直线l1的解析式.
18.已知y﹣4与x成正比,当x=1时,y=3.
(1)求y与x之间的函数关系式;
(2)当x=﹣2时,求函数y的值;
(3)将所得函数的图象向左平移a个单位,使它过点(0,﹣2),请求出a的值.
19.炎热的夏天,西瓜深受人们的青睐.某超市批发A,B两种西瓜共600千克进行销售,售价与进价如表所示:
名称 A种西瓜 B种西瓜
进价(元/千克) 4 3
售价(元/千克) 6 4
设A种西瓜批发x千克,全部售完后总利润为y元.
(1)求y与x的函数关系式;
(2)若购进A种西瓜不少于B种西瓜的2倍.求这批西瓜全部售出后最小利润是多少元?
20.夏季来临,某商场准备购进甲、乙两种空调,其中甲种空调比乙种空调进价每台少500元,用40000元购进甲种空调数量与用50000元购进乙种空调数量相同.该商场计划一次性从空调生产厂家购进甲、乙两种空调共100台,其中乙种空调的数量不超过甲种空调的2倍.若甲种空调每台售价2400元,乙种空调每台售价3000元.请解答下列问题:
(1)求甲、乙两种空调每台的进价分别是多少元?
(2)设购进甲种空调x台,100台空调的销售总利润为y元,该商店购进甲、乙两种空调各多少台才能使销售总利润最大,最大利润是多少?
(3)在(2)的条件下,商场拿出一部分利润购买A、B两种轮椅捐赠给敬老院,已知A种轮椅一台300元,B种轮椅一台400元,最后商场仅剩利润38600元,请直接写出商场有几种购买方案.
21.甲骑摩托车和乙驾驶汽车由A地到B地行驶90千米,行驶的路程y(千米)与经过的时间x(小时)之间的关系如图表示.请根据图象填空:
(1)摩托车的速度为 千米/小时;汽车的速度为 千米/小时;
(2)乙到达B地时,求甲离B地多少千米?
(3)在汽车出发几小时后,汽车和摩托车相遇?请说明理由.
22.某通讯公司就手机流量套餐推出两种方案,如下表:
方案一 方案二
每月基本费用(元) 90 110
每月免费使用流量(G) 25 40
超出后每G收费(元) 超过25G后,按照2元/G收费,套餐外流量使用费用达到70元封顶. 超过40G后,超出部分按照a元/G收费.
两种方案每月所需费用y(元)与每月使用流量x(G)之间的函数图象如图所示:
(1)填空:m= ,n= ,a= ;
(2)在方案二中,当每月使用流量超过40G时,求每月所需费用y(元)与每月使用流量x(G)之间的函数关系式;
(3)结合图象,在这两种方案中,当每月使用流量x为多少时,选择方案二更划算?请说明理由.
23.综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由.
答案
一.选择题
1.
【分析】根据正比例函数的定义逐个判断即可.
【解答】解:A.是二次函数,不是正比例函数,故本选项不符合题意;
B.是反比例函数,不是正比例函数,故本选项不符合题意;
C.是一次函数,但不是正比例函数,故本选项不符合题意;
D.是正比例函数,故本选项符合题意.
故选:D.
2.
【分析】根据一次函数图象的性质分析即可.
【解答】解:y=﹣2x+π,
K=﹣2<0,b=π>0,
所以该函数的图象经过一、二、四象限.
故选:B.
3.
【分析】分k>0及k<0两种情况考虑,当k>0时,利用正比例函数的性质及一次函数图象与系数的关系,可找出函数y=2kx与y=x﹣k的图象经过的象限;当k<0时,利用正比例函数的性质及一次函数图象与系数的关系,可找出函数y=2kx与y=x﹣k的图象经过的象限.
【解答】解:当k>0时,正比例函数y=kx的图象经过第一、三象限,一次函数y=x﹣k的图象经过第一、三、四象限;
当k<0时,正比例函数y=kx的图象经过第二、四象限,一次函数y=x﹣k的图象经过第一、二、三象限.
故选:C.
4.
【分析】看交点的哪一边,相对于相同的x值,直线y=k2x对应的函数值较大即可.
【解答】解:由图象可以看出,在交点的右侧,相同的x值,y=k2x对应的函数值较大,
∴不等式k1x+b≤k2x的解集为x≥﹣1,
故选:D.
5.
【分析】根据图象,由路程=速度×时间之间的关系逐项分析即可.
【解答】解:由图象可知王老师的家与学校之间的路程为1千米,故A正确,不符合题意;
王老师与家长聊天的时间为20﹣10=10(分钟),故B正确,不符合题意;
王老师原来的速度为500÷10=50米/分,
∴王老师不与家长聊天直接到学校可用时间为1000÷50=20(分),
∴王老师不与家长聊天可提前25﹣20=5(分钟)到学校,故C错误,符合题意;
王老师跑步的速度为:(1000﹣500)÷(25﹣20)=100(米/分),
∴王老师后面跑步的速度是开头步行速度的2倍,故D正确,不符合题意.
故选:C.
6.
【分析】首先分别把(﹣2,0)代入两个函数解析式中,解得m=3,n=﹣1,即得B(0,3),C(0,﹣1),然后根据三点坐标求△ABC的面积.
【解答】解:把(﹣2,0)代入两个函数解析式中,
得:m=3,n=﹣1,
∴B(0,3),C(0,﹣1),
∴S△ABC=×2×(3+1)=4.
故选:C.
7.
【分析】利用一次函数图象上点的坐标特征及一次函数的性质可得出k<0,b<0,再利用一次函数图象与系数的关系,即可得出一次函数y=kx+b的图象经过第二、三、四象限,即一次函数y=kx+b的图象不经过第一象限.
【解答】解:∵一次函数y=kx+b的图象经过点P(﹣2,﹣1),
∴﹣1=﹣2k+b,
∴b=2k﹣1.
∵y随着x的增大而减小,
∴k<0,
∴2k﹣1<0,即b<0,
∴一次函数y=kx+b的图象经过第二、三、四象限,
∴一次函数y=kx+b的图象不经过第一象限.
故选:A.
8.
【分析】根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,本题得以解决.
【解答】解:由图象可得,
乙队率先到达终点,故(1)正确,符合题意;
乙队比甲队少用了4﹣3.8=0.2(分钟),故(2)正确,符合题意;
出发时甲队比乙队速度大,故(3)正确,符合题意;
设甲队对应的函数解析式为y=kx,
∵点(4,1000)在该函数图象上,
∴1000=4k,
解得k=250,
即甲队对应的函数解析式为y=250x,
当2.2≤x≤3.8时,设乙队对应的函数解析式为y=ax+b,
∵(2.2,400),(3.8,1000)在该函数图象上,
∴,
解得,
即当2.2≤x≤3.8时,乙队对应的函数解析式为y=375x﹣425,
,
解得,
即两队在t=3.4分钟时相遇,故(4)正确,符合题意;
故选:D.
9.
【分析】根据△ABP的面积只与点P的位置有关,结合图2求出长方形的长和宽,再由勾股定理计算即可.
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,
当点P在点B,C之间运动时,△ABP的面积随时间x的增大而增大,
由图2知,当x=3时,点P到达点C处,
∴BC=3×2=6(cm);
当点P运动到点C,D之间时,△ABP的面积不变,
由图2可知,点P从点C运动到点D所用时间为7﹣3=4(s),
∴CD=2×4=8(cm),
∴AC=(cm),
故选:D.
10.
【分析】由于P的纵坐标为2,故点P在直线y=2上,要求符合题意的m值,则P点为直线y=2与题目中两直线的交点,此时m存在最大值与最小值,故可求得.
【解答】解:∵点P(m,2)是△ABC内部(包括边上)的一点,
∴点P在直线y=2上,如图所示,
当P为直线y=2与直线y2的交点时,m取最大值,
当P为直线y=2与直线y1的交点时,m取最小值,
∵y2=﹣x+3中令y=2,则x=1,
y1=x+3中令y=2,则x=﹣1,
∴m的最大值为1,m的最小值为﹣1.
则m的最大值与最小值之差为:1﹣(﹣1)=2.
故选:B.
二.填空题(共4小题)
11.
【分析】根据一次函数的定义得出m2﹣3=1且m=2≠0,再求出m即可.
【解答】解:∵函数y=(m+2)+5是一次函数,
∴m2﹣3=1且m+2≠0,
解得:m=2.
故答案为:2.
12.
【分析】根据一次函数解析式可知k>0,可得y随着x增大而x增大,根据x的值即可进行比较.
【解答】解:在一次函数y=2x+5中,
∵k=2>0,
∴y随着x增大而增大,
∵﹣3<2,
∴y1<y2,
故答案为:y1<y2.
13.
【分析】观察函数图象得到当1<x<4时,函数y=﹣x+a的图象都在y=bx﹣4的图象下方,y=bx﹣4的图象在x轴的下方,所以不等式﹣x+a<bx﹣4<0的解集为1<x<4.
【解答】解:如图,设直线y2=bx﹣4与x轴相交于点Q,
把P(1,﹣3)代入y2=bx﹣4,得﹣3=b﹣4.
解得b=1.
则y2=x﹣4.
令y=0,则x=4.
∴Q(0,4).
∵直线y1=﹣x+a与y2=bx﹣4相交于点P(1,﹣3),
∴关于x的不等式﹣x+a<bx﹣4<0的解集是 1<x<4.
故答案是:1<x<4.
14.
【分析】根据第一次相遇用60秒和第一次相遇后两人速度相同,列出方程组即可求解.
【解答】解:设开始小明和小亮的速度分别为:a、b,则小明加速后的速度为1.5a,
两人第一次相遇的时间为60秒,故60(a+b)=600①;
在100秒后一段时间,小明和小亮的速度分别为:1.5a,b,此时两人的距离保持不变,说明此时的两人的速度相同,即1.5a=b②,
联立①②并解得:,即开始小明和小亮的速度分别为4米/秒和6米/秒;
第一次相遇时,小明走的距离为4×60=240(米),
则小明到达B地的时间为60+=120(秒),
小明到达B地到第二次相遇的时间为=40(秒),
故第二次相遇时,小明距离B地的距离为40×6=240(米).
故答案为240.
三.解答题
15.解:设一次函数的解析式为y=kx+b,
将点A(0,2),B(1,3)分别代入解析式得,
解得,
则函数解析式为y=x+2,
将C(a,1)代入解析式得,a+2=1,
解得a=﹣1,
故a的值为﹣1.
16.解:(1)图象表示的是李军从家到超市的时间与他离家的距离两个变量之间的关系,时间为自变量,离家的距离为因变量;
(2)李军到达超市用了20分钟;
(3)李军出发20分钟到30分钟内可能在吃早餐.(答案部唯一);
(4)李军从家到超市的平均速度是=45(米/分),返回时的平均速度是=60(米/分).
17.解:∵点B在直线l2上,
∴4=2m,得m=2,
∴B(2,4),
设直线l1的解析式为y=kx+b,
由题意得,
解得,
∴l1的解析式为.
18.解:(1)设y﹣4=kx,
∵当x=1时,y=3,
∴3﹣4=k,
解得k=﹣1,
∴y﹣4=﹣x,
∴y与x之间的函数关系式为y=﹣x+4;
(2)把x=﹣2代入y=﹣x+4得,y=2+4,
∴y=6.
(3)将所得函数的图象向左平移a个单位,所得函数图象的解析式是y=﹣(x+a)+4,
∵过点(0,﹣2),
∴﹣2=﹣a+4,
解得a=6.
19.解:(1)A种西瓜批发x千克,则B种西瓜批发(600﹣x) 千克,
根据题意得:y=(6﹣4)x+(4﹣3)(600﹣x )=x+600,
∴y与x的函数关系式为y=x+600;
(2)∵购进A种西瓜不少B种西瓜的2倍,
∴x≥2(600﹣x),
解得x≥400,
∵1>0,
∴y随x的增大而增大,
∴当x=400时,y的值最小,最小值为y=400+600=1000,
∴这批西瓜全部售出后最小利润是1000元.
20.解:(1)设甲种空调每台的进价m元,则乙种空调每台的进价(m+500)元,
由题意得:,
解得m=2000,
经检验m=2000是原分式方程的解,
∴m+500=2500,
答:甲、乙两种空调每台的进价分别是2000元和2500元;
(2)根据题意,y=(2400﹣2000)x+(3000﹣2500)(100﹣x)=﹣100x+50000,
∵乙种空调的数量不超过甲种空调的2倍,
∴100﹣x≤2x,
解得x≥,
在y=﹣100x+50000中,
∵k=﹣100<0,
∴y随x的增大而减小,
∵x为整数,
∴x=34时,y取得最大值,最大值为﹣100×34+50000=46600,
此时100﹣x=100﹣34=66,
答:商店购进甲种空调34台,乙种空调66台,才能使总利润最大,最大利润是46600元;
(3)设A种轮椅购买a台,B种轮椅购买b台,
根据题意得:300a+400b=46600﹣38600,
∴b=20﹣a,
∵a,b是正整数,
∴20﹣a>0,且a是4的倍数,
∴或或或或或,
∴商场有6种购买方案.
21.解:(1)摩托车的速度为:90÷5=18千米/小时,
汽车的速度为:90÷(4﹣2)=45千米/小时,
故答案为:18、45;
(2)5﹣4=1,
乙比甲早1小时到达B地,
此时甲距离B地还有:1×18=18(千米);
(3)在汽车出发后小时,汽车和摩托车相遇,
理由:设在汽车出发后x小时,汽车和摩托车相遇,
45x=18(x+2),
解得x=,
∴在汽车出发后小时,汽车和摩托车相遇.
22.解:(1)方案一套餐外流量使用费用达到70元封顶,
∴m=90+70=160;
∵方案一超过25G后,按照2元/G收费,
∴2(n﹣25)=70,解得:n=60;
∵方案二超过40G后,超出部分按照a元/G收费,
∴a==2.5,
故答案为:160;60;2.5.
(2)在方案二中,当每月流量超过40G时,y是x的一次函数且经过(40,110)(60,160),
设函数关系式为y=kx+b,将(40,110)(60,160)代入,得:
,
解得:,
所以y与x的函数关系为y=x+10.
(3)由题意可得:在方案一中,
当25≤x≤60时,y与x的函数关系为y=90+(x﹣25)×2=2x+40,
将y=110代入y=2x+40中,2x+40=110,解得x=35,
观察图像得:当35<x<60时,方案二的图像位于方案一的下方,
所以当35<x<60时,方案二更划算.
23.解:(1)当x=0时,y=x+3=3,
∴点B坐标为(0,3),
当y=x+3=0时,x=﹣6,
∴点A坐标为(﹣6,0);
(2)将点B坐标代入y=﹣x+b,
得b=3,
∴直线BC的表达式:y=﹣x+3,
当y=﹣x+3=0时,x=3,
∴点C(3,0);
(3)存在以A,C,P为顶点的三角形的面积为18,
∵A(﹣6,0),点C(3,0),
∴AC=9,
∴=18,
∴|Py|=4,
当y=x+3=4时,x=2,
∴点P坐标为(2,4),
当y=x+3=﹣4时,x=﹣14,
∴点P坐标为(﹣14,﹣4),
综上,满足条件的点P坐标为(2,4)或(﹣14,﹣4).
