上海市黄浦区2015-2016学年八年级上学期期中数学试卷【解析版】
文档属性
| 名称 | 上海市黄浦区2015-2016学年八年级上学期期中数学试卷【解析版】 |

|
|
| 格式 | zip | ||
| 文件大小 | 319.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-09 00:00:00 | ||
图片预览




文档简介
2015-2016学年上海市黄浦区八年级(上)期中数学试卷
一、选择题
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.的一个有理化因式是( )
A. B. C.+ D.﹣
3.下列方程是一元二次方程的是( )
A.ax2﹣2x+=0(a是已知数) B.3x2+2x﹣4=3x2
C.5x2﹣2x=0 D.=1
4.下列二次根式中与是同类二次根式的是( )
A. B. C. D.
5.下列语句中哪个是命题( )
A.联结A、B两点 B.等角的余角相等吗?
C.对顶角相等 D.代数式(a≥0)叫二次根式
6.如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
( http: / / www.21cnjy.com )
A.∠BAC=36°
B.BD平分∠ABC
C.若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54°
D.点N是BD的中点
二、填空题(每小题2分,共24分)
7.计算:﹣=__________.
8.如果有意义,那么a的取值范围是__________.
9.化简:(b>0)=__________.
10.某种商品原价100元,经过两次降价后,该种商品的利润减少了36元,那么该商品平均每次降价的百分比是__________.
11.将命题“同角的补角相等”改写成“如果…那么…”形式为__________.
12.若x=﹣1是方程x2﹣mx﹣3=0的一个根,则m的值为__________.
13.在实数范围内因式分解:x2﹣4x﹣3=__________.
14.若|b﹣1|与互为相反数,则(a+b)2015=__________.
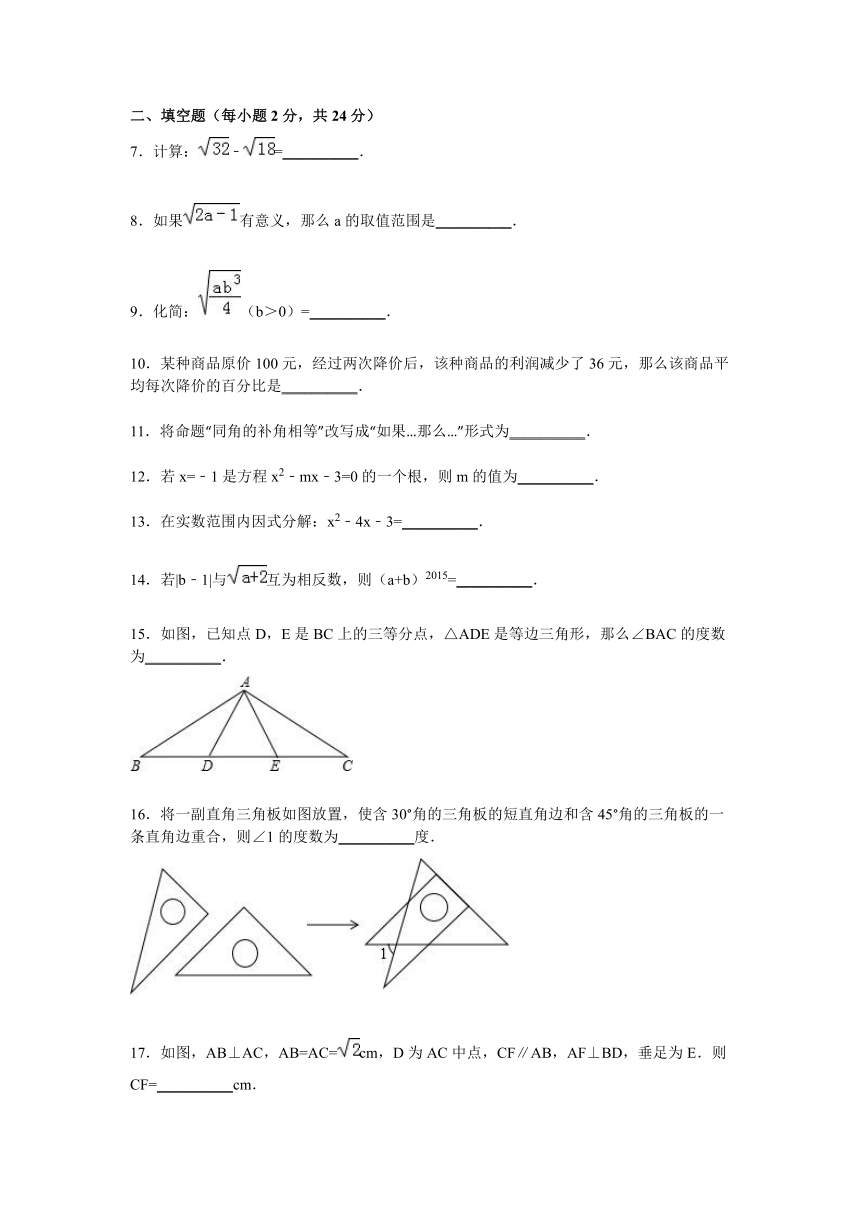
15.如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为__________.
( http: / / www.21cnjy.com )
16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为__________度.
( http: / / www.21cnjy.com )
17.如图,AB⊥AC,AB=AC=cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=__________cm.
( http: / / www.21cnjy.com )
18.已知等腰△ABC,AB=AC,∠C ( http: / / www.21cnjy.com )=30°,如果将△ABC绕着点B旋转,使点C正好落在直线AB上的点C′处,那么∠BC′C=__________度.
三、简答题(每小题7分,共56分)
19.计算:.
20.解方程:(x+3)(x﹣1)﹣5=0.
21.解方程:y﹣=﹣.
22.用配方法解方程:2x2﹣4x+1=0.
23.化简求值:当x=3,y=4时,求代数式+的值.
24.已知关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+1=0(m为常数)有两个实数根,求m的取值范围.
25.如图,要建一个面积为150㎡的长方形 ( http: / / www.21cnjy.com )养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:
(1)求鸡场的长和宽各为多少米?
(2)若将题中条件“墙长为18米”换为“墙 ( http: / / www.21cnjy.com )长为a米”,且增加条件“离墙9m开外鸡场一侧准备修条小路”,其他条件不变,则墙长a米至少要多少米?
( http: / / www.21cnjy.com )
26.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,且AB=CG,AC=BF.
(1)求证:△ABF≌△GCA;
(2)求证:AG⊥AF.
( http: / / www.21cnjy.com )
四、解答题
27.如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
(1)如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过3秒后,△BPD与△CQP是否全等?请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以(1)②中的 ( http: / / www.21cnjy.com )运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
( http: / / www.21cnjy.com )
2015-2016学年上海市黄浦区八年级(上)期中数学试卷
一、选择题
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
【考点】最简二次根式.
【专题】计算题;二次根式.
【分析】利用最简二次根式的定义判断即可.
【解答】解:A、是最简二次根式,正确;
B、=2,错误;
C、=|a|b2,错误;
D、=,错误,
故选A
【点评】此题考查了最简二次根式,熟练掌握最简二次根式的定义是解本题的关键.
2.的一个有理化因式是( )
A. B. C.+ D.﹣
【考点】分母有理化.
【专题】计算题;二次根式.
【分析】找出原式的一个有理化因式即可.
【解答】解:的一个有理化因式是,
故选B
【点评】此题考查了分母有理化,熟练掌握有理化因式的取法是解本题的关键.
3.下列方程是一元二次方程的是( )
A.ax2﹣2x+=0(a是已知数) B.3x2+2x﹣4=3x2
C.5x2﹣2x=0 D. ( http: / / www.21cnjy.com )=1
【考点】一元二次方程的定义.
【专题】计算题;一元二次方程及应用.
【分析】利用一元二次方程的定义判断即可.
【解答】解:5x2﹣2x=0是一元二次方程,
故选C
【点评】此题考查了一元二次方程的定义,熟练掌握一元二次方程的定义是解本题的关键.
4.下列二次根式中与是同类二次根式的是( )
A. B. C. D.
【考点】同类二次根式.
【专题】计算题.
【分析】根据化简成最简二次根式,被开方数相同的二次根式是同类二次根式,可得答案.
【解答】解:,
A、,故A不正确;
B、被开方数不同,故B不正确;
C、,故C正确;
D、,故D不正确;
故选:C.
【点评】本题考查了同类二次根式,先化成最简二次根式,再比较被开方数.
5.下列语句中哪个是命题( )
A.联结A、B两点 B.等角的余角相等吗?
C.对顶角相等 D.代数式(a≥0)叫二次根式
【考点】命题与定理.
【分析】判断一件事情的语句,叫做命题.根据命题的定义进行判断.
【解答】解:A、不能判断其真假,不构成命题,故本选项错误;
B、不能判断其真假,不构成命题,故本选项错误;
C、是,因为能够判断真假,故本选项正确;
D、代数式(a≥0)叫二次根式,是定义,不是命题,故本选项错误.
故选C.
【点评】本题主要考查了命题的定义:判断一件事情的语句是命题,一般有“是”,“不是”等判断词,比较简单.
6.如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
( http: / / www.21cnjy.com )
A.∠BAC=36°
B.BD平分∠ABC
C.若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54°
D.点N是BD的中点
【考点】等腰三角形的性质.
【分析】根据等腰三角形的性质得到∠AB ( http: / / www.21cnjy.com )C=∠C=∠BDC,∠BAC=∠ABD,由三角形的外角的性质得到∠BDC=∠BAC+∠ABD=2∠BAC,
推出∠ABC=∠C=2∠BAC,根据三角形的内角和列方程即可得到∠BAC=36°,故A正确;由∠ABD=∠BAC=36°,∠ABC==72°,即可得到BD平分∠ABC,故B正确;根据直角三角形的性质和等腰三角形的性质即可得到∠BNM=54°,故C正确;根据三角形的中位线的性质即可判断D错误,
【解答】解:∵AB=AC,AD=BD=BC,
∴∠ABC=∠C=∠BDC,∠BAC=∠ABD,
∵∠BDC=∠BAC+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∴∠BAC+∠ACB+∠ABC=∠BAC+2∠BAC+2∠BAC=180°,
∴∠BAC=36°,故A正确;
∴∠ABD=∠BAC=36°,
∠ABC==72°,
∴∠ABC=2∠ABD,
∴BD平分∠ABC,故B正确;
∵AB=AC,BM=CM,
∴AM⊥BC,
∴∠AMB=90°,
∵∠DBC=36°,
∴∠BNM=54°,故C正确;
∵AM不平行于AC,BM=CM,
∴BN≠DN,
∴D错误,
故选D.
【点评】本题考查了等腰三角形的性质,角平分线的定义,三角形的内角和,熟练掌握等腰三角形的性质是解题的关键.
二、填空题(每小题2分,共24分)
7.计算:﹣=.
【考点】二次根式的加减法.
【专题】计算题;二次根式.
【分析】原式各项化简后,合并即可得到结果.
【解答】解:原式=4﹣3=,
故答案为:
【点评】此题考查了二次根式的加减法,熟练掌握运算法则是解本题的关键.
8.如果有意义,那么a的取值范围是a≥.
【考点】二次根式有意义的条件.
【分析】根据二次根式中的被开方数是非负数列出不等式,解不等式即可.
【解答】解:由题意得,2a﹣1≥0,
解得,a≥,
故答案为:a≥.
【点评】本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.
9.化简:(b>0)=.
【考点】二次根式的性质与化简.
【专题】计算题;二次根式.
【分析】原式利用二次根式性质化简即可得到结果.
【解答】解:原式=,
故答案为:
【点评】此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.
10.某种商品原价100元,经过两次降价后,该种商品的利润减少了36元,那么该商品平均每次降价的百分比是20%.
【考点】一元二次方程的应用.
【专题】增长率问题.
【分析】设每次降价的百分比为x,第 ( http: / / www.21cnjy.com )一次降价后价格变为100(1﹣x),第二次在第一次降价后的基础上再降,变为100(x﹣1)(x﹣1),从而列出方程,求出答案.
【解答】解:设每次降价的百分比为x,根据题意得:
100(x﹣1)2=100﹣36,
解得:x1=1.8,x2=0.2.
因x=1.8不合题意,故舍去,所以x=0.1.
答:该商品平均每次降价的百分比是20%.
故答案为:20%.
【点评】此题考查了一元二次方程的应用,解答本题的关键在于分析降价后的价格,要注意降价的基础,另外还要注意解的取舍.
11.将命题“同角的补角相等”改写成“如果…那么…”形式为如果两个角是同一个角的补角,那么这两个角相等.
【考点】命题与定理.
【分析】“同角的补角相等”的条件是:两个角是同一个角的补角,结论是:这两个角相等.据此即可写成所要求的形式.
【解答】解:“同角的补角相等”的条件是:两个角是同一个角的补角,结论是:这两个角相等.
则将命题“同角的补角相等”改写成“如果…那么…”形式为:如果两个角是同一个角的补角,那么这两个角相等.
故答案是:如果两个角是同一个角的补角,那么这两个角相等.
【点评】本题考查了命题的叙述,正确分清命题的条件和结论是把命题写成“如果…那么…”的形式的关键.
12.若x=﹣1是方程x2﹣mx﹣3=0的一个根,则m的值为2.
【考点】一元二次方程的解.
【分析】把x=﹣1代入已知方程可以得到关于m的一元一次方程,通过解一元一次方程来求m的值.
【解答】解:把x=﹣1代入方程x2﹣mx﹣3=0,得
(﹣1)2﹣(﹣1) m﹣3=0,
解得m=2.
故答案是:2.
【点评】本题考查了一元二次方程的解 ( http: / / www.21cnjy.com )的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.
13.在实数范围内因式分解:x2﹣4x﹣3=(x﹣2+)(x﹣2﹣).
【考点】实数范围内分解因式.
【专题】计算题.
【分析】令原式值为0列出方程,求出方程的解即可得到分解的结果.
【解答】解:令x2﹣4x﹣3=0,
解得:x==2±,
则原式=(x﹣2+)(x﹣2﹣),
故答案为:(x﹣2+)(x﹣2﹣).
【点评】此题考查了实数范围内分解因式,令原式值为0求出x的值是解本题的关键.
14.若|b﹣1|与互为相反数,则(a+b)2015=﹣1.
【考点】非负数的性质:算术平方根;非负数的性质:绝对值.
【分析】根据非负数的性质列出算式,求出a、b的值,根据乘方的意义计算即可.
【解答】解:由题意得,b﹣1=0,a+2=0,
解得,a=﹣2,b=1,
(a+b)2015=﹣1,
故答案为:﹣1.
【点评】本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.
15.如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为120°.
( http: / / www.21cnjy.com )
【考点】等边三角形的性质.
【分析】利用等边三角形的性质以及等腰三角形的性质得出∠B=∠BAD=∠C=∠EAC=30°,进而利用三角形内角和定理求出即可.
【解答】解:∵E是BC的三等分点,且△ADE是等边三角形,
∴BD=DE=EC=AD=AE,∠ADE=∠AED=60°,
∴∠B=∠BAD=∠C=∠EAC=30°,
∴∠BAC=180°﹣∠B﹣∠C=120°.
故答案为:120°.
【点评】此题主要考查了等边三角形的性质与等腰三角形的性质等知识,得出∠B=∠C的度数是解题关键.
16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为75度.
( http: / / www.21cnjy.com )
【考点】三角形内角和定理;平行线的性质.
【专题】计算题.
【分析】根据三角形三内角之和等于180°求解.
【解答】解:如图.
∵∠3=60°,∠4=45°,
∴∠1=∠5=180°﹣∠3﹣∠4=75°.
故答案为:75.
( http: / / www.21cnjy.com )
【点评】考查三角形内角之和等于180°.
17.如图,AB⊥AC,AB=AC=cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=cm.
( http: / / www.21cnjy.com )
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】求出∠BAD=∠ACF=90°,根据 ( http: / / www.21cnjy.com )三角形内角和定理求出∠BAD=∠CAF,根据ASA推出△ABD≌△CDF,根据全等三角形的性质得出AD=CF即可.
【解答】解:∵AB⊥AC,CF∥AB,
∴CF⊥AC,
∴∠BAD=∠ACF=90°,
∵AF⊥BD,
∴∠AEB=∠AED=90°,
∴∠ABD+∠ADB=∠CAF+∠ADB=90°,
∴∠BAD=∠CAF,
在△ABD和△CAF中,
,
∴△ABD≌△CDF(ASA),
∴AD=CF,
∵AC=cm,D为AC中点,
∴AD=AC=,
∴CF=,
故答案为:.
【点评】本题考查了全等三角 ( http: / / www.21cnjy.com )形的性质和判定,平行线的性质,三角形内角和定理的应用,能推出△ABD≌△CDF是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.
18.已知等腰△ABC, ( http: / / www.21cnjy.com )AB=AC,∠C=30°,如果将△ABC绕着点B旋转,使点C正好落在直线AB上的点C′处,那么∠BC′C=15或75度.
【考点】旋转的性质.
【分析】分成顺指针和逆时针两种情况进行讨论,利用等腰三角形的性质:等边对等角以及三角形内角和定理求解.
【解答】解:当顺时针旋转时,C落在C'1的位置,
∵B'1C=BC,
∴∠BC'1C=∠BCC'1,
又∵∠ABC=∠BC'1C+∠BCC'1=30°,
∴∠BC'1C=15°;
当逆时针旋转时,C落在C'2的位置,
∵BC'2=BC,
则∠BC'2C=∠BCC'2===75°.
故答案是:15或75.
( http: / / www.21cnjy.com )
【点评】本题考查了旋转的性质以及等腰三角形的性质,注意到分两种情况进行讨论是本题的关键.
三、简答题(每小题7分,共56分)
19.计算:.
【考点】二次根式的加减法.
【分析】分母有理化的同时,运用二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.
【解答】解:原式=2(+1)+3﹣2
=2+2+3﹣2
=2+3.
【点评】同类二次根式是指几个二次根式化简成最简二次根式后,被开方数相同的二次根式.
合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.
20.解方程:(x+3)(x﹣1)﹣5=0.
【考点】解一元二次方程-因式分解法.
【分析】整理后分解因式,即可得出两个一元一次方程,求出方程的解即可.
【解答】解:整理得:x2+2x﹣8=0,
(x+4)(x﹣2)=0,
x+4=0,x﹣2=0,
x1=﹣4,x2=2,
所以原方程的根是x1=﹣4,x2=2.
【点评】本题考查了解一元二次方程的应用,能把一元二次方程转化成一元一次方程是解此题的关键.
21.解方程:y﹣=﹣.
【考点】解一元二次方程-公式法.
【分析】先去分母,整理后求出b2﹣4ac的值,再代入公式求出即可.
【解答】解 y﹣=﹣,
去分母,得6y﹣3(y2﹣1)=﹣2,
整理,得3y2﹣6y﹣5=0,
b2﹣4ac=(﹣6)2﹣4×3×(﹣5)=96,
y=,
y1=,y2=.
【点评】本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.
22.用配方法解方程:2x2﹣4x+1=0.
【考点】解一元二次方程-配方法.
【专题】配方法.
【分析】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确使用,把左边配成完全平方式,右边化为常数.
【解答】解:原方程化为
配方得
即
开方得
∴,.
【点评】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
23.化简求值:当x=3,y=4时,求代数式+的值.
【考点】二次根式的化简求值.
【分析】首先对第一个式子的分子利用平方 ( http: / / www.21cnjy.com )差公式分解,第二个式子利用完全平方公式分解,然后约分,合并同类二次根式即可化简,然后代入数值计算即可.
【解答】解:原式=+
=+3++
=2+4,
当x=3,y=4时,原式=2+4=2+8.
【点评】本题考查了二次根式的化简求值,正确理解平方差公式和完全平方公式对分子进行变形是关键.
24.已知关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+1=0(m为常数)有两个实数根,求m的取值范围.
【考点】根的判别式.
【分析】根据一元二次方程有两个实数根可知,△>0,列出关于m的不等式,解答即可.
【解答】解:∵关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+1=0有两个实数根,
∴△=b2﹣4ac=[﹣(2m﹣1)]2﹣4(m﹣1)(m+1)=﹣4m+5>0,
又∵(m﹣1)x2﹣(2m﹣1)x+m+1=0是一元二次方程,
∴(m﹣1)≠0,
故m的取值范围是m≤且m≠1.
【点评】此题考查了一元二次方程根的判别式,解题的关键是要明确:
(1)△>0 方程有两个不相等的实数根;
(2)△=0 方程有两个相等的实数根;
(3)△<0 方程没有实数根.
25.如图,要建一个面积为150㎡的长 ( http: / / www.21cnjy.com )方形养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:
(1)求鸡场的长和宽各为多少米?
(2)若将题中条件“墙长为18米” ( http: / / www.21cnjy.com )换为“墙长为a米”,且增加条件“离墙9m开外鸡场一侧准备修条小路”,其他条件不变,则墙长a米至少要多少米?
( http: / / www.21cnjy.com )
【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】(1)设鸡场的宽为x米,平行于墙的边长为35﹣2x米,根据面积为150平方米,可列方程求解.
(2)如果离墙9米开外准备修路,那么宽就要小于9米,可选定墙长为9米,由此进一步分析得出答案即可.
【解答】解:(1)设养鸡场靠墙的边长为x米,则平行于墙的边长为(35﹣2x)米,
由题意得:(35﹣2x)x=150,
即(2x﹣15)(x﹣10)=0,
解得:x=7.5或x=10,
当x=10时,35﹣2x=15<18,符合实际意义;
当x=7.5时,35﹣2x=20>18,不符合实际意义,舍去.
答:养鸡场的长是15米,宽是10米;
(2))求出的平行于墙的一条边应小于墙长a;
如果a大于等于20,则方程有两个解,如果a小于20,大于等于15,则有一个解,如果a小于15,则无解.
根据离墙9米开外准备修路,那么长不小于20米,
即a≥20米,
此时养鸡场的长至少为20米,宽为7.5米.
【点评】本题考查一元二次方程的实际运用,利用长方形的面积得出等量关系建立方程解决问题.
26.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,且AB=CG,AC=BF.
(1)求证:△ABF≌△GCA;
(2)求证:AG⊥AF.
( http: / / www.21cnjy.com )
【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】(1)根据垂直定义得出∠BDC=∠GEC=90°,根据等角的余角相等求出∠ABF=∠ACG,根据全等三角形的判定推出即可;
(2)根据全等三角形的性质得出∠F=∠GAC,求出∠GAC+∠FAE=90°,即可得出答案.
【解答】证明:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠GEC=90°,
∵∠DGB=∠EGC,
∴∠ABF=∠ACG(等角的余角相等),
在△ABF和△GCA中,
,
∴△ABF≌△GCA;
(2)由(1)△ABF≌△GCA,
∴∠F=∠GAC,
∵BE⊥AC,
∴∠AEB=∠F+∠FAE=90°,
∴∠GAC+∠FAE=90°,
∴AG⊥AF.
【点评】本题考查了全等三角形的性质和判定 ( http: / / www.21cnjy.com ),垂直定义的应用,能求出△ABF≌△GCA是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.
四、解答题
27.如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
(1)如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过3秒后,△BPD与△CQP是否全等?请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以(1)②中的运动速度从 ( http: / / www.21cnjy.com )点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
( http: / / www.21cnjy.com )
【考点】全等三角形的判定与性质.
【专题】动点型.
【分析】(1)①先求得BP=CQ=3,PC=BD=5,然后根据等边对等角求得∠B=∠C,最后根据SAS即可证明;
②因为VP≠VQ,所以BP≠CQ,又∠ ( http: / / www.21cnjy.com )B=∠C,要使△BPD与△CQP全等,只能BP=CP=4,根据全等得出CQ=BD=5,然后根据运动速度求得运动时间,根据时间和CQ的长即可求得Q的运动速度;
(2)因为VQ>VP,只能是点Q追上点P,即点Q比点P多走AB+AC的路程,据此列出方程,解这个方程即可求得.
【解答】解:(1)①∵t=3(秒),
∴BP=CQ=3(厘米)
∵AB=10,D为AB中点,
∴BD=5(厘米)
又∵PC=BC﹣BP=8﹣3=5(厘米)
∴PC=BD
∵AB=AC,
∴∠B=∠C,
在△BPD与△CQP中,
,
∴△BPD≌△CQP(SAS),
②∵VP≠VQ,
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4,
∵△BPD≌△CPQ,
∴CQ=BD=5.
∴点P的运动时间t==4(秒),
此时VQ==1.25(厘米/秒).
(2)因为VQ>VP,只能是点Q追上点P,即点Q比点P多走AB+AC的路程
设经过x秒后P与Q第一次相遇,依题意得1.25x=x+2×10,
解得x=80(秒),
此时P运动了80×1=80(厘米),
又∵△ABC的周长为28厘米,80=28×2+24,
∴点P、Q在AB边上相遇,即经过了80秒,点P与点Q第一次在AB边上相遇.
【点评】本题考查了三角形全等的判定和性质,等腰三角形的性质,以及数形结合思想的运用,解题的根据是熟练掌握三角形全等的判定和性质.
一、选择题
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.的一个有理化因式是( )
A. B. C.+ D.﹣
3.下列方程是一元二次方程的是( )
A.ax2﹣2x+=0(a是已知数) B.3x2+2x﹣4=3x2
C.5x2﹣2x=0 D.=1
4.下列二次根式中与是同类二次根式的是( )
A. B. C. D.
5.下列语句中哪个是命题( )
A.联结A、B两点 B.等角的余角相等吗?
C.对顶角相等 D.代数式(a≥0)叫二次根式
6.如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
( http: / / www.21cnjy.com )
A.∠BAC=36°
B.BD平分∠ABC
C.若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54°
D.点N是BD的中点
二、填空题(每小题2分,共24分)
7.计算:﹣=__________.
8.如果有意义,那么a的取值范围是__________.
9.化简:(b>0)=__________.
10.某种商品原价100元,经过两次降价后,该种商品的利润减少了36元,那么该商品平均每次降价的百分比是__________.
11.将命题“同角的补角相等”改写成“如果…那么…”形式为__________.
12.若x=﹣1是方程x2﹣mx﹣3=0的一个根,则m的值为__________.
13.在实数范围内因式分解:x2﹣4x﹣3=__________.
14.若|b﹣1|与互为相反数,则(a+b)2015=__________.
15.如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为__________.
( http: / / www.21cnjy.com )
16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为__________度.
( http: / / www.21cnjy.com )
17.如图,AB⊥AC,AB=AC=cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=__________cm.
( http: / / www.21cnjy.com )
18.已知等腰△ABC,AB=AC,∠C ( http: / / www.21cnjy.com )=30°,如果将△ABC绕着点B旋转,使点C正好落在直线AB上的点C′处,那么∠BC′C=__________度.
三、简答题(每小题7分,共56分)
19.计算:.
20.解方程:(x+3)(x﹣1)﹣5=0.
21.解方程:y﹣=﹣.
22.用配方法解方程:2x2﹣4x+1=0.
23.化简求值:当x=3,y=4时,求代数式+的值.
24.已知关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+1=0(m为常数)有两个实数根,求m的取值范围.
25.如图,要建一个面积为150㎡的长方形 ( http: / / www.21cnjy.com )养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:
(1)求鸡场的长和宽各为多少米?
(2)若将题中条件“墙长为18米”换为“墙 ( http: / / www.21cnjy.com )长为a米”,且增加条件“离墙9m开外鸡场一侧准备修条小路”,其他条件不变,则墙长a米至少要多少米?
( http: / / www.21cnjy.com )
26.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,且AB=CG,AC=BF.
(1)求证:△ABF≌△GCA;
(2)求证:AG⊥AF.
( http: / / www.21cnjy.com )
四、解答题
27.如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
(1)如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过3秒后,△BPD与△CQP是否全等?请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以(1)②中的 ( http: / / www.21cnjy.com )运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
( http: / / www.21cnjy.com )
2015-2016学年上海市黄浦区八年级(上)期中数学试卷
一、选择题
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
【考点】最简二次根式.
【专题】计算题;二次根式.
【分析】利用最简二次根式的定义判断即可.
【解答】解:A、是最简二次根式,正确;
B、=2,错误;
C、=|a|b2,错误;
D、=,错误,
故选A
【点评】此题考查了最简二次根式,熟练掌握最简二次根式的定义是解本题的关键.
2.的一个有理化因式是( )
A. B. C.+ D.﹣
【考点】分母有理化.
【专题】计算题;二次根式.
【分析】找出原式的一个有理化因式即可.
【解答】解:的一个有理化因式是,
故选B
【点评】此题考查了分母有理化,熟练掌握有理化因式的取法是解本题的关键.
3.下列方程是一元二次方程的是( )
A.ax2﹣2x+=0(a是已知数) B.3x2+2x﹣4=3x2
C.5x2﹣2x=0 D. ( http: / / www.21cnjy.com )=1
【考点】一元二次方程的定义.
【专题】计算题;一元二次方程及应用.
【分析】利用一元二次方程的定义判断即可.
【解答】解:5x2﹣2x=0是一元二次方程,
故选C
【点评】此题考查了一元二次方程的定义,熟练掌握一元二次方程的定义是解本题的关键.
4.下列二次根式中与是同类二次根式的是( )
A. B. C. D.
【考点】同类二次根式.
【专题】计算题.
【分析】根据化简成最简二次根式,被开方数相同的二次根式是同类二次根式,可得答案.
【解答】解:,
A、,故A不正确;
B、被开方数不同,故B不正确;
C、,故C正确;
D、,故D不正确;
故选:C.
【点评】本题考查了同类二次根式,先化成最简二次根式,再比较被开方数.
5.下列语句中哪个是命题( )
A.联结A、B两点 B.等角的余角相等吗?
C.对顶角相等 D.代数式(a≥0)叫二次根式
【考点】命题与定理.
【分析】判断一件事情的语句,叫做命题.根据命题的定义进行判断.
【解答】解:A、不能判断其真假,不构成命题,故本选项错误;
B、不能判断其真假,不构成命题,故本选项错误;
C、是,因为能够判断真假,故本选项正确;
D、代数式(a≥0)叫二次根式,是定义,不是命题,故本选项错误.
故选C.
【点评】本题主要考查了命题的定义:判断一件事情的语句是命题,一般有“是”,“不是”等判断词,比较简单.
6.如图,已知AB=AC,AD=BD=BC,那么下列结论中,错误的是( )
( http: / / www.21cnjy.com )
A.∠BAC=36°
B.BD平分∠ABC
C.若取BC边上的中点M,联结AM交BD于N,那么∠MNB=54°
D.点N是BD的中点
【考点】等腰三角形的性质.
【分析】根据等腰三角形的性质得到∠AB ( http: / / www.21cnjy.com )C=∠C=∠BDC,∠BAC=∠ABD,由三角形的外角的性质得到∠BDC=∠BAC+∠ABD=2∠BAC,
推出∠ABC=∠C=2∠BAC,根据三角形的内角和列方程即可得到∠BAC=36°,故A正确;由∠ABD=∠BAC=36°,∠ABC==72°,即可得到BD平分∠ABC,故B正确;根据直角三角形的性质和等腰三角形的性质即可得到∠BNM=54°,故C正确;根据三角形的中位线的性质即可判断D错误,
【解答】解:∵AB=AC,AD=BD=BC,
∴∠ABC=∠C=∠BDC,∠BAC=∠ABD,
∵∠BDC=∠BAC+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∴∠BAC+∠ACB+∠ABC=∠BAC+2∠BAC+2∠BAC=180°,
∴∠BAC=36°,故A正确;
∴∠ABD=∠BAC=36°,
∠ABC==72°,
∴∠ABC=2∠ABD,
∴BD平分∠ABC,故B正确;
∵AB=AC,BM=CM,
∴AM⊥BC,
∴∠AMB=90°,
∵∠DBC=36°,
∴∠BNM=54°,故C正确;
∵AM不平行于AC,BM=CM,
∴BN≠DN,
∴D错误,
故选D.
【点评】本题考查了等腰三角形的性质,角平分线的定义,三角形的内角和,熟练掌握等腰三角形的性质是解题的关键.
二、填空题(每小题2分,共24分)
7.计算:﹣=.
【考点】二次根式的加减法.
【专题】计算题;二次根式.
【分析】原式各项化简后,合并即可得到结果.
【解答】解:原式=4﹣3=,
故答案为:
【点评】此题考查了二次根式的加减法,熟练掌握运算法则是解本题的关键.
8.如果有意义,那么a的取值范围是a≥.
【考点】二次根式有意义的条件.
【分析】根据二次根式中的被开方数是非负数列出不等式,解不等式即可.
【解答】解:由题意得,2a﹣1≥0,
解得,a≥,
故答案为:a≥.
【点评】本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.
9.化简:(b>0)=.
【考点】二次根式的性质与化简.
【专题】计算题;二次根式.
【分析】原式利用二次根式性质化简即可得到结果.
【解答】解:原式=,
故答案为:
【点评】此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.
10.某种商品原价100元,经过两次降价后,该种商品的利润减少了36元,那么该商品平均每次降价的百分比是20%.
【考点】一元二次方程的应用.
【专题】增长率问题.
【分析】设每次降价的百分比为x,第 ( http: / / www.21cnjy.com )一次降价后价格变为100(1﹣x),第二次在第一次降价后的基础上再降,变为100(x﹣1)(x﹣1),从而列出方程,求出答案.
【解答】解:设每次降价的百分比为x,根据题意得:
100(x﹣1)2=100﹣36,
解得:x1=1.8,x2=0.2.
因x=1.8不合题意,故舍去,所以x=0.1.
答:该商品平均每次降价的百分比是20%.
故答案为:20%.
【点评】此题考查了一元二次方程的应用,解答本题的关键在于分析降价后的价格,要注意降价的基础,另外还要注意解的取舍.
11.将命题“同角的补角相等”改写成“如果…那么…”形式为如果两个角是同一个角的补角,那么这两个角相等.
【考点】命题与定理.
【分析】“同角的补角相等”的条件是:两个角是同一个角的补角,结论是:这两个角相等.据此即可写成所要求的形式.
【解答】解:“同角的补角相等”的条件是:两个角是同一个角的补角,结论是:这两个角相等.
则将命题“同角的补角相等”改写成“如果…那么…”形式为:如果两个角是同一个角的补角,那么这两个角相等.
故答案是:如果两个角是同一个角的补角,那么这两个角相等.
【点评】本题考查了命题的叙述,正确分清命题的条件和结论是把命题写成“如果…那么…”的形式的关键.
12.若x=﹣1是方程x2﹣mx﹣3=0的一个根,则m的值为2.
【考点】一元二次方程的解.
【分析】把x=﹣1代入已知方程可以得到关于m的一元一次方程,通过解一元一次方程来求m的值.
【解答】解:把x=﹣1代入方程x2﹣mx﹣3=0,得
(﹣1)2﹣(﹣1) m﹣3=0,
解得m=2.
故答案是:2.
【点评】本题考查了一元二次方程的解 ( http: / / www.21cnjy.com )的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.
13.在实数范围内因式分解:x2﹣4x﹣3=(x﹣2+)(x﹣2﹣).
【考点】实数范围内分解因式.
【专题】计算题.
【分析】令原式值为0列出方程,求出方程的解即可得到分解的结果.
【解答】解:令x2﹣4x﹣3=0,
解得:x==2±,
则原式=(x﹣2+)(x﹣2﹣),
故答案为:(x﹣2+)(x﹣2﹣).
【点评】此题考查了实数范围内分解因式,令原式值为0求出x的值是解本题的关键.
14.若|b﹣1|与互为相反数,则(a+b)2015=﹣1.
【考点】非负数的性质:算术平方根;非负数的性质:绝对值.
【分析】根据非负数的性质列出算式,求出a、b的值,根据乘方的意义计算即可.
【解答】解:由题意得,b﹣1=0,a+2=0,
解得,a=﹣2,b=1,
(a+b)2015=﹣1,
故答案为:﹣1.
【点评】本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.
15.如图,已知点D,E是BC上的三等分点,△ADE是等边三角形,那么∠BAC的度数为120°.
( http: / / www.21cnjy.com )
【考点】等边三角形的性质.
【分析】利用等边三角形的性质以及等腰三角形的性质得出∠B=∠BAD=∠C=∠EAC=30°,进而利用三角形内角和定理求出即可.
【解答】解:∵E是BC的三等分点,且△ADE是等边三角形,
∴BD=DE=EC=AD=AE,∠ADE=∠AED=60°,
∴∠B=∠BAD=∠C=∠EAC=30°,
∴∠BAC=180°﹣∠B﹣∠C=120°.
故答案为:120°.
【点评】此题主要考查了等边三角形的性质与等腰三角形的性质等知识,得出∠B=∠C的度数是解题关键.
16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为75度.
( http: / / www.21cnjy.com )
【考点】三角形内角和定理;平行线的性质.
【专题】计算题.
【分析】根据三角形三内角之和等于180°求解.
【解答】解:如图.
∵∠3=60°,∠4=45°,
∴∠1=∠5=180°﹣∠3﹣∠4=75°.
故答案为:75.
( http: / / www.21cnjy.com )
【点评】考查三角形内角之和等于180°.
17.如图,AB⊥AC,AB=AC=cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=cm.
( http: / / www.21cnjy.com )
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】求出∠BAD=∠ACF=90°,根据 ( http: / / www.21cnjy.com )三角形内角和定理求出∠BAD=∠CAF,根据ASA推出△ABD≌△CDF,根据全等三角形的性质得出AD=CF即可.
【解答】解:∵AB⊥AC,CF∥AB,
∴CF⊥AC,
∴∠BAD=∠ACF=90°,
∵AF⊥BD,
∴∠AEB=∠AED=90°,
∴∠ABD+∠ADB=∠CAF+∠ADB=90°,
∴∠BAD=∠CAF,
在△ABD和△CAF中,
,
∴△ABD≌△CDF(ASA),
∴AD=CF,
∵AC=cm,D为AC中点,
∴AD=AC=,
∴CF=,
故答案为:.
【点评】本题考查了全等三角 ( http: / / www.21cnjy.com )形的性质和判定,平行线的性质,三角形内角和定理的应用,能推出△ABD≌△CDF是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.
18.已知等腰△ABC, ( http: / / www.21cnjy.com )AB=AC,∠C=30°,如果将△ABC绕着点B旋转,使点C正好落在直线AB上的点C′处,那么∠BC′C=15或75度.
【考点】旋转的性质.
【分析】分成顺指针和逆时针两种情况进行讨论,利用等腰三角形的性质:等边对等角以及三角形内角和定理求解.
【解答】解:当顺时针旋转时,C落在C'1的位置,
∵B'1C=BC,
∴∠BC'1C=∠BCC'1,
又∵∠ABC=∠BC'1C+∠BCC'1=30°,
∴∠BC'1C=15°;
当逆时针旋转时,C落在C'2的位置,
∵BC'2=BC,
则∠BC'2C=∠BCC'2===75°.
故答案是:15或75.
( http: / / www.21cnjy.com )
【点评】本题考查了旋转的性质以及等腰三角形的性质,注意到分两种情况进行讨论是本题的关键.
三、简答题(每小题7分,共56分)
19.计算:.
【考点】二次根式的加减法.
【分析】分母有理化的同时,运用二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.
【解答】解:原式=2(+1)+3﹣2
=2+2+3﹣2
=2+3.
【点评】同类二次根式是指几个二次根式化简成最简二次根式后,被开方数相同的二次根式.
合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.
20.解方程:(x+3)(x﹣1)﹣5=0.
【考点】解一元二次方程-因式分解法.
【分析】整理后分解因式,即可得出两个一元一次方程,求出方程的解即可.
【解答】解:整理得:x2+2x﹣8=0,
(x+4)(x﹣2)=0,
x+4=0,x﹣2=0,
x1=﹣4,x2=2,
所以原方程的根是x1=﹣4,x2=2.
【点评】本题考查了解一元二次方程的应用,能把一元二次方程转化成一元一次方程是解此题的关键.
21.解方程:y﹣=﹣.
【考点】解一元二次方程-公式法.
【分析】先去分母,整理后求出b2﹣4ac的值,再代入公式求出即可.
【解答】解 y﹣=﹣,
去分母,得6y﹣3(y2﹣1)=﹣2,
整理,得3y2﹣6y﹣5=0,
b2﹣4ac=(﹣6)2﹣4×3×(﹣5)=96,
y=,
y1=,y2=.
【点评】本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.
22.用配方法解方程:2x2﹣4x+1=0.
【考点】解一元二次方程-配方法.
【专题】配方法.
【分析】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确使用,把左边配成完全平方式,右边化为常数.
【解答】解:原方程化为
配方得
即
开方得
∴,.
【点评】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
23.化简求值:当x=3,y=4时,求代数式+的值.
【考点】二次根式的化简求值.
【分析】首先对第一个式子的分子利用平方 ( http: / / www.21cnjy.com )差公式分解,第二个式子利用完全平方公式分解,然后约分,合并同类二次根式即可化简,然后代入数值计算即可.
【解答】解:原式=+
=+3++
=2+4,
当x=3,y=4时,原式=2+4=2+8.
【点评】本题考查了二次根式的化简求值,正确理解平方差公式和完全平方公式对分子进行变形是关键.
24.已知关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+1=0(m为常数)有两个实数根,求m的取值范围.
【考点】根的判别式.
【分析】根据一元二次方程有两个实数根可知,△>0,列出关于m的不等式,解答即可.
【解答】解:∵关于x的一元二次方程(m﹣1)x2﹣(2m﹣1)x+m+1=0有两个实数根,
∴△=b2﹣4ac=[﹣(2m﹣1)]2﹣4(m﹣1)(m+1)=﹣4m+5>0,
又∵(m﹣1)x2﹣(2m﹣1)x+m+1=0是一元二次方程,
∴(m﹣1)≠0,
故m的取值范围是m≤且m≠1.
【点评】此题考查了一元二次方程根的判别式,解题的关键是要明确:
(1)△>0 方程有两个不相等的实数根;
(2)△=0 方程有两个相等的实数根;
(3)△<0 方程没有实数根.
25.如图,要建一个面积为150㎡的长 ( http: / / www.21cnjy.com )方形养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:
(1)求鸡场的长和宽各为多少米?
(2)若将题中条件“墙长为18米” ( http: / / www.21cnjy.com )换为“墙长为a米”,且增加条件“离墙9m开外鸡场一侧准备修条小路”,其他条件不变,则墙长a米至少要多少米?
( http: / / www.21cnjy.com )
【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】(1)设鸡场的宽为x米,平行于墙的边长为35﹣2x米,根据面积为150平方米,可列方程求解.
(2)如果离墙9米开外准备修路,那么宽就要小于9米,可选定墙长为9米,由此进一步分析得出答案即可.
【解答】解:(1)设养鸡场靠墙的边长为x米,则平行于墙的边长为(35﹣2x)米,
由题意得:(35﹣2x)x=150,
即(2x﹣15)(x﹣10)=0,
解得:x=7.5或x=10,
当x=10时,35﹣2x=15<18,符合实际意义;
当x=7.5时,35﹣2x=20>18,不符合实际意义,舍去.
答:养鸡场的长是15米,宽是10米;
(2))求出的平行于墙的一条边应小于墙长a;
如果a大于等于20,则方程有两个解,如果a小于20,大于等于15,则有一个解,如果a小于15,则无解.
根据离墙9米开外准备修路,那么长不小于20米,
即a≥20米,
此时养鸡场的长至少为20米,宽为7.5米.
【点评】本题考查一元二次方程的实际运用,利用长方形的面积得出等量关系建立方程解决问题.
26.如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,且AB=CG,AC=BF.
(1)求证:△ABF≌△GCA;
(2)求证:AG⊥AF.
( http: / / www.21cnjy.com )
【考点】全等三角形的判定与性质.
【专题】证明题.
【分析】(1)根据垂直定义得出∠BDC=∠GEC=90°,根据等角的余角相等求出∠ABF=∠ACG,根据全等三角形的判定推出即可;
(2)根据全等三角形的性质得出∠F=∠GAC,求出∠GAC+∠FAE=90°,即可得出答案.
【解答】证明:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠GEC=90°,
∵∠DGB=∠EGC,
∴∠ABF=∠ACG(等角的余角相等),
在△ABF和△GCA中,
,
∴△ABF≌△GCA;
(2)由(1)△ABF≌△GCA,
∴∠F=∠GAC,
∵BE⊥AC,
∴∠AEB=∠F+∠FAE=90°,
∴∠GAC+∠FAE=90°,
∴AG⊥AF.
【点评】本题考查了全等三角形的性质和判定 ( http: / / www.21cnjy.com ),垂直定义的应用,能求出△ABF≌△GCA是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.
四、解答题
27.如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
(1)如果点P在线段BC上以1厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过3秒后,△BPD与△CQP是否全等?请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以(1)②中的运动速度从 ( http: / / www.21cnjy.com )点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
( http: / / www.21cnjy.com )
【考点】全等三角形的判定与性质.
【专题】动点型.
【分析】(1)①先求得BP=CQ=3,PC=BD=5,然后根据等边对等角求得∠B=∠C,最后根据SAS即可证明;
②因为VP≠VQ,所以BP≠CQ,又∠ ( http: / / www.21cnjy.com )B=∠C,要使△BPD与△CQP全等,只能BP=CP=4,根据全等得出CQ=BD=5,然后根据运动速度求得运动时间,根据时间和CQ的长即可求得Q的运动速度;
(2)因为VQ>VP,只能是点Q追上点P,即点Q比点P多走AB+AC的路程,据此列出方程,解这个方程即可求得.
【解答】解:(1)①∵t=3(秒),
∴BP=CQ=3(厘米)
∵AB=10,D为AB中点,
∴BD=5(厘米)
又∵PC=BC﹣BP=8﹣3=5(厘米)
∴PC=BD
∵AB=AC,
∴∠B=∠C,
在△BPD与△CQP中,
,
∴△BPD≌△CQP(SAS),
②∵VP≠VQ,
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4,
∵△BPD≌△CPQ,
∴CQ=BD=5.
∴点P的运动时间t==4(秒),
此时VQ==1.25(厘米/秒).
(2)因为VQ>VP,只能是点Q追上点P,即点Q比点P多走AB+AC的路程
设经过x秒后P与Q第一次相遇,依题意得1.25x=x+2×10,
解得x=80(秒),
此时P运动了80×1=80(厘米),
又∵△ABC的周长为28厘米,80=28×2+24,
∴点P、Q在AB边上相遇,即经过了80秒,点P与点Q第一次在AB边上相遇.
【点评】本题考查了三角形全等的判定和性质,等腰三角形的性质,以及数形结合思想的运用,解题的根据是熟练掌握三角形全等的判定和性质.
同课章节目录
