五年级上册数学人教版第四单元《掷一掷》课件(16张PPT)
文档属性
| 名称 | 五年级上册数学人教版第四单元《掷一掷》课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 218.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 15:01:47 | ||
图片预览



文档简介
综合实践
(掷一掷)
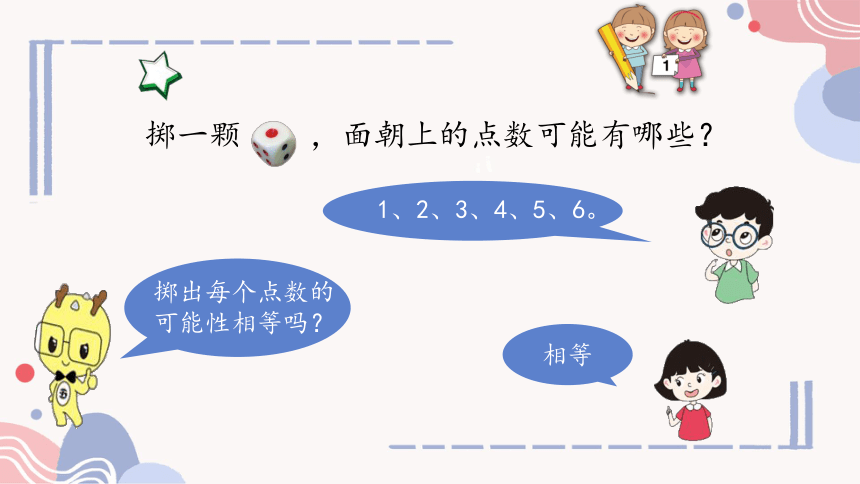
相等
掷一颗
,面朝上的点数可能有哪些?
掷出每个点数的
可能性相等吗?
1、2、3、4、5、6。
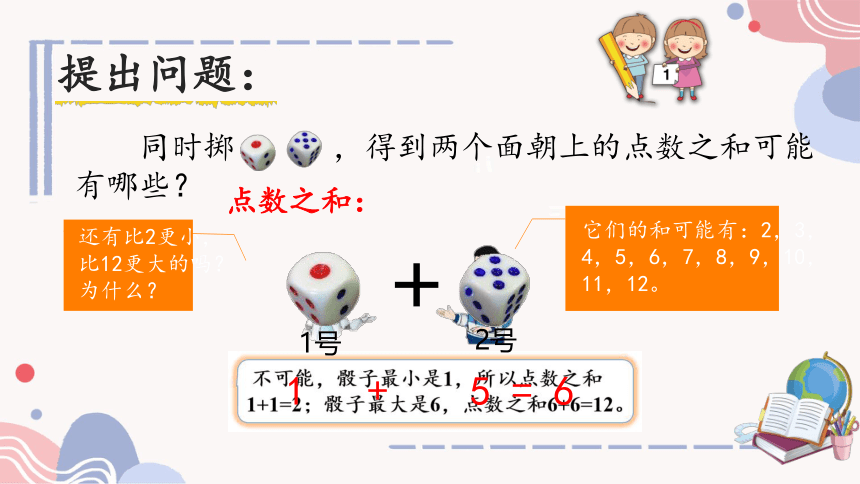
提出问题:
同时掷 ,得到两个面朝上的点数之和可能
有哪些?
它们的和可能有:2,3,
4,5,6,7,8,9,10,
11,12。
还有比2更小,
比12更大的吗?
为什么?
+
点数之和:
1号
2号
1 + 5 = 6
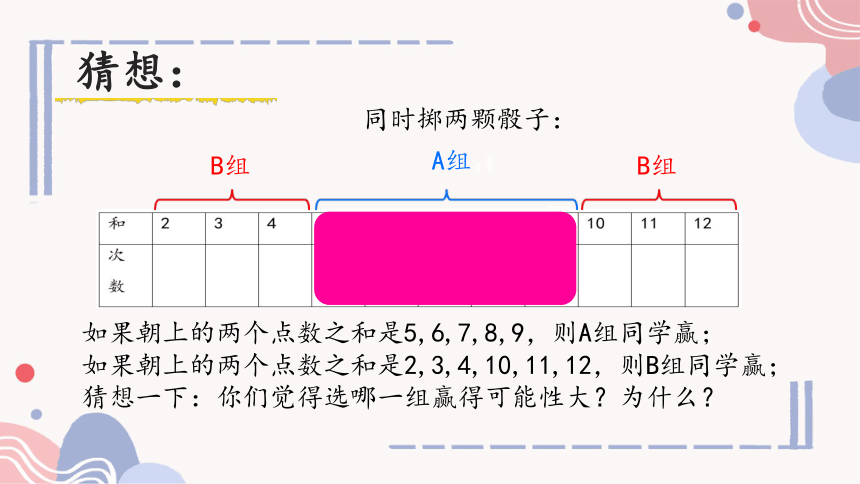
同时掷两颗骰子:
猜想:
B组
B组
A组
如果朝上的两个点数之和是5,6,7,8,9,则A组同学赢;
如果朝上的两个点数之和是2,3,4,10,11,12,则B组同学赢;
猜想一下:你们觉得选哪一组赢得可能性大?为什么?
试验次数少,存在一定的偶然性
小结:
活动一
活动要求:
1.掷一掷:1号,2号各拿2颗骰子,轮流掷。
2.写一写:3号报点数之和,4号记录。和是几,
就在学习单上的几用彩笔涂上一格,涂满其中任意
一列,游戏结束。
3.说一说:观察表格,组内交流写下自己的发现。
活动二
思考:7的点数之和是怎么掷出来的?
验证:
活动要求:
1.写一写:用列举法填写表格。
2.说一说:小组内讨论交流,探究可能性大的本质原因。
分析:
1+2+3=6(种)
4+5+6+5+4=24(种)
3+2+1=6(种)
A组有几种点数之和,B组呢?他们一共有几种?
1+6
2+5
3+4
4+3
5+2
6+1
1+3
2+2
3+1
3+6
4+5
6+3
5+4
1+5
2+4
3+3
4+2
5+1
1+4
2+3
3+2
4+1
2+6
3+5
4+4
5+3
6+2
4+6
5+5
6+4
5+6
6+5
1+2
2+1
1+1
6+6
判断:如果一起掷 ,得到两个数,它们的和出现2,3,4,5,6,7,8,9,10,11,12的可能性相等吗?
分析:
1+6
2+5
3+4
4+3
5+2
6+1
1+3
2+2
3+1
3+6
4+5
6+3
5+4
1+5
2+4
3+3
4+2
5+1
1+4
2+3
3+2
4+1
2+6
3+5
4+4
5+3
6+2
4+6
5+5
6+4
5+6
6+5
1+2
2+1
1+2+3=6(种)
4+5+6+5+4=24(种)
3+2+1=6(种)
1+1
应用:
为了公平比赛,11个和怎样分组更合理呢?
如果继续玩“掷骰子”游戏,怎样的分组更合理呢?
四人小组讨论一下,然后把你们组的设计方案写记录下来。
把“2,3,4,5,6,7,8,9,10,11,12”这11个和重新分组,你们的方案如下:
A组分别有: (共有 种 )
B组分别有: (共有 种 )
重新分组归类:
双数:2,4,6,8,10,12
单数:3,5,7,9,11,
2
1
1
4
1
3
2
2
3
1
6
1
5
2
4
3
3
4
2
5
1
8
2
6
3
5
4
4
5
3
2
6
10
4
6
5
5
4
6
12
6
6
3
1
2
2
1
5
1
4
2
3
3
2
4
1
7
1
6
2
5
3
4
4
3
5
2
6
1
9
3
6
4
5
5
4
6
3
11
5
6
6
5
知识拓展:
超市消费满288元就可以同时掷两颗骰子一次,如果点数之和
是如下几个数字,就可以获得相应的奖品:
东东买完自己需要的东西大约要100元,他要买满288元吗?
让数说话
谈谈你的收获
掷一掷
一个骰子出现面朝上的点数有:1、2、3、4、5、6
两个骰子出现面朝上的点数和有:
2、3、4、5、6、7、8、9、10、11、12
(掷一掷)
相等
掷一颗
,面朝上的点数可能有哪些?
掷出每个点数的
可能性相等吗?
1、2、3、4、5、6。
提出问题:
同时掷 ,得到两个面朝上的点数之和可能
有哪些?
它们的和可能有:2,3,
4,5,6,7,8,9,10,
11,12。
还有比2更小,
比12更大的吗?
为什么?
+
点数之和:
1号
2号
1 + 5 = 6
同时掷两颗骰子:
猜想:
B组
B组
A组
如果朝上的两个点数之和是5,6,7,8,9,则A组同学赢;
如果朝上的两个点数之和是2,3,4,10,11,12,则B组同学赢;
猜想一下:你们觉得选哪一组赢得可能性大?为什么?
试验次数少,存在一定的偶然性
小结:
活动一
活动要求:
1.掷一掷:1号,2号各拿2颗骰子,轮流掷。
2.写一写:3号报点数之和,4号记录。和是几,
就在学习单上的几用彩笔涂上一格,涂满其中任意
一列,游戏结束。
3.说一说:观察表格,组内交流写下自己的发现。
活动二
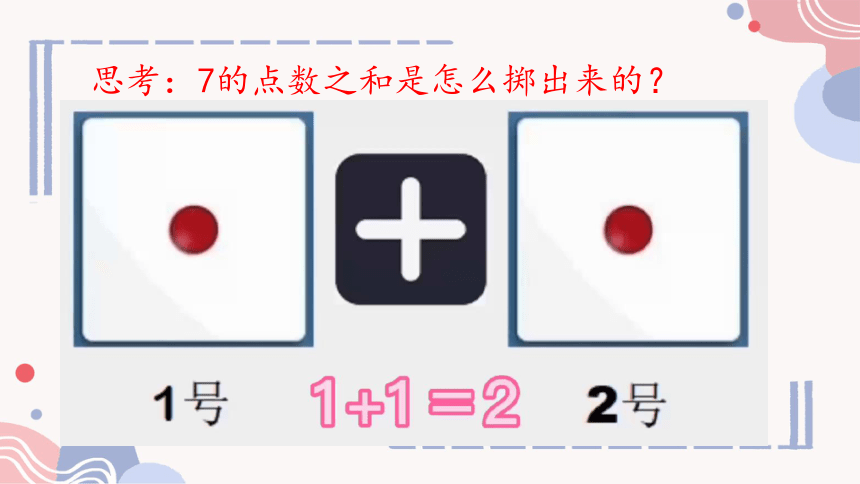
思考:7的点数之和是怎么掷出来的?
验证:
活动要求:
1.写一写:用列举法填写表格。
2.说一说:小组内讨论交流,探究可能性大的本质原因。
分析:
1+2+3=6(种)
4+5+6+5+4=24(种)
3+2+1=6(种)
A组有几种点数之和,B组呢?他们一共有几种?
1+6
2+5
3+4
4+3
5+2
6+1
1+3
2+2
3+1
3+6
4+5
6+3
5+4
1+5
2+4
3+3
4+2
5+1
1+4
2+3
3+2
4+1
2+6
3+5
4+4
5+3
6+2
4+6
5+5
6+4
5+6
6+5
1+2
2+1
1+1
6+6
判断:如果一起掷 ,得到两个数,它们的和出现2,3,4,5,6,7,8,9,10,11,12的可能性相等吗?
分析:
1+6
2+5
3+4
4+3
5+2
6+1
1+3
2+2
3+1
3+6
4+5
6+3
5+4
1+5
2+4
3+3
4+2
5+1
1+4
2+3
3+2
4+1
2+6
3+5
4+4
5+3
6+2
4+6
5+5
6+4
5+6
6+5
1+2
2+1
1+2+3=6(种)
4+5+6+5+4=24(种)
3+2+1=6(种)
1+1
应用:
为了公平比赛,11个和怎样分组更合理呢?
如果继续玩“掷骰子”游戏,怎样的分组更合理呢?
四人小组讨论一下,然后把你们组的设计方案写记录下来。
把“2,3,4,5,6,7,8,9,10,11,12”这11个和重新分组,你们的方案如下:
A组分别有: (共有 种 )
B组分别有: (共有 种 )
重新分组归类:
双数:2,4,6,8,10,12
单数:3,5,7,9,11,
2
1
1
4
1
3
2
2
3
1
6
1
5
2
4
3
3
4
2
5
1
8
2
6
3
5
4
4
5
3
2
6
10
4
6
5
5
4
6
12
6
6
3
1
2
2
1
5
1
4
2
3
3
2
4
1
7
1
6
2
5
3
4
4
3
5
2
6
1
9
3
6
4
5
5
4
6
3
11
5
6
6
5
知识拓展:
超市消费满288元就可以同时掷两颗骰子一次,如果点数之和
是如下几个数字,就可以获得相应的奖品:
东东买完自己需要的东西大约要100元,他要买满288元吗?
让数说话
谈谈你的收获
掷一掷
一个骰子出现面朝上的点数有:1、2、3、4、5、6
两个骰子出现面朝上的点数和有:
2、3、4、5、6、7、8、9、10、11、12
