浙江省温州中考数学预测卷一(含解析)
文档属性
| 名称 | 浙江省温州中考数学预测卷一(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 598.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 00:00:00 | ||
图片预览



文档简介
浙江省温州中考预测卷一
一、选择题(共10题;共30分)
1.(3分)估算 的值在( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.(3分)对某校901班和902班的学生“最喜爱的球类体育项目”进行统计,分别绘制了扇形统计图(如图),下列说法正确的是( )
A.901班中最喜欢足球的人数比902班中最喜欢足球的人数少
B.901班中最喜欢篮球的人数和902班中最喜欢篮球的人数一样多
C.901班中最喜欢足球的人数比最喜欢篮球的人数多
D.902班中最喜欢篮球的人数和最喜欢足球的人数一样多
3.(3分)使分式有意义的条件是( )
A. B. C. D.
4.(3分)下列立体图形中,左视图是圆的是( )
A. B. C. D.
5.(3分)下列运算正确的是( )
A. B. C. D.
6.(3分)如图,圆内接四边形中,,连接,,,,.则的度数是( )
A. B. C. D.
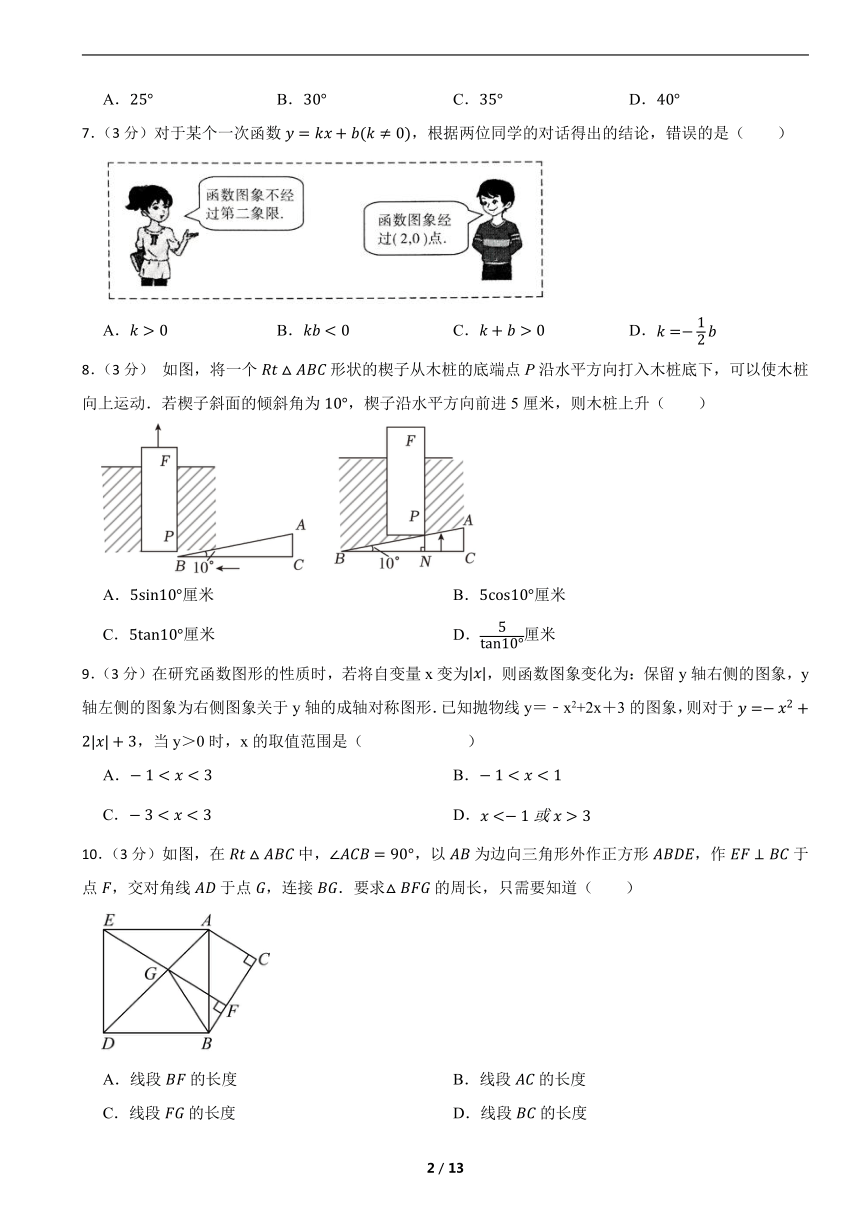
7.(3分)对于某个一次函数,根据两位同学的对话得出的结论,错误的是( )
A. B. C. D.
8.(3分) 如图,将一个形状的楔子从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.若楔子斜面的倾斜角为,楔子沿水平方向前进5厘米,则木桩上升( )
A.厘米 B.厘米
C.厘米 D.厘米
9.(3分)在研究函数图形的性质时,若将自变量x变为,则函数图象变化为:保留y轴右侧的图象,y轴左侧的图象为右侧图象关于y轴的成轴对称图形.已知抛物线y=﹣x2+2x+3的图象,则对于,当y>0时,x的取值范围是( )
A. B.
C. D.
10.(3分)如图,在中,,以为边向三角形外作正方形,作于点,交对角线于点,连接.要求的周长,只需要知道( )
A.线段的长度 B.线段的长度
C.线段的长度 D.线段的长度
二、填空题(共6题;共18分)
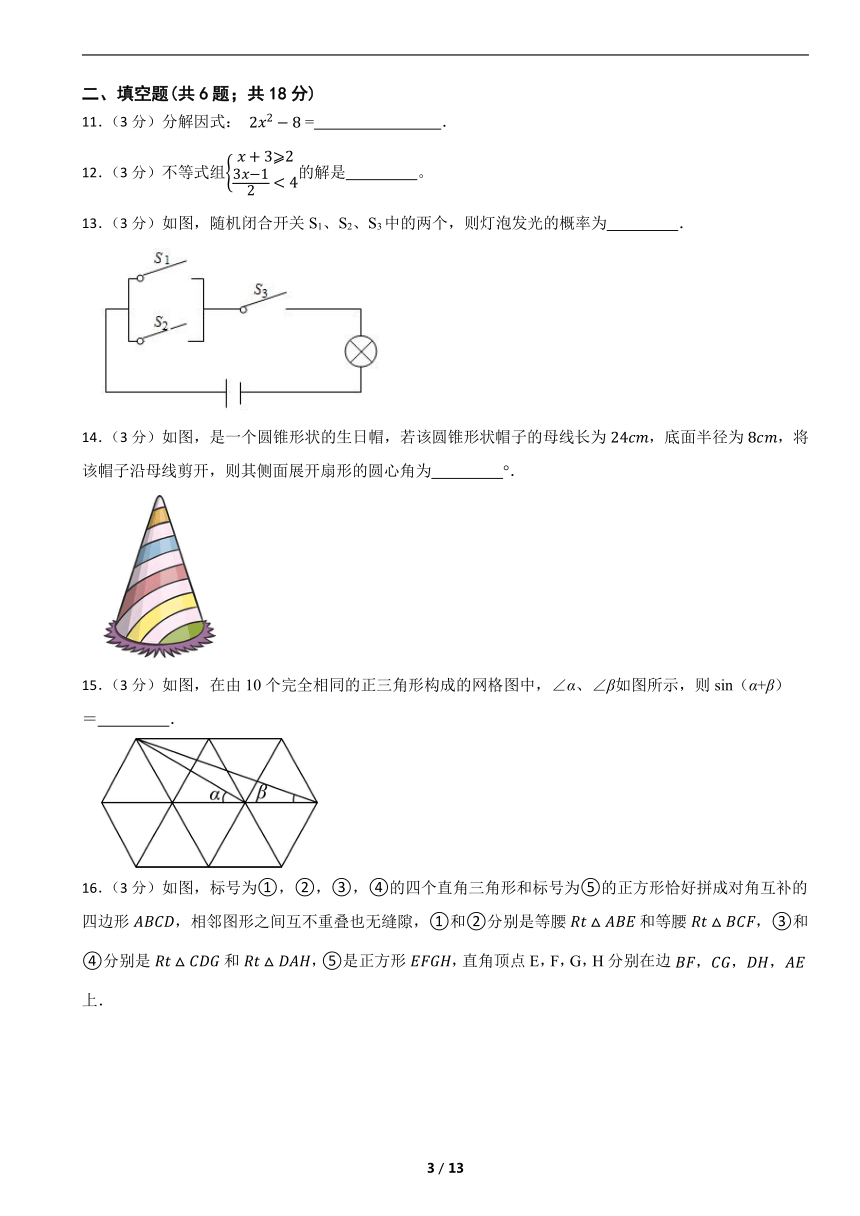
11.(3分)分解因式: = .
12.(3分)不等式组的解是 。
13.(3分)如图,随机闭合开关S1、S2、S3中的两个,则灯泡发光的概率为 .
14.(3分)如图,是一个圆锥形状的生日帽,若该圆锥形状帽子的母线长为,底面半径为,将该帽子沿母线剪开,则其侧面展开扇形的圆心角为 °.
15.(3分)如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则sin(α+β)= .
16.(3分)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形,相邻图形之间互不重叠也无缝隙,①和②分别是等腰和等腰,③和④分别是和,⑤是正方形,直角顶点E,F,G,H分别在边上.
(1)若,,则的长是 cm.
(2)若,则的值是 .
三、计算题(共1题;共8分)
17.(8分)(1)(4分)计算:;
(2)(4分)化简:
四、解答题(共7题;共64分)
18.(8分)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:AF=DE.
19.(8分)我国男性的体质系数计算公式是:,其中W表示体重(单位:),H表示身高(单位:).通过计算出的体质系数m对体质进行评价.具体评价如下表:
m
评价结果 明显消瘦 消瘦 正常 过重 肥胖
(1)(2分)某男生的身高是,体重是,他的体质评价结果是________.
(2)(3分)现从某校九年级学生中随机抽取n名男生进行体质评价,评价结果统计如下:
①抽查的学生数________;图②中a的值为________.
②图①中,体质评价结果为“正常”的扇形圆心角为________°.
(3)(3分)若该校九年级共有男生450人,试估计该校九年级体质评价结果为“过重”或“肥胖”男生人数的和.
20.(8分) 定义:对于任何有理数,符号表示不大于的最大整数.例如:,,.
(1)(4分)填空:= ,= ;
(2)(2分)如果,求满足条件的的取值范围;
(3)(2分)求方程的整数解.
21.(8分)已知反比例函数(k是常数,)与一次函数图象有一个交点的横坐标是.
(1)(2分)求k的值;
(2)(3分)求另一个交点坐标;
(3)(3分)直接写出时x的取值范围.
22.(10分)如图1,正方形的边长是2,E为对角线上一动点,,,当点E从点B运动到点D的过程中,回答下列问题
(1)(3分)求对角线的长度;
(2)(3分)求周长的最小值;
(3)(4分)如图2,在线段上取一点G,连接和,当时,试探究和的数量关系.
23.(10分)定义:平面直角坐标系中,若点,点,且,则称点Q是点P的“k级变换点”.例如,点是的“级变换点”.
(1)(3分)函数的图象上是否存在点的“k级变换点”?若存在,求出k的值,若不存在,说明理由;
(2)(3分)点A为直线:上的一点,它的“k级变换点”B在直线上,直接写出直线的函数表达式.
(3)(4分)若关于x的二次函数的图象上恰有两个点,,这两个点的“1级变换点”都在直线上,并且同时满足:①,②,求的取值范围.
24.(12分)如图,在中,∠B是锐角,,,在射线上取一点P,过P作于点E,过P,E,C三点作.
(1)(4分)当时,
①如图1,若与相切于点P,连结,求的长;
②如图2,若经过点D,求的半径长.
(2)(8分)如图3,已知与射线交于另一点F,将沿所在的直线翻折,点B的对应点记为,且恰好同时落在和边上,求此时的长.
答案解析部分
1.【答案】C
【解析】【解答】解:
,即
则 的值在2和3之间
故答案为:C.
【分析】由题意先找出与5最接近的两个能开得尽方的因数4和9,再求算术平方根可求解.
2.【答案】D
3.【答案】D
【解析】【解答】解:∵分式有意义,
∴,
解得:,
故答案为:D.
【分析】分式有意义的条件:分母不等于零,据此求解.
4.【答案】D
【解析】【解答】A、左视图不是圆,A不符合题意;
B、左视图不是圆,B不符合题意;
C、左视图不是圆,C不符合题意;
D、左视图是圆,D符合题意;
故答案为:D.
【分析】利用三视图的定义求解即可。
5.【答案】B
6.【答案】A
【解析】【解答】解:,
,
,
,,
,
,
故答案为:A.
【分析】本题考查了圆内接四边形的性质和圆周角定理,合理运用定理找到角之间的关系是解题关键.
7.【答案】C
【解析】【解答】解:∵一次函数的图象不经过第二象限,
∴b≤0,
又∵函数图象经过点(2,0),
∴函数图象经过第一、三、四象限,
∴k>0,k=,
∴kb<0,
∴k+b=,
∴错误的是C选项,
故答案为:C.
【分析】根据题意先求出b≤0,再求出函数图象经过第一、三、四象限,最后对每个选项一一判断即可。
8.【答案】C
【解析】【解答】解:∵
∴
故答案为:C.
【分析】根据题意得到:进而在中利用三角函数即可求解.
9.【答案】C
10.【答案】D
11.【答案】
【解析】【解答】根据因式分解的步骤:一提(公因式)二套(公式)三查(是否分解彻底),可知先提公因式,然后根据平方差公式分解即可,即 .
【分析】根据因式分解的步骤:一提(公因式)二套(公式)三查(是否分解彻底),可知先提公因式,然后根据平方差公式分解即可.2 8有公因式2可提取,然后将(-4)用平方差公式分解即可。
12.【答案】
【解析】【解答】解: ,
由①得x≥-1,
由②得x<3,
∴该不等式组的解为:-1≤x<3.
故答案为:-1≤x<3.
【分析】根据解不等式的步骤分别求出不等式组中每一个不等式的解集,进而根据口诀:同大取大,同小取小,大小小大中间找,大大小小无解了,确定出该不等式组的解集.
13.【答案】
【解析】【解答】解:随机闭合开关、、中的两个出现的情况列表得:
开关
结果 不亮 亮 亮
共三种等可能结果,其中正确的有两种
所以能让灯泡发光的概率为,
故答案为:.
【分析】利用列表法求出所有等可能的情况数,再利用概率公式求解即可。
14.【答案】
15.【答案】
【解析】【解答】解:连接DE,如图所示:
在△ABC中,∠ABC=120°,BA=BC,
∴∠α=30°,
同理得:∠CDE=∠CED=30°=∠α.
又∵∠AEC=60°,
∴∠AED=∠AEC+∠CED=90°.
设等边三角形的边长为a,则AE=2a,DE=2×sin60° a=a,
∴AD=a,
∴sin(α+β)= =.
故答案为:.
【分析】连接DE,先求出∠CDE=∠CED=30°=∠α.再求出∠AED=∠AEC+∠CED=90°,设等边三角形的边长为a,则AE=2a,DE=2×sin60° a=a,利用勾股定理求出AD的长,最后利用正弦的定义求出sin(α+β)= =即可.
16.【答案】4;3
17.【答案】(1)解:原式.
(2)解:原式
【解析】【分析】(1)实数的混合运算,先计算非零数的零次幂和负整数指数幂,代入特殊角的三角函数值,再进行加减运算.
(2)分式的化简,需要对括号里面部分进行通分并合并同类项,然后再进行乘法运算.
18.【答案】证明:,
,
,
在和中,
,
,
.
【解析】【分析】由BE=CF可证得BF=CE,利用SAS证明△ABF≌△DCE,利用全等三角形的性质可证得结论.
19.【答案】(1)过重
(2)①60,5;②96
(3)270人
20.【答案】(1)3;2;
(2)解:由题:
解得不等式组的解集为:
(3)解:由题得:
∴
解得不等式组的解集为:
∵是整数
设(是整数)
∴
解得不等式组的解集为:
∵是整数
∴,
∵x是方程的整数解,
∴只有当,方程的整数解为.
【解析】【解答】解:(1) ,
故答案为:3 , 2 ;
【分析】(1)根据题目中所给的运算方法求解即可;
(2)根据题目中所给的运算方法建立不等式组,解不等式组即可求得x的取值范围;
(3)把方程化为,根据题目中所给的运算方法建立不等式组,解不等式组可得x的范围,已知[x]是整数,设4x+5=3n(n是整数),建立n的不等式组,解得不等式组可得整数n的值,分别代入求解即可。
21.【答案】(1)
(2)另一个交点坐标为
(3)或
22.【答案】(1)解:四边形是正方形,,
在中,
(2)解:四边形是正方形,,
,,,
又,,
即是个定值,要使周长最小,就要使长度最小
在中,,
当最小时,取得最小值
连接,交于点O,
在正方形中,,
如图2,当,即点E与点O重合时最小,
此时,
的周长最小值是
(3)解:如图3,在上截取,连接.
在正方形中,,
又,,
由(2)知,
,
又,,,即
又,,
,
23.【答案】(1)存在,
(2)直线:
(3)
24.【答案】(1)①;②的半径长为;
(2).
1 / 1
一、选择题(共10题;共30分)
1.(3分)估算 的值在( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.(3分)对某校901班和902班的学生“最喜爱的球类体育项目”进行统计,分别绘制了扇形统计图(如图),下列说法正确的是( )
A.901班中最喜欢足球的人数比902班中最喜欢足球的人数少
B.901班中最喜欢篮球的人数和902班中最喜欢篮球的人数一样多
C.901班中最喜欢足球的人数比最喜欢篮球的人数多
D.902班中最喜欢篮球的人数和最喜欢足球的人数一样多
3.(3分)使分式有意义的条件是( )
A. B. C. D.
4.(3分)下列立体图形中,左视图是圆的是( )
A. B. C. D.
5.(3分)下列运算正确的是( )
A. B. C. D.
6.(3分)如图,圆内接四边形中,,连接,,,,.则的度数是( )
A. B. C. D.
7.(3分)对于某个一次函数,根据两位同学的对话得出的结论,错误的是( )
A. B. C. D.
8.(3分) 如图,将一个形状的楔子从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.若楔子斜面的倾斜角为,楔子沿水平方向前进5厘米,则木桩上升( )
A.厘米 B.厘米
C.厘米 D.厘米
9.(3分)在研究函数图形的性质时,若将自变量x变为,则函数图象变化为:保留y轴右侧的图象,y轴左侧的图象为右侧图象关于y轴的成轴对称图形.已知抛物线y=﹣x2+2x+3的图象,则对于,当y>0时,x的取值范围是( )
A. B.
C. D.
10.(3分)如图,在中,,以为边向三角形外作正方形,作于点,交对角线于点,连接.要求的周长,只需要知道( )
A.线段的长度 B.线段的长度
C.线段的长度 D.线段的长度
二、填空题(共6题;共18分)
11.(3分)分解因式: = .
12.(3分)不等式组的解是 。
13.(3分)如图,随机闭合开关S1、S2、S3中的两个,则灯泡发光的概率为 .
14.(3分)如图,是一个圆锥形状的生日帽,若该圆锥形状帽子的母线长为,底面半径为,将该帽子沿母线剪开,则其侧面展开扇形的圆心角为 °.
15.(3分)如图,在由10个完全相同的正三角形构成的网格图中,∠α、∠β如图所示,则sin(α+β)= .
16.(3分)如图,标号为①,②,③,④的四个直角三角形和标号为⑤的正方形恰好拼成对角互补的四边形,相邻图形之间互不重叠也无缝隙,①和②分别是等腰和等腰,③和④分别是和,⑤是正方形,直角顶点E,F,G,H分别在边上.
(1)若,,则的长是 cm.
(2)若,则的值是 .
三、计算题(共1题;共8分)
17.(8分)(1)(4分)计算:;
(2)(4分)化简:
四、解答题(共7题;共64分)
18.(8分)如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:AF=DE.
19.(8分)我国男性的体质系数计算公式是:,其中W表示体重(单位:),H表示身高(单位:).通过计算出的体质系数m对体质进行评价.具体评价如下表:
m
评价结果 明显消瘦 消瘦 正常 过重 肥胖
(1)(2分)某男生的身高是,体重是,他的体质评价结果是________.
(2)(3分)现从某校九年级学生中随机抽取n名男生进行体质评价,评价结果统计如下:
①抽查的学生数________;图②中a的值为________.
②图①中,体质评价结果为“正常”的扇形圆心角为________°.
(3)(3分)若该校九年级共有男生450人,试估计该校九年级体质评价结果为“过重”或“肥胖”男生人数的和.
20.(8分) 定义:对于任何有理数,符号表示不大于的最大整数.例如:,,.
(1)(4分)填空:= ,= ;
(2)(2分)如果,求满足条件的的取值范围;
(3)(2分)求方程的整数解.
21.(8分)已知反比例函数(k是常数,)与一次函数图象有一个交点的横坐标是.
(1)(2分)求k的值;
(2)(3分)求另一个交点坐标;
(3)(3分)直接写出时x的取值范围.
22.(10分)如图1,正方形的边长是2,E为对角线上一动点,,,当点E从点B运动到点D的过程中,回答下列问题
(1)(3分)求对角线的长度;
(2)(3分)求周长的最小值;
(3)(4分)如图2,在线段上取一点G,连接和,当时,试探究和的数量关系.
23.(10分)定义:平面直角坐标系中,若点,点,且,则称点Q是点P的“k级变换点”.例如,点是的“级变换点”.
(1)(3分)函数的图象上是否存在点的“k级变换点”?若存在,求出k的值,若不存在,说明理由;
(2)(3分)点A为直线:上的一点,它的“k级变换点”B在直线上,直接写出直线的函数表达式.
(3)(4分)若关于x的二次函数的图象上恰有两个点,,这两个点的“1级变换点”都在直线上,并且同时满足:①,②,求的取值范围.
24.(12分)如图,在中,∠B是锐角,,,在射线上取一点P,过P作于点E,过P,E,C三点作.
(1)(4分)当时,
①如图1,若与相切于点P,连结,求的长;
②如图2,若经过点D,求的半径长.
(2)(8分)如图3,已知与射线交于另一点F,将沿所在的直线翻折,点B的对应点记为,且恰好同时落在和边上,求此时的长.
答案解析部分
1.【答案】C
【解析】【解答】解:
,即
则 的值在2和3之间
故答案为:C.
【分析】由题意先找出与5最接近的两个能开得尽方的因数4和9,再求算术平方根可求解.
2.【答案】D
3.【答案】D
【解析】【解答】解:∵分式有意义,
∴,
解得:,
故答案为:D.
【分析】分式有意义的条件:分母不等于零,据此求解.
4.【答案】D
【解析】【解答】A、左视图不是圆,A不符合题意;
B、左视图不是圆,B不符合题意;
C、左视图不是圆,C不符合题意;
D、左视图是圆,D符合题意;
故答案为:D.
【分析】利用三视图的定义求解即可。
5.【答案】B
6.【答案】A
【解析】【解答】解:,
,
,
,,
,
,
故答案为:A.
【分析】本题考查了圆内接四边形的性质和圆周角定理,合理运用定理找到角之间的关系是解题关键.
7.【答案】C
【解析】【解答】解:∵一次函数的图象不经过第二象限,
∴b≤0,
又∵函数图象经过点(2,0),
∴函数图象经过第一、三、四象限,
∴k>0,k=,
∴kb<0,
∴k+b=,
∴错误的是C选项,
故答案为:C.
【分析】根据题意先求出b≤0,再求出函数图象经过第一、三、四象限,最后对每个选项一一判断即可。
8.【答案】C
【解析】【解答】解:∵
∴
故答案为:C.
【分析】根据题意得到:进而在中利用三角函数即可求解.
9.【答案】C
10.【答案】D
11.【答案】
【解析】【解答】根据因式分解的步骤:一提(公因式)二套(公式)三查(是否分解彻底),可知先提公因式,然后根据平方差公式分解即可,即 .
【分析】根据因式分解的步骤:一提(公因式)二套(公式)三查(是否分解彻底),可知先提公因式,然后根据平方差公式分解即可.2 8有公因式2可提取,然后将(-4)用平方差公式分解即可。
12.【答案】
【解析】【解答】解: ,
由①得x≥-1,
由②得x<3,
∴该不等式组的解为:-1≤x<3.
故答案为:-1≤x<3.
【分析】根据解不等式的步骤分别求出不等式组中每一个不等式的解集,进而根据口诀:同大取大,同小取小,大小小大中间找,大大小小无解了,确定出该不等式组的解集.
13.【答案】
【解析】【解答】解:随机闭合开关、、中的两个出现的情况列表得:
开关
结果 不亮 亮 亮
共三种等可能结果,其中正确的有两种
所以能让灯泡发光的概率为,
故答案为:.
【分析】利用列表法求出所有等可能的情况数,再利用概率公式求解即可。
14.【答案】
15.【答案】
【解析】【解答】解:连接DE,如图所示:
在△ABC中,∠ABC=120°,BA=BC,
∴∠α=30°,
同理得:∠CDE=∠CED=30°=∠α.
又∵∠AEC=60°,
∴∠AED=∠AEC+∠CED=90°.
设等边三角形的边长为a,则AE=2a,DE=2×sin60° a=a,
∴AD=a,
∴sin(α+β)= =.
故答案为:.
【分析】连接DE,先求出∠CDE=∠CED=30°=∠α.再求出∠AED=∠AEC+∠CED=90°,设等边三角形的边长为a,则AE=2a,DE=2×sin60° a=a,利用勾股定理求出AD的长,最后利用正弦的定义求出sin(α+β)= =即可.
16.【答案】4;3
17.【答案】(1)解:原式.
(2)解:原式
【解析】【分析】(1)实数的混合运算,先计算非零数的零次幂和负整数指数幂,代入特殊角的三角函数值,再进行加减运算.
(2)分式的化简,需要对括号里面部分进行通分并合并同类项,然后再进行乘法运算.
18.【答案】证明:,
,
,
在和中,
,
,
.
【解析】【分析】由BE=CF可证得BF=CE,利用SAS证明△ABF≌△DCE,利用全等三角形的性质可证得结论.
19.【答案】(1)过重
(2)①60,5;②96
(3)270人
20.【答案】(1)3;2;
(2)解:由题:
解得不等式组的解集为:
(3)解:由题得:
∴
解得不等式组的解集为:
∵是整数
设(是整数)
∴
解得不等式组的解集为:
∵是整数
∴,
∵x是方程的整数解,
∴只有当,方程的整数解为.
【解析】【解答】解:(1) ,
故答案为:3 , 2 ;
【分析】(1)根据题目中所给的运算方法求解即可;
(2)根据题目中所给的运算方法建立不等式组,解不等式组即可求得x的取值范围;
(3)把方程化为,根据题目中所给的运算方法建立不等式组,解不等式组可得x的范围,已知[x]是整数,设4x+5=3n(n是整数),建立n的不等式组,解得不等式组可得整数n的值,分别代入求解即可。
21.【答案】(1)
(2)另一个交点坐标为
(3)或
22.【答案】(1)解:四边形是正方形,,
在中,
(2)解:四边形是正方形,,
,,,
又,,
即是个定值,要使周长最小,就要使长度最小
在中,,
当最小时,取得最小值
连接,交于点O,
在正方形中,,
如图2,当,即点E与点O重合时最小,
此时,
的周长最小值是
(3)解:如图3,在上截取,连接.
在正方形中,,
又,,
由(2)知,
,
又,,,即
又,,
,
23.【答案】(1)存在,
(2)直线:
(3)
24.【答案】(1)①;②的半径长为;
(2).
1 / 1
同课章节目录
