6.4.4 正弦定理(1)学案(含解析)高中数学人教A版(2019)必修 第二册
文档属性
| 名称 | 6.4.4 正弦定理(1)学案(含解析)高中数学人教A版(2019)必修 第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 17:07:58 | ||
图片预览



文档简介
6.4.4 正弦定理(1)
1. 掌握正弦定理,并能解决一些简单的三角形中边与角的计算.
2. 体会“由特殊到一般”的数学思想方法.
活动一 了解正弦定理的探求过程
探究:余弦定理及其推论分别给出了已知两边及其夹角、已知三边直接解三角形的公式.如果已知两角和一边,是否也有相应的直接解三角形的公式呢?
问题1:如图,在Rt△ABC中,C=90°,边a,b,c与角A,B的关系是什么?
问题2:在Rt△ABC中,==,对于锐角三角形和钝角三角形,这个关系式是否仍然成立?如何证明?
结论:正弦定理:
思考1
你能用其他方法推导出正弦定理吗?
思考2
在正弦定理中,比值==与△ABC的外接圆的直径之间存在怎样的关系?
正弦定理指出了三角形中三条边与对应角的正弦之间的关系,描述了三角形中边与角的一种数量关系.
活动二 掌握正弦定理的简单应用
例1 在△ABC中,已知b=16,A=45°,a=16,求角B,C及边c.
(1) 在例1的条件下,将“a=16”改为“a=16”,结论如何?
(2) 在例1的条件下,将“a=16”改为“a=8”,结论又如何?
解三角形有三种情况,两解,一解,无解.要考虑大角对大边,大边对大角,及正弦定理有a>b sin A>sin B,由此确定解的情况.
在△ABC中,已知B=30°,b=,c=2,解这个三角形.
活动三 掌握正弦定理在实际问题中的应用
例2 在△ABC中,已知A=75°,C=60°,A,C之间的距离b为100m,求A,B之间的距离c.
如图,在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.
思考3
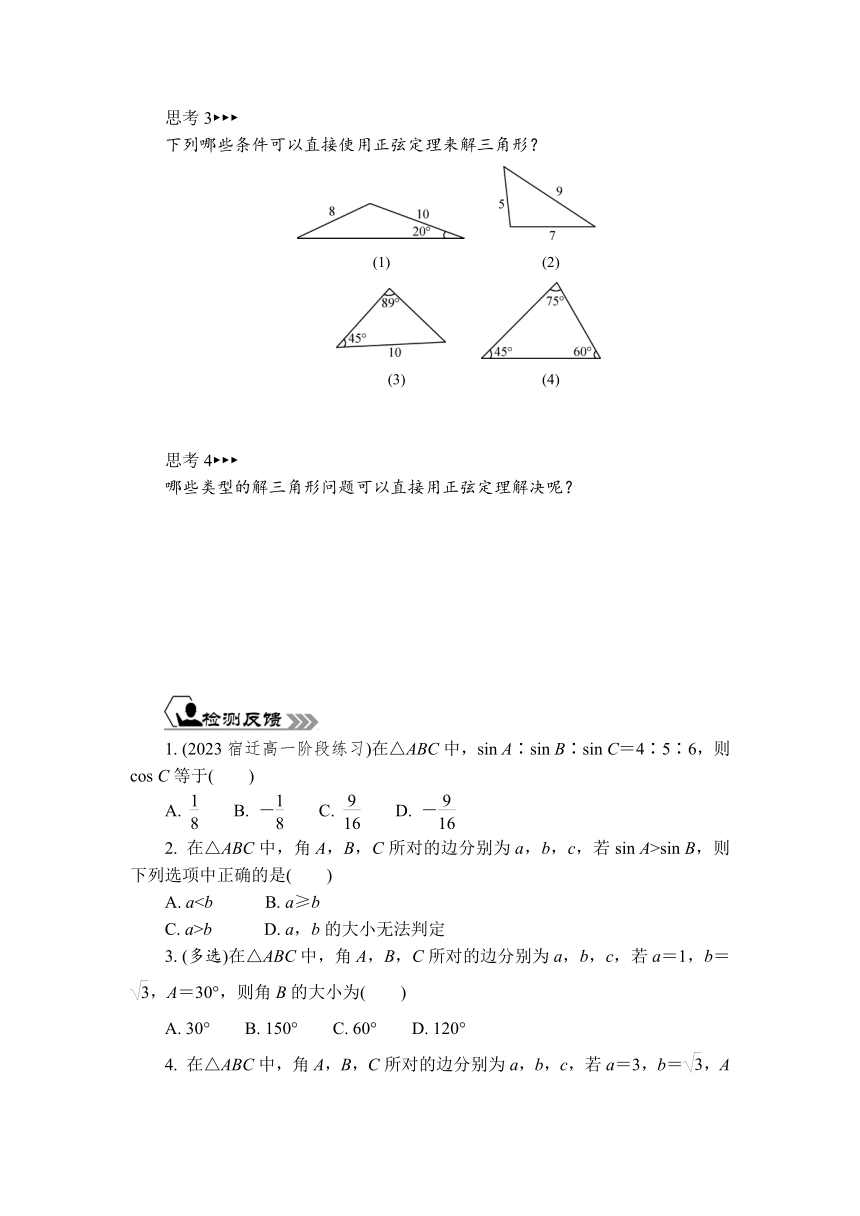
下列哪些条件可以直接使用正弦定理来解三角形?
(2)
(3) (4)
思考4
哪些类型的解三角形问题可以直接用正弦定理解决呢?
1. (2023宿迁高一阶段练习)在△ABC中,sin A∶sin B∶sin C=4∶5∶6,则cos C等于( )
A. B. - C. D. -
2. 在△ABC中,角A,B,C所对的边分别为a,b,c,若sin A>sin B,则下列选项中正确的是( )
A. aC. a>b D. a,b的大小无法判定
3. (多选)在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=,A=30°,则角B的大小为( )
A. 30° B. 150° C. 60° D. 120°
4. 在△ABC中,角A,B,C所对的边分别为a,b,c,若a=3,b=,A=,则角C的大小为________.
5. (2023郑州中牟县第一高级中学高一阶段练习)已知△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,且(b2+c2-a2)=4S.
(1) 求角A的大小;
(2) 若a=,求b+2c的最大值.
【答案解析】
6.4.4 正弦定理(1)
【活动方案】
问题1:sin A=,sin B=.
问题2:成立,证明如下:
在锐角三角形ABC中,过点A作与垂直的单位向量j,则j与的夹角为-A,j与的夹角为-C.
因为+=,
所以j·(+)=j·,
即|j|||cos +|j|||cos =|j|||cos ,化简,得a sin C=c sin A,
所以=.
同理,过点C作与垂直的单位向量m,可得=.
综上可得==.
当△ABC是钝角三角形时,同样可得==.
结论:在一个三角形中,各边和它所对角的正弦的比相等,即==.
思考1:如图,在△ABC中,作AD⊥BC于点D,则c sin B=b sin C=AD,
所以=,
同理可得=,
所以==.
思考2:===2R(R为△ABC外接圆的半径)
例1 在△ABC中 ,由正弦定理=,
得sin B=sin A=×=,
所以B=60°或B=120°.
①当B=60°时,C=180°-45°-60°=75°.
由=,
得c=·a=×16=8(+).
②当B=120°时,C=180°-120°-45°=15°.
由=,
得c=·a=×16=8(-).
综上所述,B=60°,C=75°,c=8(+)或B=120°,C=15°,c=8(-).
跟踪训练1 (1) 在△ABC中,由正弦定理=,
得sin B=sin A=×=.
因为a>b,所以sin A>sin B,即A>B,
所以B=30°,C=180°-45°-30°=105°.
由=,
得c=·a=×16=8(+3).
(2) 因为b sin A=16×=8>8,
所以不存在满足条件的三角形.
跟踪训练2 由正弦定理,得sin C===.
因为c>b,B=30°,
所以30°所以C=45°或C=135°.
①当C=45°时,A=105°.
此时a====+1.
②当C=135°时,A=15°.
此时a====-1.
例2 在△ABC中,B=180°-75°-60°=45°,
由正弦定理,得=,
得c=·b=×100=50,
所以A,B之间的距离c为50 m.
跟踪训练 在△ABD中,设∠ABD=α,
则=,
所以sin α=.
因为AB>AD,所以α<60°,
所以α为锐角,
所以cos α=,A=120°-α,
所以sin A=sin (120°-α)=.
因为=,
所以BD=16.
在△BCD中,由正弦定理,得
=,
所以BC=×sin 30°=8.
思考3:(1)(3)
思考4:已知两边一角(非夹角)或已知两角一边.
【检测反馈】
1. A 解析:由正弦边角关系知a∶b∶c=4∶5∶6,设a=4x,b=5x,c=6x,所以cos C===.
2. C 解析:因为=,所以=.因为在△ABC中,sin A>0,sin B>0,且sin A>sin B,所以=>1,所以a>b.
3. CD 解析:由正弦定理=,得sin B===.又b>a,0°4. 解析:由正弦定理,得=,所以sin B=,又a>b,所以A>B,所以B=,所以C=π-=.
5. (1) 由题意,得(b2+c2-a2)=4S=2bc sin A,
由余弦定理,得2bc cos A=2bc sin A,
所以tan A=,
又A∈(0,π),所以A=.
(2) 由正弦定理,得==,即b=2sin B,c=2sin C,
由(1)知B+C=,
所以b+2c=2sin B+4sin C=2[sin B+2sin (-B)]=4sin B+2cos B=2sin (B+φ),
其中φ∈,sin φ=,cos φ=,故b+2c≤2,
当且仅当B+φ=,即B=-φ时取等号,
故b+2c的最大值为2.
1. 掌握正弦定理,并能解决一些简单的三角形中边与角的计算.
2. 体会“由特殊到一般”的数学思想方法.
活动一 了解正弦定理的探求过程
探究:余弦定理及其推论分别给出了已知两边及其夹角、已知三边直接解三角形的公式.如果已知两角和一边,是否也有相应的直接解三角形的公式呢?
问题1:如图,在Rt△ABC中,C=90°,边a,b,c与角A,B的关系是什么?
问题2:在Rt△ABC中,==,对于锐角三角形和钝角三角形,这个关系式是否仍然成立?如何证明?
结论:正弦定理:
思考1
你能用其他方法推导出正弦定理吗?
思考2
在正弦定理中,比值==与△ABC的外接圆的直径之间存在怎样的关系?
正弦定理指出了三角形中三条边与对应角的正弦之间的关系,描述了三角形中边与角的一种数量关系.
活动二 掌握正弦定理的简单应用
例1 在△ABC中,已知b=16,A=45°,a=16,求角B,C及边c.
(1) 在例1的条件下,将“a=16”改为“a=16”,结论如何?
(2) 在例1的条件下,将“a=16”改为“a=8”,结论又如何?
解三角形有三种情况,两解,一解,无解.要考虑大角对大边,大边对大角,及正弦定理有a>b sin A>sin B,由此确定解的情况.
在△ABC中,已知B=30°,b=,c=2,解这个三角形.
活动三 掌握正弦定理在实际问题中的应用
例2 在△ABC中,已知A=75°,C=60°,A,C之间的距离b为100m,求A,B之间的距离c.
如图,在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.
思考3
下列哪些条件可以直接使用正弦定理来解三角形?
(2)
(3) (4)
思考4
哪些类型的解三角形问题可以直接用正弦定理解决呢?
1. (2023宿迁高一阶段练习)在△ABC中,sin A∶sin B∶sin C=4∶5∶6,则cos C等于( )
A. B. - C. D. -
2. 在△ABC中,角A,B,C所对的边分别为a,b,c,若sin A>sin B,则下列选项中正确的是( )
A. a
3. (多选)在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=,A=30°,则角B的大小为( )
A. 30° B. 150° C. 60° D. 120°
4. 在△ABC中,角A,B,C所对的边分别为a,b,c,若a=3,b=,A=,则角C的大小为________.
5. (2023郑州中牟县第一高级中学高一阶段练习)已知△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,且(b2+c2-a2)=4S.
(1) 求角A的大小;
(2) 若a=,求b+2c的最大值.
【答案解析】
6.4.4 正弦定理(1)
【活动方案】
问题1:sin A=,sin B=.
问题2:成立,证明如下:
在锐角三角形ABC中,过点A作与垂直的单位向量j,则j与的夹角为-A,j与的夹角为-C.
因为+=,
所以j·(+)=j·,
即|j|||cos +|j|||cos =|j|||cos ,化简,得a sin C=c sin A,
所以=.
同理,过点C作与垂直的单位向量m,可得=.
综上可得==.
当△ABC是钝角三角形时,同样可得==.
结论:在一个三角形中,各边和它所对角的正弦的比相等,即==.
思考1:如图,在△ABC中,作AD⊥BC于点D,则c sin B=b sin C=AD,
所以=,
同理可得=,
所以==.
思考2:===2R(R为△ABC外接圆的半径)
例1 在△ABC中 ,由正弦定理=,
得sin B=sin A=×=,
所以B=60°或B=120°.
①当B=60°时,C=180°-45°-60°=75°.
由=,
得c=·a=×16=8(+).
②当B=120°时,C=180°-120°-45°=15°.
由=,
得c=·a=×16=8(-).
综上所述,B=60°,C=75°,c=8(+)或B=120°,C=15°,c=8(-).
跟踪训练1 (1) 在△ABC中,由正弦定理=,
得sin B=sin A=×=.
因为a>b,所以sin A>sin B,即A>B,
所以B=30°,C=180°-45°-30°=105°.
由=,
得c=·a=×16=8(+3).
(2) 因为b sin A=16×=8>8,
所以不存在满足条件的三角形.
跟踪训练2 由正弦定理,得sin C===.
因为c>b,B=30°,
所以30°
①当C=45°时,A=105°.
此时a====+1.
②当C=135°时,A=15°.
此时a====-1.
例2 在△ABC中,B=180°-75°-60°=45°,
由正弦定理,得=,
得c=·b=×100=50,
所以A,B之间的距离c为50 m.
跟踪训练 在△ABD中,设∠ABD=α,
则=,
所以sin α=.
因为AB>AD,所以α<60°,
所以α为锐角,
所以cos α=,A=120°-α,
所以sin A=sin (120°-α)=.
因为=,
所以BD=16.
在△BCD中,由正弦定理,得
=,
所以BC=×sin 30°=8.
思考3:(1)(3)
思考4:已知两边一角(非夹角)或已知两角一边.
【检测反馈】
1. A 解析:由正弦边角关系知a∶b∶c=4∶5∶6,设a=4x,b=5x,c=6x,所以cos C===.
2. C 解析:因为=,所以=.因为在△ABC中,sin A>0,sin B>0,且sin A>sin B,所以=>1,所以a>b.
3. CD 解析:由正弦定理=,得sin B===.又b>a,0°
5. (1) 由题意,得(b2+c2-a2)=4S=2bc sin A,
由余弦定理,得2bc cos A=2bc sin A,
所以tan A=,
又A∈(0,π),所以A=.
(2) 由正弦定理,得==,即b=2sin B,c=2sin C,
由(1)知B+C=,
所以b+2c=2sin B+4sin C=2[sin B+2sin (-B)]=4sin B+2cos B=2sin (B+φ),
其中φ∈,sin φ=,cos φ=,故b+2c≤2,
当且仅当B+φ=,即B=-φ时取等号,
故b+2c的最大值为2.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
