第2章整式的加减复习教材全解(重难点、例题解析)
文档属性
| 名称 | 第2章整式的加减复习教材全解(重难点、例题解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 619.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-13 00:00:00 | ||
图片预览




文档简介
登陆21世纪教育 助您教考全无忧
新人教版七年级数学上册
第2章整式的加减复习教材全解(重难点、例题解析)
复习内容:
列式表示数量关系、单项式、多项式、整式等有关概念以及整式加减运算.
复习目标:
1.知识与技能
进一步理解单项式、多项式、整式及其有关概念,准确确定单项式的系数、次数、多项式的项、次数;理解同类项概念,掌握合并同类项法则和去括号规律,熟练地进行整式加减运算.
2.过程与方法
通过回顾与思考,帮助学生梳理本章内容,提高学生分析、归纳、语言表达能力;提高运算能力及综合应用数学知识的能力.
3.情感态度与价值观
培养严谨的学习态度和积极思考的学习习惯,通过列式表示数量关系,体会数学知识与实际问题的联系.
一、本章知识结构框架图
二、易错知题分析
误区一 书写不规范致误
例1 用代数式表示下列语句:
(1)比x与y的和的平方小x与y的和的数
(2)a的2倍与b的的差除以a与b的差的立方。
错解(1)()-(x+y) (2)(2a-1/3b)÷(x+y)
剖析:(1)要表示的是“比x与y的和的平方小x与y的和的数”,应该先求和再求平方即应该是,而不应该是()-(x+y)。(2)是书写不规范,除号要用分数线代替,即应该写成。
正解:(1) (2)
误区二 概念不清致误
例2、判断下列各组是否是同类项:
(1)0.2x2y与0.2xy2 (2)4abc与4ac (3)-130与15 (4)与
(5) (6)
错解:(1)(3)(4)(6)是同类项,(2)(5)不是同类项。
剖析:(1)0.2x2y与0.2xy2因为字母x的指数不同,字母y的指数也不同,所以不是同类项。
(2)4abc与4ac,显然第二个单项式中没有字母b所以不是同类项。
(3)都是单独一个数-130和15,是同类项。
(4)虽然与字母的排列顺序不同,但相同字母m的指数相同,n的指数相同,字母也相同,所以是同类项。
(5)将(a+b)看成一个整体,那么是同类项。
(6)中,字母相同都是p,q并且字母p的指数都是n+1,q的指数都是n,也相同,所以是同类项。
解:(1)、(2)不是同类项 (3)、(4)、(5)、(6)是同类项。
说明:根据同类项的定义判断,同类项应所含字母相同,并且相同字母的指数也分别相同,同类项与系数无关,与字母的顺序无关。
(1)题相同字母的指数不相同; (2)题所含字母不同; (5)题将(a+b)看作一个整体。
误区三 去括号致错
例3 计算
错解:原式==
剖析:去括号时,括号前是“-”号,把括号和它前面的“-”号去掉,括号内各项都要变号,本题是最常见的错误:只改变括号内第一项的符号而忘记改变其余各项的符号。
正解:原式
(2)括号前的系数不是1
例4 计算
错解1:原式 错解2:原式
剖析: 去括号时,若括号前的系数不是1,则要按分配律来计算,即要用括号外的系数乘以括号内的每一项。本题就是常见的错误:“变符号”与使用“分配律”顾此失彼。
正解:原式==
三、经典题型分析
题型一 列代数式
1.列代数式的关键是正确掌握数学关联词。
2.书写代数式时应注意规范:
①代数式中用到乘号,若是数字与数字相乘,要用“×”号;若是数字与字母或字母与字母相乘,通常简写成“·”号或省略不写。
②数字与字母相乘时,要把数字写在字母的前面,如“a的2倍”写成“2a”而不“a2”。若是带分数与字母相乘,应把带分数化为假分数,如“而不是”
③代数式中的除的关系,一般应写成分数形式。如a÷2=。
④多项式后面跟单位的,要给多项式加括号,如(ab+cd)平方米。
例1]用代数式表示
(1)a的2倍与b的一半之和的平方,减去a、b两数平方和的2倍。
(2)与x的积与3除y的商的和。
(3)甲、乙两数之和是25,甲为a,求比乙的2倍小7的数的立方。
(4)甲为x,乙为y,求甲、乙两数积与乙数倒数的差。
分析:注意和、差、倍、和的平方、平方和这些关联词表达的意思。
解:(1) (2) HYPERLINK "http://www.1230.org" EMBED Equation.2 (3) (4)
点拨: 和是加法运算的结果,差是减法运算的结果,积是乘法运算的结果,商是除法运算的结果,和的平方是先求和再求平方,平方和是先求平方再求和,顺序不同。
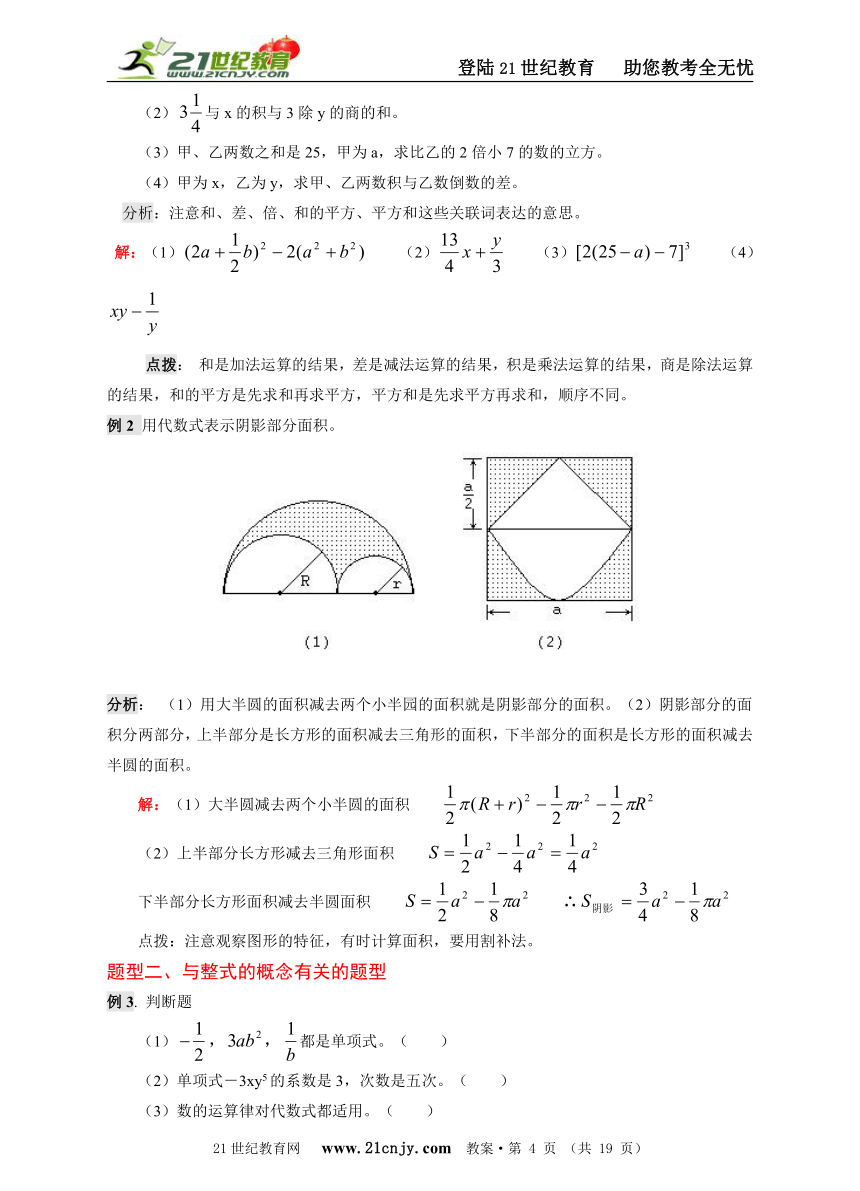
例2 用代数式表示阴影部分面积。
分析: (1)用大半圆的面积减去两个小半园的面积就是阴影部分的面积。(2)阴影部分的面积分两部分,上半部分是长方形的面积减去三角形的面积,下半部分的面积是长方形的面积减去半圆的面积。
解:(1)大半圆减去两个小半圆的面积
(2)上半部分长方形减去三角形面积
下半部分长方形面积减去半圆面积 ∴
点拨:注意观察图形的特征,有时计算面积,要用割补法。
题型二、与整式的概念有关的题型
例3. 判断题
(1)都是单项式。( )
(2)单项式-3xy5的系数是3,次数是五次。( )
(3)数的运算律对代数式都适用。( )
分析:
(1)只有数与字母的积的运算的代数式叫做单项式,其中包括单独一个数或一个字母。而的分母中含有字母,是数与字母的商,所以它不是单项式。
(2)单项式中的数字因数叫做这个单项式的系数,-3xy5中数字因数是-3,而不是3。就是说系数包括前面的符号。
单项式的次数是单项式中所有字母的指数的和。所以-3xy5的次数是1+5即六次而不是五次。-3xy5就是-3xyyyyy它有六个字母因数,是六次。
(3)数的运算律对代数式都适用。
解:(1)×(2)×(3)√
点拨:做判断题时,概念一定要清楚,要仔细阅读题目。
例4. 已知多项式,,
(1)求多项式中各项的系数和次数。 (2)若多项式是八次三项式,求m的值。
分析:(1)多项式中第一项的系数是4。次数应为所有字母指数的和,所以是2m+1+1=2m+2。第二项-5x2y2的系数是-5,次数为2+2=4。第三项-31x5y的系数是-31,次数是5+1=6。
(2)因为多项式中第二项是4次的,第三项是6次的,均已确定,所以只能第一项是八次的。由(1)知2m+2=8,∴m=3。
解:(1)y的系数是4,次数是2m+2。 -5x2y2的系数是-5,次数是4。
-31x5y的系数是-31,次数是6。
(2)由(1)中2m+2=8,解得m=3。
点拨:对于第一个单项式的次数是2m+2可能感到并不习惯,通过多次练习,这样对于字母表示数、次数会有较深的认识。在(2)问中由于多项式是八次三项式,而第二项、第三项的次数分别是4次、6次,故只有第一项应是8次,可得方程,求出m的值。
例5. 给出多项式6a2b2-3ab+4a4b-8b5+7a3,分别回答下列问题:
(1)是几项式? (2)是几次式? (3)字母a的最高次数是多少? (4)字母b的最高次数是多少? (5)把多项式按a的降幂重新排列; (6)把多项式按b的降幂重新排列。
分析:只要把多项式的项数和次数概念弄清楚,(1)(2)是不难回答的。对于(3)和(4)回答时注意只看题目所要求的字母的次数,而不管其它字母。例如(3)因为多项式6a2b2-3ab+4a4b-8b5+7a3中含有字母a的各项中。a的指数最大的是4,所以字母a的最高次数是4。
同样道理可知字母b的最高次数是5。
解:(1)五项式; (2)五次式; (3)a的最高次数是4; (4)b的最高次数是5;
(5)4a4b+7a3+6a2b2-3ab3-8b5; (6)-8b5-3ab3+6a2b2+4a4b+7a3。
点拨:按某一个字母把多项式写成降幂排列(或升幂排列)实际是把这个字母看成主要字母、找出它的次数的大小,利用加法交换律按顺序写出来。此时与其它字母无关。
例6、已知是同类项,求5m+3n的值。
分析:所含字母相同,相同字母的指数也相同的项是同类项,所以,由x的指数相同可得:3m-1=5,m=2;由y的指数相同可得:2n+1=3,n=1,再代入5m+3n中求值即可。
解:因为是同类项,所以3m-1=5,m=2;同时2n+1=3,n=1;所以5m+3n=5×2+3×1=13。
点拨:同类项是所含字母相同,相同字母的指数也相同的项,根据同类项的定义可得字母指数的方程,然后再求代数式的值。
题型三、求代数式的值
例7、 a是绝对值等于2的负数,b是最小的正整数,c的倒数的相反数是。求代数式的值。
分析:由已知条件可知,然后化简代数式,最后将已知条件代入求值。
解:∵a是绝对值等于2的负数,∴
∵b是最小的正整数,∴
再∵c的倒数的相反数是
HYPERLINK "http://www.1230.org" EMBED Equation.2
点拨:求代数式值的题目,一般是找到代数式中的字母的值,将代数式化简后代入求值。
例8. 当时,求的值。
分析:本题中根据已知条件很难求出a,b的值,观察到互为倒数,可把分别看作一个“整体”,将“整体”的值直接代入求值式,这样就可以避免求其中字母的值,简化了求值过程。这种求代数式值的方法叫整体代入法。
解:∵
∴。
点拨:求代数式的值,一般用化简求值法,但当代数式中字母的值很难求,而所给的题目又有一定的特殊性时,我们观察到含未知数的部分可以看成一个整体时,我们用整体代入法,这样会使运算简便,问题得解。
例9
分析:根据所给已知条件先求出代数式中字母的值,再代入求值。求字母的值时要根据绝对值是非负数,完全平方也是非负数,两个非负数的和为0,这两个非负数都是0来列方程,求字母的值。
解:
点拨:绝对值和完全平方数是非负数,这个知识点常考到,要注意体会本题是如何用这个非负性的。
例10
分析:所给的条件很难求出两个字母的值,所以考虑用整体代入法求值。
解:
HYPERLINK "http://www.1230.org" EMBED Equation.2
点拨:当发现题目可用整体代入法求值时,关键就在把代数式变形,成为可整体代入的形式。这是变形的方向。
题型四:与整式的加减有关的题型
例11 从某整式减去,因误认为加上此式,则答案为,试求正确答案。
分析:若设某整式为A,令。本题要求是,而误作为了,这可由得到正确答案。此技巧也是整体思想的又一体现。
解:
故正确答案是。
点拨:要清楚本题要求是,而误作为了,这可由来求解。这个变形要能理解,这是解本题的关键。
例12、设,请说明的值与x的取值无关。
分析:所给多项式的值与x无关,即要求多项式 ( http: / / www.1230.org )的值不含x,所以要将A、B、C所表示的代数式代入进行加减运算,最后所得的结果中不含x,就能说明的值与x的取值无关。
解:
∵4为常数项 ∴结论成立
点拨:把A、B、C表示的多项式看成一个整体,用括号括起来,以减少符号方面的错误。
题型五、比较代数式大小
例13、 设,当时,试比较A与B的值的大小。
分析: 方法一:先分别求出代数式A与B当时的值,再比较这两个值的大小;这种比较大小的方法叫求值比大小。
方法二:我们知道,
如果,那么; 如果,那么; 如果,那么。
根据上述规律,我们可以先计算(注意合并同类项),再当,时,求代数式的值,于是,根据这个值的符号(正、零或负),就能断定A与B的大小。这种比较大小的方法叫求差比较法
解法一:
解法二:
当时,
原式
点拨:求差比较法不仅体现了一个重要的数学思想,而且使用起来常常比求值比较法更为简便。
例14. 比较与a的大小。
分析:在代数式和a中,都有同一字母a,所以,不论a为何值,都不会影响与a的大小关系,因此,只要分情况讨论b就可以了。
解一:当时,;
当时,;
当时,。
解二、-a=b,所以,当时,-a>0,即;
当时,;
当时,。
点拨:本题分析比大小和做差比较大小时都发现要进行分类讨论,注意分类要既不重复也不遗漏。
四、中考题型分析
题型一:去括号、合并同类项的题
例1、(2006年长春市) 化简的结果是 ( )
(A)0. (B)2. (C). (D).
分析:本题是去括号、合并同类项的基础题,只要按去括号法则运算即可。
解:。=,所以选C
题型二:求值题
例2、(苏州市2006年) 若x=2,则的值是 ( )
(A) (B)1 (C)4 (D)8
分析:本题也是求值题中的基本题,直接代入求值即可。
解:;所以选B。
例3、(张家界市2006年)13.已知,那么:___________.
分析:本题根据已知条件很难求得x和y的值,所以考虑用整体代入法求值。
解:因为,所以
点拨:求代数式值的题型,一般的解题思路是先化简再代入计算求值。但代数式中字母值很难求时考虑用整体代入法。一般整体代入法求值的题目有一定的特征,就是含未知数的部分可以看成一个整体。
题型三:列代数式题
例4(湖北省荆门市二00六年)6.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
(A)a2-b2=(a+b)(a-b). (B)(a+b)2=a2+2ab+b2.
(C)(a-b)2=a2-2ab+b2. (D)a2-b2=(a-b)2.
分析:图(1)阴影部分的面积是a2-b2,图(2)阴影部分的面积是:,由于阴影部分面积相等,所以选A。
解:选A。
题型五 找规律题型
例5、(常德市,2005)找规律:如图,第(1)幅图中有1个菱形,第(2)幅图中有3个菱形,第(3)幅图中有5个菱形,则第(n)幅图中共有___________个菱形。
分析:第(1)幅图中有1个菱形,第(2)幅图中有3个菱形,第(3)幅图中有5个菱形,第(4)幅图中有7个菱形,所以第(n)幅图中有(2n-1)个菱形。
解:有(2n-1)个
第二章单元测试题
一、选择题(本大题共12题,每小题2分,共24分,每小题只有一个正确选项,把正确选项的代号填在题后的括号里)
1.、在下列代数式:中,单项式有( )
(A)3个 (B)4个 (C)5个 (D)6个
2、.在下列代数式:中,多项式有( )(A)2个 (B)3个 (C)4个 (D)5个
为( )
A. 2 B. 3 C. 4 D. 5
4、. 下列说法中正确的是( )
A. 5不是单项式
5.
A. x与y的一半的差 B. x与y的差的一半 C. x减去y除以2的差
7. 下列各组中,当n=3时是同类项的是( )
8、下列整式加减正确的是【 】
(A)2x-(x2+2x)=-x2 (B)2x-(x2-2x)=x2
(C)2x+(y+2x)=y (D)2x-(x2-2x)=x2
9、减去-2x后,等于4x2-3x-5的代数式是【 】
(A)4x2-5x-5 (B)-4x2+5x+5 (C)4x2-x-5 (D)4x2-5
10.、一个多项式加上3x2y-3xy2得x3-3x2y,这个多项式是【 】
(A)x3+3xy2 (B)x3-3xy2 (C)x3-6x2y+3xy2 (D)x3-6x2y-3xy2
11、. 把,正确的是( )
A. B. C. HYPERLINK "http://www.1230.org" EMBED Equation.2 D.
12、(安徽省,2005)今天,和你一起参加全省课改实验区初中毕业学业考试的同学约有15万人,其中男生约有a万人,则女生约有( )
A、(15+a)万人 B、(15-a)万人 C、15a万人 D、万人
二、填空题(本题共8小题,每小题3分,共24分)
13. 一个三位数,它的个位数字是0,十位数字是a,百位数字是b,用代数式表示这个三位数是__________。
14.若单项式-2x3yn-3是一个关于x,y的5次单项式,则n=_________.
15.若多项式(m+2)y2-3xy3是五次二项式,则m=___________.
16.化简2x-(5a-7x-2a)=__________。
17、. 当时,代数式的值是____________。
18、 已知,则代数式____________。
19、 已知,则代数式____________。
20、 已知长方形的长为a,面积是16,它的宽为________。
三、解答题:(21、22、23、25、26、27每题8分,24题6分)
21、. 补入下列各多项式的缺项,并按x的升幂排列:
(1)-x3+x-2 (2)x4-5-x2 (3)x3-1 (4)1-x4
22、比较下列各式的大小:
(1)比较和的大小。(2) 比较与的大小
23、.
24、已知长方形ABCD中,AB=4cm,AD=2cm,以AB为直径作一个半圆,求阴影部分面积。
26、
27、. 某移动通讯公司开设了两种通讯业务:①“全球通”用户先交50元月租费,然后每通话一分钟,付话费0.6元(市内通话);②“快捷通”,用户不交月租费,每通话一分钟,付话费0.8元(市内通话)。
(1)按一个月通话x分钟计,请你写出两种收费方式下客户应支付的费用;
(2)某用户一个月内市内通话时间为200分钟,选择哪种通讯业务较省钱?
答案:
1、 选择题:
1、 B;分析:数与字母的积叫单项式,单独一个字母或数也是单项式。所以 是单项式,故选B。点拨:注意单项式的定义,代数式中只有数与字母的积,单独一个数字和字母也是单项式。
2、B;分析:几个单项式的和是多项式,要注意分别是一个常数,所以这两个都是单项式;多项式是:,故选B。点拨:由于单独一个数和字母也是单项式,所以是单项式而不是多项式。
3. B ;分析:多项式为八次四项式,就是说有四项,最高次项是八,所以2m+1=7,m=3,所以选B。点拨:多项式的次数是多项式中次数最高项的次数,所以要把每一项的次数都算出来,本题字母是a和b,m是常数,所以只有这一项的次数可能是八次。
4、C。 分析:单项式和多项式统称整式,数与字母的积叫单项式,数字因数叫单项式的系数,所以5是单项式,,,只有。故选C。点拨:单项式和多项式统称整式,而单项式和多项式中只有加、减、乘的运算,当分母中含有字母时一定有除法运算,所以分母中含有字母的代数式决不是整式。
5. B;分析: HYPERLINK "http://www.1230.org" EMBED Equation.2 点拨:根据一些语句列代数式,或根据代数式说出代数式的意义,都要求我们要注意描述运算的关联词。
6. A ;分析:去括号合并同类项就可得结果。点拨:注意第二个括号前是-2,表示-2与括号中的每一项相乘,再把所得的积相加。
7. D ;分析:把n=3代入每一个答案中看相同字母的指数是否相同,如果相同字母的指数也相同就是同类项。点拨:本题也可以一个答案一个答案的看,如果是同类项那么n应该取什么值,看哪个n取3就选哪个,不过这个方法不如第一个方法简单。
8、A;分析:把每个答案去括号合并同类项,看是否等于右边。点拨:注意去括号法则,括号前面是负号,把负号和括号去掉,括号中的每一项都要改变符号。
9、A;分析:设所求代数式为A,则有:A-(-2x)=4x2-3x-5,所以A=4x2-3x-5+(-2x)=4x2-3x-5-2x=4x2-5x-5,所以选A。点拨:已知差和减数,求被减数用加法,被减数=差+减数。所以所求代数式是差的代数式加上减去的代数式。
10、C;分析:设所求代数式为A,则有A+3x2y-3xy2=x3-3x2y,所以A=x3-3x2y-(3x2y-3xy2)=x3-3x2y-3x2y+3xy2=x3-6x2y+3xy2,所以选C。点拨:已知和和其中一个加数,求另一个加数用减法,另一个加数=和-其中一个加数。
11、D。 分析:注意字母换成数,运算顺序和符号不变,所以选D。点拨:代入求值要把代数式的含义搞清楚,要理解代数式中的运算。
12、 B;分析:参加全省课改实验区初中毕业学业考试的学生人数=男生人数+女生人数,所以女生人数=总人数-男生人数。点拨:多项式后面跟单位,要给多项式加括号。
二、填空题
13. ;分析:三位数=百位数字×100+十位数字×10+个位数字;点拨:三位数的表示方法不是abc,这样写的abc式相乘的关系,不表示三位数,所以三位数=百位数字×100+十位数字×10+个位数字。
14、n=5;分析:单项式的次数是所有字母的指数和,因为单项式-2x3yn-3是一个关于x,y的5次单项式,所以3+n-3=5,n=5。点拨:单项式的次数是所有字母的指数和,当已知单项式次数时,可根据单项式的次数列方程,从而求出字母指数的值。
15、;分析:多项式(m+2)y2-3xy3是五次二项式,所以;点拨:多项式的次数是多项式中次数最高项的次数,所以可得方程:到这里考虑平方为4的数有几个?因为,所以。
16、11x-3a;解析:2x-(5a-7x-2a)=2x-5a+7x+2a=11x-3a;点拨:去括号合并同类项时要注意括号前是负号,把括号和负号去掉,括号中的每一项都要变号。
17、;分析:因为,所以=;点拨:把字母的值代入代数式中,代数式所表示的运算不变,即注意字母换成数,运算顺序和符号不变。
18、 ,解析:因为,它的倒数,所以;点拨:所给的已知条件很难求出a与b的值,观察代数式中出现a、b的地方都有一定的特点,所以考虑用整体代入法求值。
19、73;解析: (8x+8y)+5xy=8(x+y)+5xy=8×+5×()=124-51=73。点拨:所给的已知条件无法求出x与y的值,所以考虑将代数式变形整体代入求值。
20、;分析:长方形的面积=长×宽,所以,宽=面积÷长。点拨:除法要写成分数的形式。
三:解答题
21、 解:(1)-2+x+0x2-x3
(2)-5+0x-x2+0x3+x4
(3)-1+0x+0x2+x3
(4)1+0x+0x2+0x3-x4
点拨:补缺项,要先确定现在有哪些项,再观察缺哪些项。因为不能改变多项式的值,所以只能让补入的项系数为0,例如(1)x3+x-2是三次多项式,按x的升幂排列,把(1)-x3+x-2中的各项填入相应的位置,观察发现缺二次项,于是把0x2填入二次项的位置。
常数项 一次项 二次项 三次项
-2 +x 0x2 -x3
同样道理(2)x4-5-x2是4次多项式,应有5项,把x4-5-x2中各项填入相应的位置,观察发现缺一次项和三次项,于是把0x和0x3填入相应的位置。
常数项 一次项 二次项 三次项 四次项
-5 0x -x2 0x3 x4
同样方法可知(3)缺一次项和二次项,(4)缺一次项,二次项,三次项。
有时按升幂排列,也有时需要按降幂排列,方法是类似的。重新排列时注意各项要连同它前面的符号一起移动。
22、 解:(1)
(2) 解一(分析比较法):当时,;
当时,;
当时,。
解二(求差比较法):
∴当时,;
当时,;
当时,
点拨:比较代数式的大小,常用的方法是求差比较法,有时也用分析法。如果求差以后的结果含有字母,那么需要分类讨论。如(2)的解法一:在和中,完全相同的部分是a,b与-b是不同的,所以只要讨论b与-b的大小关系就可以了。解法二求差得2b,所以要对b进行讨论。
23、解:
点拨:整式的加减运算,要把每个整式看成一个整体,加括号以后再进行运算。
24. 解:阴影部分的面积=长方形面积-半圆的面积,所以,阴影部分的面积=4×2-=,所以阴影部分的面积为。
点拨:观察图形可知阴影部分的面积=长方形面积-半圆的面积,这是列代数式的根据。
25、.若代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a、b的值。
解:(x2+ax-2y+7)-(bx2-2x+9y-1)=x2+ax-2y+7-bx2+2x-9y+1=,因为代数式的值与x无关,所以1-b=0,b=1;a+2=0,a=-2。
点拨:代数式的值与x无关,即合并同类项后不含x ( http: / / www.1230.org )项,也就是含x项的系数为0。
26、. 解:
点拨:由于已知条件中很难求出a和b的值,所以考虑能否用整体代入法。整理化简代数式,发现可以表示成(a-b)和ab的形式,所以可以把
27、解: (1)“全球通”客户支付的费用为:(50+0.6x)元
“快捷通”客户支付的费用为:0.8x元
(2)把x=200分别代入上面两个代数式,得
因为170>160
所以选择“快捷通”业务较省钱。
点拨:“全球通”客户支付的费用=先交的月租50元+0.6×通话分钟数;“快捷通”,用户支付的费用=0.8×通话分钟数。
丰富的问题情景
代数式
单项式
多项式
整式
同类项
合并同类项
去括号、添括号法则
整式加减法
系数
次数
项
列代数式
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 教案·第 18 页 (共 18 页)
新人教版七年级数学上册
第2章整式的加减复习教材全解(重难点、例题解析)
复习内容:
列式表示数量关系、单项式、多项式、整式等有关概念以及整式加减运算.
复习目标:
1.知识与技能
进一步理解单项式、多项式、整式及其有关概念,准确确定单项式的系数、次数、多项式的项、次数;理解同类项概念,掌握合并同类项法则和去括号规律,熟练地进行整式加减运算.
2.过程与方法
通过回顾与思考,帮助学生梳理本章内容,提高学生分析、归纳、语言表达能力;提高运算能力及综合应用数学知识的能力.
3.情感态度与价值观
培养严谨的学习态度和积极思考的学习习惯,通过列式表示数量关系,体会数学知识与实际问题的联系.
一、本章知识结构框架图
二、易错知题分析
误区一 书写不规范致误
例1 用代数式表示下列语句:
(1)比x与y的和的平方小x与y的和的数
(2)a的2倍与b的的差除以a与b的差的立方。
错解(1)()-(x+y) (2)(2a-1/3b)÷(x+y)
剖析:(1)要表示的是“比x与y的和的平方小x与y的和的数”,应该先求和再求平方即应该是,而不应该是()-(x+y)。(2)是书写不规范,除号要用分数线代替,即应该写成。
正解:(1) (2)
误区二 概念不清致误
例2、判断下列各组是否是同类项:
(1)0.2x2y与0.2xy2 (2)4abc与4ac (3)-130与15 (4)与
(5) (6)
错解:(1)(3)(4)(6)是同类项,(2)(5)不是同类项。
剖析:(1)0.2x2y与0.2xy2因为字母x的指数不同,字母y的指数也不同,所以不是同类项。
(2)4abc与4ac,显然第二个单项式中没有字母b所以不是同类项。
(3)都是单独一个数-130和15,是同类项。
(4)虽然与字母的排列顺序不同,但相同字母m的指数相同,n的指数相同,字母也相同,所以是同类项。
(5)将(a+b)看成一个整体,那么是同类项。
(6)中,字母相同都是p,q并且字母p的指数都是n+1,q的指数都是n,也相同,所以是同类项。
解:(1)、(2)不是同类项 (3)、(4)、(5)、(6)是同类项。
说明:根据同类项的定义判断,同类项应所含字母相同,并且相同字母的指数也分别相同,同类项与系数无关,与字母的顺序无关。
(1)题相同字母的指数不相同; (2)题所含字母不同; (5)题将(a+b)看作一个整体。
误区三 去括号致错
例3 计算
错解:原式==
剖析:去括号时,括号前是“-”号,把括号和它前面的“-”号去掉,括号内各项都要变号,本题是最常见的错误:只改变括号内第一项的符号而忘记改变其余各项的符号。
正解:原式
(2)括号前的系数不是1
例4 计算
错解1:原式 错解2:原式
剖析: 去括号时,若括号前的系数不是1,则要按分配律来计算,即要用括号外的系数乘以括号内的每一项。本题就是常见的错误:“变符号”与使用“分配律”顾此失彼。
正解:原式==
三、经典题型分析
题型一 列代数式
1.列代数式的关键是正确掌握数学关联词。
2.书写代数式时应注意规范:
①代数式中用到乘号,若是数字与数字相乘,要用“×”号;若是数字与字母或字母与字母相乘,通常简写成“·”号或省略不写。
②数字与字母相乘时,要把数字写在字母的前面,如“a的2倍”写成“2a”而不“a2”。若是带分数与字母相乘,应把带分数化为假分数,如“而不是”
③代数式中的除的关系,一般应写成分数形式。如a÷2=。
④多项式后面跟单位的,要给多项式加括号,如(ab+cd)平方米。
例1]用代数式表示
(1)a的2倍与b的一半之和的平方,减去a、b两数平方和的2倍。
(2)与x的积与3除y的商的和。
(3)甲、乙两数之和是25,甲为a,求比乙的2倍小7的数的立方。
(4)甲为x,乙为y,求甲、乙两数积与乙数倒数的差。
分析:注意和、差、倍、和的平方、平方和这些关联词表达的意思。
解:(1) (2) HYPERLINK "http://www.1230.org" EMBED Equation.2 (3) (4)
点拨: 和是加法运算的结果,差是减法运算的结果,积是乘法运算的结果,商是除法运算的结果,和的平方是先求和再求平方,平方和是先求平方再求和,顺序不同。
例2 用代数式表示阴影部分面积。
分析: (1)用大半圆的面积减去两个小半园的面积就是阴影部分的面积。(2)阴影部分的面积分两部分,上半部分是长方形的面积减去三角形的面积,下半部分的面积是长方形的面积减去半圆的面积。
解:(1)大半圆减去两个小半圆的面积
(2)上半部分长方形减去三角形面积
下半部分长方形面积减去半圆面积 ∴
点拨:注意观察图形的特征,有时计算面积,要用割补法。
题型二、与整式的概念有关的题型
例3. 判断题
(1)都是单项式。( )
(2)单项式-3xy5的系数是3,次数是五次。( )
(3)数的运算律对代数式都适用。( )
分析:
(1)只有数与字母的积的运算的代数式叫做单项式,其中包括单独一个数或一个字母。而的分母中含有字母,是数与字母的商,所以它不是单项式。
(2)单项式中的数字因数叫做这个单项式的系数,-3xy5中数字因数是-3,而不是3。就是说系数包括前面的符号。
单项式的次数是单项式中所有字母的指数的和。所以-3xy5的次数是1+5即六次而不是五次。-3xy5就是-3xyyyyy它有六个字母因数,是六次。
(3)数的运算律对代数式都适用。
解:(1)×(2)×(3)√
点拨:做判断题时,概念一定要清楚,要仔细阅读题目。
例4. 已知多项式,,
(1)求多项式中各项的系数和次数。 (2)若多项式是八次三项式,求m的值。
分析:(1)多项式中第一项的系数是4。次数应为所有字母指数的和,所以是2m+1+1=2m+2。第二项-5x2y2的系数是-5,次数为2+2=4。第三项-31x5y的系数是-31,次数是5+1=6。
(2)因为多项式中第二项是4次的,第三项是6次的,均已确定,所以只能第一项是八次的。由(1)知2m+2=8,∴m=3。
解:(1)y的系数是4,次数是2m+2。 -5x2y2的系数是-5,次数是4。
-31x5y的系数是-31,次数是6。
(2)由(1)中2m+2=8,解得m=3。
点拨:对于第一个单项式的次数是2m+2可能感到并不习惯,通过多次练习,这样对于字母表示数、次数会有较深的认识。在(2)问中由于多项式是八次三项式,而第二项、第三项的次数分别是4次、6次,故只有第一项应是8次,可得方程,求出m的值。
例5. 给出多项式6a2b2-3ab+4a4b-8b5+7a3,分别回答下列问题:
(1)是几项式? (2)是几次式? (3)字母a的最高次数是多少? (4)字母b的最高次数是多少? (5)把多项式按a的降幂重新排列; (6)把多项式按b的降幂重新排列。
分析:只要把多项式的项数和次数概念弄清楚,(1)(2)是不难回答的。对于(3)和(4)回答时注意只看题目所要求的字母的次数,而不管其它字母。例如(3)因为多项式6a2b2-3ab+4a4b-8b5+7a3中含有字母a的各项中。a的指数最大的是4,所以字母a的最高次数是4。
同样道理可知字母b的最高次数是5。
解:(1)五项式; (2)五次式; (3)a的最高次数是4; (4)b的最高次数是5;
(5)4a4b+7a3+6a2b2-3ab3-8b5; (6)-8b5-3ab3+6a2b2+4a4b+7a3。
点拨:按某一个字母把多项式写成降幂排列(或升幂排列)实际是把这个字母看成主要字母、找出它的次数的大小,利用加法交换律按顺序写出来。此时与其它字母无关。
例6、已知是同类项,求5m+3n的值。
分析:所含字母相同,相同字母的指数也相同的项是同类项,所以,由x的指数相同可得:3m-1=5,m=2;由y的指数相同可得:2n+1=3,n=1,再代入5m+3n中求值即可。
解:因为是同类项,所以3m-1=5,m=2;同时2n+1=3,n=1;所以5m+3n=5×2+3×1=13。
点拨:同类项是所含字母相同,相同字母的指数也相同的项,根据同类项的定义可得字母指数的方程,然后再求代数式的值。
题型三、求代数式的值
例7、 a是绝对值等于2的负数,b是最小的正整数,c的倒数的相反数是。求代数式的值。
分析:由已知条件可知,然后化简代数式,最后将已知条件代入求值。
解:∵a是绝对值等于2的负数,∴
∵b是最小的正整数,∴
再∵c的倒数的相反数是
HYPERLINK "http://www.1230.org" EMBED Equation.2
点拨:求代数式值的题目,一般是找到代数式中的字母的值,将代数式化简后代入求值。
例8. 当时,求的值。
分析:本题中根据已知条件很难求出a,b的值,观察到互为倒数,可把分别看作一个“整体”,将“整体”的值直接代入求值式,这样就可以避免求其中字母的值,简化了求值过程。这种求代数式值的方法叫整体代入法。
解:∵
∴。
点拨:求代数式的值,一般用化简求值法,但当代数式中字母的值很难求,而所给的题目又有一定的特殊性时,我们观察到含未知数的部分可以看成一个整体时,我们用整体代入法,这样会使运算简便,问题得解。
例9
分析:根据所给已知条件先求出代数式中字母的值,再代入求值。求字母的值时要根据绝对值是非负数,完全平方也是非负数,两个非负数的和为0,这两个非负数都是0来列方程,求字母的值。
解:
点拨:绝对值和完全平方数是非负数,这个知识点常考到,要注意体会本题是如何用这个非负性的。
例10
分析:所给的条件很难求出两个字母的值,所以考虑用整体代入法求值。
解:
HYPERLINK "http://www.1230.org" EMBED Equation.2
点拨:当发现题目可用整体代入法求值时,关键就在把代数式变形,成为可整体代入的形式。这是变形的方向。
题型四:与整式的加减有关的题型
例11 从某整式减去,因误认为加上此式,则答案为,试求正确答案。
分析:若设某整式为A,令。本题要求是,而误作为了,这可由得到正确答案。此技巧也是整体思想的又一体现。
解:
故正确答案是。
点拨:要清楚本题要求是,而误作为了,这可由来求解。这个变形要能理解,这是解本题的关键。
例12、设,请说明的值与x的取值无关。
分析:所给多项式的值与x无关,即要求多项式 ( http: / / www.1230.org )的值不含x,所以要将A、B、C所表示的代数式代入进行加减运算,最后所得的结果中不含x,就能说明的值与x的取值无关。
解:
∵4为常数项 ∴结论成立
点拨:把A、B、C表示的多项式看成一个整体,用括号括起来,以减少符号方面的错误。
题型五、比较代数式大小
例13、 设,当时,试比较A与B的值的大小。
分析: 方法一:先分别求出代数式A与B当时的值,再比较这两个值的大小;这种比较大小的方法叫求值比大小。
方法二:我们知道,
如果,那么; 如果,那么; 如果,那么。
根据上述规律,我们可以先计算(注意合并同类项),再当,时,求代数式的值,于是,根据这个值的符号(正、零或负),就能断定A与B的大小。这种比较大小的方法叫求差比较法
解法一:
解法二:
当时,
原式
点拨:求差比较法不仅体现了一个重要的数学思想,而且使用起来常常比求值比较法更为简便。
例14. 比较与a的大小。
分析:在代数式和a中,都有同一字母a,所以,不论a为何值,都不会影响与a的大小关系,因此,只要分情况讨论b就可以了。
解一:当时,;
当时,;
当时,。
解二、-a=b,所以,当时,-a>0,即;
当时,;
当时,。
点拨:本题分析比大小和做差比较大小时都发现要进行分类讨论,注意分类要既不重复也不遗漏。
四、中考题型分析
题型一:去括号、合并同类项的题
例1、(2006年长春市) 化简的结果是 ( )
(A)0. (B)2. (C). (D).
分析:本题是去括号、合并同类项的基础题,只要按去括号法则运算即可。
解:。=,所以选C
题型二:求值题
例2、(苏州市2006年) 若x=2,则的值是 ( )
(A) (B)1 (C)4 (D)8
分析:本题也是求值题中的基本题,直接代入求值即可。
解:;所以选B。
例3、(张家界市2006年)13.已知,那么:___________.
分析:本题根据已知条件很难求得x和y的值,所以考虑用整体代入法求值。
解:因为,所以
点拨:求代数式值的题型,一般的解题思路是先化简再代入计算求值。但代数式中字母值很难求时考虑用整体代入法。一般整体代入法求值的题目有一定的特征,就是含未知数的部分可以看成一个整体。
题型三:列代数式题
例4(湖北省荆门市二00六年)6.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
(A)a2-b2=(a+b)(a-b). (B)(a+b)2=a2+2ab+b2.
(C)(a-b)2=a2-2ab+b2. (D)a2-b2=(a-b)2.
分析:图(1)阴影部分的面积是a2-b2,图(2)阴影部分的面积是:,由于阴影部分面积相等,所以选A。
解:选A。
题型五 找规律题型
例5、(常德市,2005)找规律:如图,第(1)幅图中有1个菱形,第(2)幅图中有3个菱形,第(3)幅图中有5个菱形,则第(n)幅图中共有___________个菱形。
分析:第(1)幅图中有1个菱形,第(2)幅图中有3个菱形,第(3)幅图中有5个菱形,第(4)幅图中有7个菱形,所以第(n)幅图中有(2n-1)个菱形。
解:有(2n-1)个
第二章单元测试题
一、选择题(本大题共12题,每小题2分,共24分,每小题只有一个正确选项,把正确选项的代号填在题后的括号里)
1.、在下列代数式:中,单项式有( )
(A)3个 (B)4个 (C)5个 (D)6个
2、.在下列代数式:中,多项式有( )(A)2个 (B)3个 (C)4个 (D)5个
为( )
A. 2 B. 3 C. 4 D. 5
4、. 下列说法中正确的是( )
A. 5不是单项式
5.
A. x与y的一半的差 B. x与y的差的一半 C. x减去y除以2的差
7. 下列各组中,当n=3时是同类项的是( )
8、下列整式加减正确的是【 】
(A)2x-(x2+2x)=-x2 (B)2x-(x2-2x)=x2
(C)2x+(y+2x)=y (D)2x-(x2-2x)=x2
9、减去-2x后,等于4x2-3x-5的代数式是【 】
(A)4x2-5x-5 (B)-4x2+5x+5 (C)4x2-x-5 (D)4x2-5
10.、一个多项式加上3x2y-3xy2得x3-3x2y,这个多项式是【 】
(A)x3+3xy2 (B)x3-3xy2 (C)x3-6x2y+3xy2 (D)x3-6x2y-3xy2
11、. 把,正确的是( )
A. B. C. HYPERLINK "http://www.1230.org" EMBED Equation.2 D.
12、(安徽省,2005)今天,和你一起参加全省课改实验区初中毕业学业考试的同学约有15万人,其中男生约有a万人,则女生约有( )
A、(15+a)万人 B、(15-a)万人 C、15a万人 D、万人
二、填空题(本题共8小题,每小题3分,共24分)
13. 一个三位数,它的个位数字是0,十位数字是a,百位数字是b,用代数式表示这个三位数是__________。
14.若单项式-2x3yn-3是一个关于x,y的5次单项式,则n=_________.
15.若多项式(m+2)y2-3xy3是五次二项式,则m=___________.
16.化简2x-(5a-7x-2a)=__________。
17、. 当时,代数式的值是____________。
18、 已知,则代数式____________。
19、 已知,则代数式____________。
20、 已知长方形的长为a,面积是16,它的宽为________。
三、解答题:(21、22、23、25、26、27每题8分,24题6分)
21、. 补入下列各多项式的缺项,并按x的升幂排列:
(1)-x3+x-2 (2)x4-5-x2 (3)x3-1 (4)1-x4
22、比较下列各式的大小:
(1)比较和的大小。(2) 比较与的大小
23、.
24、已知长方形ABCD中,AB=4cm,AD=2cm,以AB为直径作一个半圆,求阴影部分面积。
26、
27、. 某移动通讯公司开设了两种通讯业务:①“全球通”用户先交50元月租费,然后每通话一分钟,付话费0.6元(市内通话);②“快捷通”,用户不交月租费,每通话一分钟,付话费0.8元(市内通话)。
(1)按一个月通话x分钟计,请你写出两种收费方式下客户应支付的费用;
(2)某用户一个月内市内通话时间为200分钟,选择哪种通讯业务较省钱?
答案:
1、 选择题:
1、 B;分析:数与字母的积叫单项式,单独一个字母或数也是单项式。所以 是单项式,故选B。点拨:注意单项式的定义,代数式中只有数与字母的积,单独一个数字和字母也是单项式。
2、B;分析:几个单项式的和是多项式,要注意分别是一个常数,所以这两个都是单项式;多项式是:,故选B。点拨:由于单独一个数和字母也是单项式,所以是单项式而不是多项式。
3. B ;分析:多项式为八次四项式,就是说有四项,最高次项是八,所以2m+1=7,m=3,所以选B。点拨:多项式的次数是多项式中次数最高项的次数,所以要把每一项的次数都算出来,本题字母是a和b,m是常数,所以只有这一项的次数可能是八次。
4、C。 分析:单项式和多项式统称整式,数与字母的积叫单项式,数字因数叫单项式的系数,所以5是单项式,,,只有。故选C。点拨:单项式和多项式统称整式,而单项式和多项式中只有加、减、乘的运算,当分母中含有字母时一定有除法运算,所以分母中含有字母的代数式决不是整式。
5. B;分析: HYPERLINK "http://www.1230.org" EMBED Equation.2 点拨:根据一些语句列代数式,或根据代数式说出代数式的意义,都要求我们要注意描述运算的关联词。
6. A ;分析:去括号合并同类项就可得结果。点拨:注意第二个括号前是-2,表示-2与括号中的每一项相乘,再把所得的积相加。
7. D ;分析:把n=3代入每一个答案中看相同字母的指数是否相同,如果相同字母的指数也相同就是同类项。点拨:本题也可以一个答案一个答案的看,如果是同类项那么n应该取什么值,看哪个n取3就选哪个,不过这个方法不如第一个方法简单。
8、A;分析:把每个答案去括号合并同类项,看是否等于右边。点拨:注意去括号法则,括号前面是负号,把负号和括号去掉,括号中的每一项都要改变符号。
9、A;分析:设所求代数式为A,则有:A-(-2x)=4x2-3x-5,所以A=4x2-3x-5+(-2x)=4x2-3x-5-2x=4x2-5x-5,所以选A。点拨:已知差和减数,求被减数用加法,被减数=差+减数。所以所求代数式是差的代数式加上减去的代数式。
10、C;分析:设所求代数式为A,则有A+3x2y-3xy2=x3-3x2y,所以A=x3-3x2y-(3x2y-3xy2)=x3-3x2y-3x2y+3xy2=x3-6x2y+3xy2,所以选C。点拨:已知和和其中一个加数,求另一个加数用减法,另一个加数=和-其中一个加数。
11、D。 分析:注意字母换成数,运算顺序和符号不变,所以选D。点拨:代入求值要把代数式的含义搞清楚,要理解代数式中的运算。
12、 B;分析:参加全省课改实验区初中毕业学业考试的学生人数=男生人数+女生人数,所以女生人数=总人数-男生人数。点拨:多项式后面跟单位,要给多项式加括号。
二、填空题
13. ;分析:三位数=百位数字×100+十位数字×10+个位数字;点拨:三位数的表示方法不是abc,这样写的abc式相乘的关系,不表示三位数,所以三位数=百位数字×100+十位数字×10+个位数字。
14、n=5;分析:单项式的次数是所有字母的指数和,因为单项式-2x3yn-3是一个关于x,y的5次单项式,所以3+n-3=5,n=5。点拨:单项式的次数是所有字母的指数和,当已知单项式次数时,可根据单项式的次数列方程,从而求出字母指数的值。
15、;分析:多项式(m+2)y2-3xy3是五次二项式,所以;点拨:多项式的次数是多项式中次数最高项的次数,所以可得方程:到这里考虑平方为4的数有几个?因为,所以。
16、11x-3a;解析:2x-(5a-7x-2a)=2x-5a+7x+2a=11x-3a;点拨:去括号合并同类项时要注意括号前是负号,把括号和负号去掉,括号中的每一项都要变号。
17、;分析:因为,所以=;点拨:把字母的值代入代数式中,代数式所表示的运算不变,即注意字母换成数,运算顺序和符号不变。
18、 ,解析:因为,它的倒数,所以;点拨:所给的已知条件很难求出a与b的值,观察代数式中出现a、b的地方都有一定的特点,所以考虑用整体代入法求值。
19、73;解析: (8x+8y)+5xy=8(x+y)+5xy=8×+5×()=124-51=73。点拨:所给的已知条件无法求出x与y的值,所以考虑将代数式变形整体代入求值。
20、;分析:长方形的面积=长×宽,所以,宽=面积÷长。点拨:除法要写成分数的形式。
三:解答题
21、 解:(1)-2+x+0x2-x3
(2)-5+0x-x2+0x3+x4
(3)-1+0x+0x2+x3
(4)1+0x+0x2+0x3-x4
点拨:补缺项,要先确定现在有哪些项,再观察缺哪些项。因为不能改变多项式的值,所以只能让补入的项系数为0,例如(1)x3+x-2是三次多项式,按x的升幂排列,把(1)-x3+x-2中的各项填入相应的位置,观察发现缺二次项,于是把0x2填入二次项的位置。
常数项 一次项 二次项 三次项
-2 +x 0x2 -x3
同样道理(2)x4-5-x2是4次多项式,应有5项,把x4-5-x2中各项填入相应的位置,观察发现缺一次项和三次项,于是把0x和0x3填入相应的位置。
常数项 一次项 二次项 三次项 四次项
-5 0x -x2 0x3 x4
同样方法可知(3)缺一次项和二次项,(4)缺一次项,二次项,三次项。
有时按升幂排列,也有时需要按降幂排列,方法是类似的。重新排列时注意各项要连同它前面的符号一起移动。
22、 解:(1)
(2) 解一(分析比较法):当时,;
当时,;
当时,。
解二(求差比较法):
∴当时,;
当时,;
当时,
点拨:比较代数式的大小,常用的方法是求差比较法,有时也用分析法。如果求差以后的结果含有字母,那么需要分类讨论。如(2)的解法一:在和中,完全相同的部分是a,b与-b是不同的,所以只要讨论b与-b的大小关系就可以了。解法二求差得2b,所以要对b进行讨论。
23、解:
点拨:整式的加减运算,要把每个整式看成一个整体,加括号以后再进行运算。
24. 解:阴影部分的面积=长方形面积-半圆的面积,所以,阴影部分的面积=4×2-=,所以阴影部分的面积为。
点拨:观察图形可知阴影部分的面积=长方形面积-半圆的面积,这是列代数式的根据。
25、.若代数式(x2+ax-2y+7)-(bx2-2x+9y-1)的值与字母x的取值无关,求a、b的值。
解:(x2+ax-2y+7)-(bx2-2x+9y-1)=x2+ax-2y+7-bx2+2x-9y+1=,因为代数式的值与x无关,所以1-b=0,b=1;a+2=0,a=-2。
点拨:代数式的值与x无关,即合并同类项后不含x ( http: / / www.1230.org )项,也就是含x项的系数为0。
26、. 解:
点拨:由于已知条件中很难求出a和b的值,所以考虑能否用整体代入法。整理化简代数式,发现可以表示成(a-b)和ab的形式,所以可以把
27、解: (1)“全球通”客户支付的费用为:(50+0.6x)元
“快捷通”客户支付的费用为:0.8x元
(2)把x=200分别代入上面两个代数式,得
因为170>160
所以选择“快捷通”业务较省钱。
点拨:“全球通”客户支付的费用=先交的月租50元+0.6×通话分钟数;“快捷通”,用户支付的费用=0.8×通话分钟数。
丰富的问题情景
代数式
单项式
多项式
整式
同类项
合并同类项
去括号、添括号法则
整式加减法
系数
次数
项
列代数式
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 教案·第 18 页 (共 18 页)
