第六章 平面向量及其应用 复习(2) 学案(含解析)高中数学人教A版(2019)必修 第二册
文档属性
| 名称 | 第六章 平面向量及其应用 复习(2) 学案(含解析)高中数学人教A版(2019)必修 第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 00:00:00 | ||
图片预览




文档简介
第六章 平面向量及其应用 复习(二)
能用正弦定理、余弦定理解决三角形中的边角问题及简单的实际问题.
活动一 构建知识网络
活动二 利用正弦定理、余弦定理求三角形的边长或角度的大小
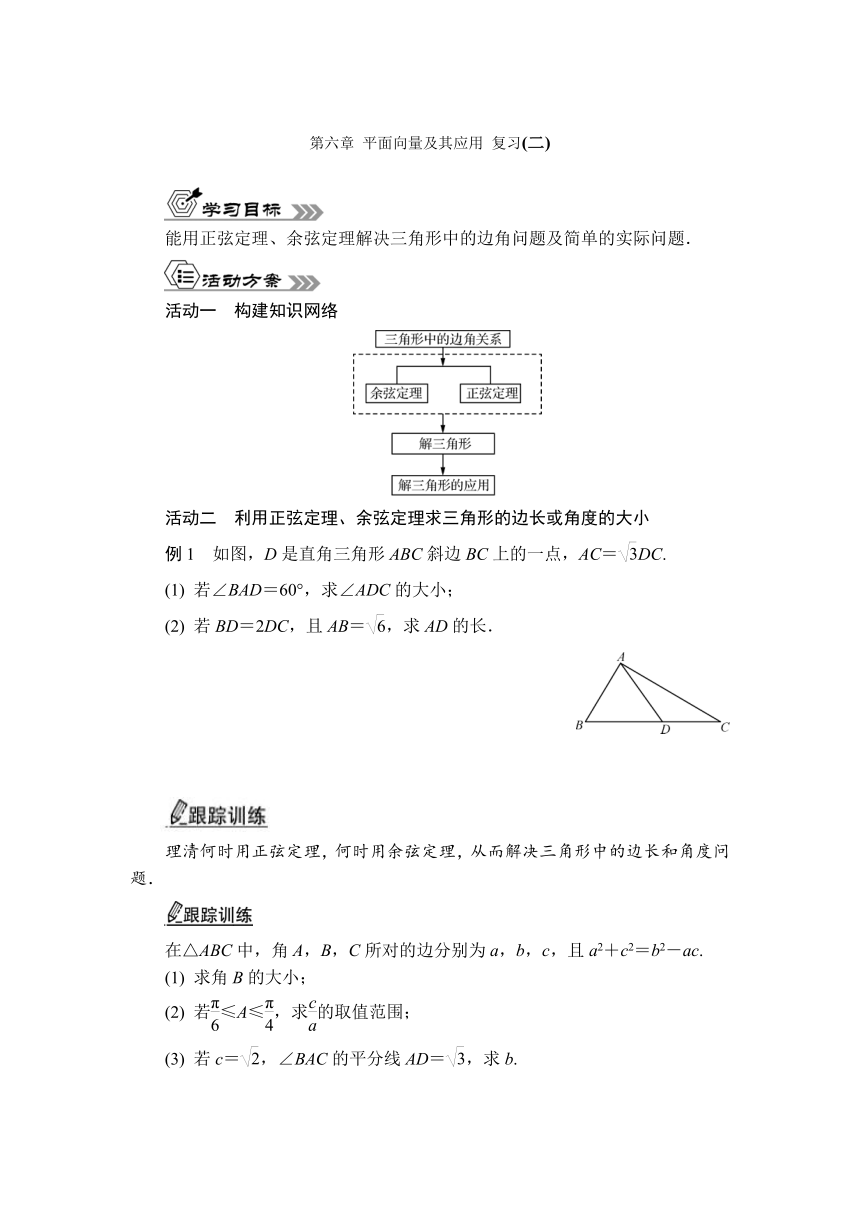
例1 如图,D是直角三角形ABC斜边BC上的一点,AC=DC.
(1) 若∠BAD=60°,求∠ADC的大小;
(2) 若BD=2DC,且AB=,求AD的长.
理清何时用正弦定理,何时用余弦定理,从而解决三角形中的边长和角度问题.
在△ABC中,角A,B,C所对的边分别为a,b,c,且a2+c2=b2-ac.
(1) 求角B的大小;
(2) 若≤A≤,求的取值范围;
(3) 若c=,∠BAC的平分线AD=,求b.
活动三 利用正弦定理求三角形的面积
例2 在△ABC中,角A,B,C所对的边分别是a,b,c,b=,c=1,cos B=.求:
(1) sin C的值;
(2) △ABC的面积.
在△ABC中,a,b,c分别为角A,B,C所对的边长,且c=-3b cos A,tan C=.
(1) 求tan B的值;
(2) 若c=2,求△ABC的面积.
活动四 利用正弦定理、余弦定理解决实际问题
例3 AB是底部为B的建筑物,A是建筑物的最高点,为测量建筑物AB的高度,先将高度为1 m的测角仪放置在CD位置,测得仰角为45°,再将测角仪放置在EF位置,测得仰角为75°,已知DF=2 m,D,F,B在同一水平线上,求建筑物AB的高度.
实际问题中的长度与角度的大小的计算,往往借助于正、余弦定理去解决,只要将所求的长度或角度放在适当的三角形中即可.
如图,已知在东西走向上有AM,BN两座发射塔,且AM=100 m,BN=200 m,一辆测量车在塔底M的正南方向的P处测得发射塔顶A的仰角为30°,该测量车向北偏西60°方向行驶了100 m后到达Q处,在Q处测得发射塔顶B的仰角为θ,且∠BQA=θ,经计算,tan θ=2,求两发射塔顶A,B之间的距离.
1. 在△ABC中,角A,B,C所对的边分别为a,b,c,若a+b=2c,则cos C的最小值为( )
A. - B. C. D.
2. 在△ABC中,角A,B,C所对的边分别为a,b,c.若A=45°,B=60°,a=1,则b的值为( )
A. B. C. D.
3. (多选)(2023三明高一联考)已知在△ABC中,角A,B,C所对的边分别为a,b,c,则下列命题中正确的有( )
A. 当a=5,b=7,A=60°时,满足条件的三角形有1个
B. 若sin A∶sin B∶sin C=3∶5∶7则这个三角形的最大角是120°
C. 若a2+b2>c2,则△ABC为锐角三角形
D. 若C=,a2-c2=bc,则△ABC为等腰直角三角形
4. 在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=90°,∠ABC的平分线交AC于点D,且BD=2,则a+4c的最小值为________.
5. (2023菏泽高一阶段练习)在△ABC中,角A,B,C所对的边分别为a,b,c,且2b cos C=2a+c.
(1) 求角B的大小;
(2) 若b=2,D为AC边上的一点,BD=1,且________,求△ABC的面积.
请在下面两个条件中选择一个作为条件补充在横线上,并解决问题.
①BD是∠ABC的平分线;②D为线段AC的中点.
【答案解析】
第六章 平面向量及其应用 复习(二)
【活动方案】
例1 (1) 因为∠BAD=60°,∠BAC=90°,
所以∠DAC=30°.
在△ADC中,由正弦定理,得=,
则sin ∠ADC=·sin ∠DAC=,
所以∠ADC=120°或∠ADC=60°.
又∠BAD=60°,所以∠ADC=120°.
(2) 因为BD=2DC,所以BC=3DC.
在△ABC中,由勾股定理可得BC2=AB2+AC2,
即9DC2=6+3DC2,解得DC=1,
所以BD=2,AC=.
令∠ADB=θ,
在△ADB中,由余弦定理,
得AB2=AD2+BD2-2AD·BD·cos θ,
在△ADC中,由余弦定理,
得AC2=AD2+CD2-2AD·CD·cos (π-θ),
即
解得AD2=2,故AD=.
跟踪训练 (1) 因为a2+c2=b2-ac,
所以由余弦定理,得cos B==-.
因为0(2) 因为B=,所以A+C=,
所以===-.
又因为≤A≤,所以≤tan A≤1,
所以≤≤1,
所以的取值范围为.
(3) 在△ABD中,AB=,AD=,B=,
由正弦定理,得=,即=,
所以sin ∠ADB=,显然∠ADB=,
所以∠BAD=,
所以∠BAC=,C=.
在△ABC中,C=,B=,c=,
则由正弦定理=,得=,
解得b=.
例2 (1) 因为b=,c=1,cos B=,
所以sin B==,
所以由正弦定理,得sinC===.
(2) 因为c所以由(1)可得cos C==,
所以sinA=sin (B+C)=sin B cos C+cos B sin C=×+×=,
所以S△ABC=bc sin A=××1×=.
跟踪训练 (1) 由正弦定理,得 sin C=-3sin B cos A,
即sin (A+B)=-3sin B cos A,
所以sin A cos B+cos A sin B=-3sin B cos A,
从而sin A cos B=-4sin B cos A.
因为cos A cos B≠0,所以=-4.
又tan C=-tan (A+B)==,
所以=,
解得tanB=.
(2) 由(1),得 sin A=,sin B=,sin C=.
由正弦定理,得a===,
所以△ABC的面积为ac sin B=××2×=.
例3 在△ACE中,=,
AE===2(m),
AB=AG+1=AE sin 75°+1=2×+1=2+(m),
所以建筑物AB的高度为(2+)m.
跟踪训练 在Rt△AMP中,∠APM=30°,AM=100 m,
所以PM=100 m.
连接QM.
在△PQM中,∠QPM=60°,PQ=100 m,
所以△PQM为等边三角形,所以QM=100 m,
所以在Rt△AMQ中,得AQ=200 m.
在Rt△BNQ中,因为tan θ=2,BN=200 m,
所以QN=100 m,BQ=100 m,cos θ=.
在△BQA中,由余弦定理,得BA2=BQ2+AQ2-2BQ·AQ cos θ,
所以BA=100 m,
所以两发射塔顶A,B之间的距离是100 m.
【检测反馈】
1. B 解析:由余弦定理,得cos C===≥=,当且仅当a=b时等号成立.
2. D 解析:因为=,所以b==1××=.
3. BD 解析:对于A,sin B===>1,无解,故A错误;对于B,由sin A∶sin B∶sin C=3∶5∶7,得a∶b∶c=3∶5∶7,不妨令a=3,则b=5,c=7,最大角C的余弦值为cos C===-,所以C=120°,故B正确;对于C,由条件,结合余弦定理只能得到cos C>0,即角C为锐角,无法保证其他角也为锐角,故C错误;对于D,由cos C====cos =,得b+c=a,所以a2=bc+c2=c(b+c)=ac,所以a=c,所以sin A=sin C=sin =1,所以A=,所以△ABC为等腰直角三角形,故D正确.故选BD.
4. 18 解析:根据题意,得S△ABC=ac.因为∠ABC的平分线交AC于点D,且BD=2,所以S△ABD=·BD·c·sin ∠ABD=c,S△CBD=BD·a·sin ∠CBD=a.又S△ABC=S△ABD+S△CBD,所以ac=c+a,化简,得+=1,则a+4c=(a+4c)·=10++≥10+2=18,当且仅当a=2c,即c=3,a=6时取等号,即a+4c的最小值为18.
5. (1) 由题意,及正弦定理,得2sin B cos C=2sin A+sin C=2sin B cos C+2cos B sin C+sin C,
所以2cos B sin C+sin C=0.
因为C∈(0,π),
所以sin C>0,cos B=-.
因为B∈(0,π),所以B=.
(2) 若选①:
由BD平分∠ABC,得S△ABC=S△ABD+S△BCD,
所以ac sin =×1×c sin +×1×a sin ,
即ac=a+c.
在△ABC中,由余弦定理,得b2=a2+c2-2ac cos ,
又b=2,所以a2+c2+ac=12,
联立得(ac)2-ac-12=0,
解得ac=4,
所以S△ABC=ac sin =×4×=.
若选②:
因为=(+),
所以||2=(+)2=(||2+2·+||2),
即1=(c2+2ac cos +a2),则a2+c2-ac=4,
在△ABC中,由余弦定理,得b2=a2+c2-2ac cos ,
又b=2,所以a2+c2+ac=12,
联立解得ac=4,
所以S△ABC=ac sin =×4×=.
能用正弦定理、余弦定理解决三角形中的边角问题及简单的实际问题.
活动一 构建知识网络
活动二 利用正弦定理、余弦定理求三角形的边长或角度的大小
例1 如图,D是直角三角形ABC斜边BC上的一点,AC=DC.
(1) 若∠BAD=60°,求∠ADC的大小;
(2) 若BD=2DC,且AB=,求AD的长.
理清何时用正弦定理,何时用余弦定理,从而解决三角形中的边长和角度问题.
在△ABC中,角A,B,C所对的边分别为a,b,c,且a2+c2=b2-ac.
(1) 求角B的大小;
(2) 若≤A≤,求的取值范围;
(3) 若c=,∠BAC的平分线AD=,求b.
活动三 利用正弦定理求三角形的面积
例2 在△ABC中,角A,B,C所对的边分别是a,b,c,b=,c=1,cos B=.求:
(1) sin C的值;
(2) △ABC的面积.
在△ABC中,a,b,c分别为角A,B,C所对的边长,且c=-3b cos A,tan C=.
(1) 求tan B的值;
(2) 若c=2,求△ABC的面积.
活动四 利用正弦定理、余弦定理解决实际问题
例3 AB是底部为B的建筑物,A是建筑物的最高点,为测量建筑物AB的高度,先将高度为1 m的测角仪放置在CD位置,测得仰角为45°,再将测角仪放置在EF位置,测得仰角为75°,已知DF=2 m,D,F,B在同一水平线上,求建筑物AB的高度.
实际问题中的长度与角度的大小的计算,往往借助于正、余弦定理去解决,只要将所求的长度或角度放在适当的三角形中即可.
如图,已知在东西走向上有AM,BN两座发射塔,且AM=100 m,BN=200 m,一辆测量车在塔底M的正南方向的P处测得发射塔顶A的仰角为30°,该测量车向北偏西60°方向行驶了100 m后到达Q处,在Q处测得发射塔顶B的仰角为θ,且∠BQA=θ,经计算,tan θ=2,求两发射塔顶A,B之间的距离.
1. 在△ABC中,角A,B,C所对的边分别为a,b,c,若a+b=2c,则cos C的最小值为( )
A. - B. C. D.
2. 在△ABC中,角A,B,C所对的边分别为a,b,c.若A=45°,B=60°,a=1,则b的值为( )
A. B. C. D.
3. (多选)(2023三明高一联考)已知在△ABC中,角A,B,C所对的边分别为a,b,c,则下列命题中正确的有( )
A. 当a=5,b=7,A=60°时,满足条件的三角形有1个
B. 若sin A∶sin B∶sin C=3∶5∶7则这个三角形的最大角是120°
C. 若a2+b2>c2,则△ABC为锐角三角形
D. 若C=,a2-c2=bc,则△ABC为等腰直角三角形
4. 在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=90°,∠ABC的平分线交AC于点D,且BD=2,则a+4c的最小值为________.
5. (2023菏泽高一阶段练习)在△ABC中,角A,B,C所对的边分别为a,b,c,且2b cos C=2a+c.
(1) 求角B的大小;
(2) 若b=2,D为AC边上的一点,BD=1,且________,求△ABC的面积.
请在下面两个条件中选择一个作为条件补充在横线上,并解决问题.
①BD是∠ABC的平分线;②D为线段AC的中点.
【答案解析】
第六章 平面向量及其应用 复习(二)
【活动方案】
例1 (1) 因为∠BAD=60°,∠BAC=90°,
所以∠DAC=30°.
在△ADC中,由正弦定理,得=,
则sin ∠ADC=·sin ∠DAC=,
所以∠ADC=120°或∠ADC=60°.
又∠BAD=60°,所以∠ADC=120°.
(2) 因为BD=2DC,所以BC=3DC.
在△ABC中,由勾股定理可得BC2=AB2+AC2,
即9DC2=6+3DC2,解得DC=1,
所以BD=2,AC=.
令∠ADB=θ,
在△ADB中,由余弦定理,
得AB2=AD2+BD2-2AD·BD·cos θ,
在△ADC中,由余弦定理,
得AC2=AD2+CD2-2AD·CD·cos (π-θ),
即
解得AD2=2,故AD=.
跟踪训练 (1) 因为a2+c2=b2-ac,
所以由余弦定理,得cos B==-.
因为0
所以===-.
又因为≤A≤,所以≤tan A≤1,
所以≤≤1,
所以的取值范围为.
(3) 在△ABD中,AB=,AD=,B=,
由正弦定理,得=,即=,
所以sin ∠ADB=,显然∠ADB=,
所以∠BAD=,
所以∠BAC=,C=.
在△ABC中,C=,B=,c=,
则由正弦定理=,得=,
解得b=.
例2 (1) 因为b=,c=1,cos B=,
所以sin B==,
所以由正弦定理,得sinC===.
(2) 因为c
所以sinA=sin (B+C)=sin B cos C+cos B sin C=×+×=,
所以S△ABC=bc sin A=××1×=.
跟踪训练 (1) 由正弦定理,得 sin C=-3sin B cos A,
即sin (A+B)=-3sin B cos A,
所以sin A cos B+cos A sin B=-3sin B cos A,
从而sin A cos B=-4sin B cos A.
因为cos A cos B≠0,所以=-4.
又tan C=-tan (A+B)==,
所以=,
解得tanB=.
(2) 由(1),得 sin A=,sin B=,sin C=.
由正弦定理,得a===,
所以△ABC的面积为ac sin B=××2×=.
例3 在△ACE中,=,
AE===2(m),
AB=AG+1=AE sin 75°+1=2×+1=2+(m),
所以建筑物AB的高度为(2+)m.
跟踪训练 在Rt△AMP中,∠APM=30°,AM=100 m,
所以PM=100 m.
连接QM.
在△PQM中,∠QPM=60°,PQ=100 m,
所以△PQM为等边三角形,所以QM=100 m,
所以在Rt△AMQ中,得AQ=200 m.
在Rt△BNQ中,因为tan θ=2,BN=200 m,
所以QN=100 m,BQ=100 m,cos θ=.
在△BQA中,由余弦定理,得BA2=BQ2+AQ2-2BQ·AQ cos θ,
所以BA=100 m,
所以两发射塔顶A,B之间的距离是100 m.
【检测反馈】
1. B 解析:由余弦定理,得cos C===≥=,当且仅当a=b时等号成立.
2. D 解析:因为=,所以b==1××=.
3. BD 解析:对于A,sin B===>1,无解,故A错误;对于B,由sin A∶sin B∶sin C=3∶5∶7,得a∶b∶c=3∶5∶7,不妨令a=3,则b=5,c=7,最大角C的余弦值为cos C===-,所以C=120°,故B正确;对于C,由条件,结合余弦定理只能得到cos C>0,即角C为锐角,无法保证其他角也为锐角,故C错误;对于D,由cos C====cos =,得b+c=a,所以a2=bc+c2=c(b+c)=ac,所以a=c,所以sin A=sin C=sin =1,所以A=,所以△ABC为等腰直角三角形,故D正确.故选BD.
4. 18 解析:根据题意,得S△ABC=ac.因为∠ABC的平分线交AC于点D,且BD=2,所以S△ABD=·BD·c·sin ∠ABD=c,S△CBD=BD·a·sin ∠CBD=a.又S△ABC=S△ABD+S△CBD,所以ac=c+a,化简,得+=1,则a+4c=(a+4c)·=10++≥10+2=18,当且仅当a=2c,即c=3,a=6时取等号,即a+4c的最小值为18.
5. (1) 由题意,及正弦定理,得2sin B cos C=2sin A+sin C=2sin B cos C+2cos B sin C+sin C,
所以2cos B sin C+sin C=0.
因为C∈(0,π),
所以sin C>0,cos B=-.
因为B∈(0,π),所以B=.
(2) 若选①:
由BD平分∠ABC,得S△ABC=S△ABD+S△BCD,
所以ac sin =×1×c sin +×1×a sin ,
即ac=a+c.
在△ABC中,由余弦定理,得b2=a2+c2-2ac cos ,
又b=2,所以a2+c2+ac=12,
联立得(ac)2-ac-12=0,
解得ac=4,
所以S△ABC=ac sin =×4×=.
若选②:
因为=(+),
所以||2=(+)2=(||2+2·+||2),
即1=(c2+2ac cos +a2),则a2+c2-ac=4,
在△ABC中,由余弦定理,得b2=a2+c2-2ac cos ,
又b=2,所以a2+c2+ac=12,
联立解得ac=4,
所以S△ABC=ac sin =×4×=.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
