2.4.2圆的一般方程 课件(共13张PPT)
文档属性
| 名称 | 2.4.2圆的一般方程 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
2.4.2
圆的一般方程
圆的标准方程:
(x-a)2+(y-b)2=r2
特征:直接看出圆心与半径
把圆的标准方程(x-a)2+(y-b)2=r2
展开,得
-
2
2
2
2
2
2
0
2
=
-
+
+
-
+
r
b
a
by
ax
y
x
D
E
F
x2 +y 2+Dx+Ey+F=0
结论:任何一个圆方程可以写成下面形式
00 复习
1.是不是任何一个形如 x2 +y 2+Dx+Ey+F=0方程都表示的曲线是圆呢?
2.下列方程表示什么图形?
(1)x2+y2-2x+4y+1=0;
(2)x2+y2-2x-4y+5 =0;
(3)x2+y2-2x+4y+6=0.
01 圆的一般方程
思考:
将 x2 +y 2+Dx+Ey+F=0 左边配方,得
(1)当
时,
它表示以
为圆心,
以
为半径的圆;
D2+E2-4F>0
(2)当D2+E2-4F=0时,方程表示点 ;
(3)当D2+E2-4F<0时,方程无实数解,不表示任何图形.
01 圆的一般方程
圆的一般方程与圆的标准方程的联系:
一般方程
标准方程
x2 +y 2+Dx+Ey+F=0
(x-a)2+(y-b)2=r2
(D2+E2-4F>0)
01 圆的一般方程
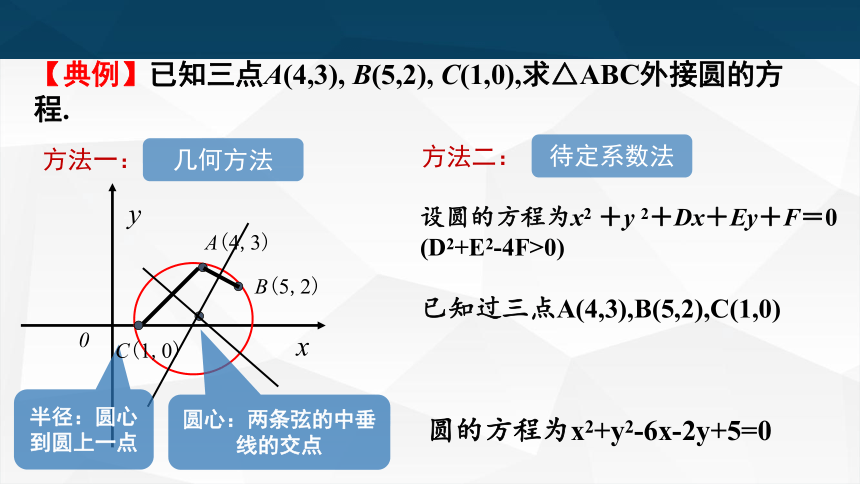
几何方法
方法一:
y
x
A(4,3)
B(5,2)
0
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
【典例】已知三点A(4,3), B(5,2), C(1,0),求△ABC外接圆的方程.
C(1,0)
待定系数法
方法二:
设圆的方程为x2 +y 2+Dx+Ey+F=0 (D2+E2-4F>0)
已知过三点A(4,3),B(5,2),C(1,0)
圆的方程为x2+y2-6x-2y+5=0
求轨迹方程
(直接法)
【典例】已知圆x2+y2=1,点A(1,0),△ABC内接于圆,且∠BAC=60°,当B,C在圆上运动时,BC中点D的轨迹方程是 ( )
x
y
O
A
B
C
A.x2+y2=
B.x2+y2=
C.x2+y2=
D.x2+y2=
x
y
O
A
B
C
求轨迹方程
【典例】已知线段AB的端点B坐标是(4,3),端点A在圆(x+1)2+y2 =4上移动,求线段AB的中点的轨迹方程。
求轨迹方程
x
y
O
(x,y)
(4,3)
练习 已知动点A在圆x2+y2 =1上移动,点B(3,0),则AB的中点的轨迹方程是( )
A.(x+3)2+y2=4 B.(x-3)2+y2=1
C. +y2= D. +y2=
x
y
O
(x,y)
(3,0)
(代入法)
“过圆x2+y2 =9上的点A作x轴的垂线,垂足为C,点P在线段AC上,且2|AP|=|PC|”,求点P的轨迹方程.
x
y
O
(x,y)
C(x,0)
求轨迹方程
(代入法)
已知y=kx+1与圆x2+y2=4相交于A, B两点,以OA,OB为邻边构成平行四边形OAPB,求P点的轨迹方程.
求轨迹方程
“过点A作x轴的垂线,垂足为C,点P在线段AC上,且2|AP|=|PC|”,求点P的轨迹方程.
x
y
O
(x,y)
C(x,0)
【习练·破】
长度为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,则线段AB的中点M的轨迹方程为________.
求轨迹方程
2.4.2
圆的一般方程
圆的标准方程:
(x-a)2+(y-b)2=r2
特征:直接看出圆心与半径
把圆的标准方程(x-a)2+(y-b)2=r2
展开,得
-
2
2
2
2
2
2
0
2
=
-
+
+
-
+
r
b
a
by
ax
y
x
D
E
F
x2 +y 2+Dx+Ey+F=0
结论:任何一个圆方程可以写成下面形式
00 复习
1.是不是任何一个形如 x2 +y 2+Dx+Ey+F=0方程都表示的曲线是圆呢?
2.下列方程表示什么图形?
(1)x2+y2-2x+4y+1=0;
(2)x2+y2-2x-4y+5 =0;
(3)x2+y2-2x+4y+6=0.
01 圆的一般方程
思考:
将 x2 +y 2+Dx+Ey+F=0 左边配方,得
(1)当
时,
它表示以
为圆心,
以
为半径的圆;
D2+E2-4F>0
(2)当D2+E2-4F=0时,方程表示点 ;
(3)当D2+E2-4F<0时,方程无实数解,不表示任何图形.
01 圆的一般方程
圆的一般方程与圆的标准方程的联系:
一般方程
标准方程
x2 +y 2+Dx+Ey+F=0
(x-a)2+(y-b)2=r2
(D2+E2-4F>0)
01 圆的一般方程
几何方法
方法一:
y
x
A(4,3)
B(5,2)
0
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
【典例】已知三点A(4,3), B(5,2), C(1,0),求△ABC外接圆的方程.
C(1,0)
待定系数法
方法二:
设圆的方程为x2 +y 2+Dx+Ey+F=0 (D2+E2-4F>0)
已知过三点A(4,3),B(5,2),C(1,0)
圆的方程为x2+y2-6x-2y+5=0
求轨迹方程
(直接法)
【典例】已知圆x2+y2=1,点A(1,0),△ABC内接于圆,且∠BAC=60°,当B,C在圆上运动时,BC中点D的轨迹方程是 ( )
x
y
O
A
B
C
A.x2+y2=
B.x2+y2=
C.x2+y2=
D.x2+y2=
x
y
O
A
B
C
求轨迹方程
【典例】已知线段AB的端点B坐标是(4,3),端点A在圆(x+1)2+y2 =4上移动,求线段AB的中点的轨迹方程。
求轨迹方程
x
y
O
(x,y)
(4,3)
练习 已知动点A在圆x2+y2 =1上移动,点B(3,0),则AB的中点的轨迹方程是( )
A.(x+3)2+y2=4 B.(x-3)2+y2=1
C. +y2= D. +y2=
x
y
O
(x,y)
(3,0)
(代入法)
“过圆x2+y2 =9上的点A作x轴的垂线,垂足为C,点P在线段AC上,且2|AP|=|PC|”,求点P的轨迹方程.
x
y
O
(x,y)
C(x,0)
求轨迹方程
(代入法)
已知y=kx+1与圆x2+y2=4相交于A, B两点,以OA,OB为邻边构成平行四边形OAPB,求P点的轨迹方程.
求轨迹方程
“过点A作x轴的垂线,垂足为C,点P在线段AC上,且2|AP|=|PC|”,求点P的轨迹方程.
x
y
O
(x,y)
C(x,0)
【习练·破】
长度为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,则线段AB的中点M的轨迹方程为________.
求轨迹方程
