华师大版数学九年级上册 导学案:24.2《直角三角形的性质》(无答案)
文档属性
| 名称 | 华师大版数学九年级上册 导学案:24.2《直角三角形的性质》(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 15.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-11 11:26:16 | ||
图片预览

文档简介
课题
直角三角形的性质
课型
班级
姓名
时间
课堂
流程
环节
具 体 内 容
学法
指导
时间
课堂实录
与反思
学习
目标
1、掌握“直角三角形的两个锐角互余”的定理.
2、巩固利用添辅助线证明有关几何问题的方法.
3、掌握“直角三角形斜边上的中线等于斜边的一半”定理以及应用.
温故知新
三角形的分类?
2、三角形的内角和定理是什么?
3、直角三角形是一类特殊的三角形,
除了具备三角形的性质外,还具备哪些性质?
自学
自研
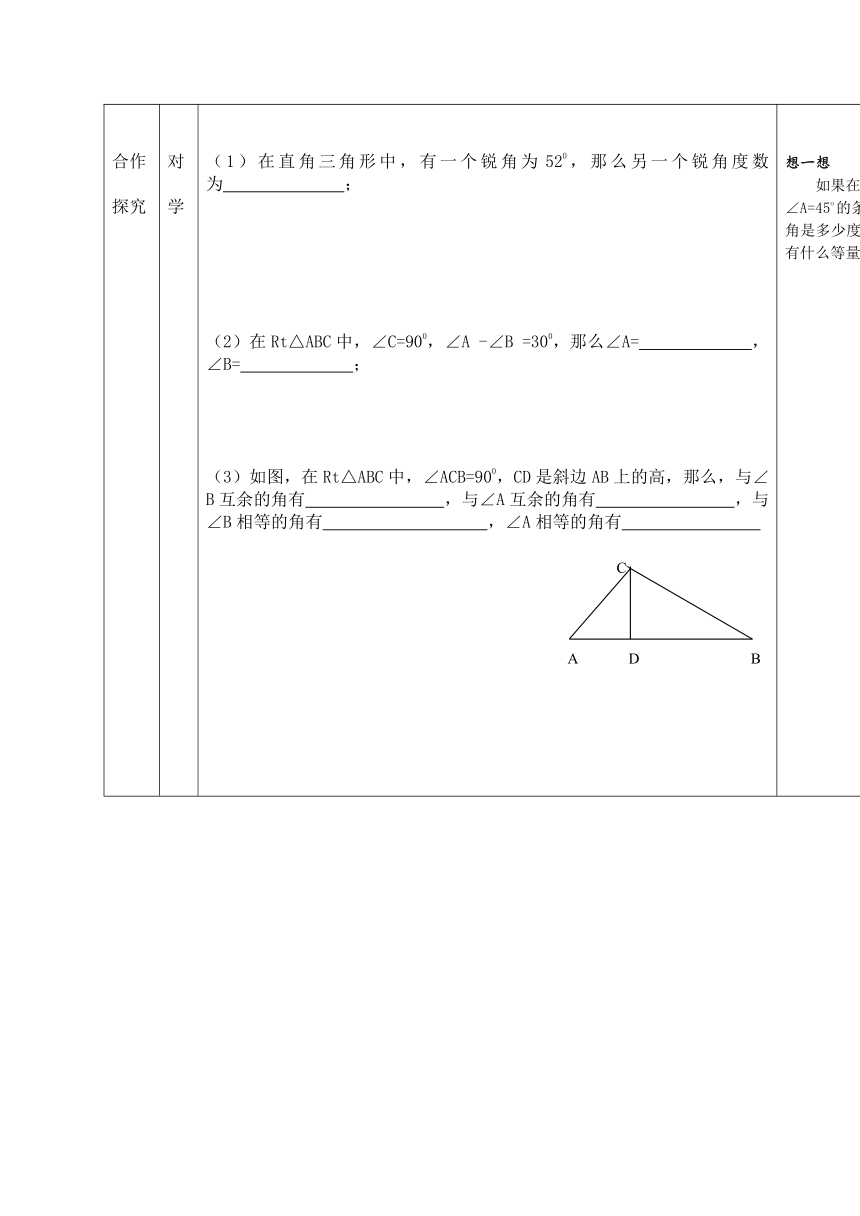
(1)研究直角三角形性质定理一
如图:∠A与∠B有何关系?为什么?
归纳:定理1:
合作
探究
对
学
(1)在直角三角形中,有一个锐角为520,那么另一个锐角度数为???????;
(2)在Rt△ABC中,∠C=900,∠A -∠B =300,那么∠A=?????? ,∠B=?????? ;
(3)如图,在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,那么,与∠B互余的角有????????,与∠A互余的角有????????,与∠B相等的角有????????? ,∠A相等的角有????????
想一想
如果在练习(3)中添加∠A=45o的条件,那么各个锐角是多少度?各个线段之间有什么等量关系?
展示
质疑
点拨
提升
群学
猜一猜 量一量
CD= ;AD=
BD= ;AB= ;
CD= AB
猜想:直角三角形斜边上的中线等于斜边的一半吗?
证一证
命题:直角三角形斜边上的中线等于斜边的一半.
已知:在Rt△ABC中,∠ACB=900,CD是斜边AB的中线.
求证:CD=AB(论证过程参照书本)
归纳总结:
定理2:
例1:如果三角形一边上的中线等于这条边的一半,求证:这个三角形是直角三角形。
已知:如图,CD是△ABC的AB边上的中线,且CD=AB。
求证:△ABC是直角三角形。
想一想让学生通过等腰直角三角形这个特殊的直角三角形的斜边上中线与斜边的等量关系的研究,转入到对任意直角三角形斜边上的中线与斜边的等量关系的思考。
疏理
巩固
【课堂小结】
1、这节课主要讲了直角三角形的那两条性质定理?
2、在解决具体问题中你有哪些收获?
活力
冲关
在△ABC中, ∠ACB=90 °,CE是AB边上的中线,那么与CE相等的线段有_________,与∠A相等的角有________,
若∠A=35°,那么∠ECB= _________.
3、在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________.
4、例题:如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且DE=DF.
求证:AB=AC
直角三角形的性质
课型
班级
姓名
时间
课堂
流程
环节
具 体 内 容
学法
指导
时间
课堂实录
与反思
学习
目标
1、掌握“直角三角形的两个锐角互余”的定理.
2、巩固利用添辅助线证明有关几何问题的方法.
3、掌握“直角三角形斜边上的中线等于斜边的一半”定理以及应用.
温故知新
三角形的分类?
2、三角形的内角和定理是什么?
3、直角三角形是一类特殊的三角形,
除了具备三角形的性质外,还具备哪些性质?
自学
自研
(1)研究直角三角形性质定理一
如图:∠A与∠B有何关系?为什么?
归纳:定理1:
合作
探究
对
学
(1)在直角三角形中,有一个锐角为520,那么另一个锐角度数为???????;
(2)在Rt△ABC中,∠C=900,∠A -∠B =300,那么∠A=?????? ,∠B=?????? ;
(3)如图,在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,那么,与∠B互余的角有????????,与∠A互余的角有????????,与∠B相等的角有????????? ,∠A相等的角有????????
想一想
如果在练习(3)中添加∠A=45o的条件,那么各个锐角是多少度?各个线段之间有什么等量关系?
展示
质疑
点拨
提升
群学
猜一猜 量一量
CD= ;AD=
BD= ;AB= ;
CD= AB
猜想:直角三角形斜边上的中线等于斜边的一半吗?
证一证
命题:直角三角形斜边上的中线等于斜边的一半.
已知:在Rt△ABC中,∠ACB=900,CD是斜边AB的中线.
求证:CD=AB(论证过程参照书本)
归纳总结:
定理2:
例1:如果三角形一边上的中线等于这条边的一半,求证:这个三角形是直角三角形。
已知:如图,CD是△ABC的AB边上的中线,且CD=AB。
求证:△ABC是直角三角形。
想一想让学生通过等腰直角三角形这个特殊的直角三角形的斜边上中线与斜边的等量关系的研究,转入到对任意直角三角形斜边上的中线与斜边的等量关系的思考。
疏理
巩固
【课堂小结】
1、这节课主要讲了直角三角形的那两条性质定理?
2、在解决具体问题中你有哪些收获?
活力
冲关
在△ABC中, ∠ACB=90 °,CE是AB边上的中线,那么与CE相等的线段有_________,与∠A相等的角有________,
若∠A=35°,那么∠ECB= _________.
3、在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________.
4、例题:如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且DE=DF.
求证:AB=AC
