5.3简单的轴对称图形第1课时(教学课件)-七年级数学下册同步课件(北师大版)
文档属性
| 名称 | 5.3简单的轴对称图形第1课时(教学课件)-七年级数学下册同步课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 869.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
第1课时
北师大版 数学 七年级下册
3 简单的轴对称图形
第五章 生活中的轴对称
学习目标
1.理解并掌握等腰三角形的性质;(重点)
2.探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.(难点)
一、导入新课
复习回顾
1.轴对称的性质:
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴
,对应线段 ,对应角 .
垂直平分
相等
相等
2.画轴对称图形:
(1)找:找 ;
(2)作:作关键点的 ;
(3)连:按已知图形的方式连接各关键点的对应点.
关键点
对应点
观察下列图片,它们有什么共同的特征?
一、导入新课
情境导入
等腰三角形是生活中常见的图形,它有什么特征 下面我们一起来探究!
二、新知探究
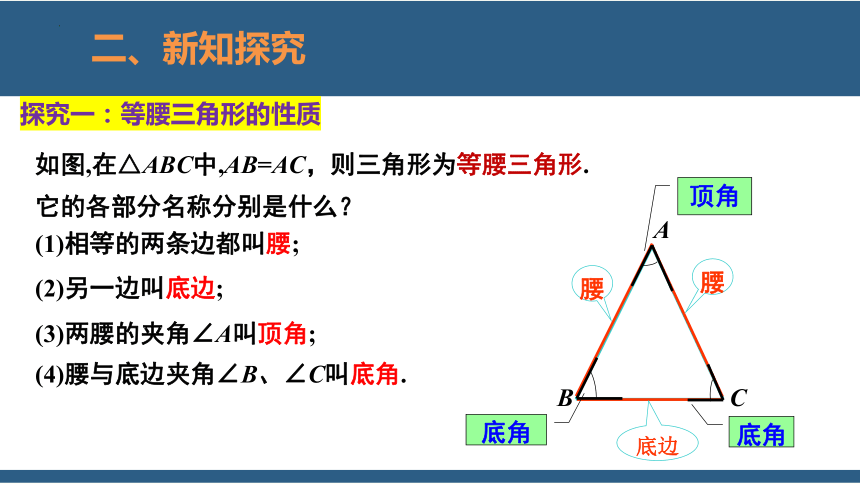
探究一:等腰三角形的性质
如图,在△ABC中,AB=AC,则三角形为等腰三角形.
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫腰;
腰
腰
底边
(2)另一边叫底边;
顶角
底角
底角
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角.
议一议:(1)等腰三角形是轴对称图形吗 如果是,请找出它的对称轴.
二、新知探究
解:(1)等腰三角形是轴对称图形.
(2)等腰三角形顶角平分线所在的直线是它的对称轴吗
(2)等腰三角形顶角平分线所在的直线是它的对称轴.
如图,将等腰三角形沿过顶点的直线折叠,使得两底角重合,折痕所在的直线即为等腰三角形的对称轴.
二、新知探究
(3)等腰三角形底边上的中线所在的直线是它的对称轴吗 底边上的高所在的直线呢
(4)沿对称轴对折,你能发现等腰三角形的哪些特征 说说你的理由.
(3)都是它的对称轴.
(4)答案不唯一,如等腰三角形的两个底角相等.
二、新知探究
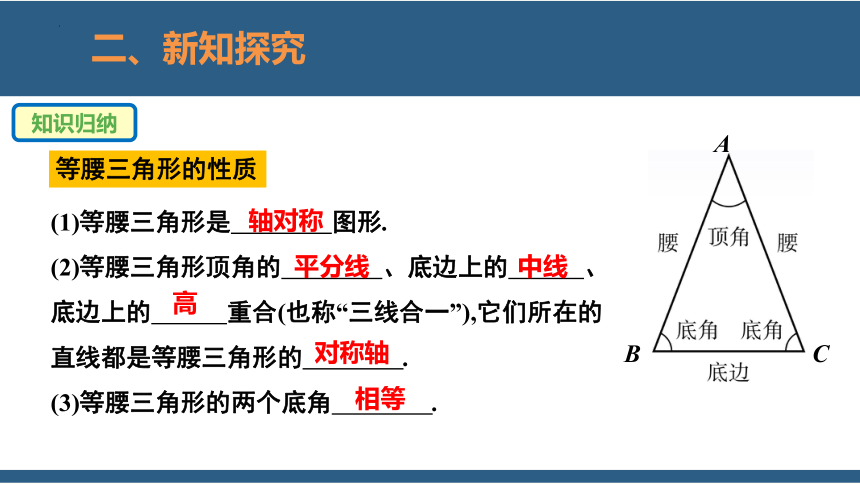
知识归纳
(1)等腰三角形是 图形.
(2)等腰三角形顶角的 、底边上的 、底边上的 重合(也称“三线合一”),它们所在的直线都是等腰三角形的 .
(3)等腰三角形的两个底角 .
轴对称
平分线
中线
高
对称轴
相等
等腰三角形的性质
A
B
C
二、新知探究
跟踪练习
1.等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
A
分类讨论思想.
2.如图所示,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.试说明:∠CBE=∠BAD.
二、新知探究
跟踪练习
解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,AD⊥BC.
又∵BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°,
∴∠CBE=∠CAD,
∴∠CBE=∠BAD.
二、新知探究
(1)等腰三角形“三线合一”的性质是说明角相等、线段相等和垂直关系的既重要又简便的方法;
(2)在等腰三角形中,作“三线”中的“一线”,利用“三线合一”的性质是解决有关等腰三角形问题的常见方法.
方法归纳
想一想: (1)等边三角形有几条对称轴
二、新知探究
探究二:等边三角形的性质
(2)你能发现它的哪些特征
解:(1)等边三角形有3条对称轴.
(2)等边三角形是轴对称图形,三个内角都为60°,三条边都相等.
等边三角形是特殊的等腰三角形,具有等腰三角形的所有的性质.
二、新知探究
(1)等边三角形是轴对称图形,有 条对称轴.
(2)等边三角形每条边都 ,每个角都 ,都等于 .
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合(“三线合一”).
三
相等
相等
60°
知识归纳
等边三角形的性质
A
B
C
3.如图所示,△ABC是等边三角形,D是BC的中点,点E在AC上,且AE=AD,求∠EDC的度数.
二、新知探究
解: 因为△ABC是等边三角形,D是BC的中点,
所以AD⊥BC,∠DAC=30°,
所以∠ADC=90°.
因为AE=AD,
所以∠ADE==75°,
所以∠EDC=∠ADC-∠ADE=90°-75°=15°.
跟踪练习
二、新知探究
议一议:你有哪些办法可以得到一个等腰三角形?与同伴进行交流.
方法:折一折,剪一剪.
把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC是等腰三角形.
A
B
C
展开
例1:如图所示,在△ABC中,AB=AC,AD是BC边上的高,过点C作CE∥AB交AD的延长线于点E.试说明:CE=AB.
三、典例精析
解:因为AB=AC,AD是BC边上的高,
所以BD=CD.
因为CE∥AB,
所以∠E=∠BAE.
在△ABD和△ECD中,
因为∠ADB=∠EDC,∠BAD=∠E,BD=CD,
所以△ABD≌△ECD(AAS).所以CE=AB.
例2:如图所示,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.试说明:∠DBC=∠E.
三、典例精析
解:因为△ABC是等边三角形,
所以∠ABC=∠ACB=60°,AB=BC,
所以∠ACE=120°.
因为D为AC的中点,AB=BC,
因为CE=CD,
所以∠DBC=∠E.
2.如图所示,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30°
C.45° D.60°
四、当堂练习
A
1.下列说法中错误的是( )
A.等腰三角形的两个底角相等
B.等边三角形有一条对称轴
C.等腰三角形底边上的中线平分顶角
D.等边三角形每个内角都等于60°
B
3.如图所示,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
四、当堂练习
4.等腰三角形的一个角是50°,则它一腰上的高与底边的夹角是( )
A.25° B.40°
C.25°或40° D.不能确定
C
D
6.如图所示,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD= ∠CAE,若BD=7,则CE的长为 .
5.如图所示,小艾同学坐在秋千上,秋千旋转了80°,小艾同学的位置也从A点运动到了A'点,则∠OAA'的度数为 .
四、当堂练习
50°
7
7.若等腰三角形一腰上的高与另一腰的夹角的度数为20°,则该等腰三角形顶角的度数为 .
110°或70°
四、当堂练习
8.如图所示,在△ABC中,AB=AC,D是BC边的中点,∠B=30°.求∠ADC和∠BAD的度数.
解:因为AB=AC,D是BC边的中点,
所以AD⊥BC,即∠ADC=∠ADB= 90°.
又因为∠B=30°,
所以∠BAD=60°.
四、当堂练习
9.如图所示,在△ABC中,AB=AC,∠A=40°,BD平分∠ABC,求∠BDC的度数.
解:因为AB=AC,∠A=40°,
所以∠ABC=∠C==70°.
因为BD平分∠ABC,
所以∠BDC=180°-∠DBC-∠C=75°.
所以∠DBC=∠ABC=35°.
10.如图所示,在△ABC中,AB=AC,D是BC边的中点,连接AD, BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)试说明:∠FBE=∠FEB.
四、当堂练习
解:(1)因为AB=AC,所以∠C=∠ABC.
因为∠C=36°,所以∠ABC=36°.
因为BD=CD,AB=AC,
所以AD⊥BC,所以∠ADB=90°,
所以∠BAD=90°-36°=54°.
(2)因为BE平分∠ABC,
所以∠ABE=∠CBE.
因为EF∥BC,所以∠FEB=∠CBE,所以∠FBE=∠FEB.
五、课堂小结
简单的轴对称图形-等腰三角形
等腰三角形的两个底角相等.
等腰三角形的顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
等腰三角形是轴对称图形.
等腰三角形的性质
等边三角形的性质
(1)等边三角形是轴对称图形,有3条对称轴.
(2)等边三角形每条边都相等,每个角都相等,都等于60°.
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合(“三线合一”).
六、作业布置
习题5.3
第1课时
北师大版 数学 七年级下册
3 简单的轴对称图形
第五章 生活中的轴对称
学习目标
1.理解并掌握等腰三角形的性质;(重点)
2.探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.(难点)
一、导入新课
复习回顾
1.轴对称的性质:
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴
,对应线段 ,对应角 .
垂直平分
相等
相等
2.画轴对称图形:
(1)找:找 ;
(2)作:作关键点的 ;
(3)连:按已知图形的方式连接各关键点的对应点.
关键点
对应点
观察下列图片,它们有什么共同的特征?
一、导入新课
情境导入
等腰三角形是生活中常见的图形,它有什么特征 下面我们一起来探究!
二、新知探究
探究一:等腰三角形的性质
如图,在△ABC中,AB=AC,则三角形为等腰三角形.
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫腰;
腰
腰
底边
(2)另一边叫底边;
顶角
底角
底角
(3)两腰的夹角∠A叫顶角;
(4)腰与底边夹角∠B、∠C叫底角.
议一议:(1)等腰三角形是轴对称图形吗 如果是,请找出它的对称轴.
二、新知探究
解:(1)等腰三角形是轴对称图形.
(2)等腰三角形顶角平分线所在的直线是它的对称轴吗
(2)等腰三角形顶角平分线所在的直线是它的对称轴.
如图,将等腰三角形沿过顶点的直线折叠,使得两底角重合,折痕所在的直线即为等腰三角形的对称轴.
二、新知探究
(3)等腰三角形底边上的中线所在的直线是它的对称轴吗 底边上的高所在的直线呢
(4)沿对称轴对折,你能发现等腰三角形的哪些特征 说说你的理由.
(3)都是它的对称轴.
(4)答案不唯一,如等腰三角形的两个底角相等.
二、新知探究
知识归纳
(1)等腰三角形是 图形.
(2)等腰三角形顶角的 、底边上的 、底边上的 重合(也称“三线合一”),它们所在的直线都是等腰三角形的 .
(3)等腰三角形的两个底角 .
轴对称
平分线
中线
高
对称轴
相等
等腰三角形的性质
A
B
C
二、新知探究
跟踪练习
1.等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.
A
分类讨论思想.
2.如图所示,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.试说明:∠CBE=∠BAD.
二、新知探究
跟踪练习
解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,AD⊥BC.
又∵BE⊥AC,
∴∠CBE+∠C=∠CAD+∠C=90°,
∴∠CBE=∠CAD,
∴∠CBE=∠BAD.
二、新知探究
(1)等腰三角形“三线合一”的性质是说明角相等、线段相等和垂直关系的既重要又简便的方法;
(2)在等腰三角形中,作“三线”中的“一线”,利用“三线合一”的性质是解决有关等腰三角形问题的常见方法.
方法归纳
想一想: (1)等边三角形有几条对称轴
二、新知探究
探究二:等边三角形的性质
(2)你能发现它的哪些特征
解:(1)等边三角形有3条对称轴.
(2)等边三角形是轴对称图形,三个内角都为60°,三条边都相等.
等边三角形是特殊的等腰三角形,具有等腰三角形的所有的性质.
二、新知探究
(1)等边三角形是轴对称图形,有 条对称轴.
(2)等边三角形每条边都 ,每个角都 ,都等于 .
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合(“三线合一”).
三
相等
相等
60°
知识归纳
等边三角形的性质
A
B
C
3.如图所示,△ABC是等边三角形,D是BC的中点,点E在AC上,且AE=AD,求∠EDC的度数.
二、新知探究
解: 因为△ABC是等边三角形,D是BC的中点,
所以AD⊥BC,∠DAC=30°,
所以∠ADC=90°.
因为AE=AD,
所以∠ADE==75°,
所以∠EDC=∠ADC-∠ADE=90°-75°=15°.
跟踪练习
二、新知探究
议一议:你有哪些办法可以得到一个等腰三角形?与同伴进行交流.
方法:折一折,剪一剪.
把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC是等腰三角形.
A
B
C
展开
例1:如图所示,在△ABC中,AB=AC,AD是BC边上的高,过点C作CE∥AB交AD的延长线于点E.试说明:CE=AB.
三、典例精析
解:因为AB=AC,AD是BC边上的高,
所以BD=CD.
因为CE∥AB,
所以∠E=∠BAE.
在△ABD和△ECD中,
因为∠ADB=∠EDC,∠BAD=∠E,BD=CD,
所以△ABD≌△ECD(AAS).所以CE=AB.
例2:如图所示,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.试说明:∠DBC=∠E.
三、典例精析
解:因为△ABC是等边三角形,
所以∠ABC=∠ACB=60°,AB=BC,
所以∠ACE=120°.
因为D为AC的中点,AB=BC,
因为CE=CD,
所以∠DBC=∠E.
2.如图所示,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30°
C.45° D.60°
四、当堂练习
A
1.下列说法中错误的是( )
A.等腰三角形的两个底角相等
B.等边三角形有一条对称轴
C.等腰三角形底边上的中线平分顶角
D.等边三角形每个内角都等于60°
B
3.如图所示,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC
C.AD平分∠BAC D.AB=2BD
四、当堂练习
4.等腰三角形的一个角是50°,则它一腰上的高与底边的夹角是( )
A.25° B.40°
C.25°或40° D.不能确定
C
D
6.如图所示,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD= ∠CAE,若BD=7,则CE的长为 .
5.如图所示,小艾同学坐在秋千上,秋千旋转了80°,小艾同学的位置也从A点运动到了A'点,则∠OAA'的度数为 .
四、当堂练习
50°
7
7.若等腰三角形一腰上的高与另一腰的夹角的度数为20°,则该等腰三角形顶角的度数为 .
110°或70°
四、当堂练习
8.如图所示,在△ABC中,AB=AC,D是BC边的中点,∠B=30°.求∠ADC和∠BAD的度数.
解:因为AB=AC,D是BC边的中点,
所以AD⊥BC,即∠ADC=∠ADB= 90°.
又因为∠B=30°,
所以∠BAD=60°.
四、当堂练习
9.如图所示,在△ABC中,AB=AC,∠A=40°,BD平分∠ABC,求∠BDC的度数.
解:因为AB=AC,∠A=40°,
所以∠ABC=∠C==70°.
因为BD平分∠ABC,
所以∠BDC=180°-∠DBC-∠C=75°.
所以∠DBC=∠ABC=35°.
10.如图所示,在△ABC中,AB=AC,D是BC边的中点,连接AD, BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)试说明:∠FBE=∠FEB.
四、当堂练习
解:(1)因为AB=AC,所以∠C=∠ABC.
因为∠C=36°,所以∠ABC=36°.
因为BD=CD,AB=AC,
所以AD⊥BC,所以∠ADB=90°,
所以∠BAD=90°-36°=54°.
(2)因为BE平分∠ABC,
所以∠ABE=∠CBE.
因为EF∥BC,所以∠FEB=∠CBE,所以∠FBE=∠FEB.
五、课堂小结
简单的轴对称图形-等腰三角形
等腰三角形的两个底角相等.
等腰三角形的顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
等腰三角形是轴对称图形.
等腰三角形的性质
等边三角形的性质
(1)等边三角形是轴对称图形,有3条对称轴.
(2)等边三角形每条边都相等,每个角都相等,都等于60°.
(3)等边三角形每条边上的中线、高、该边所对角的平分线重合(“三线合一”).
六、作业布置
习题5.3
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
