10.5 分式方程(第3课时)课件(共29张PPT)-八年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 10.5 分式方程(第3课时)课件(共29张PPT)-八年级数学下册同步精品课堂(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 19:10:10 | ||
图片预览








文档简介
(共29张PPT)
第10章 · 分式
10.5 分式方程(3)
第3课时 分式方程的应用
学习目标
1.能列出分式方程解决简单的实际问题;
2.能根据具体问题的实际意义检验方程解是否合理.
知识回顾
分式方程
整式方程
转化
去分母
一化二解三验四结论
有两种方法:
第一种是代入最简公分母;
第二种代入原分式方程.通常使用第一种方法.
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
知识回顾
4. 列方程(组)解应用题的一般步骤是什么?
1审
“审”是指读懂题目—
2设
3列
“设”是指未知数—
“验”就是验解—
6答
“答”就是写出答案,注意答案完整.
4解
5验
“解”就是解方程—
“列”就是列方程—
审清题意,明确题目中的己知量、未知量,以及题中的等量关系;
设出恰当的未知数,包括直接设和间接设以及设辅助末知数,注意单位;
列代数式表示等量关系中的各个量,就得到含有未知数的等式,即方程;
求出未知数的值;
检验所得的解是不是所列方程的解并符合实际问题的要求;
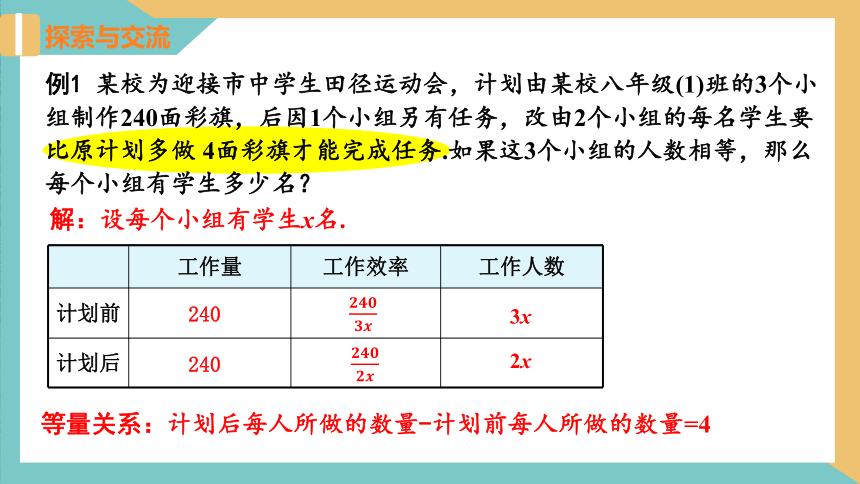
例1 某校为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因1个小组另有任务,改由2个小组的每名学生要比原计划多做 4面彩旗才能完成任务.如果这3个小组的人数相等,那么每个小组有学生多少名?
探索与交流
工作量 工作效率 工作人数
计划前
计划后
240
240
解:设每个小组有学生x名.
3x
2x
等量关系:计划后每人所做的数量-计划前每人所做的数量=4
探索与交流
例1 某校为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因1个小组另有任务,改由2个小组的每名学生要比原计划多做 4面彩旗才能完成任务.如果这3个小组的人数相等,那么每个小组有学生多少名?
解:设每个小组有学生x名.
= 4 .
根据题意,得
解这个方程,得
x = 10.
经检验,x = 10是所列方程的解.
答:每个小组有学生10名.
还有其它解法吗?
探索与交流
例1 某校为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因1个小组另有任务,改由2个小组的每名学生要比原计划多做 4面彩旗才能完成任务.如果这3个小组的人数相等,那么每个小组有学生多少名?
解法2:设2个小组每名学生原计划做y面彩旗,实际做(y+4)面.
= .
根据题意,得
解这个方程,得
y = 8.
经检验,y = 8是所列方程的解.
答:每个小组有学生10名.
=10.
例2 甲、乙两公司各为“见义勇为基金会”捐款30 000元,已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元,甲、乙两公司各有多少人?
探索与交流
捐款总额 人均捐款额 人数
甲
乙
30000
30000
解:设乙公司有x人,则甲公司有(1+20%)x人.
x
(1+20%)x
等量关系:乙公司人均捐款额-甲公司人均捐款额=20
例2 甲、乙两公司各为“见义勇为基金会”捐款30 000元,已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元,甲、乙两公司各有多少人?
探索与交流
= 20 .
根据题意,得
解这个方程,得
x = 250.
经检验,x = 250是所列方程的解.
答:甲公司有300人,乙公司有250人.
(1+20%)x=300.
解:设乙公司有x人,则甲公司有(1+20%)x人.
还有其它解法吗?
例3 小明用12元买软面笔记本,小丽用21元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗
探索与交流
总价 单价 数量
软面笔记本
硬面笔记本
12
21
解:设软面笔记本每本x元,则硬面笔记本每本(x+1.2)元.
x
x+1.2
等量关系:软面笔记本的数量=硬面笔记本的数量
例3 小明用12元买软面笔记本,小丽用21元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗
探索与交流
解:设软面笔记本每本x元,则硬面笔记本每本(x+1.2)元.
= .
根据题意,得
解这个方程,得
x = 1.6.
经检验,x =1.6是所列方程的解.
答:小明和小丽不能买到相同数量的笔记本.
但按此价格,他们都买了7.5本笔记本,不是整数,不符合实际意义.
还有其它解法吗?
归纳总结
列分式方程解决实际问题的一般步骤:
审清题意
设未知数
找等量关系
列出分式方程
解分式方程
验根
是否是原分式方程的根
是否符合题意
写出答案
参见解分式方程的一般步骤
注意:检验是分式方程不可缺少的步骤,既要检验是否是所列方程的解,又要检验是否符合问题的实际意义.
新知巩固
1.一个分数的分母比它的分子大5,如果将这个分数的分子加上14,分母减去1,那么所得分数是原来的倒数.求原分数.
解:设分子为x,则分母为x+5.
= .
根据题意,得
解这个方程,得
x = 4.
经检验,x = 4是所列方程的解.
答:原分数为 .
原分数为.
新知巩固
2.甲、乙两个机器人检测零件,甲比乙每小时多检测10个,甲检测300个与乙检测200个所用的时间相等.甲、乙两个机器人每小时各检测零件多少个?
解:设甲机器人每小时检测零件x个,则乙机器人每小时检测零件(x-10)个.
= .
根据题意,得
解这个方程,得
x = 30.
经检验,x = 30是所列方程的解.
答:甲、乙机器人每小时各检测零件为30个、20个.
x-10=20个.
思维提升
0
180
200
问题1 五一假期,朋友们一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少?
思维提升
问题1 五一假期,朋友们一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少?
解:设小轿车的速度为xkm/h,则面包车速度为(x+10)km/h.
= .
根据题意,得
解这个方程,得
x = 90.
经检验,x = 90是所列方程的解且符合题意.
答:面包车的速度为100km/h,小轿车的速度为90km/h.
x+10=100km/h.
思维提升
问题2 小轿车发现跟丢了,为了追上面包车,他马上提速,在他们约定的300公里处碰头,两车正好同时到达,请问小轿车提速多少?
0
180
200
300
思维提升
问题2 小轿车发现跟丢了,为了追上面包车,他马上提速,在他们约定的300公里处碰头,两车正好同时到达,请问小轿车提速多少?
解:设小轿车提速xkm/h.
= .
根据题意,得
解这个方程,得
x = 30.
经检验,x = 30是所列方程的解且符合题意.
答:小轿车提速30km/h.
归纳总结
实际应用题中常见的数量关系:
(1)利润问题:利润=售价-进价;利润率=×100%;
(2)工程问题:工作量=工作效率×工作时间;
(3)行程问题:路程=速度×时间.
课堂小结
10.4 分式方程(3)
列分式方程解决实际问题的一般步骤
常见类型:行程问题、工程问题、数字问题、顺逆问题、利润问题等
审设列解验答
注意两次验根.
当堂检测
1. 周末,几名同学准备租一辆面包车前往“马陵山”游玩,面包车的租价为180元.出发时,又增加了2名同学,结果每名同学比原来少分担3元车费.设原来参加游玩的同学为x人,则可得方程( )
A. -=3 B. -=3
C. -=3 D. -=3
A
当堂检测
2. 赵强同学借了一本书,共280页,要在两周内读完. 当他读了一半时,发现平均每天要多读21页才能在规定时间内读完. 他读前一半时,平均每天读多少页?如果设他读前一半时,平均每天读x页,则下面所列方程中,正确的是 ( )
A. +=14 B. +=14
C. +=14 D. ++=1
C
当堂检测
3.某市为解决部分市民冬季集中取暖问题,需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程-=15,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天完成
B.每天比原计划少铺设10米,结果延期15天完成
C.每天比原计划多铺设10米,结果提前15天完成
D.每天比原计划少铺设10米,结果提前15天完成
C
当堂检测
4. 甲、乙两车分别从A地出发到B地,A、B两地的路程为40千米,甲车比乙车早出发10分钟,两车同时到达B地.若乙车每小时比甲车多行
驶12千米.设乙车的速度为x千米/时,依题意列方程______________.
- =
5. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,现在平均每天生产________台机器.
200
当堂检测
7. A地在河的上游,B地在河的下游,若船从A地开往B地的速度为v1,从B地返回A地的速度为v2,则船在A、B两地间往返一次的平均速度为_______.
6.某工厂一台机器的工作效率相当于一个工人工作效率的12倍,用这台机器生产60个零件比8个工人生产这些零件少用2小时,则这台机器每小时生产______个零件.
15
当堂检测
8. 端午节前后,张阿姨两次到超市购买同一种粽子.节前,按标价购买,用了96元;节后,按标价的6折购买,用了72元,两次一共购买了27个.这种粽子的标价是多少元每个?
解:设这种粽子的标价是x元/个,则节后的价格是0.6x元/个.
根据题意,得+=27,解得x=8.
经检验,x=8是所列方程的解,且符合题意.
答:这种粽子的标价是8元/个.
当堂检测
9.(2022·烟台)扫地机器人具备敏捷的转弯、制动能力和强大的自主感知、规划能力,深受人们喜爱.某商场根据市场需求,采购了A,B两种型号扫地机器人.已知B型每个进价比A型的2倍少400元.采购相同数量的A,B两种型号扫地机器人,分别用了96000元和168000元.请问A,B两种型号扫地机器人每个进价分别为多少元?
解:设每个A型扫地机器人的进价为x元,则每个B型扫地机器人的进价为(2x-400)元,
根据题意,得=,
解得x=1600,
经检验,x=1600是所列方程的解,且符合题意,
∴2x-400=2×1600-400=2800.
答:每个A型扫地机器人的进价为1600元,每个B型扫地机器人的进价为2800元.
当堂检测
10.(2023·宁夏)“人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.
(1)求两种型号玩具的单价各是多少元?
根据题意,甲、乙两名同学分别列出如下方程:
甲:,解得,经检验是原方程的解.
乙:,解得,经检验是原方程的解.
则甲所列方程中的表示____________________,
乙所列方程中的表示______________________;
型玩具的单价
购买型玩具的数量
当堂检测
(2)该经营者准备用1350元以原单价再次购进这两种型号的玩具共200个,则最多可购进型玩具多少个?
(2)设购进型玩具个,则购买型玩具个,
由(1)中甲同学所列方程的解可知:型玩具的单价为5元,则型玩具的单价为元,
由题意,得:,
解得:,
∵为整数,
∴;
答:最多购进型玩具个.
第10章 · 分式
10.5 分式方程(3)
第3课时 分式方程的应用
学习目标
1.能列出分式方程解决简单的实际问题;
2.能根据具体问题的实际意义检验方程解是否合理.
知识回顾
分式方程
整式方程
转化
去分母
一化二解三验四结论
有两种方法:
第一种是代入最简公分母;
第二种代入原分式方程.通常使用第一种方法.
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
知识回顾
4. 列方程(组)解应用题的一般步骤是什么?
1审
“审”是指读懂题目—
2设
3列
“设”是指未知数—
“验”就是验解—
6答
“答”就是写出答案,注意答案完整.
4解
5验
“解”就是解方程—
“列”就是列方程—
审清题意,明确题目中的己知量、未知量,以及题中的等量关系;
设出恰当的未知数,包括直接设和间接设以及设辅助末知数,注意单位;
列代数式表示等量关系中的各个量,就得到含有未知数的等式,即方程;
求出未知数的值;
检验所得的解是不是所列方程的解并符合实际问题的要求;
例1 某校为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因1个小组另有任务,改由2个小组的每名学生要比原计划多做 4面彩旗才能完成任务.如果这3个小组的人数相等,那么每个小组有学生多少名?
探索与交流
工作量 工作效率 工作人数
计划前
计划后
240
240
解:设每个小组有学生x名.
3x
2x
等量关系:计划后每人所做的数量-计划前每人所做的数量=4
探索与交流
例1 某校为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因1个小组另有任务,改由2个小组的每名学生要比原计划多做 4面彩旗才能完成任务.如果这3个小组的人数相等,那么每个小组有学生多少名?
解:设每个小组有学生x名.
= 4 .
根据题意,得
解这个方程,得
x = 10.
经检验,x = 10是所列方程的解.
答:每个小组有学生10名.
还有其它解法吗?
探索与交流
例1 某校为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因1个小组另有任务,改由2个小组的每名学生要比原计划多做 4面彩旗才能完成任务.如果这3个小组的人数相等,那么每个小组有学生多少名?
解法2:设2个小组每名学生原计划做y面彩旗,实际做(y+4)面.
= .
根据题意,得
解这个方程,得
y = 8.
经检验,y = 8是所列方程的解.
答:每个小组有学生10名.
=10.
例2 甲、乙两公司各为“见义勇为基金会”捐款30 000元,已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元,甲、乙两公司各有多少人?
探索与交流
捐款总额 人均捐款额 人数
甲
乙
30000
30000
解:设乙公司有x人,则甲公司有(1+20%)x人.
x
(1+20%)x
等量关系:乙公司人均捐款额-甲公司人均捐款额=20
例2 甲、乙两公司各为“见义勇为基金会”捐款30 000元,已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元,甲、乙两公司各有多少人?
探索与交流
= 20 .
根据题意,得
解这个方程,得
x = 250.
经检验,x = 250是所列方程的解.
答:甲公司有300人,乙公司有250人.
(1+20%)x=300.
解:设乙公司有x人,则甲公司有(1+20%)x人.
还有其它解法吗?
例3 小明用12元买软面笔记本,小丽用21元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗
探索与交流
总价 单价 数量
软面笔记本
硬面笔记本
12
21
解:设软面笔记本每本x元,则硬面笔记本每本(x+1.2)元.
x
x+1.2
等量关系:软面笔记本的数量=硬面笔记本的数量
例3 小明用12元买软面笔记本,小丽用21元买硬面笔记本.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗
探索与交流
解:设软面笔记本每本x元,则硬面笔记本每本(x+1.2)元.
= .
根据题意,得
解这个方程,得
x = 1.6.
经检验,x =1.6是所列方程的解.
答:小明和小丽不能买到相同数量的笔记本.
但按此价格,他们都买了7.5本笔记本,不是整数,不符合实际意义.
还有其它解法吗?
归纳总结
列分式方程解决实际问题的一般步骤:
审清题意
设未知数
找等量关系
列出分式方程
解分式方程
验根
是否是原分式方程的根
是否符合题意
写出答案
参见解分式方程的一般步骤
注意:检验是分式方程不可缺少的步骤,既要检验是否是所列方程的解,又要检验是否符合问题的实际意义.
新知巩固
1.一个分数的分母比它的分子大5,如果将这个分数的分子加上14,分母减去1,那么所得分数是原来的倒数.求原分数.
解:设分子为x,则分母为x+5.
= .
根据题意,得
解这个方程,得
x = 4.
经检验,x = 4是所列方程的解.
答:原分数为 .
原分数为.
新知巩固
2.甲、乙两个机器人检测零件,甲比乙每小时多检测10个,甲检测300个与乙检测200个所用的时间相等.甲、乙两个机器人每小时各检测零件多少个?
解:设甲机器人每小时检测零件x个,则乙机器人每小时检测零件(x-10)个.
= .
根据题意,得
解这个方程,得
x = 30.
经检验,x = 30是所列方程的解.
答:甲、乙机器人每小时各检测零件为30个、20个.
x-10=20个.
思维提升
0
180
200
问题1 五一假期,朋友们一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少?
思维提升
问题1 五一假期,朋友们一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少?
解:设小轿车的速度为xkm/h,则面包车速度为(x+10)km/h.
= .
根据题意,得
解这个方程,得
x = 90.
经检验,x = 90是所列方程的解且符合题意.
答:面包车的速度为100km/h,小轿车的速度为90km/h.
x+10=100km/h.
思维提升
问题2 小轿车发现跟丢了,为了追上面包车,他马上提速,在他们约定的300公里处碰头,两车正好同时到达,请问小轿车提速多少?
0
180
200
300
思维提升
问题2 小轿车发现跟丢了,为了追上面包车,他马上提速,在他们约定的300公里处碰头,两车正好同时到达,请问小轿车提速多少?
解:设小轿车提速xkm/h.
= .
根据题意,得
解这个方程,得
x = 30.
经检验,x = 30是所列方程的解且符合题意.
答:小轿车提速30km/h.
归纳总结
实际应用题中常见的数量关系:
(1)利润问题:利润=售价-进价;利润率=×100%;
(2)工程问题:工作量=工作效率×工作时间;
(3)行程问题:路程=速度×时间.
课堂小结
10.4 分式方程(3)
列分式方程解决实际问题的一般步骤
常见类型:行程问题、工程问题、数字问题、顺逆问题、利润问题等
审设列解验答
注意两次验根.
当堂检测
1. 周末,几名同学准备租一辆面包车前往“马陵山”游玩,面包车的租价为180元.出发时,又增加了2名同学,结果每名同学比原来少分担3元车费.设原来参加游玩的同学为x人,则可得方程( )
A. -=3 B. -=3
C. -=3 D. -=3
A
当堂检测
2. 赵强同学借了一本书,共280页,要在两周内读完. 当他读了一半时,发现平均每天要多读21页才能在规定时间内读完. 他读前一半时,平均每天读多少页?如果设他读前一半时,平均每天读x页,则下面所列方程中,正确的是 ( )
A. +=14 B. +=14
C. +=14 D. ++=1
C
当堂检测
3.某市为解决部分市民冬季集中取暖问题,需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程-=15,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天完成
B.每天比原计划少铺设10米,结果延期15天完成
C.每天比原计划多铺设10米,结果提前15天完成
D.每天比原计划少铺设10米,结果提前15天完成
C
当堂检测
4. 甲、乙两车分别从A地出发到B地,A、B两地的路程为40千米,甲车比乙车早出发10分钟,两车同时到达B地.若乙车每小时比甲车多行
驶12千米.设乙车的速度为x千米/时,依题意列方程______________.
- =
5. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,现在平均每天生产________台机器.
200
当堂检测
7. A地在河的上游,B地在河的下游,若船从A地开往B地的速度为v1,从B地返回A地的速度为v2,则船在A、B两地间往返一次的平均速度为_______.
6.某工厂一台机器的工作效率相当于一个工人工作效率的12倍,用这台机器生产60个零件比8个工人生产这些零件少用2小时,则这台机器每小时生产______个零件.
15
当堂检测
8. 端午节前后,张阿姨两次到超市购买同一种粽子.节前,按标价购买,用了96元;节后,按标价的6折购买,用了72元,两次一共购买了27个.这种粽子的标价是多少元每个?
解:设这种粽子的标价是x元/个,则节后的价格是0.6x元/个.
根据题意,得+=27,解得x=8.
经检验,x=8是所列方程的解,且符合题意.
答:这种粽子的标价是8元/个.
当堂检测
9.(2022·烟台)扫地机器人具备敏捷的转弯、制动能力和强大的自主感知、规划能力,深受人们喜爱.某商场根据市场需求,采购了A,B两种型号扫地机器人.已知B型每个进价比A型的2倍少400元.采购相同数量的A,B两种型号扫地机器人,分别用了96000元和168000元.请问A,B两种型号扫地机器人每个进价分别为多少元?
解:设每个A型扫地机器人的进价为x元,则每个B型扫地机器人的进价为(2x-400)元,
根据题意,得=,
解得x=1600,
经检验,x=1600是所列方程的解,且符合题意,
∴2x-400=2×1600-400=2800.
答:每个A型扫地机器人的进价为1600元,每个B型扫地机器人的进价为2800元.
当堂检测
10.(2023·宁夏)“人间烟火味,最抚凡人心”,地摊经济、小店经济是就业岗位的重要来源.某经营者购进了型和型两种玩具,已知用520元购进型玩具的数量比用175元购进型玩具的数量多30个,且型玩具单价是型玩具单价的倍.
(1)求两种型号玩具的单价各是多少元?
根据题意,甲、乙两名同学分别列出如下方程:
甲:,解得,经检验是原方程的解.
乙:,解得,经检验是原方程的解.
则甲所列方程中的表示____________________,
乙所列方程中的表示______________________;
型玩具的单价
购买型玩具的数量
当堂检测
(2)该经营者准备用1350元以原单价再次购进这两种型号的玩具共200个,则最多可购进型玩具多少个?
(2)设购进型玩具个,则购买型玩具个,
由(1)中甲同学所列方程的解可知:型玩具的单价为5元,则型玩具的单价为元,
由题意,得:,
解得:,
∵为整数,
∴;
答:最多购进型玩具个.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
