20.1 平均数 课件(共36张PPT)-八年级数学下册同步精品课堂(华东师大版)
文档属性
| 名称 | 20.1 平均数 课件(共36张PPT)-八年级数学下册同步精品课堂(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 19:05:00 | ||
图片预览










文档简介
20.1 平均数
数学(华东师大版)
八年级 下册
第二十章 数据的整理与初步处理
学习目标
1.掌握平均数的概念,会求一组数据的平均数;
2.会用平均数解决实际生活中的问题;
3.掌握加权平均数的概念,会求一组数据的加权平均数;
4.会用加权平均数解决实际生活中的问题.
导入新课
7
6
5
4
3
2
1
A B C D
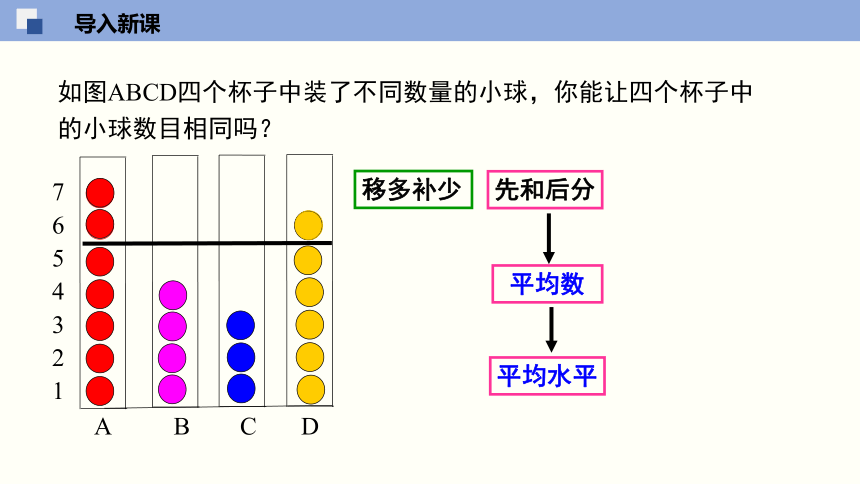
平均数
先和后分
移多补少
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
平均水平
讲授新课
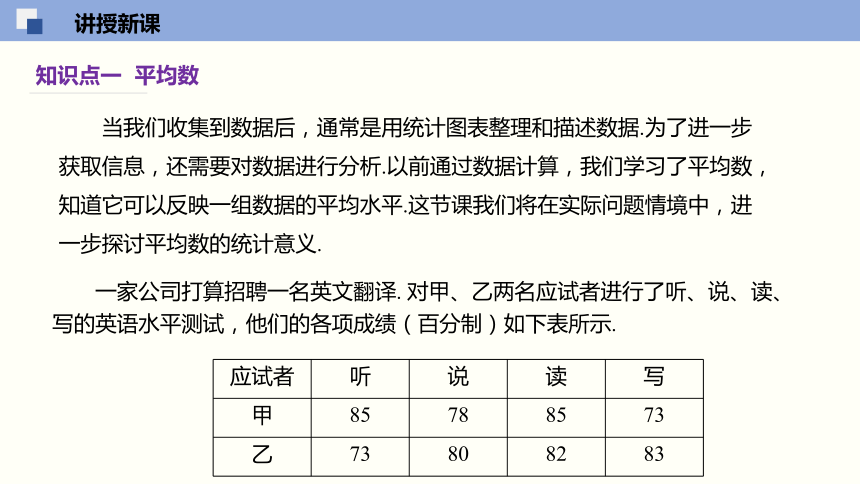
知识点一 平均数
当我们收集到数据后,通常是用统计图表整理和描述数据.为了进一步获取信息,还需要对数据进行分析.以前通过数据计算,我们学习了平均数,知道它可以反映一组数据的平均水平.这节课我们将在实际问题情境中,进一步探讨平均数的统计意义.
一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示.
{5940675A-B579-460E-94D1-54222C63F5DA}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
讲授新课
解:根据平均数公式,甲的平均成绩为
乙的平均成绩为
因为甲的平均成绩比乙高,所以应该录取甲.
问题1:如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
讲授新课
归纳总结
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,如果有 n 个数据 x1,x2,…,xn,我们把 表示这组数据的平均数,用“ ” 表示 ,即
讲授新课
特别提醒:
一组数据的平均数是唯一的,它不一定是数据中的某个数据;
平均数的大小与一组数据里的每个数据都有关,其中任何一个数据的变动都会引起平均数的变动.
讲授新课
典例精析
【例1】植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
(2)总共植树多少棵?
(3)平均每人植树多少棵?
讲授新课
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人)
(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
(3)平均每人植树 (棵)
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
讲授新课
练一练
1、某班级为了解同学年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
解:这个班级学生的平均年龄为:
所以,这个班级学生的平均年龄约为14岁.
讲授新课
2、已知2、3、4、x1、x2、x3的平均数是5,则x1、x2、x3的平均数是________。
【分析】∵2、3、4、x1、x2、x3的平均数是5,
∴2+3+4+x1+x2+x3=30,
∴x1+x2+x3=21,
则x1、x2、x3的平均数是21÷3=7。
7
讲授新课
知识点二 加权平均数
情境引入
超市中有各种各样的苹果,每种苹果的价格都不样,如果小明的妈妈买了3.5元/千克的苹果1千克,买了6元/千克的苹果3千克,那么小明妈妈所买苹果的平均价格是两个单价相加除以2吗?为什么?
讲授新课
为了解某市九年级学生开展“综合与实践”活动的情况,抽样调查了该市200名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制条形统计图如下:
求这200名学生参加“综合与实践”活动的平均天数。
讲授新课
以下是某位同学的解题过程,请判断是否正确~
????+????+????+????+????????=4(天)
?
不正确,这200名学生参加“综合与实践”活动的平均天数,不仅与参加活动的天数有关,还与相应的人数有关。
讲授新课
【正解】????×????????+????×????????+????×????????+????×????????+????×????????????????????=4.5(天)
?
讲授新课
某电视台要招聘1名记者,甲、乙、丙三人应聘参加了3项素质测试,成绩如下(单位:分):
如果采访写作、计算机操作和创意设计的成绩按5:2:3计算,那么哪个人的素质测试平均成绩最高?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
讲授新课
采访写作、计算机操作和创意设计成绩按5:2:3计算,说明采访写作、计算机操作、创意设计的“重要程度”不一样,它们分别占总成绩的????????+????+????、????????+????+????、????????+????+????。
?
甲的得分=70×????????+????+????+60×????????+????+????+86×????????+????+????
=72.8(分);
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
讲授新课
乙的得分=90×????????+????+????+75×????????+????+????+51×????????+????+????
=75.3(分);
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
乙的平均成绩最高
丙的得分=60×????????+??+????+84×????????+????+????+78×????????+????+????
=70.2(分)。
?
讲授新课
如果采访写作、计算机操作和创意设计成绩按4:2:4计算,那么哪个人的素质测试平均成绩最高?
甲的得分=70×????????+????+????+60×????????+????+????+86×????????+????+????=74.4(分);
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
乙的得分=90×????????+????+????+75×????????+????+????+51×????????+????+????=71.4(分);
?
丙的得分=60×????????+????+????+84×????????+????+????+78×????????+????+????=72(分)。
?
甲的平均成绩最高
讲授新课
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫做这n个数的加权平均数.
归纳
概念归纳
讲授新课
典例精析
【例2】一次演讲比赛中,评委将从演讲内容,演讲能力,演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
讲授新课
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
权
50%
40%
10%
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
讲授新课
你能说说平均数与加权平均数的区别和联系吗?
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用平均数.
1.平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);
议一议
讲授新课
知识点三 加权平均数的实际应用
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个数的算术平均数
也叫做x1,x2,…,xk这n个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
知识要点
讲授新课
【例3】某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
=
≈______(岁).
答:这个跳水队运动员的平均年龄约为_____.
8
16
24
2
14
14岁
讲授新课
练一练
1、某校八年级一班有学生50人,八年级二班有学生45人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:(81.5×50 +83.4×45)÷95
=7828÷95
=82.4
答:这两个班95名学生的平均分是82.4分.
当堂检测
1.已知7,4,5和x的平均数是6,则x= .
2.某组学生进行“引体向上”测试,有2名学生做了8次,其余4名学生分别做了10次、7次、6次、9次,那么这组学生的平均成绩是 次,在平均成绩之上的有 人.
8
8
2
3.如果一组数据中有3个6、4个-1、2个-2、1个0和3个x,其中平均数为x,那么x= .
1
当堂检测
解: 甲的平均成绩为 ,
4.如果公司想招一名综合能力较强的翻译,请计算两名应聘者的平均成绩,应该录用谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
当堂检测
5.已知:x1,x2,x3,…,?x10的平均数是a,x11,x12,x13,…?,x30
的平均数是b,则x1,x2,x3,…?,x30的平均数是(??? ?)
A.(a+b)??? B.(a+b)?? C.(a+3b)/3?? ?? D.(a+2b)/3
D
6.若x1,x2,…,?xn的平均数为a,
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,…?,10xn?的平均数为 .
a+3
10a
当堂检测
7.已知一组数据4,13,24的权数分别是
则这组数据的加权平均数是________ .
解析:
17
当堂检测
8.某次歌唱比赛,两名选手的成绩如下:
(1)若按三项平均值取第一名,则______是第一名.
测试选手
测试成绩
创新
唱功
综合知识
A
72
85
67
B
85
74
70
选手B
当堂检测
(2)解:
所以,此时第一名是选手A
(2)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁?
当堂检测
9.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
当堂检测
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
课堂小结
平均数
概念
计算
公式
计算器求平均值
加权平均数
谢 谢~
数学(华东师大版)
八年级 下册
第二十章 数据的整理与初步处理
学习目标
1.掌握平均数的概念,会求一组数据的平均数;
2.会用平均数解决实际生活中的问题;
3.掌握加权平均数的概念,会求一组数据的加权平均数;
4.会用加权平均数解决实际生活中的问题.
导入新课
7
6
5
4
3
2
1
A B C D
平均数
先和后分
移多补少
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
平均水平
讲授新课
知识点一 平均数
当我们收集到数据后,通常是用统计图表整理和描述数据.为了进一步获取信息,还需要对数据进行分析.以前通过数据计算,我们学习了平均数,知道它可以反映一组数据的平均水平.这节课我们将在实际问题情境中,进一步探讨平均数的统计意义.
一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示.
{5940675A-B579-460E-94D1-54222C63F5DA}应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
讲授新课
解:根据平均数公式,甲的平均成绩为
乙的平均成绩为
因为甲的平均成绩比乙高,所以应该录取甲.
问题1:如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
讲授新课
归纳总结
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,如果有 n 个数据 x1,x2,…,xn,我们把 表示这组数据的平均数,用“ ” 表示 ,即
讲授新课
特别提醒:
一组数据的平均数是唯一的,它不一定是数据中的某个数据;
平均数的大小与一组数据里的每个数据都有关,其中任何一个数据的变动都会引起平均数的变动.
讲授新课
典例精析
【例1】植树节到了, 某单位组织职工开展植树竞赛, 下图反映的是植树量与人数之间的关系.
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
请根据图中信息计算:
(1)总共有多少人参加了本次活动?
(2)总共植树多少棵?
(3)平均每人植树多少棵?
讲授新课
解:(1)参加本次活动的总人数是1+8+1+10+8+3+1=32(人)
(2)总共植树3×8+4×1+5×10+6×8+7×3+8×1=155(棵).
(3)平均每人植树 (棵)
3
4
5
6
7
8
棵数
12
10
8
6
4
2
0
人数
0
讲授新课
练一练
1、某班级为了解同学年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个班级学生的平均年龄(结果取整数).
解:这个班级学生的平均年龄为:
所以,这个班级学生的平均年龄约为14岁.
讲授新课
2、已知2、3、4、x1、x2、x3的平均数是5,则x1、x2、x3的平均数是________。
【分析】∵2、3、4、x1、x2、x3的平均数是5,
∴2+3+4+x1+x2+x3=30,
∴x1+x2+x3=21,
则x1、x2、x3的平均数是21÷3=7。
7
讲授新课
知识点二 加权平均数
情境引入
超市中有各种各样的苹果,每种苹果的价格都不样,如果小明的妈妈买了3.5元/千克的苹果1千克,买了6元/千克的苹果3千克,那么小明妈妈所买苹果的平均价格是两个单价相加除以2吗?为什么?
讲授新课
为了解某市九年级学生开展“综合与实践”活动的情况,抽样调查了该市200名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制条形统计图如下:
求这200名学生参加“综合与实践”活动的平均天数。
讲授新课
以下是某位同学的解题过程,请判断是否正确~
????+????+????+????+????????=4(天)
?
不正确,这200名学生参加“综合与实践”活动的平均天数,不仅与参加活动的天数有关,还与相应的人数有关。
讲授新课
【正解】????×????????+????×????????+????×????????+????×????????+????×????????????????????=4.5(天)
?
讲授新课
某电视台要招聘1名记者,甲、乙、丙三人应聘参加了3项素质测试,成绩如下(单位:分):
如果采访写作、计算机操作和创意设计的成绩按5:2:3计算,那么哪个人的素质测试平均成绩最高?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
讲授新课
采访写作、计算机操作和创意设计成绩按5:2:3计算,说明采访写作、计算机操作、创意设计的“重要程度”不一样,它们分别占总成绩的????????+????+????、????????+????+????、????????+????+????。
?
甲的得分=70×????????+????+????+60×????????+????+????+86×????????+????+????
=72.8(分);
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
讲授新课
乙的得分=90×????????+????+????+75×????????+????+????+51×????????+????+????
=75.3(分);
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
乙的平均成绩最高
丙的得分=60×????????+??+????+84×????????+????+????+78×????????+????+????
=70.2(分)。
?
讲授新课
如果采访写作、计算机操作和创意设计成绩按4:2:4计算,那么哪个人的素质测试平均成绩最高?
甲的得分=70×????????+????+????+60×????????+????+????+86×????????+????+????=74.4(分);
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
采访写作
计算机操作
创意设计
甲
70
60
86
乙
90
75
51
丙
60
84
78
乙的得分=90×????????+????+????+75×????????+????+????+51×????????+????+????=71.4(分);
?
丙的得分=60×????????+????+????+84×????????+????+????+78×????????+????+????=72(分)。
?
甲的平均成绩最高
讲授新课
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫做这n个数的加权平均数.
归纳
概念归纳
讲授新课
典例精析
【例2】一次演讲比赛中,评委将从演讲内容,演讲能力,演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
讲授新课
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
权
50%
40%
10%
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
讲授新课
你能说说平均数与加权平均数的区别和联系吗?
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用平均数.
1.平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);
议一议
讲授新课
知识点三 加权平均数的实际应用
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个数的算术平均数
也叫做x1,x2,…,xk这n个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
知识要点
讲授新课
【例3】某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
=
≈______(岁).
答:这个跳水队运动员的平均年龄约为_____.
8
16
24
2
14
14岁
讲授新课
练一练
1、某校八年级一班有学生50人,八年级二班有学生45人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:(81.5×50 +83.4×45)÷95
=7828÷95
=82.4
答:这两个班95名学生的平均分是82.4分.
当堂检测
1.已知7,4,5和x的平均数是6,则x= .
2.某组学生进行“引体向上”测试,有2名学生做了8次,其余4名学生分别做了10次、7次、6次、9次,那么这组学生的平均成绩是 次,在平均成绩之上的有 人.
8
8
2
3.如果一组数据中有3个6、4个-1、2个-2、1个0和3个x,其中平均数为x,那么x= .
1
当堂检测
解: 甲的平均成绩为 ,
4.如果公司想招一名综合能力较强的翻译,请计算两名应聘者的平均成绩,应该录用谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
当堂检测
5.已知:x1,x2,x3,…,?x10的平均数是a,x11,x12,x13,…?,x30
的平均数是b,则x1,x2,x3,…?,x30的平均数是(??? ?)
A.(a+b)??? B.(a+b)?? C.(a+3b)/3?? ?? D.(a+2b)/3
D
6.若x1,x2,…,?xn的平均数为a,
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,…?,10xn?的平均数为 .
a+3
10a
当堂检测
7.已知一组数据4,13,24的权数分别是
则这组数据的加权平均数是________ .
解析:
17
当堂检测
8.某次歌唱比赛,两名选手的成绩如下:
(1)若按三项平均值取第一名,则______是第一名.
测试选手
测试成绩
创新
唱功
综合知识
A
72
85
67
B
85
74
70
选手B
当堂检测
(2)解:
所以,此时第一名是选手A
(2)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁?
当堂检测
9.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
当堂检测
解:选手A的最后得分是
85×50%+95×40%+95×10%
50%+40%+10%
=42.5+38+9.5
=90.
选手B的最后得分是
95×50%+85×40%+95×10%
50%+40%+10%
=47.5+34+9.5
=91.
由上可知选手B获得第一名,选手A获得第二名.
选手
演讲内容
(50%)
演讲能力
(40%)
演讲效果
(10%)
A
85
95
95
B
95
85
95
课堂小结
平均数
概念
计算
公式
计算器求平均值
加权平均数
谢 谢~
