第四章 三角形(单元复习课件 共14张PPT)-七年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 第四章 三角形(单元复习课件 共14张PPT)-七年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 426.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 19:23:47 | ||
图片预览






文档简介
(共14张PPT)
第四章 三角形
章末复习
七
下
数
学
2020
回顾 & 思考
一、三角形的有关性质
1.不在同一直线上的三条线段首尾_________所组成的图形叫作三角形. 以点A,B,C为定点的三角形记为______,读作“三角形ABC”.
顺次相接
△ABC
2.三角形三个内角的和等于______.
180°
锐角三角形
直角三角形
钝角三角形
按角分
按边分
不等边三角形
等腰三角形
5.三角形的三边关系
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
3. 三角形的分类
4.直角三角形的两个锐角互余.
二、全等三角形
1.全等三角形的性质:
对应角相等,对应边相等
3.三角形的稳定性的依据:
SSS
2.全等三角形的判定
ASA
SSS
SAS
AAS
探索&交流
典例精析
例1.下列各组长度的线段为边,能构成三角形的是( )
A.7cm、5cm、12cm B.6cm、8cm、15cm
C.8cm、4cm、3cm D.4cm、6cm、5cm.
D
探索&交流
典例精析
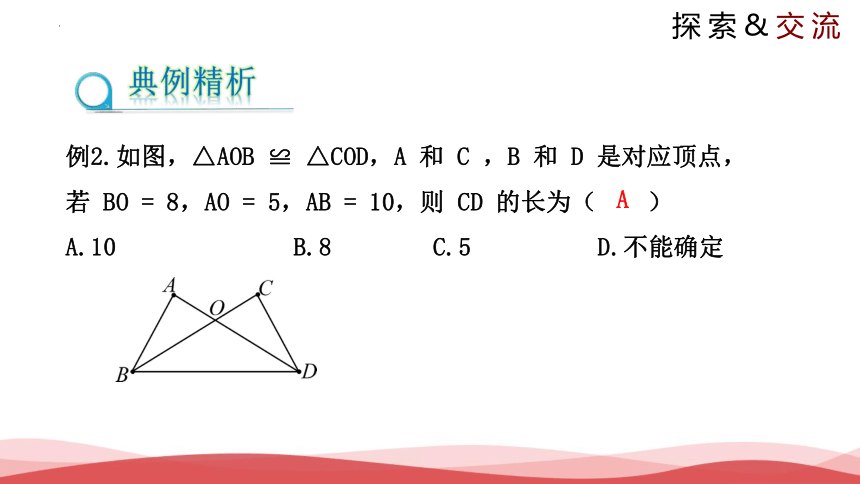
例2.如图,△AOB ≌ △COD,A 和 C ,B 和 D 是对应顶点,若 BO = 8,AO = 5,AB = 10,则 CD 的长为( )
A.10 B.8 C.5 D.不能确定
A
典例精析
例3.如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:因为∠A=50°,∠B=70°,
所以∠ACB=180°-∠A-∠B
=180°-50° -70°=60°.
因为CD是∠ACB的平分线,
所以∠BCD= ∠ACB= ×60°=30°.
因为DE∥BC,
所以∠EDC=∠BCD=30°,
∠BDC=180°-∠B-∠BCD=80°.
探索&交流
典例精析
例4.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,
试说明:∠DEC=∠FEC.
A
B
C
D
F
E
G
A
B
C
D
F
E
G
解: 因为CE⊥AD, 所以 ∠AGE=∠AGC=90 °.
在△AGE和△AGC中,
∠AGE=∠AGC,
AG=AG,
∠EAG=∠CAG,
所以 △AGE ≌ △AGC(ASA),
所以 GE =GC.
在△DGE和△DGC中,
EG=CG,
∠ EGD=∠CGD=90 °,
DG=DG.
所以△DGE ≌△DGC(SAS).
所以∠DEG=∠DCG.
因为EF//BC,
所以∠FEC=∠ECD,
所以∠DEG =∠FEC.
探索&交流
典例精析
例5.如图,△ABC中,BD平分∠ABC, ∠1=∠2, ∠3= ∠C,求∠1的度数.
A
B
C
D
)
)
)
)
2
4
1
3
解:设∠1=x,根据题意可得∠2=x.
因为∠3=∠1+∠2,∠4=∠2,
所以∠3=2x, ∠4=x,
又因为∠3=∠C,所以∠C=2x.
在△ABC中,x+2x+2x=180 °,
解得x=36°, 所以∠1=36 °.
随堂练习
练习&巩固
1.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
A. ∠ADB =∠ADC B.∠B =∠C
C. DB = DC D.AB = AC
C
2.如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=132°,那么∠A的度数是 .
A
B
C
D
E
O
84°
练习&巩固
3.如图AB=CD,BC=AD,则∠B与∠D相等吗?试说明你的理由.
解:∠B = ∠D.
理由:如图,连接 AC ,
因AB = CD,AC = CA,BC = DA,
所以△ABC ≌ △CDA ,
所以∠B = ∠D.
A
C
B
D
练习&巩固
4.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=____.
解析:因为点D是AC的中点,所以AD= AC,
因为S△ABC=12,
所以S△ABD= S△ABC= ×12=6.
因为EC=2BE,S△ABC=12,
所以S△ABE= S△ABC= ×12=4.
因为S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF-S△BEF,
所以S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
2
第四章 三角形
章末复习
七
下
数
学
2020
回顾 & 思考
一、三角形的有关性质
1.不在同一直线上的三条线段首尾_________所组成的图形叫作三角形. 以点A,B,C为定点的三角形记为______,读作“三角形ABC”.
顺次相接
△ABC
2.三角形三个内角的和等于______.
180°
锐角三角形
直角三角形
钝角三角形
按角分
按边分
不等边三角形
等腰三角形
5.三角形的三边关系
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
3. 三角形的分类
4.直角三角形的两个锐角互余.
二、全等三角形
1.全等三角形的性质:
对应角相等,对应边相等
3.三角形的稳定性的依据:
SSS
2.全等三角形的判定
ASA
SSS
SAS
AAS
探索&交流
典例精析
例1.下列各组长度的线段为边,能构成三角形的是( )
A.7cm、5cm、12cm B.6cm、8cm、15cm
C.8cm、4cm、3cm D.4cm、6cm、5cm.
D
探索&交流
典例精析
例2.如图,△AOB ≌ △COD,A 和 C ,B 和 D 是对应顶点,若 BO = 8,AO = 5,AB = 10,则 CD 的长为( )
A.10 B.8 C.5 D.不能确定
A
典例精析
例3.如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:因为∠A=50°,∠B=70°,
所以∠ACB=180°-∠A-∠B
=180°-50° -70°=60°.
因为CD是∠ACB的平分线,
所以∠BCD= ∠ACB= ×60°=30°.
因为DE∥BC,
所以∠EDC=∠BCD=30°,
∠BDC=180°-∠B-∠BCD=80°.
探索&交流
典例精析
例4.如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交AB于点E,EF∥BC交AC于点F,
试说明:∠DEC=∠FEC.
A
B
C
D
F
E
G
A
B
C
D
F
E
G
解: 因为CE⊥AD, 所以 ∠AGE=∠AGC=90 °.
在△AGE和△AGC中,
∠AGE=∠AGC,
AG=AG,
∠EAG=∠CAG,
所以 △AGE ≌ △AGC(ASA),
所以 GE =GC.
在△DGE和△DGC中,
EG=CG,
∠ EGD=∠CGD=90 °,
DG=DG.
所以△DGE ≌△DGC(SAS).
所以∠DEG=∠DCG.
因为EF//BC,
所以∠FEC=∠ECD,
所以∠DEG =∠FEC.
探索&交流
典例精析
例5.如图,△ABC中,BD平分∠ABC, ∠1=∠2, ∠3= ∠C,求∠1的度数.
A
B
C
D
)
)
)
)
2
4
1
3
解:设∠1=x,根据题意可得∠2=x.
因为∠3=∠1+∠2,∠4=∠2,
所以∠3=2x, ∠4=x,
又因为∠3=∠C,所以∠C=2x.
在△ABC中,x+2x+2x=180 °,
解得x=36°, 所以∠1=36 °.
随堂练习
练习&巩固
1.如图,已知∠1=∠2,要说明△ABD≌△ACD,还需从下列条件中选一个,错误的选法是( )
A. ∠ADB =∠ADC B.∠B =∠C
C. DB = DC D.AB = AC
C
2.如图,在△ABC中,两条角平分线BD和CE相交于点O,若∠BOC=132°,那么∠A的度数是 .
A
B
C
D
E
O
84°
练习&巩固
3.如图AB=CD,BC=AD,则∠B与∠D相等吗?试说明你的理由.
解:∠B = ∠D.
理由:如图,连接 AC ,
因AB = CD,AC = CA,BC = DA,
所以△ABC ≌ △CDA ,
所以∠B = ∠D.
A
C
B
D
练习&巩固
4.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=____.
解析:因为点D是AC的中点,所以AD= AC,
因为S△ABC=12,
所以S△ABD= S△ABC= ×12=6.
因为EC=2BE,S△ABC=12,
所以S△ABE= S△ABC= ×12=4.
因为S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF-S△BEF,
所以S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
