专题01 平面图形的认识(二)(复习课件 共56张PPT)-七年级数学下学期期末考点大串讲(苏科版)
文档属性
| 名称 | 专题01 平面图形的认识(二)(复习课件 共56张PPT)-七年级数学下学期期末考点大串讲(苏科版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览










文档简介
七年级苏科版数学下册期中考点大串讲
串讲01 平面图形的认识(二)
01
02
目
录
考点剖析
考点透视
四大常考点思维导图梳理
四大考点知识梳理+易错易混/技巧+热考题型
考点透视
考点剖析
考点一 平行线的性质与判定
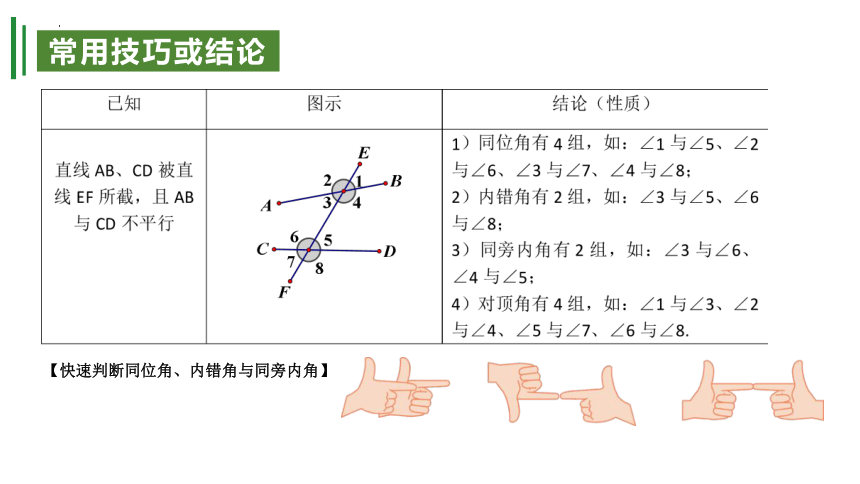
三线八角的概念:指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对. 正确认识这八个角要抓住:同位角位置相同即“同旁和同侧”;内错角要抓住“内部和异侧”;同旁内角要抓住“同旁和内部”.
平行线的定义:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示.
平行公理(唯一性):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论(传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合.
平行线之间的距离概念:两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离.
性质:1)夹在两条平行线间的平行线段处处相等;
2)平行线间的距离处处相等.
考点剖析
考点一 平行线的性质与判定
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补..
平行线的判定
判定方法1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行.
判定方法2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行.
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行.
判定方法4:垂直于同一直线的两直线互相平行.
易错易混
考点一 平行线的性质与判定
1. 平行线必在同一平面内,分别在两个平面内的两条直线,即使不相交,也可以不平行,因此“在同一平面内”是平行线存在的前提条件.
2. 平行线指的是“两条直线”而不是两条射线或线段,今后遇到线段、射线平行时,特指线段、射线所在的直线平行.
3. 在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论. 这是平行线特有的性质不要一提同位角或内错角就认为它们相等,一提同旁内角就认为互补,若没有两直线平行的条件,这些是不成立的.
常用技巧或结论
【快速判断同位角、内错角与同旁内角】
常用技巧或结论
热考题型
考点一 平行线的性质与判定
热考题型
考点一 平行线的性质与判定
3(23-24七年级上·安徽宿州·期中)在同一平面内两条直线的位置关系可能是(????)
A.相交或垂直 B.垂直或平行 C.平行或相交 D.相交或重合
4(22-23七年级下·天津和平·期末)下列说法中正确的是(????)
A.过一点有且只有一条直线垂直于已知直线
B.直线外一点到这条直线的垂线段,叫做这点到这条直线距离
C.经过直线外一点,有且仅有一条直线与已知直线平行
D.两条直线被第三条直线所截,同旁内角互补
5(21-22七年级下·山东菏泽·期中)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(????)
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
热考题型
考点一 平行线的性质与判定
热考题型
考点一 平行线的性质与判定
7.(23-24七年级下·福建厦门·期中)如图,∠????=90°,????????⊥????????于点A,????????平分∠????????????.
(1)证明????????∥????????;
(2)探究∠????????????与∠????????????的数量关系,并说明理由.
?
【详解】(1)解:∠????????????=∠????????????,
∵????????⊥????????,
∴∠????????????=90°=∠????
∴????????∥????????;
(2)∵????????∥????????,
∴∠????????????=∠????????????,
∵????????平分∠????????????,
∴∠????????????=∠????????????,
∴∠????????????=∠????????????.
?
热考题型
考点一 平行线的性质与判定
8.(22-23七年级下·河北廊坊·期中)如图,在△????????????中,∠????=20°,点D是????????上一点,点E是三角形外一点,且∠????????????=20°,点F为线段????????上一点,连接????????,且????????∥????????.
(1)请判断????????与????????的位置关系,并证明;
(2)若∠????=75°,求∠????????????的度数;
(3)若∠????=2∠????????????,2∠????????????=3∠????????????,求∠????的度数.
?
【详解】(1)解:????????∥????????,
证明如下:∵∠????????????=20°,∠????=20°,∴∠????=∠????????????=20°,
∴????????∥????????;
(2)解:∵????????∥????????,∴∠????+∠????????????=180°,
∵∠????=75°∴∠????????????=180°?75°=105°.
?
热考题型
考点一 平行线的性质与判定
8.(22-23七年级下·河北廊坊·期中)如图,在△????????????中,∠????=20°,点D是????????上一点,点E是三角形外一点,且∠????????????=20°,点F为线段????????上一点,连接????????,且????????∥????????.
(1)请判断????????与????????的位置关系,并证明;
(2)若∠????=75°,求∠????????????的度数;
(3)若∠????=2∠????????????,2∠????????????=3∠????????????,求∠????的度数.
?
(3)解:设∠????????????=????,则∠????=2????,2∠????????????=3????,
∵????????∥????????,∴∠????+∠????????????=180°,
∴2????+32????+????=180°,解得????=40°,
∴∠????????????=40°×32=60°,∴∠????????????=60°+40°=100°,
∵????????∥????????,∴∠????+∠????????????=180°,
∴∠????=80°.
?
热考题型
考点一 平行线的性质与判定
9. 为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图是某同学“抖空竹”时的一个瞬间,王聪把它抽象成如图的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°,求∠E的度数.
【详解】如图所示:延长DC交AE于点F,
∵AB∥CD,∠EAB=80°,
∴∠EAB=∠EFC=80°,
∵∠ECD=∠E+∠EFC,
∴∠E=∠ECD﹣∠EFC,
∵∠ECD=110°
∴∠E=110°﹣80°=30°.
热考题型
考点一 平行线的性质与判定
11(21-22七年级下·湖南张家界·期末)如图:CD∥AB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是(????)
A.①②③ B.①②④ C.②③④ D.①②③④
?
12(21-22七年级下·湖北武汉·期中)如图,某人骑自行车自????沿正东方向前进,第一次在????处拐弯,两次拐弯后,仍沿正东方向行驶,两次拐弯的角度可能是( )
A.第一次右拐15°,第二次左拐165°
B.第一次右拐15°,第二次左拐15°
C.第一次左拐15°,第二次左拐165°
D.第一次右拐165°,第二次左拐165°
?
热考题型
考点一 平行线的性质与判定
13.(23-24七年级下·江苏苏州·期中)如图,在△????????????中,????????=6cm.射线????????∥????????,点????从点????出发沿射线????????以2cm/s的速度运动,当点????出发1s后,点????也从点????出发沿射线????????以3cm/s的速度运动,分别连接????????,????????.设点????运动时间为????s,其中????>0.
(1)若∠????????????<∠????????????,则????的取值范围是 ;
(2)当????为何值时,????????=????????;
(3)是否存在某一时刻????,使????△????????????+????△????????????=????△????????????.若存在,请求出????的值;若不存在请说明理由.
?
【详解】(1)解:∵∠????????????<∠????????????,∴????????∴ 3?????1<6 解得:????<3,
∴当0故答案为:0?
热考题型
考点一 平行线的性质与判定
13.(23-24七年级下·江苏苏州·期中)如图,在△????????????中,????????=6cm.射线????????∥????????,点????从点????出发沿射线????????以2cm/s的速度运动,当点????出发1s后,点????也从点????出发沿射线????????以3cm/s的速度运动,分别连接????????,????????.设点????运动时间为????s,其中????>0.
(1)若∠????????????<∠????????????,则????的取值范围是 ;
(2)当????为何值时,????????=????????;
(3)是否存在某一时刻????,使????△????????????+????△????????????=????△????????????.若存在,请求出????的值;若不存在请说明理由.
?
(2)由题意得:????????=2????,????????= 3?????1,
∴????????=6? 3?????1或??????= 3?????1?6,
∵????????=????????,∴2????=6? 3?????1或2????=3?????1?6,
解得:????=95或9,
即????=95或9时,????????=????????;
?
热考题型
考点一 平行线的性质与判定
13.(23-24七年级下·江苏苏州·期中)如图,在△????????????中,????????=6cm.射线????????∥????????,点????从点????出发沿射线????????以2cm/s的速度运动,当点????出发1s后,点????也从点????出发沿射线????????以3cm/s的速度运动,分别连接????????,????????.设点????运动时间为????s,其中????>0.
(1)若∠????????????<∠????????????,则????的取值范围是 ;
(2)当????为何值时,????????=????????;
(3)是否存在某一时刻????,使????△????????????+????△????????????=????△????????????.若存在,请求出????的值;若不存在请说明理由.
?
(3)∵ ????△????????????+????△????????????=????△????????????,????△????????????+????△????????????=????△????????????,
∴ ????△????????????=????△???????????? (点????在线段????????上),
∵???????? ∥ ????????,∴△????????????和△????????????的高相等,
∴????????=????????,即2????=6? 3?????1,解得:????=95,
即当????=95秒时,????△????????????+????△????????????=????△????????????.
?
考点剖析
考点二 三角形的概念及性质
三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所构成的图形叫做三角形.
三角形的表示:用符号“Δ”表示,顶点是A、B、C的三角形记作“ΔABC”,读作“三角形ABC”.
三角形的分类:
1)三角形按边分类:三角形三边都不相等的三角形???????????????????????????????????????等腰三角形等边三角形???????????????????????????????????底边和腰不相等的等腰三角形
2)三角形按角分类:三角形直角三角形??????????????????斜三角形锐角三角形钝角三角形
?
三角形的稳定性: 三角形三条边的长度确定之后,三角形的形状就唯一确定了.
?
考点剖析
考点二 三角形的概念及性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}重要线段
概念
图形
性质
三角形的高
从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高).
∵AD是?ABC中BC边的高
∴∠ADB=∠ADC=90°
三角形的中线
在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线
∵AD是?ABC中BC边的中线
∴BD=CD S△ABD=S△ADC
三角形的角平分线
三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线.
∵AD是?ABC中∠BAC的角平分线
∴∠BAD=∠DAC=∠BAC
考点剖析
考点二 三角形的概念及性质
三角形三边关系定理:三角形的两边之和大于第三边.
推论:三角形的两边之差小于第三边.
三角形的内角和定理:三角形三个内角和等于180°.
推论:直角三角形的两个锐角互余.
三角形的内角和定理的应用:
1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数;
2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数;
3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数.
三角形的外角和定理:三角形的外角和等于360°.
三角形的外角和的性质:1)三角形的一个外角等于和它不相邻的两个内角的和;
2)三角形的一个外角大于任何一个和它不相邻的内角.
常用技巧或结论
三角形的稳定性解题技巧:
1)当三角形三条边的长度确定之后,三角形的形状就唯一确定了.
2)四边形及多边形不具有稳定性,要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了.
三角形三边关系定理及推论的应用:
1)判断三条已知线段能否组成三角形,只需检验最短的两边之和大于第三边,则可说明能组成三角形.
2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b
3)所有通过周长相加减求三角形的边,求出两个答案的,要注意检查每个答案能否组成三角形.
热考题型
考点二 三角形的概念及性质
1.(23-24七年级上·山东烟台·期中)如图所示的五边形边框,木匠师傅至少需要再钉 根木条才能使其不变形.
2.(22-23七年级下·山东枣庄·期末)如图,????????,????????,????????分别是△????????????的中线、角平分线、高线,下列结论中错误的是(????)
A.????????=12???????? B.2∠????????????=∠????????????
C.∠????+∠????????????=90° D.????????=????????
?
热考题型
考点二 三角形的概念及性质
3.(23-24七年级下·湖北咸宁·期中)如图,直线????∥????,????????与????,????分别相交于点????,????,且????????⊥????????,????????交直线????于点????.
(1)若∠1=60°,求∠2的度数;
(2)若????????=5,????????=12,????????=13,求点????到直线????的距离.
?
【详解】(1)解:∵直线????∥????,
∴∠3=∠1=60°,
又∵????????⊥????????,
∴∠2=90°?∠3=30°;
(2)如图,过????作????????⊥????????于????,则????????的长即为直线????与????的距离.
∵????△????????????=12×????????×????????=12×????????×????????,
∴????????=????????×????????????????=12×513=6013,
∴点????到直线????的距离为6013.
?
热考题型
考点二 三角形的概念及性质
4.(23-24七年级下·福建泉州·期中)如图,在△????????????中,????????是中线,????????=10cm,????????=6cm.
(1)△????????????与△????????????的周长差为_______cm.
(2)点E在边????????上,连接????????,若三角形????????????的周长被????????分成的两部分的差是2cm,求线段????????的长.
?
【详解】(1)解:△????????????的周长=????????+????????+????????,△????????????的周长=????????+????????+????????,
∵????????是中线,∴????????=????????,
△????????????与△????????????的周长差:????????+????????+?????????????????+????????+????????=?????????????????=4cm
?
(2)解:由图可知:△????????????的周长=????????+????????+????????,四边形????????????????的周长=????????+????????+????????+????????,
①当△????????????的周长-四边形????????????????的周长=2cm时,
∵????是????????的中点,∴????????=????????,
∴????????+????????+?????????????????+????????+????????+????????=2,
∴????????=????????+????????+2,
又∵????????=10cm,????????=6cm,????????=?????????????????,
∴????????+????????+2=?????????????????,
∴10?????????=????????+6+2???∴????????=1cm;
?
热考题型
考点二 三角形的概念及性质
4.(23-24七年级下·福建泉州·期中)如图,在△????????????中,????????是中线,????????=10cm,????????=6cm.
(1)△????????????与△????????????的周长差为_______cm.
(2)点E在边????????上,连接????????,若三角形????????????的周长被????????分成的两部分的差是2cm,求线段????????的长.
?
②四边形????????????????的周长-当△????????????的周长=2cm时,
∵????是????????的中点,
∴????????=????????,
∴????????+????????+????????+?????????????????+????????+????????=2,
∴????????+????????=????????+2,
又∵????????=10cm,????????=6cm,????????=?????????????????,
∴????????+????????=?????????????????+2,
∴????????+6=10?????????+2
∴????????=3cm;
综上,线段????????的长为1cm或3cm.
?
热考题型
考点二 三角形的概念及性质
5.(23-24七年级下·广东深圳·期中)已知△????????????的三边长为a,b,c,且a,b,c都是整数.
(1)若????=2,????=5,且c为偶数.求△????????????的周长.
(2)化简:?????????+???????????????????+????+????+????.
?
【详解】(1)解:∵????=2,?????=5,
∴5?2由于c是偶数,则????=4或6,
当????=4时,△????????????的周长为????+????+????=2+5+4=11,
当????=6时,△????????????的周长为????+????+????=2+5+6=13.
综上所述,△????????????的周长为11或13.
(2)解:∵△????????????的三边长为a,b,c,∴????+????>????,
∴|?????????+????|?|??????????????|+|????+????+????|
=????+??????????(????+?????????)+????+????+????
=????+????+????.
?
热考题型
考点二 三角形的概念及性质
6.(23-24七年级下·全国·课后作业)在△????????????中,????????=2cm,????????=9cm.
(1)求第三边????????长的取值范围;
(2)若第三边????????的长是偶数,求????????的长;
(3)若△????????????是等腰三角形,求其周长.
?
【详解】(1)解:∵在△????????????中,????????=2cm,????????=9cm,
∴?????????????????∴9?2cm(2)解:∵7cm∴第三边????????的长为8cm或10cm;
(3)解;∵7cm∴只能是????????=????????=9cm,
∴△????????????的周长为9+9+2=20cm.
?
热考题型
考点二 三角形的概念及性质
热考题型
考点二 三角形的概念及性质
8.(23-24八年级上·湖北武汉·阶段练习)已知:等腰三角形的三边长分别为3?????2,2?????1,????+3,求这个三角形的底边长.
?
【详解】解:①当3?????2是底边时,2?????1=????+3,解得:????=4,
∴2?????1=????+3=4+3=7,3?????2=3×4?2=10,
此时三边为:7,7,10,7?7<10<7+7,满足三边关系,故底边为:10,
②当????+3是底边时,2?????1=3?????2,解得:????=1,
∴2?????1=3?????2=3×1?2=1,????+3=1+3=4,
此时三边为:1,1,4,1?1<4>1+1,不满足三边关系,此类情况不存在,
③当2?????1是底边时,????+3=3?????2,解得:????=52,
∴????+3=3?????2=3×52?2=112,2?????1=2×52?1=4,
此时三边为:112,112,4,112?112<4<112+112,
满足三边关系,故底边为:4,
综上所述:底边为4或10.
?
热考题型
考点二 三角形的概念及性质
9.(22-23七年级下·黑龙江哈尔滨·期中)如图是10×8的网格,网格中每个小正方形的边长均为1,△????????????的三个顶点A、B、C都在小正方形的顶点上,请在图中分别按要求画图:
(1)在图中画△????????????的中线????????;
(2)在图中画△????????????的高线????????.
(3)直接写出△????????????的面积是________.
?
(3)解:????△????????????=12×8×2=8,
?
热考题型
考点二 三角形的概念及性质
10.(22-23七年级上·山东威海·期末)如图,将△????????????沿着????????对折,点A落到????′处,若∠????????????′+∠????????????′=82°,则∠????= ??度.
?
【详解】解:∵将△????????????沿着????????对折,A落到????′,
∴∠????????????=∠????′????????,∠????????????=∠????′????????,
∴∠????????????′+2∠????????????=180°,∠????′????????+2∠????????????=180°,
∴∠????????????′+2∠????????????+∠????′????????+2∠????????????=360°,
∵∠????????????′+∠????????????′=82°,
∴∠????????????+∠????????????=139°,
∴∠????=180°?∠????????????+∠????????????=180°?139°=41°,
?
11.(22-23七年级下·四川成都·期末)若直角三角形的一个锐角等于40°,则它的另一个锐角等于(????)
A.50° B.60° C.70° D.140°
?
热考题型
考点二 三角形的概念及性质
12.(22-23七年级下·广西河池·阶段练习)(1)如图1,已知????????∥????????,点E在两平行线的内侧,连接????????,????????.若∠????????????=35°,∠????????????=25°,求∠????????????的度数;
(2)如图2,已知????????∥????????,点E在两平行线的外侧,连接????????,????????,若∠????????????=????,∠????????????=????.
①求∠????????????的大小(用含α,β的代数式表示);
②作∠????????????的平分线交????????于点G,连接????????,????????平分∠????????????(如图3).若∠????????????=130°,????+????=80°,分别求出α,β的度数.
?
【详解】解:(1)如图1,过点E作????????∥????????.
∵????????∥????????,∴∠????????????=∠????????????=35°.
∵????????∥????????,????????∥????????,
∴????????∥????????.
∴∠????????????=∠????????????=25°.
∴∠????????????=∠????????????+∠????????????=35°+25°=60°.
?
热考题型
考点二 三角形的概念及性质
12.(22-23七年级下·广西河池·阶段练习)(1)如图1,已知????????∥????????,点E在两平行线的内侧,连接????????,????????.若∠????????????=35°,∠????????????=25°,求∠????????????的度数;
(2)如图2,已知????????∥????????,点E在两平行线的外侧,连接????????,????????,若∠????????????=????,∠????????????=????.
①求∠????????????的大小(用含α,β的代数式表示);
②作∠????????????的平分线交????????于点G,连接????????,????????平分∠????????????(如图3).若∠????????????=130°,????+????=80°,分别求出α,β的度数.
?
(2)①∵????????∥????????,
∴∠????????????=∠????????????=????.
又∵∠????????????=∠????????????+∠????????????,∠????????????=????,
∴∠????????????=∠?????????????∠????????????=?????????.
?
热考题型
考点二 三角形的概念及性质
12.(22-23七年级下·广西河池·阶段练习)(1)如图1,已知????????∥????????,点E在两平行线的内侧,连接????????,????????.若∠????????????=35°,∠????????????=25°,求∠????????????的度数;
(2)如图2,已知????????∥????????,点E在两平行线的外侧,连接????????,????????,若∠????????????=????,∠????????????=????.
①求∠????????????的大小(用含α,β的代数式表示);
②作∠????????????的平分线交????????于点G,连接????????,????????平分∠????????????(如图3).若∠????????????=130°,????+????=80°,分别求出α,β的度数.
?
②如图3,
∵????????∥????????,∴∠1=∠2.
又∵????????平分∠????????????,∴∠????????????=∠1=12????.∴∠????????????=∠2.
∵????????平分于∠????????????,∴∠2=∠3.∴∠3=∠????????????=12????.
∵∠????????????=130°,∴∠????????????+∠3=180°?∠????????????=50°.
∴????+12????=50°.又∵????+????=80°,
∴????=20°,????=60°.
?
热考题型
考点二 三角形的概念及性质
13.(23-24七年级下·山东泰安·期中)将一副直角三角板????????????和????????????如图放置(其中∠????=60°,∠????=45°),使点E落在????????边上,且????????∥????????.求∠????????????的度数.
?
【详解】解:∵∠????=∠????=90°,∠????=60°,∠????=45°,
∴ ∠????????????=90°?∠????=30°,∠????????????=90°?∠????=45°,
∵ ????????∥????????,
∴ ∠????????????=∠????????????=30°,
∴ ∠????????????=∠?????????????∠????????????=15°,
∴ ∠????????????=180°?∠????????????=165°.
?
考点剖析
考点三 图形的平移
平移的概念:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.平移不改变图形的形状和大小.
平移的三大要素:1)平移的起点,2)平移的方向,3)平移的距离.
作图步骤:
1)根据题意,确定平移的方向和平移的距离;
2)找出原图形的关键点;
3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;
4)按原图形依次连接对应点,得到平移后的图形.
平移的性质:
1)平移不改变图形的大小、形状,只改变图形的位置,因此平移前后的两个图形全等.
2)平移前后对应线段平行且相等、对应角相等.
3)任意两组对应点的连线平行(或在同一条直线上)且相等,对应点之间的距离就是平移的距离.
热考题型
考点三 图形的平移
1.(21-22七年级下·江苏扬州·阶段练习)下列现象:①荡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动.其中属于平移的是(?????)
A.①② B.①③ C.②③ D.②④
热考题型
考点三 图形的平移
3.(23-24七年级上·山东滨州·期末)如图,在三角形????????????中,????????⊥????????,垂足为????,????????=5,将三角形????????????沿射线????????的方向向右平移后,得到三角形????′????′????′,连接????′????,若????????′=12,????′????=4,则三角形????′????????′的面积为 .
?
【详解】解:由平移可知????????=????′????′,
∵????′????=????????+????′????′?????????′,即4=????????+????′????′?12,
∴????????=????′????′=8,
∴????????′=????′????′?????′????=4,
∴????△????′????????′=12????????′?????????=12×4×5=10.
故答案为:10.
?
热考题型
考点三 图形的平移
4.(23-24七年级上·吉林长春·期末)如图,边长为10cm的正方形????????????????先向上平移5cm,再向右平移2cm,得到正方形????′????′????′????′,此时阴影部分的面积为 cm2.
?
【详解】解:如图,
由平移得:????????=5cm,????′????=2cm,????′????′=????????=10cm,
∴????′????=10?2=8cm,????????=10?5=5cm,
即阴影部分是长为8cm,宽为5cm的长方形,
∴阴影部分的面积为8×5=40 cm2,
故答案为:40.
?
热考题型
考点三 图形的平移
5.(22-23七年级下·贵州遵义·期中)如图,某公园有一块长方形地,准备在长方形地内修筑同样宽的小路(图中阴影部分),余下部分进行绿化,已知小路的宽均为2m,则绿化带的面积是 .
?
【详解】解:由平移的性质可将绿化面积转化为长为40?4=36m,宽为30?2=28m的长方形,
∴除去小路,绿化带的面积为36×28=1008m2,
故答案为:1008m2.
?
热考题型
考点三 图形的平移
6.(22-23七年级下·甘肃陇南·期末)星期天早晨,小刚和爸爸正在商量往楼梯上铺地毯的事,如图所示,
爸爸:“小刚,你帮我算一下,从一层铺到二层需要地毯几米?”
小刚:“我早已用盒尺量好了,每阶高15cm,宽为20cm??…”
爸爸:(打断小刚的话)“不量每阶的高度和宽度,你想想有没有办法?”
小刚:(思索)“有了,只需要量出楼梯的总高和总长度再相加,就行了.”
你认为小刚的方法可以吗?说明理由.
?
【详解】解:可以,
如图所示:根据图示可得:
地毯的总长度=????????+????????=15×9+20×9=15+20×9=315cm=3.15m.
?
考点剖析
考点四 多边形的内角和与外角和
多边形的定义:在平面中,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
多边形的对角线:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.?
多边形内角和定理:n边形的内角和为(n?2)?180°(n≥3).
多边形外角和定理:任意多边形的外角和等于360°,与多边形的形状和边数无关.
正多边形的定义:各角相等,各边相等的多边形叫做正多边形.
解题技巧
考点四 多边形的内角和与外角和
1)正n边形的每个内角为(n?2)×180°????,每一个外角为360°????.
2)正n边形有n条对称轴.
3)对于正n边形,当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形.
4)从n边形的一个顶点可以引(n-3)条对角线,并且这些对角线把多边形分成了(n–2)个三角形,n边形的对角线条数为????(?????3)2?
?
解题技巧
考点四 多边形的内角和与外角和
1)n边形的内角和随边数的增加而增加,边数每增加1,内角和增加180°.
2)任意多边形的内角和均为180°的整数倍.
3)利用多边形内角和定理可解决三类问题:
①已知多边形的边数求内角和;
②已知多边形的内角和求边数;
③已知足够的角度条件下求某一个内角的度数.
热考题型
考点四 多边形的内角和与外角和
1.(23-24七年级上·贵州毕节·期末)若从多边形的一个顶点出发,最多可引3条对角线,则这个多边形的对角线共有(????)
A.6条 B.9条 C.12条 D.18条
2.(23-24九年级上·四川绵阳·期末)从十二边形的一个顶点引对角线,可把这个多边形分成(????)个三角形.
A.10 B.11 C.12 D.13
3.(22-23七年级下·广东惠州·开学考试)一个多边形的内角和是720°,则这个多边形的边数是
?
6
?
4(22-23七年级下·甘肃天水·期末)如图,小明在操场上从????点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地????点时,一共走了(????)米
A.56 B.64 C.80 D.72
?
热考题型
考点四 多边形的内角和与外角和
5.(22-23七年级上·湖北武汉·阶段练习)一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是( )
A.9 B.10 C.8或9或10 D.9或10或11
【详解】解:设内角和为1440°的多边形的边数是n,则(n-2)?180=1440,解得:n=10.
∵截去一个角后边上可以增加1,不变,减少1,∴原多边形的边数是9或10或11.故选:D.
【解题技巧】一个n变形剪去一个角后,若剪去的一个角只经过一个顶点和一边,则剩下的形状是n边形,若剪去的一个角经过两条邻边,则剩下的形状是(n+1)边形,若剪去的一个角经过两个相邻点,则剩下的形状是(n-1)边形.所以遇到相关题目时,要分类讨论.
热考题型
考点四 多边形的内角和与外角和
6.(22-23七年级下·福建泉州·期末)正四边形与其他正多边形组合可以铺设地板,则该多边形可以是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【详解】解:A.正五边形每个内角108°,正四边形每个内角90°,显然不能组合成360°,所以不能铺设地板,不符合题意;
B.正六边形每个内角120°,正四边形每个内角90°,不能组合成360°,所以不能铺设地板,不符合题意;
C.正四边形每个内角90°,正八边形每个内角135°,90°+135°×2=360°,所以能铺设地板,符合题意;
D.因为十边形的每个内角是144°,正四边形的每个内角是90°,不能组合成360°,所以不能铺设地板,不符合题意;故选:C.
?
【解题技巧】解决几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
热考题型
考点四 多边形的内角和与外角和
7.(22-23七年级下·四川眉山·期中)如图,则∠????+∠????+∠????+∠????+∠????+∠????的度数为( )
A.180° B.360° C.540° D.720°
?
【详解】解:如图,连接????????,
由三角形外角的性质可得:∠1=∠????+∠????=∠????????????+∠????????????,
∴∠????????????+∠????+∠????+∠????+∠????+∠????=∠????????????+∠????????????+∠????????????+∠????????????+∠????+∠????
=∠????????????+∠????????????+∠????+∠????
=360°
故选:B.
?
热考题型
考点四 多边形的内角和与外角和
8.(22-23七年级下·河南南阳·期末)已知一个正n边形的内角和是它的外角和的2倍.
(1)求n;
(2)求正n边形每个内角的度数;
(3)用足够多边长相等的这种正n边形和正三角形两种地板镶嵌地面,则一个顶点处需要此正n边形和正三角形的地板块数分别为:__________.
【详解】(1)解:根据题意得:180°?????2=2×360°,
解得????=6.
答:n的值为6.
(2)解:180°?????26=720°6=120°.
答:正n边形每个内角的度数为120°.
?
热考题型
考点四 多边形的内角和与外角和
8.(22-23七年级下·河南南阳·期末)已知一个正n边形的内角和是它的外角和的2倍.
(1)求n;
(2)求正n边形每个内角的度数;
(3)用足够多边长相等的这种正n边形和正三角形两种地板镶嵌地面,则一个顶点处需要此正n边形和正三角形的地板块数分别为:__________.
(3)解:设在平面镶嵌时,围绕在某一点有x个正六边形和y个正三角形的内角可以拼成一个周角,
根据题意可得:120????+60????=360,即:2????+????=6,
∴????=2????=2或????=1????=4
∴一个顶点处需要此正六边形和正三角形的地板块数分别为:2个,2个或1个,4个.
故答案为: 2个,2个或1个,4个.
?
热考题型
考点四 多边形的内角和与外角和
9.(22-23七年级下·江苏苏州·期末)苏州博物馆本馆是国内唯一一座由世界著名建筑大师贝聿铭亲自设计的博物馆,几何形构造的屋顶颇具特色,粉墙黛瓦的传统元素随处可见,现代主义建筑与苏州园林的有机结合,如同姑苏城里一幅旖旎烟雨交织而成的水墨画.图①中的屋顶设计是在传统飞檐翘角基础上演变而来,呈现出强烈的几何感和抽象性,图②中∠1=∠4=116°,∠2=∠3=90°,则下列判断中正确的是(????)
A.∠5=42° B.∠5=52° C.∠5=62° D.∠5的度数无法确定
?
【详解】解:由题意得五边形的内角和为(5?2)×180°=540°,
∵∠1=∠4=116°,∠2=∠3=90°,
∴∠5=180°?(540°?116°?116°?90°?90°)
=180°?128°
=52°,
故选:B.
?
热考题型
考点四 多边形的内角和与外角和
10.(22-23七年级下·湖北孝感·期中)某自然保护区给一些小动物搭建了小木屋,其侧面如图,????????,????????均与地面垂直,小亮看见了也想回家给自己的小狗做一个同样的小木屋,他用量角器测出∠????=123°,∠????=135°.由于小亮个子太矮,屋顶的∠????测不到,哥哥看到后说,不用测量,我也能算出∠????,你知道哥哥是怎样算出∠????的吗?请你帮哥哥算出∠????的度数是 .
?
【详解】根据题意可知∠????????????=∠????????????=90°,多边形????????????????????为五边形,其内角和为180°×5?2=540°,
可得∠????=540°?∠?????∠?????∠?????????????∠????????????=102°.
故答案为:102°.
?
热考题型
考点四 多边形的内角和与外角和
11.(22-23七年级下·江苏扬州·期末)如图,将透明直尺叠放在正五边形徽章????????????????????上,若直尺的下沿????????⊥????????于点O,且经过点B,上沿????????经过点E,则∠????????????的度数为( )
A.152° B.126° C.120° D.108°
?
【详解】解:由题意可得∠????????????=∠????=5?2×180°÷5=108°,
∵????????⊥????????,
∴∠????????????=90°,
∴四边形????????????????中,∠????????????=360°?90°?108°?108°=54°,
∴∠????????????=180°?∠????????????=180°?54°=126°,
故选:B.
?
热考题型
考点四 多边形的内角和与外角和
12.(21-22七年级上·河南信阳·期末)如图,正五边形????????????????????,????????平分∠????????????,????????平分正五边形的外角∠????????????,则∠????=(????)
A.45° B.54° C.60° D.64°
?
【详解】∵正五边形外角和为360°,
∴外角∠????????????=360°5=72°,
∴内角∠????????????=∠????=∠????????????=180°?72°=108°,
∵????????平分∠????????????,????????平分正五边形的外角∠????????????,
∴∠????????????=12∠????????????=54°, ∠????????????=12∠????????????=36°,
在四边形??????????????中,∠????????????+∠????+∠????????????+∠????????????+∠????=360°,
∴∠????=360°?∠????????????+∠????+∠????????????+∠????????????=360°?54°+108°+108°+36°=54°,
故选:B.
串讲01 平面图形的认识(二)
01
02
目
录
考点剖析
考点透视
四大常考点思维导图梳理
四大考点知识梳理+易错易混/技巧+热考题型
考点透视
考点剖析
考点一 平行线的性质与判定
三线八角的概念:指的是两条直线被第三条直线所截而形成的八个角,其中同位角4对,内错角有2对,同旁内角有2对. 正确认识这八个角要抓住:同位角位置相同即“同旁和同侧”;内错角要抓住“内部和异侧”;同旁内角要抓住“同旁和内部”.
平行线的定义:在同一平面内,不相交的两条直线叫做平行线,平行用符号“∥”表示.
平行公理(唯一性):经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论(传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:
①有且只有一个公共点,两直线相交;
②无公共点,则两直线平行;
③两个或两个以上公共点,则两直线重合.
平行线之间的距离概念:两条平行线中,一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离.
性质:1)夹在两条平行线间的平行线段处处相等;
2)平行线间的距离处处相等.
考点剖析
考点一 平行线的性质与判定
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补..
平行线的判定
判定方法1 :两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行.
判定方法2 :两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:内错角相等,两直线平行.
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:同旁内角互补,两直线平行.
判定方法4:垂直于同一直线的两直线互相平行.
易错易混
考点一 平行线的性质与判定
1. 平行线必在同一平面内,分别在两个平面内的两条直线,即使不相交,也可以不平行,因此“在同一平面内”是平行线存在的前提条件.
2. 平行线指的是“两条直线”而不是两条射线或线段,今后遇到线段、射线平行时,特指线段、射线所在的直线平行.
3. 在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论. 这是平行线特有的性质不要一提同位角或内错角就认为它们相等,一提同旁内角就认为互补,若没有两直线平行的条件,这些是不成立的.
常用技巧或结论
【快速判断同位角、内错角与同旁内角】
常用技巧或结论
热考题型
考点一 平行线的性质与判定
热考题型
考点一 平行线的性质与判定
3(23-24七年级上·安徽宿州·期中)在同一平面内两条直线的位置关系可能是(????)
A.相交或垂直 B.垂直或平行 C.平行或相交 D.相交或重合
4(22-23七年级下·天津和平·期末)下列说法中正确的是(????)
A.过一点有且只有一条直线垂直于已知直线
B.直线外一点到这条直线的垂线段,叫做这点到这条直线距离
C.经过直线外一点,有且仅有一条直线与已知直线平行
D.两条直线被第三条直线所截,同旁内角互补
5(21-22七年级下·山东菏泽·期中)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(????)
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
热考题型
考点一 平行线的性质与判定
热考题型
考点一 平行线的性质与判定
7.(23-24七年级下·福建厦门·期中)如图,∠????=90°,????????⊥????????于点A,????????平分∠????????????.
(1)证明????????∥????????;
(2)探究∠????????????与∠????????????的数量关系,并说明理由.
?
【详解】(1)解:∠????????????=∠????????????,
∵????????⊥????????,
∴∠????????????=90°=∠????
∴????????∥????????;
(2)∵????????∥????????,
∴∠????????????=∠????????????,
∵????????平分∠????????????,
∴∠????????????=∠????????????,
∴∠????????????=∠????????????.
?
热考题型
考点一 平行线的性质与判定
8.(22-23七年级下·河北廊坊·期中)如图,在△????????????中,∠????=20°,点D是????????上一点,点E是三角形外一点,且∠????????????=20°,点F为线段????????上一点,连接????????,且????????∥????????.
(1)请判断????????与????????的位置关系,并证明;
(2)若∠????=75°,求∠????????????的度数;
(3)若∠????=2∠????????????,2∠????????????=3∠????????????,求∠????的度数.
?
【详解】(1)解:????????∥????????,
证明如下:∵∠????????????=20°,∠????=20°,∴∠????=∠????????????=20°,
∴????????∥????????;
(2)解:∵????????∥????????,∴∠????+∠????????????=180°,
∵∠????=75°∴∠????????????=180°?75°=105°.
?
热考题型
考点一 平行线的性质与判定
8.(22-23七年级下·河北廊坊·期中)如图,在△????????????中,∠????=20°,点D是????????上一点,点E是三角形外一点,且∠????????????=20°,点F为线段????????上一点,连接????????,且????????∥????????.
(1)请判断????????与????????的位置关系,并证明;
(2)若∠????=75°,求∠????????????的度数;
(3)若∠????=2∠????????????,2∠????????????=3∠????????????,求∠????的度数.
?
(3)解:设∠????????????=????,则∠????=2????,2∠????????????=3????,
∵????????∥????????,∴∠????+∠????????????=180°,
∴2????+32????+????=180°,解得????=40°,
∴∠????????????=40°×32=60°,∴∠????????????=60°+40°=100°,
∵????????∥????????,∴∠????+∠????????????=180°,
∴∠????=80°.
?
热考题型
考点一 平行线的性质与判定
9. 为增强学生体质,感受中国的传统文化,学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图是某同学“抖空竹”时的一个瞬间,王聪把它抽象成如图的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°,求∠E的度数.
【详解】如图所示:延长DC交AE于点F,
∵AB∥CD,∠EAB=80°,
∴∠EAB=∠EFC=80°,
∵∠ECD=∠E+∠EFC,
∴∠E=∠ECD﹣∠EFC,
∵∠ECD=110°
∴∠E=110°﹣80°=30°.
热考题型
考点一 平行线的性质与判定
11(21-22七年级下·湖南张家界·期末)如图:CD∥AB,BC平分∠ACD,CF平分∠ACG,∠BAC=40°,∠1=∠2,则下列结论:①∠ACE=2∠4;②CB⊥CF;③∠1=70°;④∠3=2∠4,其中正确的是(????)
A.①②③ B.①②④ C.②③④ D.①②③④
?
12(21-22七年级下·湖北武汉·期中)如图,某人骑自行车自????沿正东方向前进,第一次在????处拐弯,两次拐弯后,仍沿正东方向行驶,两次拐弯的角度可能是( )
A.第一次右拐15°,第二次左拐165°
B.第一次右拐15°,第二次左拐15°
C.第一次左拐15°,第二次左拐165°
D.第一次右拐165°,第二次左拐165°
?
热考题型
考点一 平行线的性质与判定
13.(23-24七年级下·江苏苏州·期中)如图,在△????????????中,????????=6cm.射线????????∥????????,点????从点????出发沿射线????????以2cm/s的速度运动,当点????出发1s后,点????也从点????出发沿射线????????以3cm/s的速度运动,分别连接????????,????????.设点????运动时间为????s,其中????>0.
(1)若∠????????????<∠????????????,则????的取值范围是 ;
(2)当????为何值时,????????=????????;
(3)是否存在某一时刻????,使????△????????????+????△????????????=????△????????????.若存在,请求出????的值;若不存在请说明理由.
?
【详解】(1)解:∵∠????????????<∠????????????,∴????????∴ 3?????1<6 解得:????<3,
∴当0故答案为:0?
热考题型
考点一 平行线的性质与判定
13.(23-24七年级下·江苏苏州·期中)如图,在△????????????中,????????=6cm.射线????????∥????????,点????从点????出发沿射线????????以2cm/s的速度运动,当点????出发1s后,点????也从点????出发沿射线????????以3cm/s的速度运动,分别连接????????,????????.设点????运动时间为????s,其中????>0.
(1)若∠????????????<∠????????????,则????的取值范围是 ;
(2)当????为何值时,????????=????????;
(3)是否存在某一时刻????,使????△????????????+????△????????????=????△????????????.若存在,请求出????的值;若不存在请说明理由.
?
(2)由题意得:????????=2????,????????= 3?????1,
∴????????=6? 3?????1或??????= 3?????1?6,
∵????????=????????,∴2????=6? 3?????1或2????=3?????1?6,
解得:????=95或9,
即????=95或9时,????????=????????;
?
热考题型
考点一 平行线的性质与判定
13.(23-24七年级下·江苏苏州·期中)如图,在△????????????中,????????=6cm.射线????????∥????????,点????从点????出发沿射线????????以2cm/s的速度运动,当点????出发1s后,点????也从点????出发沿射线????????以3cm/s的速度运动,分别连接????????,????????.设点????运动时间为????s,其中????>0.
(1)若∠????????????<∠????????????,则????的取值范围是 ;
(2)当????为何值时,????????=????????;
(3)是否存在某一时刻????,使????△????????????+????△????????????=????△????????????.若存在,请求出????的值;若不存在请说明理由.
?
(3)∵ ????△????????????+????△????????????=????△????????????,????△????????????+????△????????????=????△????????????,
∴ ????△????????????=????△???????????? (点????在线段????????上),
∵???????? ∥ ????????,∴△????????????和△????????????的高相等,
∴????????=????????,即2????=6? 3?????1,解得:????=95,
即当????=95秒时,????△????????????+????△????????????=????△????????????.
?
考点剖析
考点二 三角形的概念及性质
三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所构成的图形叫做三角形.
三角形的表示:用符号“Δ”表示,顶点是A、B、C的三角形记作“ΔABC”,读作“三角形ABC”.
三角形的分类:
1)三角形按边分类:三角形三边都不相等的三角形???????????????????????????????????????等腰三角形等边三角形???????????????????????????????????底边和腰不相等的等腰三角形
2)三角形按角分类:三角形直角三角形??????????????????斜三角形锐角三角形钝角三角形
?
三角形的稳定性: 三角形三条边的长度确定之后,三角形的形状就唯一确定了.
?
考点剖析
考点二 三角形的概念及性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}重要线段
概念
图形
性质
三角形的高
从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高).
∵AD是?ABC中BC边的高
∴∠ADB=∠ADC=90°
三角形的中线
在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线
∵AD是?ABC中BC边的中线
∴BD=CD S△ABD=S△ADC
三角形的角平分线
三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线.
∵AD是?ABC中∠BAC的角平分线
∴∠BAD=∠DAC=∠BAC
考点剖析
考点二 三角形的概念及性质
三角形三边关系定理:三角形的两边之和大于第三边.
推论:三角形的两边之差小于第三边.
三角形的内角和定理:三角形三个内角和等于180°.
推论:直角三角形的两个锐角互余.
三角形的内角和定理的应用:
1)在三角形中,已知两个内角的度数,可以求出第三个内角的度数;
2)在三角形中,已知三个内角的比例关系,可以求出三个内角的度数;
3)在直角三角形中,已知一个锐角的度数,可以求出另一个锐角的度数.
三角形的外角和定理:三角形的外角和等于360°.
三角形的外角和的性质:1)三角形的一个外角等于和它不相邻的两个内角的和;
2)三角形的一个外角大于任何一个和它不相邻的内角.
常用技巧或结论
三角形的稳定性解题技巧:
1)当三角形三条边的长度确定之后,三角形的形状就唯一确定了.
2)四边形及多边形不具有稳定性,要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了.
三角形三边关系定理及推论的应用:
1)判断三条已知线段能否组成三角形,只需检验最短的两边之和大于第三边,则可说明能组成三角形.
2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b
3)所有通过周长相加减求三角形的边,求出两个答案的,要注意检查每个答案能否组成三角形.
热考题型
考点二 三角形的概念及性质
1.(23-24七年级上·山东烟台·期中)如图所示的五边形边框,木匠师傅至少需要再钉 根木条才能使其不变形.
2.(22-23七年级下·山东枣庄·期末)如图,????????,????????,????????分别是△????????????的中线、角平分线、高线,下列结论中错误的是(????)
A.????????=12???????? B.2∠????????????=∠????????????
C.∠????+∠????????????=90° D.????????=????????
?
热考题型
考点二 三角形的概念及性质
3.(23-24七年级下·湖北咸宁·期中)如图,直线????∥????,????????与????,????分别相交于点????,????,且????????⊥????????,????????交直线????于点????.
(1)若∠1=60°,求∠2的度数;
(2)若????????=5,????????=12,????????=13,求点????到直线????的距离.
?
【详解】(1)解:∵直线????∥????,
∴∠3=∠1=60°,
又∵????????⊥????????,
∴∠2=90°?∠3=30°;
(2)如图,过????作????????⊥????????于????,则????????的长即为直线????与????的距离.
∵????△????????????=12×????????×????????=12×????????×????????,
∴????????=????????×????????????????=12×513=6013,
∴点????到直线????的距离为6013.
?
热考题型
考点二 三角形的概念及性质
4.(23-24七年级下·福建泉州·期中)如图,在△????????????中,????????是中线,????????=10cm,????????=6cm.
(1)△????????????与△????????????的周长差为_______cm.
(2)点E在边????????上,连接????????,若三角形????????????的周长被????????分成的两部分的差是2cm,求线段????????的长.
?
【详解】(1)解:△????????????的周长=????????+????????+????????,△????????????的周长=????????+????????+????????,
∵????????是中线,∴????????=????????,
△????????????与△????????????的周长差:????????+????????+?????????????????+????????+????????=?????????????????=4cm
?
(2)解:由图可知:△????????????的周长=????????+????????+????????,四边形????????????????的周长=????????+????????+????????+????????,
①当△????????????的周长-四边形????????????????的周长=2cm时,
∵????是????????的中点,∴????????=????????,
∴????????+????????+?????????????????+????????+????????+????????=2,
∴????????=????????+????????+2,
又∵????????=10cm,????????=6cm,????????=?????????????????,
∴????????+????????+2=?????????????????,
∴10?????????=????????+6+2???∴????????=1cm;
?
热考题型
考点二 三角形的概念及性质
4.(23-24七年级下·福建泉州·期中)如图,在△????????????中,????????是中线,????????=10cm,????????=6cm.
(1)△????????????与△????????????的周长差为_______cm.
(2)点E在边????????上,连接????????,若三角形????????????的周长被????????分成的两部分的差是2cm,求线段????????的长.
?
②四边形????????????????的周长-当△????????????的周长=2cm时,
∵????是????????的中点,
∴????????=????????,
∴????????+????????+????????+?????????????????+????????+????????=2,
∴????????+????????=????????+2,
又∵????????=10cm,????????=6cm,????????=?????????????????,
∴????????+????????=?????????????????+2,
∴????????+6=10?????????+2
∴????????=3cm;
综上,线段????????的长为1cm或3cm.
?
热考题型
考点二 三角形的概念及性质
5.(23-24七年级下·广东深圳·期中)已知△????????????的三边长为a,b,c,且a,b,c都是整数.
(1)若????=2,????=5,且c为偶数.求△????????????的周长.
(2)化简:?????????+???????????????????+????+????+????.
?
【详解】(1)解:∵????=2,?????=5,
∴5?2由于c是偶数,则????=4或6,
当????=4时,△????????????的周长为????+????+????=2+5+4=11,
当????=6时,△????????????的周长为????+????+????=2+5+6=13.
综上所述,△????????????的周长为11或13.
(2)解:∵△????????????的三边长为a,b,c,∴????+????>????,
∴|?????????+????|?|??????????????|+|????+????+????|
=????+??????????(????+?????????)+????+????+????
=????+????+????.
?
热考题型
考点二 三角形的概念及性质
6.(23-24七年级下·全国·课后作业)在△????????????中,????????=2cm,????????=9cm.
(1)求第三边????????长的取值范围;
(2)若第三边????????的长是偶数,求????????的长;
(3)若△????????????是等腰三角形,求其周长.
?
【详解】(1)解:∵在△????????????中,????????=2cm,????????=9cm,
∴?????????????????∴9?2cm(2)解:∵7cm∴第三边????????的长为8cm或10cm;
(3)解;∵7cm∴只能是????????=????????=9cm,
∴△????????????的周长为9+9+2=20cm.
?
热考题型
考点二 三角形的概念及性质
热考题型
考点二 三角形的概念及性质
8.(23-24八年级上·湖北武汉·阶段练习)已知:等腰三角形的三边长分别为3?????2,2?????1,????+3,求这个三角形的底边长.
?
【详解】解:①当3?????2是底边时,2?????1=????+3,解得:????=4,
∴2?????1=????+3=4+3=7,3?????2=3×4?2=10,
此时三边为:7,7,10,7?7<10<7+7,满足三边关系,故底边为:10,
②当????+3是底边时,2?????1=3?????2,解得:????=1,
∴2?????1=3?????2=3×1?2=1,????+3=1+3=4,
此时三边为:1,1,4,1?1<4>1+1,不满足三边关系,此类情况不存在,
③当2?????1是底边时,????+3=3?????2,解得:????=52,
∴????+3=3?????2=3×52?2=112,2?????1=2×52?1=4,
此时三边为:112,112,4,112?112<4<112+112,
满足三边关系,故底边为:4,
综上所述:底边为4或10.
?
热考题型
考点二 三角形的概念及性质
9.(22-23七年级下·黑龙江哈尔滨·期中)如图是10×8的网格,网格中每个小正方形的边长均为1,△????????????的三个顶点A、B、C都在小正方形的顶点上,请在图中分别按要求画图:
(1)在图中画△????????????的中线????????;
(2)在图中画△????????????的高线????????.
(3)直接写出△????????????的面积是________.
?
(3)解:????△????????????=12×8×2=8,
?
热考题型
考点二 三角形的概念及性质
10.(22-23七年级上·山东威海·期末)如图,将△????????????沿着????????对折,点A落到????′处,若∠????????????′+∠????????????′=82°,则∠????= ??度.
?
【详解】解:∵将△????????????沿着????????对折,A落到????′,
∴∠????????????=∠????′????????,∠????????????=∠????′????????,
∴∠????????????′+2∠????????????=180°,∠????′????????+2∠????????????=180°,
∴∠????????????′+2∠????????????+∠????′????????+2∠????????????=360°,
∵∠????????????′+∠????????????′=82°,
∴∠????????????+∠????????????=139°,
∴∠????=180°?∠????????????+∠????????????=180°?139°=41°,
?
11.(22-23七年级下·四川成都·期末)若直角三角形的一个锐角等于40°,则它的另一个锐角等于(????)
A.50° B.60° C.70° D.140°
?
热考题型
考点二 三角形的概念及性质
12.(22-23七年级下·广西河池·阶段练习)(1)如图1,已知????????∥????????,点E在两平行线的内侧,连接????????,????????.若∠????????????=35°,∠????????????=25°,求∠????????????的度数;
(2)如图2,已知????????∥????????,点E在两平行线的外侧,连接????????,????????,若∠????????????=????,∠????????????=????.
①求∠????????????的大小(用含α,β的代数式表示);
②作∠????????????的平分线交????????于点G,连接????????,????????平分∠????????????(如图3).若∠????????????=130°,????+????=80°,分别求出α,β的度数.
?
【详解】解:(1)如图1,过点E作????????∥????????.
∵????????∥????????,∴∠????????????=∠????????????=35°.
∵????????∥????????,????????∥????????,
∴????????∥????????.
∴∠????????????=∠????????????=25°.
∴∠????????????=∠????????????+∠????????????=35°+25°=60°.
?
热考题型
考点二 三角形的概念及性质
12.(22-23七年级下·广西河池·阶段练习)(1)如图1,已知????????∥????????,点E在两平行线的内侧,连接????????,????????.若∠????????????=35°,∠????????????=25°,求∠????????????的度数;
(2)如图2,已知????????∥????????,点E在两平行线的外侧,连接????????,????????,若∠????????????=????,∠????????????=????.
①求∠????????????的大小(用含α,β的代数式表示);
②作∠????????????的平分线交????????于点G,连接????????,????????平分∠????????????(如图3).若∠????????????=130°,????+????=80°,分别求出α,β的度数.
?
(2)①∵????????∥????????,
∴∠????????????=∠????????????=????.
又∵∠????????????=∠????????????+∠????????????,∠????????????=????,
∴∠????????????=∠?????????????∠????????????=?????????.
?
热考题型
考点二 三角形的概念及性质
12.(22-23七年级下·广西河池·阶段练习)(1)如图1,已知????????∥????????,点E在两平行线的内侧,连接????????,????????.若∠????????????=35°,∠????????????=25°,求∠????????????的度数;
(2)如图2,已知????????∥????????,点E在两平行线的外侧,连接????????,????????,若∠????????????=????,∠????????????=????.
①求∠????????????的大小(用含α,β的代数式表示);
②作∠????????????的平分线交????????于点G,连接????????,????????平分∠????????????(如图3).若∠????????????=130°,????+????=80°,分别求出α,β的度数.
?
②如图3,
∵????????∥????????,∴∠1=∠2.
又∵????????平分∠????????????,∴∠????????????=∠1=12????.∴∠????????????=∠2.
∵????????平分于∠????????????,∴∠2=∠3.∴∠3=∠????????????=12????.
∵∠????????????=130°,∴∠????????????+∠3=180°?∠????????????=50°.
∴????+12????=50°.又∵????+????=80°,
∴????=20°,????=60°.
?
热考题型
考点二 三角形的概念及性质
13.(23-24七年级下·山东泰安·期中)将一副直角三角板????????????和????????????如图放置(其中∠????=60°,∠????=45°),使点E落在????????边上,且????????∥????????.求∠????????????的度数.
?
【详解】解:∵∠????=∠????=90°,∠????=60°,∠????=45°,
∴ ∠????????????=90°?∠????=30°,∠????????????=90°?∠????=45°,
∵ ????????∥????????,
∴ ∠????????????=∠????????????=30°,
∴ ∠????????????=∠?????????????∠????????????=15°,
∴ ∠????????????=180°?∠????????????=165°.
?
考点剖析
考点三 图形的平移
平移的概念:在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.平移不改变图形的形状和大小.
平移的三大要素:1)平移的起点,2)平移的方向,3)平移的距离.
作图步骤:
1)根据题意,确定平移的方向和平移的距离;
2)找出原图形的关键点;
3)按平移方向和平移距离平移各个关键点,得到各关键点的对应点;
4)按原图形依次连接对应点,得到平移后的图形.
平移的性质:
1)平移不改变图形的大小、形状,只改变图形的位置,因此平移前后的两个图形全等.
2)平移前后对应线段平行且相等、对应角相等.
3)任意两组对应点的连线平行(或在同一条直线上)且相等,对应点之间的距离就是平移的距离.
热考题型
考点三 图形的平移
1.(21-22七年级下·江苏扬州·阶段练习)下列现象:①荡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动.其中属于平移的是(?????)
A.①② B.①③ C.②③ D.②④
热考题型
考点三 图形的平移
3.(23-24七年级上·山东滨州·期末)如图,在三角形????????????中,????????⊥????????,垂足为????,????????=5,将三角形????????????沿射线????????的方向向右平移后,得到三角形????′????′????′,连接????′????,若????????′=12,????′????=4,则三角形????′????????′的面积为 .
?
【详解】解:由平移可知????????=????′????′,
∵????′????=????????+????′????′?????????′,即4=????????+????′????′?12,
∴????????=????′????′=8,
∴????????′=????′????′?????′????=4,
∴????△????′????????′=12????????′?????????=12×4×5=10.
故答案为:10.
?
热考题型
考点三 图形的平移
4.(23-24七年级上·吉林长春·期末)如图,边长为10cm的正方形????????????????先向上平移5cm,再向右平移2cm,得到正方形????′????′????′????′,此时阴影部分的面积为 cm2.
?
【详解】解:如图,
由平移得:????????=5cm,????′????=2cm,????′????′=????????=10cm,
∴????′????=10?2=8cm,????????=10?5=5cm,
即阴影部分是长为8cm,宽为5cm的长方形,
∴阴影部分的面积为8×5=40 cm2,
故答案为:40.
?
热考题型
考点三 图形的平移
5.(22-23七年级下·贵州遵义·期中)如图,某公园有一块长方形地,准备在长方形地内修筑同样宽的小路(图中阴影部分),余下部分进行绿化,已知小路的宽均为2m,则绿化带的面积是 .
?
【详解】解:由平移的性质可将绿化面积转化为长为40?4=36m,宽为30?2=28m的长方形,
∴除去小路,绿化带的面积为36×28=1008m2,
故答案为:1008m2.
?
热考题型
考点三 图形的平移
6.(22-23七年级下·甘肃陇南·期末)星期天早晨,小刚和爸爸正在商量往楼梯上铺地毯的事,如图所示,
爸爸:“小刚,你帮我算一下,从一层铺到二层需要地毯几米?”
小刚:“我早已用盒尺量好了,每阶高15cm,宽为20cm??…”
爸爸:(打断小刚的话)“不量每阶的高度和宽度,你想想有没有办法?”
小刚:(思索)“有了,只需要量出楼梯的总高和总长度再相加,就行了.”
你认为小刚的方法可以吗?说明理由.
?
【详解】解:可以,
如图所示:根据图示可得:
地毯的总长度=????????+????????=15×9+20×9=15+20×9=315cm=3.15m.
?
考点剖析
考点四 多边形的内角和与外角和
多边形的定义:在平面中,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
多边形的对角线:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.?
多边形内角和定理:n边形的内角和为(n?2)?180°(n≥3).
多边形外角和定理:任意多边形的外角和等于360°,与多边形的形状和边数无关.
正多边形的定义:各角相等,各边相等的多边形叫做正多边形.
解题技巧
考点四 多边形的内角和与外角和
1)正n边形的每个内角为(n?2)×180°????,每一个外角为360°????.
2)正n边形有n条对称轴.
3)对于正n边形,当n为奇数时,是轴对称图形;当n为偶数时,既是轴对称图形,又是中心对称图形.
4)从n边形的一个顶点可以引(n-3)条对角线,并且这些对角线把多边形分成了(n–2)个三角形,n边形的对角线条数为????(?????3)2?
?
解题技巧
考点四 多边形的内角和与外角和
1)n边形的内角和随边数的增加而增加,边数每增加1,内角和增加180°.
2)任意多边形的内角和均为180°的整数倍.
3)利用多边形内角和定理可解决三类问题:
①已知多边形的边数求内角和;
②已知多边形的内角和求边数;
③已知足够的角度条件下求某一个内角的度数.
热考题型
考点四 多边形的内角和与外角和
1.(23-24七年级上·贵州毕节·期末)若从多边形的一个顶点出发,最多可引3条对角线,则这个多边形的对角线共有(????)
A.6条 B.9条 C.12条 D.18条
2.(23-24九年级上·四川绵阳·期末)从十二边形的一个顶点引对角线,可把这个多边形分成(????)个三角形.
A.10 B.11 C.12 D.13
3.(22-23七年级下·广东惠州·开学考试)一个多边形的内角和是720°,则这个多边形的边数是
?
6
?
4(22-23七年级下·甘肃天水·期末)如图,小明在操场上从????点出发,沿直线前进8米后向左转40°,再沿直线前进8米后,又向左转40°,这样走下去,他第一次回到出发地????点时,一共走了(????)米
A.56 B.64 C.80 D.72
?
热考题型
考点四 多边形的内角和与外角和
5.(22-23七年级上·湖北武汉·阶段练习)一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是( )
A.9 B.10 C.8或9或10 D.9或10或11
【详解】解:设内角和为1440°的多边形的边数是n,则(n-2)?180=1440,解得:n=10.
∵截去一个角后边上可以增加1,不变,减少1,∴原多边形的边数是9或10或11.故选:D.
【解题技巧】一个n变形剪去一个角后,若剪去的一个角只经过一个顶点和一边,则剩下的形状是n边形,若剪去的一个角经过两条邻边,则剩下的形状是(n+1)边形,若剪去的一个角经过两个相邻点,则剩下的形状是(n-1)边形.所以遇到相关题目时,要分类讨论.
热考题型
考点四 多边形的内角和与外角和
6.(22-23七年级下·福建泉州·期末)正四边形与其他正多边形组合可以铺设地板,则该多边形可以是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
【详解】解:A.正五边形每个内角108°,正四边形每个内角90°,显然不能组合成360°,所以不能铺设地板,不符合题意;
B.正六边形每个内角120°,正四边形每个内角90°,不能组合成360°,所以不能铺设地板,不符合题意;
C.正四边形每个内角90°,正八边形每个内角135°,90°+135°×2=360°,所以能铺设地板,符合题意;
D.因为十边形的每个内角是144°,正四边形的每个内角是90°,不能组合成360°,所以不能铺设地板,不符合题意;故选:C.
?
【解题技巧】解决几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.
热考题型
考点四 多边形的内角和与外角和
7.(22-23七年级下·四川眉山·期中)如图,则∠????+∠????+∠????+∠????+∠????+∠????的度数为( )
A.180° B.360° C.540° D.720°
?
【详解】解:如图,连接????????,
由三角形外角的性质可得:∠1=∠????+∠????=∠????????????+∠????????????,
∴∠????????????+∠????+∠????+∠????+∠????+∠????=∠????????????+∠????????????+∠????????????+∠????????????+∠????+∠????
=∠????????????+∠????????????+∠????+∠????
=360°
故选:B.
?
热考题型
考点四 多边形的内角和与外角和
8.(22-23七年级下·河南南阳·期末)已知一个正n边形的内角和是它的外角和的2倍.
(1)求n;
(2)求正n边形每个内角的度数;
(3)用足够多边长相等的这种正n边形和正三角形两种地板镶嵌地面,则一个顶点处需要此正n边形和正三角形的地板块数分别为:__________.
【详解】(1)解:根据题意得:180°?????2=2×360°,
解得????=6.
答:n的值为6.
(2)解:180°?????26=720°6=120°.
答:正n边形每个内角的度数为120°.
?
热考题型
考点四 多边形的内角和与外角和
8.(22-23七年级下·河南南阳·期末)已知一个正n边形的内角和是它的外角和的2倍.
(1)求n;
(2)求正n边形每个内角的度数;
(3)用足够多边长相等的这种正n边形和正三角形两种地板镶嵌地面,则一个顶点处需要此正n边形和正三角形的地板块数分别为:__________.
(3)解:设在平面镶嵌时,围绕在某一点有x个正六边形和y个正三角形的内角可以拼成一个周角,
根据题意可得:120????+60????=360,即:2????+????=6,
∴????=2????=2或????=1????=4
∴一个顶点处需要此正六边形和正三角形的地板块数分别为:2个,2个或1个,4个.
故答案为: 2个,2个或1个,4个.
?
热考题型
考点四 多边形的内角和与外角和
9.(22-23七年级下·江苏苏州·期末)苏州博物馆本馆是国内唯一一座由世界著名建筑大师贝聿铭亲自设计的博物馆,几何形构造的屋顶颇具特色,粉墙黛瓦的传统元素随处可见,现代主义建筑与苏州园林的有机结合,如同姑苏城里一幅旖旎烟雨交织而成的水墨画.图①中的屋顶设计是在传统飞檐翘角基础上演变而来,呈现出强烈的几何感和抽象性,图②中∠1=∠4=116°,∠2=∠3=90°,则下列判断中正确的是(????)
A.∠5=42° B.∠5=52° C.∠5=62° D.∠5的度数无法确定
?
【详解】解:由题意得五边形的内角和为(5?2)×180°=540°,
∵∠1=∠4=116°,∠2=∠3=90°,
∴∠5=180°?(540°?116°?116°?90°?90°)
=180°?128°
=52°,
故选:B.
?
热考题型
考点四 多边形的内角和与外角和
10.(22-23七年级下·湖北孝感·期中)某自然保护区给一些小动物搭建了小木屋,其侧面如图,????????,????????均与地面垂直,小亮看见了也想回家给自己的小狗做一个同样的小木屋,他用量角器测出∠????=123°,∠????=135°.由于小亮个子太矮,屋顶的∠????测不到,哥哥看到后说,不用测量,我也能算出∠????,你知道哥哥是怎样算出∠????的吗?请你帮哥哥算出∠????的度数是 .
?
【详解】根据题意可知∠????????????=∠????????????=90°,多边形????????????????????为五边形,其内角和为180°×5?2=540°,
可得∠????=540°?∠?????∠?????∠?????????????∠????????????=102°.
故答案为:102°.
?
热考题型
考点四 多边形的内角和与外角和
11.(22-23七年级下·江苏扬州·期末)如图,将透明直尺叠放在正五边形徽章????????????????????上,若直尺的下沿????????⊥????????于点O,且经过点B,上沿????????经过点E,则∠????????????的度数为( )
A.152° B.126° C.120° D.108°
?
【详解】解:由题意可得∠????????????=∠????=5?2×180°÷5=108°,
∵????????⊥????????,
∴∠????????????=90°,
∴四边形????????????????中,∠????????????=360°?90°?108°?108°=54°,
∴∠????????????=180°?∠????????????=180°?54°=126°,
故选:B.
?
热考题型
考点四 多边形的内角和与外角和
12.(21-22七年级上·河南信阳·期末)如图,正五边形????????????????????,????????平分∠????????????,????????平分正五边形的外角∠????????????,则∠????=(????)
A.45° B.54° C.60° D.64°
?
【详解】∵正五边形外角和为360°,
∴外角∠????????????=360°5=72°,
∴内角∠????????????=∠????=∠????????????=180°?72°=108°,
∵????????平分∠????????????,????????平分正五边形的外角∠????????????,
∴∠????????????=12∠????????????=54°, ∠????????????=12∠????????????=36°,
在四边形??????????????中,∠????????????+∠????+∠????????????+∠????????????+∠????=360°,
∴∠????=360°?∠????????????+∠????+∠????????????+∠????????????=360°?54°+108°+108°+36°=54°,
故选:B.
同课章节目录
