专题04 反比例函数(复习课件 共40张PPT)-八年级数学下学期期末考点大串讲(苏科版)
文档属性
| 名称 | 专题04 反比例函数(复习课件 共40张PPT)-八年级数学下学期期末考点大串讲(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 19:28:26 | ||
图片预览










文档简介
八年级苏科版数学下册期末考点大串讲
串讲04 反比例函数
01
02
目
录
考点剖析
考点透视
四大常考点思维导图梳理
四大考点知识梳理+易错易混+热考题型
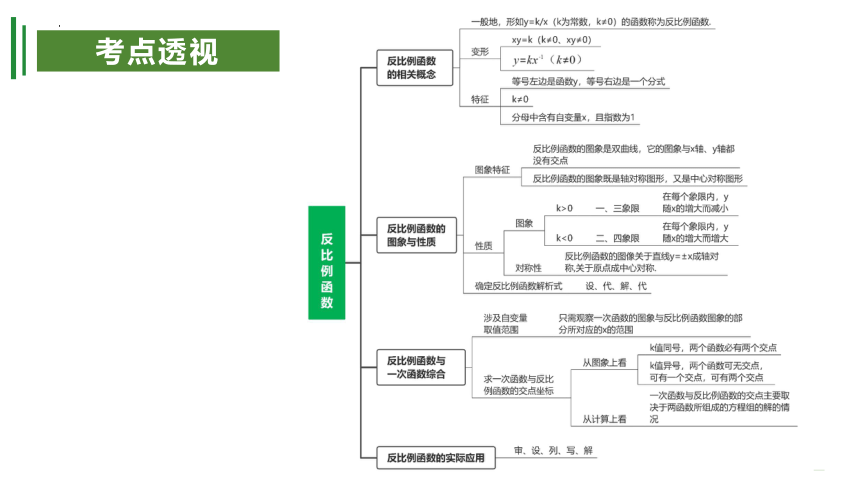
考点透视
考点剖析
考点一 反比例函数的基础
反比例函数的概念:一般地,形如y=kx(k为常数,k≠0)的函数称为反比例函数.反比例函数的解析式也可以写成xy=k(k≠0、xy≠0)、y=kx?1(k≠0)的形式.
反比例函数解析式的特征:
①等号左边是函数y,等号右边是一个分式;
②k≠0;
③分母中含有自变量x,且指数为1.
?
易错易混
考点一 反比例函数的基础
1. 反比例函数????=????????(????≠0)的自变量????的取值为一切非零实数,函数????的取值是一切非零实数.
2. 反比例函数的表达式中,分子是不为零的常数k,分母不能是多项式,只能是x的一次单项式.
3. 反比例函数图象上的点的横纵坐标之积是定值k.
?
热考题型
考点一 反比例函数的基础
1.(22-23八年级下·江苏徐州·阶段练习)下列函数表达式中,表示????是????的反比例函数的有(????)
(1)????=????4;(2)????=34????;(3)?????????=3;(4)????=?3?????1;(5)????=2????+1;(6)????=5????+2
A.1个 B.2个 C.3个 D.4个
?
【详解】解:(1)????=????4不符合反比例函数的形式,是正比例函数;
(2)????=34????可变形为????=34????,符合反比例函数的形式,是反比例函数;
(3)因为?????????=3,所以????≠0,????≠0,?????????=3可变形为????=?3????,符合反比例函数的形式,是反比例函数;
(4)????=?3?????1可变形为????=?3????,符合反比例函数的形式,是反比例函数;
(5)????=2????+1不符合反比例函数的形式,不是反比例函数;
(6)????=5????+2不符合反比例函数的形式,不是反比例函数.
综上所述,是反比例函数的为(2)(3)(4)共3个.
故选:C.
?
热考题型
考点一 反比例函数的基础
2.(22-23八年级下·江苏宿迁·期末)下列各点与点?3,?6在同一个反比例函数图像的是( )
A.?1,?8 B.?2,?9 C.?4,?5 D.?5,?10
3(2022·江苏南京·校联考一模)已知反比例函数y=????????的图象经过点(1,3)、(m,n),则mn的值为 .
?
【详解】解:把点(1,3)代入y=????????得k=3
故反比例函数的解析式为????=3????
把点(m,n)代入????=3???? 得mn=3故答案为:3
?
热考题型
考点一 反比例函数的基础
4(2022上·山东枣庄·九年级校考期末)已知函数????=(????+1)????????2?5是关于????的反比例函数,则????的值是 .
?
【详解】∵函数????=(????+1)????????2?5是关于????的反比例函数,
∴????+1≠0,????2?5=?1,
∴????=±2,
?
5.(2023·北京朝阳·统考一模)下面的三个问题中都有两个变量:
①矩形的面积一定,一边长????与它的邻边????;②某村的耕地面积一定,该村人均耕地面积????与全村总人口????;③汽车的行驶速度一定,行驶路程????与行驶时间????.
其中,两个变量之间的函数关系可以用如图所示的图象表示的是(????)
A.①② B.①③ C.②③ D.①②③
?
热考题型
考点一 反比例函数的基础
6.(22-23七年级下·四川成都·期中)根据所学函数知识,解答下列问题:
(1)已知函数????=????+2?????????1+????+4,当????,????为何值时,此函数是一次函数?
(2)当????为何值时,函数????=????+3?????????4是反比例函数,并求当????=3时,????的值为多少?
?
【详解】(1)∵函数????=????+2?????????1+????+4是一次函数,
∴????+2≠0?????1=1且????+4为任意实数,
解得????=2,
∴????=2,????为任意实数;
(2)∵函数????=????+3?????????4是反比例函数,
∴????+3≠0?????4=?1,解得????=3,
∴反比例函数的解析式为????=6????,
∴当????=3时,6????=3,∴????=2.
?
热考题型
考点一 反比例函数的基础
7.(22-23八年级下·江苏扬州·期末)已知y与?????1成反比例,并且当????=3时,????=4.则y与x之间的函数解析式为 .
?
【详解】解:由题知,令????=?????????1,
又当????=3时,????=4,
则????3?1=4,解得????=8.
所以y与x之间的函数解析式为:????=8?????1.
故答案为:????=8?????1.
?
考点剖析
考点二 反比例函数的图象与性质
{5940675A-B579-460E-94D1-54222C63F5DA}?
?
图象特征
1)反比例函数的图象是双曲线,它有两个分支,它的图象与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴.
2)反比例函数的图象既是轴对称图形,又是中心对称图形,其对称轴为直线y=±x,对称中心为原点.
?
?
?
?
?
?
性质
表达
式
(为常数,)
?
?
图象
?
?
?
?
?
?
k>0
k<0
经过
象限
一、三象限(x、y同号)
二、四象限(x、y异号)
考点剖析
考点二 反比例函数的图象与性质
{5940675A-B579-460E-94D1-54222C63F5DA}
性质
增减性
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
?
对称性
①图象关于原点对称,即若(a,b)在双曲线的一支上,则(-a,-b)在双曲线的另一支上;
②图象关于直线 对称,即若(a,b)在双曲线的一支上,则(b,a)在双曲线的另一支上;
③图象关于直线对称,即若(a,b)在双曲线的一支上,则(-b,-a)在双曲线的另一支上.
即:反比例函数的图象关于直线y=±x成轴对称,关于原点成中心对称.
反比例函数解析式的确定方法
待定系数法求反比例函数解析式的一般步骤:
1)设反比例函数的解析式为(k为常数,k≠0);
2)把已知的一对x,y的值带入解析式,得到一个关于待定系数k的方程;
3)解方程求出待定系数k;
4)将所求的k值代入所设解析式中.
【说明】由于在反比例函数中,只有一个待定系数,因此只需要一对对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.
易错易混
考点二 反比例函数的图象与性质
1. 反比例函数的图象不是连续的,因此在描述反比例函数的增减性时,一定要有“在其每个象限内”这个前提.当k>0时,在每一象限(第一、三象限)内y随x的增大而减小,但不能笼统地说当k>0时,y随x的增大而减小.同样,当k<0时,也不能笼统地说y随x的增大而增大.
2. 反比例函数图象的位置和函数的增减性,都是由常数k的符号决定的,反过来,由双曲线所在位置和函数的增减性,也可以推断出k的符号。
3. 双曲线是由两个分支组成的,一般不说两个分支经过第一、三象限(或第二、四象限),而说图象的两个分支分别在第一、三象限(或第二、四象限).
热考题型
考点二 反比例函数的图象与性质
1.(23-24八年级上·上海青浦·期中)反比例函数????=?4????,下列说法不正确的是(????)
A.图像经过点(1,?4) B.图像位于第二、四象限
C.图像关于直线????=????对称 D.函数值y图像随x增大而减小
?
【详解】A、????=1时,????=?4,故图象经过点(1,?4),正确;
B、????<0,图象位于二、四象限,故正确;
C、反比例函数的图象关于直线????=????对称,故正确;
D、∵????<0,∴图象位于二、四象限,在每一象限内y随x的增大而证得,故错误;
故选:D.
?
热考题型
考点二 反比例函数的图象与性质
2.(22-23八年级下·江苏扬州·期末)若点????2,????1,????????,????1+1在反比例函数????=????2????(????≠0)的图像上,则m满足(???)
A.????>2 B.02
?
【详解】解:在反比例函数????=????2????(????≠0)中,
∵????=????2>0,
∴反比例函数????=????2????(????≠0)的图象在第一、三象限,在每个象限内,????随????的增大而减小,
∵点????(2,????1)、????(????,????1+1)在反比例函数????=????2????(????≠0)的图象上,且0∴0故选:B.
?
热考题型
考点二 反比例函数的图象与性质
3.(22-23九年级上·湖南长沙·阶段练习)在平面直角坐标系????????????中,若反比例函数????=?????2022????的图象位第二、四象限,则k的取值范围是 .
?
【详解】解:∵反比例函数????=?????2022????的图象位第二、四象限,
∴?????2022<0,解得????<2022,
?
4.(22-23八年级下·吉林长春·期中)已知反比例函数????=2????,当4≤????≤10时,y的最大值为 .
?
【详解】解:当4≤????≤10时,反比例函数????=2????的图象随????的增大而减小,
则????在????=4时取得最大值,????=12.
故答案为:12.
?
热考题型
考点二 反比例函数的图象与性质
5.(22-23八年级下·江苏苏州·期末)若反比例函数????=(????+1)????3?????2的图象在每个象限内随着????的增大而增大,则????的值为 .
?
【详解】解:∵反比例函数????=(????+1)????3?????2的图象在每个象限内随着x的增大而增大,
∴????+1<0且3?????2=?1,
解得????=?2.故答案为:?2.
?
6.(22-23八年级下·江苏苏州·阶段练习)若点????????1,????1、????????2,????2在函数????=12????的图象上,且????1”).
?
【详解】解:∵反比例函数????=12????中的12>0,
∴该函数图象位于第一、三象限,且在每一象限内y随x的增大而减小.
∵????1∴????1>????2.
故答案为:>.
?
热考题型
考点二 反比例函数的图象与性质
7.(22-23八年级下·江苏镇江·阶段练习)已知点????,????为反比例函数????=4????图像上的一点,若?4?
【详解】解:在反比例函数????=4????中,????=4>0,
∴函数图象在第一、三象限,且在每个象限内????随着????的增大而减小,
当?4当01,
综上,????的取值范围是????1.
故答案为:????1.
?
热考题型
考点二 反比例函数的图象与性质
8.(22-23九年级上·全国·单元测试)已知函数????=?????5????????≠5.
(1)在什么条件下,函数的图象分布在第一、第三象限?在什么条件下,函数的图象分布在第二、第四象限?
(2)在什么条件下,????随????的增大而减小?在什么条件下,????随????的增大而增大?
?
【详解】(1)解:∵函数????=?????5????????≠5的图象分布在第一、第三象限,
∴?????5>0,∴????>5;
∵函数????=?????5????????≠5的图象分布在第二、第四象限,
∴?????5<0,∴????<5;
?
热考题型
考点二 反比例函数的图象与性质
8.(22-23九年级上·全国·单元测试)已知函数????=?????5????????≠5.
(1)在什么条件下,函数的图象分布在第一、第三象限?在什么条件下,函数的图象分布在第二、第四象限?
(2)在什么条件下,????随????的增大而减小?在什么条件下,????随????的增大而增大?
?
(2)解:∵在每一个象限内,函数????=?????5????????≠5随????的增大而减小,
∴?????5>0,∴????>5,
即当????>5时,在每一个象限内,????随????的增大而减小;
∵在每一个象限内,函数????=?????5????????≠5随????的增大而增大,
∴?????5<0,
∴????<5,
即当????<5时,在每一个象限内,????随????的增大而增大.
?
热考题型
考点二 反比例函数的图象与性质
9.(22-23八年级下·吉林长春·期中)如图,已知反比例函数????=????????的图象经过点????2,3.
(1)求k的值.
(2)若点B在x轴上,且????????=????????,则△????????????的面积为______.
?
【详解】(1)解:把????2,3代入到????=????????,得3=????2,
解得,????=6;
(2)如图,过A作????????⊥????????于点C,设点A的坐标为????,????,
设点A的坐标为????,????,
∴????????=6
∵????????⊥????????,????????=????????,
∴????????=2????????,
∴△????????????的面积为12?????????????????=12×2?????????=????????=6,
故答案为:6
?
热考题型
考点二 反比例函数的图象与性质
10.(22-23八年级下·江苏苏州·阶段练习)如图,两个反比例函数????=????????和????=3????在第一象限内的图象依次是????1和????2,设点P在????1上,????????⊥????轴于点C,交????2于点A,????????⊥????轴于点D,交????2于点B,若四边形????????????????的面积为5,求k的值.
?
【详解】∵????????⊥????轴,????????⊥????轴,两个函数图象都在第一象限,
∴????矩形????????????????=????,????△????????????=????△????????????=12×3=1.5,
∴四边形????????????????的面积=????矩形?????????????????????△?????????????????△????????????=?????1.5?1.5=5.
解得????=8.
?
考点剖析
考点三 反比例函数与一次函数综合
1.涉及自变量取值范围
当一次函数与反比例函数相交时,联立两个解析式,构造方程组,然后求出交点坐标.针对y1>y2时自变量x的取值范围,只需观察一次函数的图象高于反比例函数图象的部分所对应的x的范围.例如,如下图,当y1>y2时,x的取值范围为x>xA或xB考点剖析
考点三 反比例函数与一次函数综合
2.求一次函数与反比例函数的交点坐标
1)从图象上看,一次函数与反比例函数的交点由k值的符号来决定.
①k值同号,两个函数必有两个交点;
②k值异号,两个函数可无交点,可有一个交点,可有两个交点;
2)从计算上看,一次函数与反比例函数的交点主要取决于两函数所组成的方程组的解的情况.
热考题型
考点三 反比例函数与一次函数综合
1.(2023九年级·全国·专题练习)如图,在平面直角坐标系????????????中,函数????=????????(其中????<0)的图象经过平行四边形????????????????的顶点A,函数????=8????(其中????>0)的图象经过顶点C,点B在x轴上,若点C的横坐标为2,△????????????的面积为6.
(1)求k的值;
(2)求直线????????的解析式.
?
【详解】(1)解:∵点C的横坐标是2,
∴2????=8,????=4,
∴????2,4,
∵四边形????????????????是平行四边形,
∴??????∥????轴,
∵????△????????????=6,即12×4????????=6,
∴????????=3,
∴????????=3﹣2=,
∴点A的坐标为?????1,4,
∴????=?1×4=?4;
?
热考题型
考点三 反比例函数与一次函数综合
1.(2023九年级·全国·专题练习)如图,在平面直角坐标系????????????中,函数????=????????(其中????<0)的图象经过平行四边形????????????????的顶点A,函数????=8????(其中????>0)的图象经过顶点C,点B在x轴上,若点C的横坐标为2,△????????????的面积为6.
(1)求k的值;
(2)求直线????????的解析式.
?
热考题型
考点三 反比例函数与一次函数综合
2.(22-23九年级上·湖南永州·阶段练习)如图,一次函数????=????1????+????????≠0与反比例函数????=????2????????>0的图像交于????1,6,????3,????两点.
(1)求反比例函数和一次函数的解析式:
(2)根据图象直接写出????1????+????(3)求△????????????的面积.
?
热考题型
考点三 反比例函数与一次函数综合
2.(22-23九年级上·湖南永州·阶段练习)如图,一次函数????=????1????+????????≠0与反比例函数????=????2????????>0的图像交于????1,6,????3,????两点.
(1)求反比例函数和一次函数的解析式:
(2)根据图象直接写出????1????+????(3)求△????????????的面积.
?
(2)由图象得:当03时,????1????+????(3)∵直线????=?2????+8与????轴相交于点????,
∴????的坐标是(0,8).
∴????Δ????????????=????Δ?????????????????Δ????????????=12×8×(3?1)=8.
?
热考题型
考点三 反比例函数与一次函数综合
3.(2023·四川乐山·二模)如图,已知正比例函数????=2????与反比例函数????=????????????≠0的图象都经过点A和点B,点A的横坐标为1,过点A作x轴的垂线,垂足为M,连接????????.
(1)这个反比例函数的解析式;
(2)△????????????的面积.
?
【详解】(1)解:∵点A在正比例函数????=2????的图象上,
∴????=2×1=2,∴????1,2;
又∵点A在反比例函数????=????????????≠0的图象上,
∴2=????1,
解得:????=2,
∴反比例函数的解析式为????=2????;
?
热考题型
考点三 反比例函数与一次函数综合
3.(2023·四川乐山·二模)如图,已知正比例函数????=2????与反比例函数????=????????????≠0的图象都经过点A和点B,点A的横坐标为1,过点A作x轴的垂线,垂足为M,连接????????.
(1)这个反比例函数的解析式;
(2)△????????????的面积.
?
(2)解:∵????1,2,
∴????????=2,????????=1,
∴????△????????????=12×1×2=1,
∴????△????????????=2????△????????????=2.
?
热考题型
考点三 反比例函数与一次函数综合
4.(2023·西藏·模拟预测)如图,已知一次函数????=?????+????的图象与反比例函数????=????????的图象交于????4,?2,?????2,????两点.
(1)请直接写出不等式?????+????≤????????的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点????作????轴的垂线,垂足为????,连接????????,求△????????????的面积.
?
【详解】(1)解:由图象可知,不等式?????+????≤????????的解集为?2≤????<0或????≥4;
(2)解:∵一次函数????=?????+????的图象与反比例函数????=????????的图象交于????(4,?2)、????(?2,????)两点,
∴????=4×?2=?2????,?2=?4+????,
解得????=?8,????=4,????=2,
∴反比例函数和一次函数的解析式分别为????=?8????,????=?????+2;
(3)解:????△????????????=12×2×4+2=6.
?
热考题型
考点三 反比例函数与一次函数综合
5.(2024·内蒙古呼和浩特·模拟预测)如图,在平面直角坐标系中,一次函数????1=????????+????的图象与反比例函数????2=????????的图象交于点????1,????和?????2,?1.
(1)求一次函数和反比例函数的表达式;
(2)请直接写出????1(3)过点B作????????⊥????轴,????????⊥????????于点D,点C是直线????????上一点,若????????=2????????,求点C的坐标.
?
热考题型
考点三 反比例函数与一次函数综合
5.(2024·内蒙古呼和浩特·模拟预测)如图,在平面直角坐标系中,一次函数????1=????????+????的图象与反比例函数????2=????????的图象交于点????1,????和?????2,?1.
(1)求一次函数和反比例函数的表达式;
(2)请直接写出????1(3)过点B作????????⊥????轴,????????⊥????????于点D,点C是直线????????上一点,若????????=2????????,求点C的坐标.
?
(2)不等式????1(3)根据????1,2,?????2,?1,得到?????2,2,设?????2,????,
则????????=?2?12+?????22,????????=2?????,
∵????????=2????????, ∴9+???22=4?????22,
解得????1=2+3,????2=2?3,
故点C的坐标为(?2,2?3)或(?2,2+3).
?
考点剖析
考点四 反比例函数的实际应用
用反比例函数解决实际问题的步骤:
1)审:审清题意,找出题目中的常量、变量,并理清常量与变量之间的关系;
2)设:根据常量与变量之间的关系,设出函数解析式,待定的系数用字母表示;
3)列:由题目中的已知条件列出方程,求出待定系数;
4)写:写出函数解析式,并注意解析式中变量的取值范围;
5)解:用函数解析式去解决实际问题.
利用反比例函数解决实际问题,要做到:
1)能把实际的问题转化为数学问题,建立反比例函数的数学模型;
2)注意在自变量和函数值的取值上的实际意义;
3)问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.
【易错点】
1.利用反比例函数的性质时,误认为所给出的点在同一曲线上;
2.利用函数图象解决实际问题时,容易忽视自变量在实际问题的意义.
热考题型
考点四 反比例函数的实际应用
1.(23-24九年级上·山东济南·期中)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中????????段是恒温阶段,????????段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(1)求????????段反比例函数图象的关系式,并写出自变量x的取值范围;
(2)恒温阶段保持的时间有多少小时?
(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
?
【详解】(1)解:设????????对应函数解析式为????=????????(????≠0),
把????24,10代入????=????????(????≠0)中得:????=24×10=240,
∴????=240????,
当????=20时,20=240????,解得????=12,即????=12;
∴????=240????12?
热考题型
考点四 反比例函数的实际应用
1.(23-24九年级上·山东济南·期中)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中????????段是恒温阶段,????????段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(1)求????????段反比例函数图象的关系式,并写出自变量x的取值范围;
(2)恒温阶段保持的时间有多少小时?
(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
?
(2)解:由(1)知????=12,
∵ ????2,20,
∴恒温阶段保持的时间有:12?2=10(小时),
答:恒温阶段保持的时间有10小时;
?
热考题型
考点四 反比例函数的实际应用
1.(23-24九年级上·山东济南·期中)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中????????段是恒温阶段,????????段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
?
热考题型
考点四 反比例函数的实际应用
2.(23-24八年级下·湖南衡阳·期中)我校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果????(单位:效力)与时间????(单位:分钟)呈现三段函数图象,其中????????段为渐消毒阶段,????????段为深消毒阶段,????????段是反比例函数图象的一部分,为降消毒阶段,请根据图中信息解答下列问题:
(1)第3分钟时消毒效果为________效力;
(2)求深消毒阶段和降消毒阶段中????与????之间的函数关系式;
(3)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
?
【详解】(1)解:由图象可知,第3分钟处于????????段渐消毒阶段,
设渐消毒阶段的函数解析式为????=????????,
将点10,3代入得:10????=3,解得:????=0.3,
∴渐消毒阶段的函数解析式为????=0.3????,
当????=3时,????=0.3×3=0.9,
即第3分钟时消毒效果为0.9效力,
故答案为:0.9
?
热考题型
考点四 反比例函数的实际应用
2.(23-24八年级下·湖南衡阳·期中)我校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果????(单位:效力)与时间????(单位:分钟)呈现三段函数图象,其中????????段为渐消毒阶段,????????段为深消毒阶段,????????段是反比例函数图象的一部分,为降消毒阶段,请根据图中信息解答下列问题:
(2)求深消毒阶段和降消毒阶段中????与????之间的函数关系式;
?
热考题型
考点四 反比例函数的实际应用
2.(23-24八年级下·湖南衡阳·期中)我校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果????(单位:效力)与时间????(单位:分钟)呈现三段函数图象,其中????????段为渐消毒阶段,????????段为深消毒阶段,????????段是反比例函数图象的一部分,为降消毒阶段,请根据图中信息解答下列问题:
(3)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
?
(3)解:当深消毒阶段消毒效果达到4效力时,则0.15????+1.5=4,
解得:????=1623;
当降消毒阶段消毒效果达到4效力时,则4=180????,
解得:????=45,
∵45?1623=2813>28,
即本次消毒有效.
串讲04 反比例函数
01
02
目
录
考点剖析
考点透视
四大常考点思维导图梳理
四大考点知识梳理+易错易混+热考题型
考点透视
考点剖析
考点一 反比例函数的基础
反比例函数的概念:一般地,形如y=kx(k为常数,k≠0)的函数称为反比例函数.反比例函数的解析式也可以写成xy=k(k≠0、xy≠0)、y=kx?1(k≠0)的形式.
反比例函数解析式的特征:
①等号左边是函数y,等号右边是一个分式;
②k≠0;
③分母中含有自变量x,且指数为1.
?
易错易混
考点一 反比例函数的基础
1. 反比例函数????=????????(????≠0)的自变量????的取值为一切非零实数,函数????的取值是一切非零实数.
2. 反比例函数的表达式中,分子是不为零的常数k,分母不能是多项式,只能是x的一次单项式.
3. 反比例函数图象上的点的横纵坐标之积是定值k.
?
热考题型
考点一 反比例函数的基础
1.(22-23八年级下·江苏徐州·阶段练习)下列函数表达式中,表示????是????的反比例函数的有(????)
(1)????=????4;(2)????=34????;(3)?????????=3;(4)????=?3?????1;(5)????=2????+1;(6)????=5????+2
A.1个 B.2个 C.3个 D.4个
?
【详解】解:(1)????=????4不符合反比例函数的形式,是正比例函数;
(2)????=34????可变形为????=34????,符合反比例函数的形式,是反比例函数;
(3)因为?????????=3,所以????≠0,????≠0,?????????=3可变形为????=?3????,符合反比例函数的形式,是反比例函数;
(4)????=?3?????1可变形为????=?3????,符合反比例函数的形式,是反比例函数;
(5)????=2????+1不符合反比例函数的形式,不是反比例函数;
(6)????=5????+2不符合反比例函数的形式,不是反比例函数.
综上所述,是反比例函数的为(2)(3)(4)共3个.
故选:C.
?
热考题型
考点一 反比例函数的基础
2.(22-23八年级下·江苏宿迁·期末)下列各点与点?3,?6在同一个反比例函数图像的是( )
A.?1,?8 B.?2,?9 C.?4,?5 D.?5,?10
3(2022·江苏南京·校联考一模)已知反比例函数y=????????的图象经过点(1,3)、(m,n),则mn的值为 .
?
【详解】解:把点(1,3)代入y=????????得k=3
故反比例函数的解析式为????=3????
把点(m,n)代入????=3???? 得mn=3故答案为:3
?
热考题型
考点一 反比例函数的基础
4(2022上·山东枣庄·九年级校考期末)已知函数????=(????+1)????????2?5是关于????的反比例函数,则????的值是 .
?
【详解】∵函数????=(????+1)????????2?5是关于????的反比例函数,
∴????+1≠0,????2?5=?1,
∴????=±2,
?
5.(2023·北京朝阳·统考一模)下面的三个问题中都有两个变量:
①矩形的面积一定,一边长????与它的邻边????;②某村的耕地面积一定,该村人均耕地面积????与全村总人口????;③汽车的行驶速度一定,行驶路程????与行驶时间????.
其中,两个变量之间的函数关系可以用如图所示的图象表示的是(????)
A.①② B.①③ C.②③ D.①②③
?
热考题型
考点一 反比例函数的基础
6.(22-23七年级下·四川成都·期中)根据所学函数知识,解答下列问题:
(1)已知函数????=????+2?????????1+????+4,当????,????为何值时,此函数是一次函数?
(2)当????为何值时,函数????=????+3?????????4是反比例函数,并求当????=3时,????的值为多少?
?
【详解】(1)∵函数????=????+2?????????1+????+4是一次函数,
∴????+2≠0?????1=1且????+4为任意实数,
解得????=2,
∴????=2,????为任意实数;
(2)∵函数????=????+3?????????4是反比例函数,
∴????+3≠0?????4=?1,解得????=3,
∴反比例函数的解析式为????=6????,
∴当????=3时,6????=3,∴????=2.
?
热考题型
考点一 反比例函数的基础
7.(22-23八年级下·江苏扬州·期末)已知y与?????1成反比例,并且当????=3时,????=4.则y与x之间的函数解析式为 .
?
【详解】解:由题知,令????=?????????1,
又当????=3时,????=4,
则????3?1=4,解得????=8.
所以y与x之间的函数解析式为:????=8?????1.
故答案为:????=8?????1.
?
考点剖析
考点二 反比例函数的图象与性质
{5940675A-B579-460E-94D1-54222C63F5DA}?
?
图象特征
1)反比例函数的图象是双曲线,它有两个分支,它的图象与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴.
2)反比例函数的图象既是轴对称图形,又是中心对称图形,其对称轴为直线y=±x,对称中心为原点.
?
?
?
?
?
?
性质
表达
式
(为常数,)
?
?
图象
?
?
?
?
?
?
k>0
k<0
经过
象限
一、三象限(x、y同号)
二、四象限(x、y异号)
考点剖析
考点二 反比例函数的图象与性质
{5940675A-B579-460E-94D1-54222C63F5DA}
性质
增减性
在每个象限内,y随x的增大而减小
在每个象限内,y随x的增大而增大
?
对称性
①图象关于原点对称,即若(a,b)在双曲线的一支上,则(-a,-b)在双曲线的另一支上;
②图象关于直线 对称,即若(a,b)在双曲线的一支上,则(b,a)在双曲线的另一支上;
③图象关于直线对称,即若(a,b)在双曲线的一支上,则(-b,-a)在双曲线的另一支上.
即:反比例函数的图象关于直线y=±x成轴对称,关于原点成中心对称.
反比例函数解析式的确定方法
待定系数法求反比例函数解析式的一般步骤:
1)设反比例函数的解析式为(k为常数,k≠0);
2)把已知的一对x,y的值带入解析式,得到一个关于待定系数k的方程;
3)解方程求出待定系数k;
4)将所求的k值代入所设解析式中.
【说明】由于在反比例函数中,只有一个待定系数,因此只需要一对对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.
易错易混
考点二 反比例函数的图象与性质
1. 反比例函数的图象不是连续的,因此在描述反比例函数的增减性时,一定要有“在其每个象限内”这个前提.当k>0时,在每一象限(第一、三象限)内y随x的增大而减小,但不能笼统地说当k>0时,y随x的增大而减小.同样,当k<0时,也不能笼统地说y随x的增大而增大.
2. 反比例函数图象的位置和函数的增减性,都是由常数k的符号决定的,反过来,由双曲线所在位置和函数的增减性,也可以推断出k的符号。
3. 双曲线是由两个分支组成的,一般不说两个分支经过第一、三象限(或第二、四象限),而说图象的两个分支分别在第一、三象限(或第二、四象限).
热考题型
考点二 反比例函数的图象与性质
1.(23-24八年级上·上海青浦·期中)反比例函数????=?4????,下列说法不正确的是(????)
A.图像经过点(1,?4) B.图像位于第二、四象限
C.图像关于直线????=????对称 D.函数值y图像随x增大而减小
?
【详解】A、????=1时,????=?4,故图象经过点(1,?4),正确;
B、????<0,图象位于二、四象限,故正确;
C、反比例函数的图象关于直线????=????对称,故正确;
D、∵????<0,∴图象位于二、四象限,在每一象限内y随x的增大而证得,故错误;
故选:D.
?
热考题型
考点二 反比例函数的图象与性质
2.(22-23八年级下·江苏扬州·期末)若点????2,????1,????????,????1+1在反比例函数????=????2????(????≠0)的图像上,则m满足(???)
A.????>2 B.02
?
【详解】解:在反比例函数????=????2????(????≠0)中,
∵????=????2>0,
∴反比例函数????=????2????(????≠0)的图象在第一、三象限,在每个象限内,????随????的增大而减小,
∵点????(2,????1)、????(????,????1+1)在反比例函数????=????2????(????≠0)的图象上,且0∴0故选:B.
?
热考题型
考点二 反比例函数的图象与性质
3.(22-23九年级上·湖南长沙·阶段练习)在平面直角坐标系????????????中,若反比例函数????=?????2022????的图象位第二、四象限,则k的取值范围是 .
?
【详解】解:∵反比例函数????=?????2022????的图象位第二、四象限,
∴?????2022<0,解得????<2022,
?
4.(22-23八年级下·吉林长春·期中)已知反比例函数????=2????,当4≤????≤10时,y的最大值为 .
?
【详解】解:当4≤????≤10时,反比例函数????=2????的图象随????的增大而减小,
则????在????=4时取得最大值,????=12.
故答案为:12.
?
热考题型
考点二 反比例函数的图象与性质
5.(22-23八年级下·江苏苏州·期末)若反比例函数????=(????+1)????3?????2的图象在每个象限内随着????的增大而增大,则????的值为 .
?
【详解】解:∵反比例函数????=(????+1)????3?????2的图象在每个象限内随着x的增大而增大,
∴????+1<0且3?????2=?1,
解得????=?2.故答案为:?2.
?
6.(22-23八年级下·江苏苏州·阶段练习)若点????????1,????1、????????2,????2在函数????=12????的图象上,且????1”).
?
【详解】解:∵反比例函数????=12????中的12>0,
∴该函数图象位于第一、三象限,且在每一象限内y随x的增大而减小.
∵????1∴????1>????2.
故答案为:>.
?
热考题型
考点二 反比例函数的图象与性质
7.(22-23八年级下·江苏镇江·阶段练习)已知点????,????为反比例函数????=4????图像上的一点,若?4?
【详解】解:在反比例函数????=4????中,????=4>0,
∴函数图象在第一、三象限,且在每个象限内????随着????的增大而减小,
当?4当01,
综上,????的取值范围是????1.
故答案为:????1.
?
热考题型
考点二 反比例函数的图象与性质
8.(22-23九年级上·全国·单元测试)已知函数????=?????5????????≠5.
(1)在什么条件下,函数的图象分布在第一、第三象限?在什么条件下,函数的图象分布在第二、第四象限?
(2)在什么条件下,????随????的增大而减小?在什么条件下,????随????的增大而增大?
?
【详解】(1)解:∵函数????=?????5????????≠5的图象分布在第一、第三象限,
∴?????5>0,∴????>5;
∵函数????=?????5????????≠5的图象分布在第二、第四象限,
∴?????5<0,∴????<5;
?
热考题型
考点二 反比例函数的图象与性质
8.(22-23九年级上·全国·单元测试)已知函数????=?????5????????≠5.
(1)在什么条件下,函数的图象分布在第一、第三象限?在什么条件下,函数的图象分布在第二、第四象限?
(2)在什么条件下,????随????的增大而减小?在什么条件下,????随????的增大而增大?
?
(2)解:∵在每一个象限内,函数????=?????5????????≠5随????的增大而减小,
∴?????5>0,∴????>5,
即当????>5时,在每一个象限内,????随????的增大而减小;
∵在每一个象限内,函数????=?????5????????≠5随????的增大而增大,
∴?????5<0,
∴????<5,
即当????<5时,在每一个象限内,????随????的增大而增大.
?
热考题型
考点二 反比例函数的图象与性质
9.(22-23八年级下·吉林长春·期中)如图,已知反比例函数????=????????的图象经过点????2,3.
(1)求k的值.
(2)若点B在x轴上,且????????=????????,则△????????????的面积为______.
?
【详解】(1)解:把????2,3代入到????=????????,得3=????2,
解得,????=6;
(2)如图,过A作????????⊥????????于点C,设点A的坐标为????,????,
设点A的坐标为????,????,
∴????????=6
∵????????⊥????????,????????=????????,
∴????????=2????????,
∴△????????????的面积为12?????????????????=12×2?????????=????????=6,
故答案为:6
?
热考题型
考点二 反比例函数的图象与性质
10.(22-23八年级下·江苏苏州·阶段练习)如图,两个反比例函数????=????????和????=3????在第一象限内的图象依次是????1和????2,设点P在????1上,????????⊥????轴于点C,交????2于点A,????????⊥????轴于点D,交????2于点B,若四边形????????????????的面积为5,求k的值.
?
【详解】∵????????⊥????轴,????????⊥????轴,两个函数图象都在第一象限,
∴????矩形????????????????=????,????△????????????=????△????????????=12×3=1.5,
∴四边形????????????????的面积=????矩形?????????????????????△?????????????????△????????????=?????1.5?1.5=5.
解得????=8.
?
考点剖析
考点三 反比例函数与一次函数综合
1.涉及自变量取值范围
当一次函数与反比例函数相交时,联立两个解析式,构造方程组,然后求出交点坐标.针对y1>y2时自变量x的取值范围,只需观察一次函数的图象高于反比例函数图象的部分所对应的x的范围.例如,如下图,当y1>y2时,x的取值范围为x>xA或xB
考点三 反比例函数与一次函数综合
2.求一次函数与反比例函数的交点坐标
1)从图象上看,一次函数与反比例函数的交点由k值的符号来决定.
①k值同号,两个函数必有两个交点;
②k值异号,两个函数可无交点,可有一个交点,可有两个交点;
2)从计算上看,一次函数与反比例函数的交点主要取决于两函数所组成的方程组的解的情况.
热考题型
考点三 反比例函数与一次函数综合
1.(2023九年级·全国·专题练习)如图,在平面直角坐标系????????????中,函数????=????????(其中????<0)的图象经过平行四边形????????????????的顶点A,函数????=8????(其中????>0)的图象经过顶点C,点B在x轴上,若点C的横坐标为2,△????????????的面积为6.
(1)求k的值;
(2)求直线????????的解析式.
?
【详解】(1)解:∵点C的横坐标是2,
∴2????=8,????=4,
∴????2,4,
∵四边形????????????????是平行四边形,
∴??????∥????轴,
∵????△????????????=6,即12×4????????=6,
∴????????=3,
∴????????=3﹣2=,
∴点A的坐标为?????1,4,
∴????=?1×4=?4;
?
热考题型
考点三 反比例函数与一次函数综合
1.(2023九年级·全国·专题练习)如图,在平面直角坐标系????????????中,函数????=????????(其中????<0)的图象经过平行四边形????????????????的顶点A,函数????=8????(其中????>0)的图象经过顶点C,点B在x轴上,若点C的横坐标为2,△????????????的面积为6.
(1)求k的值;
(2)求直线????????的解析式.
?
热考题型
考点三 反比例函数与一次函数综合
2.(22-23九年级上·湖南永州·阶段练习)如图,一次函数????=????1????+????????≠0与反比例函数????=????2????????>0的图像交于????1,6,????3,????两点.
(1)求反比例函数和一次函数的解析式:
(2)根据图象直接写出????1????+????(3)求△????????????的面积.
?
热考题型
考点三 反比例函数与一次函数综合
2.(22-23九年级上·湖南永州·阶段练习)如图,一次函数????=????1????+????????≠0与反比例函数????=????2????????>0的图像交于????1,6,????3,????两点.
(1)求反比例函数和一次函数的解析式:
(2)根据图象直接写出????1????+????(3)求△????????????的面积.
?
(2)由图象得:当03时,????1????+????(3)∵直线????=?2????+8与????轴相交于点????,
∴????的坐标是(0,8).
∴????Δ????????????=????Δ?????????????????Δ????????????=12×8×(3?1)=8.
?
热考题型
考点三 反比例函数与一次函数综合
3.(2023·四川乐山·二模)如图,已知正比例函数????=2????与反比例函数????=????????????≠0的图象都经过点A和点B,点A的横坐标为1,过点A作x轴的垂线,垂足为M,连接????????.
(1)这个反比例函数的解析式;
(2)△????????????的面积.
?
【详解】(1)解:∵点A在正比例函数????=2????的图象上,
∴????=2×1=2,∴????1,2;
又∵点A在反比例函数????=????????????≠0的图象上,
∴2=????1,
解得:????=2,
∴反比例函数的解析式为????=2????;
?
热考题型
考点三 反比例函数与一次函数综合
3.(2023·四川乐山·二模)如图,已知正比例函数????=2????与反比例函数????=????????????≠0的图象都经过点A和点B,点A的横坐标为1,过点A作x轴的垂线,垂足为M,连接????????.
(1)这个反比例函数的解析式;
(2)△????????????的面积.
?
(2)解:∵????1,2,
∴????????=2,????????=1,
∴????△????????????=12×1×2=1,
∴????△????????????=2????△????????????=2.
?
热考题型
考点三 反比例函数与一次函数综合
4.(2023·西藏·模拟预测)如图,已知一次函数????=?????+????的图象与反比例函数????=????????的图象交于????4,?2,?????2,????两点.
(1)请直接写出不等式?????+????≤????????的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点????作????轴的垂线,垂足为????,连接????????,求△????????????的面积.
?
【详解】(1)解:由图象可知,不等式?????+????≤????????的解集为?2≤????<0或????≥4;
(2)解:∵一次函数????=?????+????的图象与反比例函数????=????????的图象交于????(4,?2)、????(?2,????)两点,
∴????=4×?2=?2????,?2=?4+????,
解得????=?8,????=4,????=2,
∴反比例函数和一次函数的解析式分别为????=?8????,????=?????+2;
(3)解:????△????????????=12×2×4+2=6.
?
热考题型
考点三 反比例函数与一次函数综合
5.(2024·内蒙古呼和浩特·模拟预测)如图,在平面直角坐标系中,一次函数????1=????????+????的图象与反比例函数????2=????????的图象交于点????1,????和?????2,?1.
(1)求一次函数和反比例函数的表达式;
(2)请直接写出????1(3)过点B作????????⊥????轴,????????⊥????????于点D,点C是直线????????上一点,若????????=2????????,求点C的坐标.
?
热考题型
考点三 反比例函数与一次函数综合
5.(2024·内蒙古呼和浩特·模拟预测)如图,在平面直角坐标系中,一次函数????1=????????+????的图象与反比例函数????2=????????的图象交于点????1,????和?????2,?1.
(1)求一次函数和反比例函数的表达式;
(2)请直接写出????1(3)过点B作????????⊥????轴,????????⊥????????于点D,点C是直线????????上一点,若????????=2????????,求点C的坐标.
?
(2)不等式????1(3)根据????1,2,?????2,?1,得到?????2,2,设?????2,????,
则????????=?2?12+?????22,????????=2?????,
∵????????=2????????, ∴9+???22=4?????22,
解得????1=2+3,????2=2?3,
故点C的坐标为(?2,2?3)或(?2,2+3).
?
考点剖析
考点四 反比例函数的实际应用
用反比例函数解决实际问题的步骤:
1)审:审清题意,找出题目中的常量、变量,并理清常量与变量之间的关系;
2)设:根据常量与变量之间的关系,设出函数解析式,待定的系数用字母表示;
3)列:由题目中的已知条件列出方程,求出待定系数;
4)写:写出函数解析式,并注意解析式中变量的取值范围;
5)解:用函数解析式去解决实际问题.
利用反比例函数解决实际问题,要做到:
1)能把实际的问题转化为数学问题,建立反比例函数的数学模型;
2)注意在自变量和函数值的取值上的实际意义;
3)问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.
【易错点】
1.利用反比例函数的性质时,误认为所给出的点在同一曲线上;
2.利用函数图象解决实际问题时,容易忽视自变量在实际问题的意义.
热考题型
考点四 反比例函数的实际应用
1.(23-24九年级上·山东济南·期中)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中????????段是恒温阶段,????????段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(1)求????????段反比例函数图象的关系式,并写出自变量x的取值范围;
(2)恒温阶段保持的时间有多少小时?
(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
?
【详解】(1)解:设????????对应函数解析式为????=????????(????≠0),
把????24,10代入????=????????(????≠0)中得:????=24×10=240,
∴????=240????,
当????=20时,20=240????,解得????=12,即????=12;
∴????=240????12?
热考题型
考点四 反比例函数的实际应用
1.(23-24九年级上·山东济南·期中)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中????????段是恒温阶段,????????段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(1)求????????段反比例函数图象的关系式,并写出自变量x的取值范围;
(2)恒温阶段保持的时间有多少小时?
(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
?
(2)解:由(1)知????=12,
∵ ????2,20,
∴恒温阶段保持的时间有:12?2=10(小时),
答:恒温阶段保持的时间有10小时;
?
热考题型
考点四 反比例函数的实际应用
1.(23-24九年级上·山东济南·期中)某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)与时间x(h)之间的函数关系如图所示,其中????????段是恒温阶段,????????段是某反比例函数图象的一部分,请根据图中信息解答下列问题:
(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长,若某天恒温系统开启前的温度是10℃,那么这种蔬菜一天内最适合生长的时间有多长?
?
热考题型
考点四 反比例函数的实际应用
2.(23-24八年级下·湖南衡阳·期中)我校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果????(单位:效力)与时间????(单位:分钟)呈现三段函数图象,其中????????段为渐消毒阶段,????????段为深消毒阶段,????????段是反比例函数图象的一部分,为降消毒阶段,请根据图中信息解答下列问题:
(1)第3分钟时消毒效果为________效力;
(2)求深消毒阶段和降消毒阶段中????与????之间的函数关系式;
(3)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
?
【详解】(1)解:由图象可知,第3分钟处于????????段渐消毒阶段,
设渐消毒阶段的函数解析式为????=????????,
将点10,3代入得:10????=3,解得:????=0.3,
∴渐消毒阶段的函数解析式为????=0.3????,
当????=3时,????=0.3×3=0.9,
即第3分钟时消毒效果为0.9效力,
故答案为:0.9
?
热考题型
考点四 反比例函数的实际应用
2.(23-24八年级下·湖南衡阳·期中)我校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果????(单位:效力)与时间????(单位:分钟)呈现三段函数图象,其中????????段为渐消毒阶段,????????段为深消毒阶段,????????段是反比例函数图象的一部分,为降消毒阶段,请根据图中信息解答下列问题:
(2)求深消毒阶段和降消毒阶段中????与????之间的函数关系式;
?
热考题型
考点四 反比例函数的实际应用
2.(23-24八年级下·湖南衡阳·期中)我校后勤处每周周日均会对学校教室进行消毒处理,已知消毒水的消毒效果随着时间变化如图所示,消毒效果????(单位:效力)与时间????(单位:分钟)呈现三段函数图象,其中????????段为渐消毒阶段,????????段为深消毒阶段,????????段是反比例函数图象的一部分,为降消毒阶段,请根据图中信息解答下列问题:
(3)若消毒效果持续28分钟达到4效力及以上,即可产生消毒作用,请问本次消毒是否有效?
?
(3)解:当深消毒阶段消毒效果达到4效力时,则0.15????+1.5=4,
解得:????=1623;
当降消毒阶段消毒效果达到4效力时,则4=180????,
解得:????=45,
∵45?1623=2813>28,
即本次消毒有效.
同课章节目录
