专题04 长方体的再认识(考点串讲)课件(共20张PPT)-六年级数学下学期期末考点大串讲(沪教版)
文档属性
| 名称 | 专题04 长方体的再认识(考点串讲)课件(共20张PPT)-六年级数学下学期期末考点大串讲(沪教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 610.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览






文档简介
六年级沪教版数学下册期末考点大串讲
串讲04 长方体的再认识
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
易错易混专练
6道期末真题对应考点练
五大重难点题型典例剖析+技巧总结
四大常考点:知识梳理
考点透视
1.长方体的元素
典例剖析
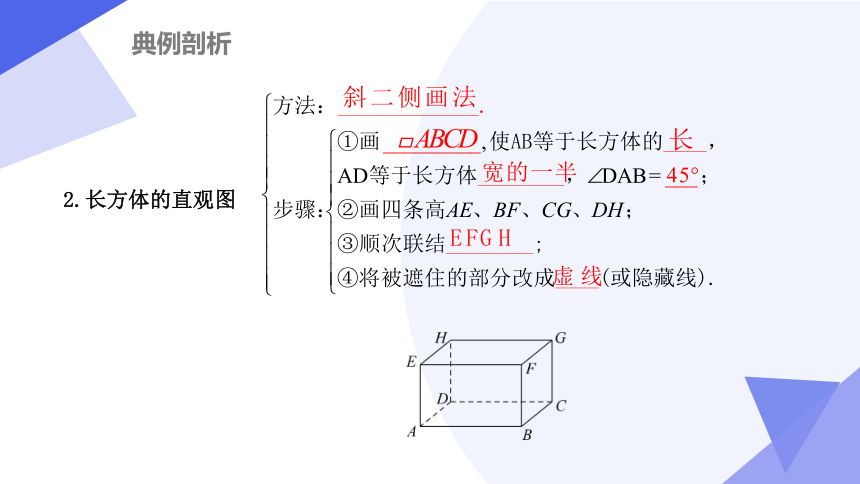
2.长方体的直观图
典例剖析
3.长方体中棱与棱的关系
4.长方体中棱与平面的关系
5.长方体中平面与平面的位置关系
1.某长方体的长、宽、高的长度之比为5:4:3,如果这个长方体所有棱长的和为48厘米,那么这个长方体的表面积是多少?
解 设长方体的长为5x厘米,宽4x厘米,宽为3x厘米.
解得 x = 1
所以长方体的长为5厘米,宽4厘米,宽为3厘米.
长方体的表面积公式:
答:这个长方体的表面积是94平方厘米.
题型剖析
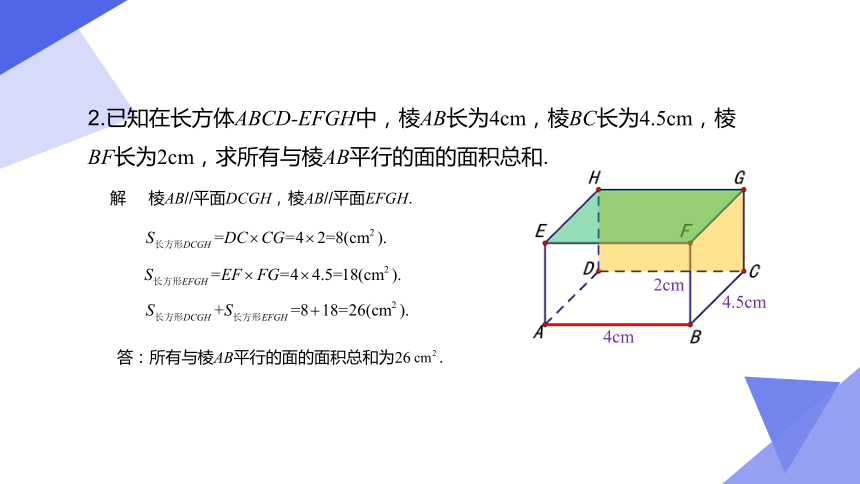
2.已知在长方体ABCD-EFGH中,棱AB长为4cm,棱BC长为4.5cm,棱BF长为2cm,求所有与棱AB平行的面的面积总和.
4cm
4.5cm
2cm
解 棱AB//平面DCGH,
棱AB//平面EFGH.
答:所有与棱AB平行的面的面积总和为26 .
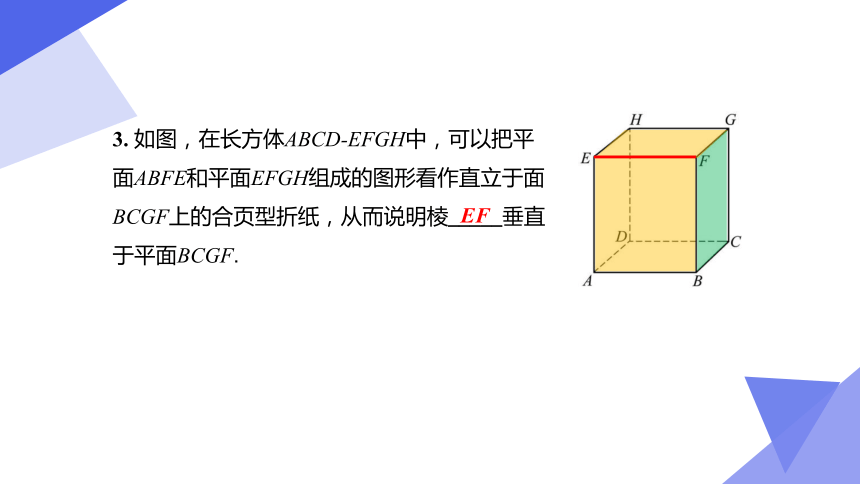
3. 如图,在长方体ABCD-EFGH中,可以把平面ABFE和平面EFGH组成的图形看作直立于面BCGF上的合页型折纸,从而说明棱_____垂直于平面BCGF.
EF
4.如图,在长方体ABCD-EFGH中,
(1)与棱DC异面的棱有______________________.
棱AE、
棱BF、
棱EH、
棱FG
(2)与棱AD平行的面有______________________.
平面EFGH、
平面BCGF
(3)与平面DCGH平行的面有_____________.
平面ABFE
5. 在如图所示的长方体ABCD-EFGH中,
(1)写出所有垂直于平面CDEF的平面.
平面ADHE、平面BCGF.
(2)写出既与平面CDHG垂直,又与平面ABCD垂直的平面.
与平面CDHG垂直的平面:
平面ADHE、平面BCGF、
平面EFGH、平面ABCD.
与平面ABCD垂直的平面:
平面ADHE、平面BCGF、平面DCGH、平面ABFE.
所以既与平面CDHG垂直又与平面ABCD垂直的平面:
平面ADHE、平面BCGF.
1.如图所示,与棱AB异面的棱有( ____ )
A.5条 B.4条 C.3条 D.2条
【解析】解:如图,与棱AB异面的棱有:A1D1,B1C1,DD1,CC1,共4条.
故选:B.
B
易错易混
2.如图,在长方体ABCD-EFGH中,可以把平面ABFE与平面EFGH组成的图形看作直立于面BCGF上的合页形折纸从而说明棱 ____ 垂直于平面BCGF.
【解析】解:把平面ABFE与平面EFGH组成的图形看作直立于面BCGF上的合页形折纸从而说明棱EF垂直于平面BCGF,
故答案为:EF.
EF
3.(1)补全下列图形,使之成为长方体ABCD-A1B1C1D1的直观图(不必写画法).
(2)结合图形,回答下列问题:
与棱AB垂直的平面有 ____ 个;这个长方体所有棱长和为36cm,如果长比高多1cm,宽比高少1cm,那么这个长方体的高是 ____ cm.
【解析】解:(1)根据已知条件补全图形,如图:
(2)与棱AB垂直的平面有2个;(面ADD1A1和面BCC1B1)
长+宽+高=36÷4=9(cm),
高:9÷3=3(cm),
故答案为:2;3.
2
3
4.现有一长宽高分别为50cm,40cm,30cm的长方体水槽中,原有9.1cm深的水,相继向其中放入一个棱长20cm的正方体铁块与一个棱长10cm的正方体铁块(并排放型,非叠放),求此时的水面高度为多少?
【解析】解:①假如水面高度不超过10cm,设此时水面高度为xcm,依题意列方程,50×40×(x-9.1)=20×20×x+10×10×x,
解得x≈12与题意不符,舍去.
②假如水面高度超过10cm而不超过20cm,设此时水面高度为xcm,依题意列方程,50×40×(x-9.1)=20×20×x+10×10×10,
解得x=12,符合题意.
答:此时水面高度为12cm.
1.(2023春?浦东新区期末)如图,长方体ABCD-EFGH中,线段EG与棱AD的位置关系是 __________ .
【解析】解:由图形可得:EG与AD为异面直线.
故答案为:异面直线.
异面直线
押题预测
2.(2023春?宝山区期末)如图,在长方体ABCD-EFGH中,与面ADHE平行的面是 _________ .
面BCGF
【解析】解:根据长方体的特征,相对的面的面积相等且平行,由此得:与面ADHE平行的面是面BCGF.
故答案为:面BCGF.
3.(2023春?松江区期末)如图,在长方体ABCD-EFGH中,可以把面DCGH与面BCGF组成的图形看作直立于面ABCD上的合页型折纸,从而说明棱 ____ ⊥面ABCD.
【解析】解:∵面DCGH与面BCGF组成的图形看作直立于面ABCD上的合页型折纸,
∴棱 CG⊥面ABCD,
故答案为:CG.
CG
4.(2022春?徐汇区校级期末)如图,把11块相同的小长方体砖块拼成了一个新的大长方体,已知大长方体的棱长总和是188cm,则每一块砖的体积是 _____ cm3.
【解析】答案:288.
解析:用a、b、h分别表示小长方体的长、宽、高,
显然,a=4h,即 ????=???????????? ,2a=3b即 ????=???????????? ,
根据大长方体的棱长总和可得方程: (????????+????+????????????+????????????)×????=???????????? ,
????????????????????×????=???????????? , ????????????????=????????????,a=12,
所以 ????=????????×????????=???? (厘米), ????=????????×????????=???? (厘米),
所以长方体的体积是:12×8×3=288(立方厘米),每块砖的体积是288立方厘米.
?
288
5.(2023春?松江区期末)如图,在长方体ABCD-EFGH中,与棱HD异面的棱是 _________________ .
【解析】解:由图可得,与棱HD异面的棱有:EF、AB、GF、BC,
故答案为:EF、AB、GF、BC.
EF、AB、GF、BC
6.(2023春?长宁区期末)用斜二测西法画长方体直观图:
(1)补全长方体ABCD-A1B1C1D1;
(2)若量得图中B1C1的长度是1cm,则所表示的实际长方体B1C1长度是 cm.
(3)与平面A1ABB1平行的平面是 .
【解析】解:(1)如图,长方体ABCD-A1B1C1D1即为所求.
____
(2)测量B1C1=1cm,AB=2cm,∴B1C1的实际长度为2cm.
故答案为:2.
(3)与平面A1ABB1平行的平面是面C1CDD1,
故答案为:面C1CDD1.
串讲04 长方体的再认识
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
易错易混专练
6道期末真题对应考点练
五大重难点题型典例剖析+技巧总结
四大常考点:知识梳理
考点透视
1.长方体的元素
典例剖析
2.长方体的直观图
典例剖析
3.长方体中棱与棱的关系
4.长方体中棱与平面的关系
5.长方体中平面与平面的位置关系
1.某长方体的长、宽、高的长度之比为5:4:3,如果这个长方体所有棱长的和为48厘米,那么这个长方体的表面积是多少?
解 设长方体的长为5x厘米,宽4x厘米,宽为3x厘米.
解得 x = 1
所以长方体的长为5厘米,宽4厘米,宽为3厘米.
长方体的表面积公式:
答:这个长方体的表面积是94平方厘米.
题型剖析
2.已知在长方体ABCD-EFGH中,棱AB长为4cm,棱BC长为4.5cm,棱BF长为2cm,求所有与棱AB平行的面的面积总和.
4cm
4.5cm
2cm
解 棱AB//平面DCGH,
棱AB//平面EFGH.
答:所有与棱AB平行的面的面积总和为26 .
3. 如图,在长方体ABCD-EFGH中,可以把平面ABFE和平面EFGH组成的图形看作直立于面BCGF上的合页型折纸,从而说明棱_____垂直于平面BCGF.
EF
4.如图,在长方体ABCD-EFGH中,
(1)与棱DC异面的棱有______________________.
棱AE、
棱BF、
棱EH、
棱FG
(2)与棱AD平行的面有______________________.
平面EFGH、
平面BCGF
(3)与平面DCGH平行的面有_____________.
平面ABFE
5. 在如图所示的长方体ABCD-EFGH中,
(1)写出所有垂直于平面CDEF的平面.
平面ADHE、平面BCGF.
(2)写出既与平面CDHG垂直,又与平面ABCD垂直的平面.
与平面CDHG垂直的平面:
平面ADHE、平面BCGF、
平面EFGH、平面ABCD.
与平面ABCD垂直的平面:
平面ADHE、平面BCGF、平面DCGH、平面ABFE.
所以既与平面CDHG垂直又与平面ABCD垂直的平面:
平面ADHE、平面BCGF.
1.如图所示,与棱AB异面的棱有( ____ )
A.5条 B.4条 C.3条 D.2条
【解析】解:如图,与棱AB异面的棱有:A1D1,B1C1,DD1,CC1,共4条.
故选:B.
B
易错易混
2.如图,在长方体ABCD-EFGH中,可以把平面ABFE与平面EFGH组成的图形看作直立于面BCGF上的合页形折纸从而说明棱 ____ 垂直于平面BCGF.
【解析】解:把平面ABFE与平面EFGH组成的图形看作直立于面BCGF上的合页形折纸从而说明棱EF垂直于平面BCGF,
故答案为:EF.
EF
3.(1)补全下列图形,使之成为长方体ABCD-A1B1C1D1的直观图(不必写画法).
(2)结合图形,回答下列问题:
与棱AB垂直的平面有 ____ 个;这个长方体所有棱长和为36cm,如果长比高多1cm,宽比高少1cm,那么这个长方体的高是 ____ cm.
【解析】解:(1)根据已知条件补全图形,如图:
(2)与棱AB垂直的平面有2个;(面ADD1A1和面BCC1B1)
长+宽+高=36÷4=9(cm),
高:9÷3=3(cm),
故答案为:2;3.
2
3
4.现有一长宽高分别为50cm,40cm,30cm的长方体水槽中,原有9.1cm深的水,相继向其中放入一个棱长20cm的正方体铁块与一个棱长10cm的正方体铁块(并排放型,非叠放),求此时的水面高度为多少?
【解析】解:①假如水面高度不超过10cm,设此时水面高度为xcm,依题意列方程,50×40×(x-9.1)=20×20×x+10×10×x,
解得x≈12与题意不符,舍去.
②假如水面高度超过10cm而不超过20cm,设此时水面高度为xcm,依题意列方程,50×40×(x-9.1)=20×20×x+10×10×10,
解得x=12,符合题意.
答:此时水面高度为12cm.
1.(2023春?浦东新区期末)如图,长方体ABCD-EFGH中,线段EG与棱AD的位置关系是 __________ .
【解析】解:由图形可得:EG与AD为异面直线.
故答案为:异面直线.
异面直线
押题预测
2.(2023春?宝山区期末)如图,在长方体ABCD-EFGH中,与面ADHE平行的面是 _________ .
面BCGF
【解析】解:根据长方体的特征,相对的面的面积相等且平行,由此得:与面ADHE平行的面是面BCGF.
故答案为:面BCGF.
3.(2023春?松江区期末)如图,在长方体ABCD-EFGH中,可以把面DCGH与面BCGF组成的图形看作直立于面ABCD上的合页型折纸,从而说明棱 ____ ⊥面ABCD.
【解析】解:∵面DCGH与面BCGF组成的图形看作直立于面ABCD上的合页型折纸,
∴棱 CG⊥面ABCD,
故答案为:CG.
CG
4.(2022春?徐汇区校级期末)如图,把11块相同的小长方体砖块拼成了一个新的大长方体,已知大长方体的棱长总和是188cm,则每一块砖的体积是 _____ cm3.
【解析】答案:288.
解析:用a、b、h分别表示小长方体的长、宽、高,
显然,a=4h,即 ????=???????????? ,2a=3b即 ????=???????????? ,
根据大长方体的棱长总和可得方程: (????????+????+????????????+????????????)×????=???????????? ,
????????????????????×????=???????????? , ????????????????=????????????,a=12,
所以 ????=????????×????????=???? (厘米), ????=????????×????????=???? (厘米),
所以长方体的体积是:12×8×3=288(立方厘米),每块砖的体积是288立方厘米.
?
288
5.(2023春?松江区期末)如图,在长方体ABCD-EFGH中,与棱HD异面的棱是 _________________ .
【解析】解:由图可得,与棱HD异面的棱有:EF、AB、GF、BC,
故答案为:EF、AB、GF、BC.
EF、AB、GF、BC
6.(2023春?长宁区期末)用斜二测西法画长方体直观图:
(1)补全长方体ABCD-A1B1C1D1;
(2)若量得图中B1C1的长度是1cm,则所表示的实际长方体B1C1长度是 cm.
(3)与平面A1ABB1平行的平面是 .
【解析】解:(1)如图,长方体ABCD-A1B1C1D1即为所求.
____
(2)测量B1C1=1cm,AB=2cm,∴B1C1的实际长度为2cm.
故答案为:2.
(3)与平面A1ABB1平行的平面是面C1CDD1,
故答案为:面C1CDD1.
同课章节目录
