第十章 概率 复习学案(含解析)高中数学人教A版(2019)必修 第二册
文档属性
| 名称 | 第十章 概率 复习学案(含解析)高中数学人教A版(2019)必修 第二册 |
|
|
| 格式 | DOCX | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 10:50:14 | ||
图片预览




文档简介
第十章 概率 复 习
构建《概率》知识网络.
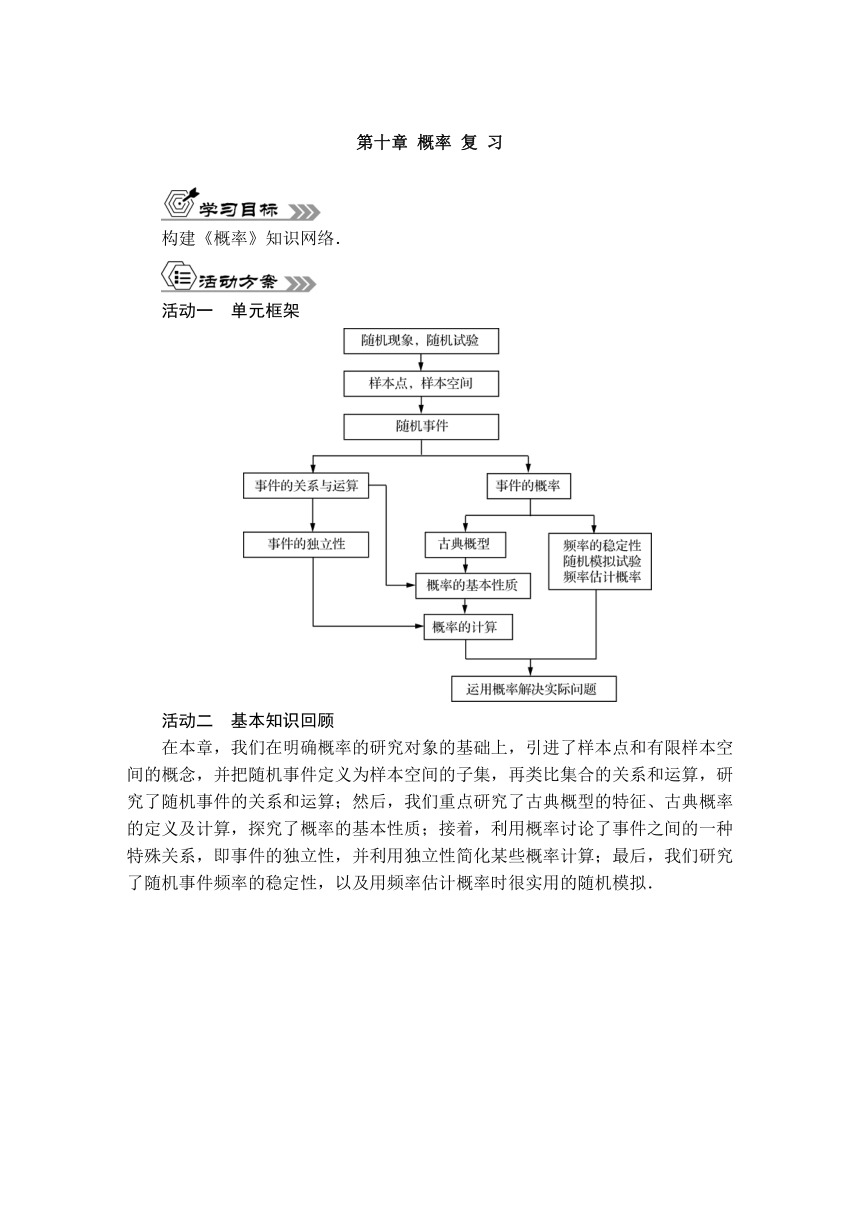
活动一 单元框架
活动二 基本知识回顾
在本章,我们在明确概率的研究对象的基础上,引进了样本点和有限样本空间的概念,并把随机事件定义为样本空间的子集,再类比集合的关系和运算,研究了随机事件的关系和运算;然后,我们重点研究了古典概型的特征、古典概率的定义及计算,探究了概率的基本性质;接着,利用概率讨论了事件之间的一种特殊关系,即事件的独立性,并利用独立性简化某些概率计算;最后,我们研究了随机事件频率的稳定性,以及用频率估计概率时很实用的随机模拟.
活动三 进一步掌握常见概率问题的求法
例1 从含有2件正品a1,a2 和1件次品b1 的3件产品中每次任取1件,每次取出后不放回,连续取两次.
(1) 求取出的2件产品中恰有1件次品的概率;
(2) 若将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的2件产品中恰有1件次品的概率是多少?
古典概型的问题,经常用枚举法列出样本空间,再找出所求事件的样本空间,最后根据概率公式计算即可.
有标号为1,2,3的3只小球及标号为1,2,3的3只盒子,现在随机地将3只小球放入3只盒子中,每盒一球,求球的编号与盒子的编号完全不同的概率.
例2 根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险的概率为0.3,设各车主至多购买一种保险.
(1) 求该地的1位车主购买甲、乙两种保险中的一种的概率;
(2) 求该地的1位车主甲、乙两种保险都不购买的概率.
若一个事件可以分解成若干个互斥事件,则根据互斥事件的概率公式计算即可;若一个事件的对立事件的概率比较方便解决,则先计算它的对立事件的概率,再用公式计算.
一个口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出2只球.求:
(1) 摸出的都是白球的概率;
(2) 摸出的至少有1只白球的概率.
例3 某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.求顾客抽奖1次能获奖的概率.
甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是,甲、丙两台机床加工的零件都是一等品的概率是.
(1) 分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2) 从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率.
1. (2023重庆模拟)对于一个古典概型的样本空间Ω和事件A,B,C,D,其中n(Ω)=60,n(A)=30,n(B)=10,n(C)=20,n(D)=30,n(A∪B)=40,n(A∩C)=10,n(A∪D)=60,则下列结论中正确的是( )
A. A与B不互斥 B. A与D互斥但不对立
C. C与D互斥 D. A与C相互独立
2. 某省新高考实行“3+1+2”模式,“3”为全国统考科目语文、数学、英语,所有学生必考;“1”为首选科目,考生需在物理、历史两科中选择一科;“2”为再选科目,考生可在化学、生物学、思想政治、地理4个科目中选择两科.某考生已经确定“首选科目”为物理,如果他从“再选科目”中随机选择两科,那么思想政治被选中的概率为( )
A. B. C. D.
3. (多选)黄种人群中各种血型的人所占的比例见下表:
血型 A B AB O
该血型的人所占比例 0.28 0.29 0.08 0.35
已知同种血型的人可以输血,O型血可以给任何一种血型的人输血,任何血型的人都可以给AB型血的人输血,其他不同血型的人不能互相输血,则下列结论中正确的是( )
A. 任找一个人,其血可以输给B型血的人的概率是0.64
B. 任找一个人,B型血的人能为其输血的概率是0.29
C. 任找一个人,其血可以输给O型血的人的概率为1
D. 任找一个人,其血可以输给AB型血的人的概率为1
4. 甲、乙两人下棋,甲不输的概率为,两人和棋的概率为,则甲获胜的概率为________.
5. 某中学根据学生的兴趣爱好,分别创建了“书法”“诗词”“理学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2023年某新生入学,已知他通过考核选拔进入该校的“书法”“诗词”“理学”三个社团的概率依次为m,,n,三个社团他都能进入的概率为,至少进入一个社团的概率为,且m>n.
(1) 求m与n的值;
(2) 该校根据三个社团活动的安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数不低于4分的概率.
【答案解析】
第十章 概率 复 习
【活动方案】
例1 (1) 每次取1件,取后不放回地连续取两次,其一切可能的结果组成的样本空间为Ω={(a1,a2),(a1,b1),(a2,a1),(a2,b1),(b1,a1),(b1,a2)},其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产品.Ω由6个基本事件组成,而且可以确定这些基本事件的出现是等可能的.
记事件A=“取出的2件中,恰好有1件次品”,则A={(a1,b1),(a2,b1),(b1,a1),(b1,a2)},事件A由4个基本事件组成,
所以P(A)==.
(2) 有放回地连续取出2件,其一切可能的结果组成的样本空间为Ω={(a1,a1),(a1,a2),(a1,b1),(a2,a1),(a2,a2),(a2,b1),(b1,a1),(b1,a2),(b1,b1)},由9个基本事件组成.由于每一件产品被取到的机会均等,因此可以确定这些基本事件的出现是等可能的.
记事件B=“取出的2件中,恰有1件次品”,则B={(a1,b1),(a2,b1),(b1,a1),(b1,a2)},事件B由4个基本事件组成,所以P(B)=.
跟踪训练 基本事件有6个,编号完全不同的事件有2个,所以P==.
例2 记事件A=“该地的1位车主购买甲种保险”;
事件B=“该地的1位车主购买乙种保险”;
事件C=“该地的1位车主购买甲、乙两种保险中的1种”;
事件D=“该地的1位车主甲、乙两种保险都不购买”.
(1) 由题意可知P(A)=0.5,P(B)=0.3,C=A∪B,
所以P(C)=P(A∪B)=P(A)+P(B)=0.8.
(2) D=,P(D)=1-P(C)=1-0.8=0.2.
跟踪训练 (1) 摸出2只球的基本事件有(白1,白2),(白1,白3),(白1,黑1),(白1,黑2),(白2,白3),(白2,黑1),(白2,黑2),(白3,黑1),(白3,黑2),(黑1,黑2),共10个,其中都是白球的事件有3个,所以P=.
(2) 至少摸出1只白球的事件有9个,故P=.
例3 记事件A1=“从甲箱中摸出的1个球是红球”,
A2=“从乙箱中摸出的1个球是红球”,
B1=“顾客抽奖1次获一等奖”,
B2=“顾客抽奖1次获二等奖”,
C=“顾客抽奖1次能获奖”.
由题意知A1与A2相互独立,A12与1A2互斥,B1与B2互斥,
且B1=A1A2,B2=(A12)∪(1A2),C=B1∪B2.
因为P(A1)==,P(A2)==,
所以P(B1)=P(A1A2)=P(A1)P(A2)=×=,
P(B2)=P(A12∪1A2)=P(A12)+P(1A2)
=P(A1)P(2)+P(1)P(A2)
=P(A1)(1-P(A2))+(1-P(A1))P(A2)
=×+×=,
故所求概率为P(C)=P(B1∪B2)=P(B1)+P(B2)=+=.
跟踪训练 (1)设A,B,C分别表示甲、乙、丙三台机床各自加工的零件是一等品的事件,那么
即
解得P(A)=,P(B)=,P(C)=,
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别为,,.
(2) 设事件D=“从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品”,则P(D)=1-P()=1-(1-P(A))(1-P(B))·(1-P(C))=1-××=,
即从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的概率是.
【检测反馈】
1. D 解析:由n(A)=30,n(B)=10,n(A∪B)=40,得n(A∪B)=n(A)+n(B),所以A与B互斥,故A错误;由n(A)=30,n(D)=30,n(A∪D)=60,n(Ω)=60,得n(A∪D)=n(A)+n(D)=n(Ω)=60,所以A与D互斥且对立,故B错误;又n(C)=20,n(A∩C)=10,则n(D∩C)=10,所以C与D不互斥,故C错误;由P(A)==,P(C)==,P(A∩C)==,得P(A∩C)=P(A)P(C),所以A与C相互独立,故D正确.
2. B 解析:化学、生物学、思想政治、地理4个科目中选择两科的情况有(化学,生物学),(化学,思想政治),(化学,地理),(生物学,思想政治),(生物学,地理),(思想政治,地理),共6种.两科中包括思想政治的情况有(化学,思想政治),(生物学,思想政治),(思想政治,地理),共3种,所以他从“再选科目”中随机选择两科,思想政治被选中的概率为.
3. AD 解析:任找一个人,其血型为A,B,AB,O型血的事件分别记为A′,B′,C′,D′,它们两两互斥.由已知,得P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.因为B,O型血可以输给B型血的人,所以“可以输给B型血的人”=B′∪D′,根据概率的加法公式,得P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64,故A正确;B型血的人能为B型、AB型的人输血,其概率为0.29+0.08=0.37,故B错误;由O型血只能接受O型血的人输血,知C错误;由任何人的血都可以输给AB型血的人,知D正确.故选AD.
4. 解析:设事件A=“甲不输”,B=“两人和棋”,C=“甲获胜”,则P(A)=,P(B)=,所以P(C)=P(A)-P(B)=.
5. (1) 由题意,得
解得
(2) 设该新同学在社团方面获得校本选修课学分的分数为i(i=0,1,2,3,4,5,6),
获得课本选修课学分分数不低于4分为事件A,
则P(i=4)=××=;
P(i=5)=××=;
P(i=6)=××=,
故P(A)=++=.
构建《概率》知识网络.
活动一 单元框架
活动二 基本知识回顾
在本章,我们在明确概率的研究对象的基础上,引进了样本点和有限样本空间的概念,并把随机事件定义为样本空间的子集,再类比集合的关系和运算,研究了随机事件的关系和运算;然后,我们重点研究了古典概型的特征、古典概率的定义及计算,探究了概率的基本性质;接着,利用概率讨论了事件之间的一种特殊关系,即事件的独立性,并利用独立性简化某些概率计算;最后,我们研究了随机事件频率的稳定性,以及用频率估计概率时很实用的随机模拟.
活动三 进一步掌握常见概率问题的求法
例1 从含有2件正品a1,a2 和1件次品b1 的3件产品中每次任取1件,每次取出后不放回,连续取两次.
(1) 求取出的2件产品中恰有1件次品的概率;
(2) 若将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的2件产品中恰有1件次品的概率是多少?
古典概型的问题,经常用枚举法列出样本空间,再找出所求事件的样本空间,最后根据概率公式计算即可.
有标号为1,2,3的3只小球及标号为1,2,3的3只盒子,现在随机地将3只小球放入3只盒子中,每盒一球,求球的编号与盒子的编号完全不同的概率.
例2 根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险的概率为0.3,设各车主至多购买一种保险.
(1) 求该地的1位车主购买甲、乙两种保险中的一种的概率;
(2) 求该地的1位车主甲、乙两种保险都不购买的概率.
若一个事件可以分解成若干个互斥事件,则根据互斥事件的概率公式计算即可;若一个事件的对立事件的概率比较方便解决,则先计算它的对立事件的概率,再用公式计算.
一个口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出2只球.求:
(1) 摸出的都是白球的概率;
(2) 摸出的至少有1只白球的概率.
例3 某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.求顾客抽奖1次能获奖的概率.
甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是,甲、丙两台机床加工的零件都是一等品的概率是.
(1) 分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2) 从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率.
1. (2023重庆模拟)对于一个古典概型的样本空间Ω和事件A,B,C,D,其中n(Ω)=60,n(A)=30,n(B)=10,n(C)=20,n(D)=30,n(A∪B)=40,n(A∩C)=10,n(A∪D)=60,则下列结论中正确的是( )
A. A与B不互斥 B. A与D互斥但不对立
C. C与D互斥 D. A与C相互独立
2. 某省新高考实行“3+1+2”模式,“3”为全国统考科目语文、数学、英语,所有学生必考;“1”为首选科目,考生需在物理、历史两科中选择一科;“2”为再选科目,考生可在化学、生物学、思想政治、地理4个科目中选择两科.某考生已经确定“首选科目”为物理,如果他从“再选科目”中随机选择两科,那么思想政治被选中的概率为( )
A. B. C. D.
3. (多选)黄种人群中各种血型的人所占的比例见下表:
血型 A B AB O
该血型的人所占比例 0.28 0.29 0.08 0.35
已知同种血型的人可以输血,O型血可以给任何一种血型的人输血,任何血型的人都可以给AB型血的人输血,其他不同血型的人不能互相输血,则下列结论中正确的是( )
A. 任找一个人,其血可以输给B型血的人的概率是0.64
B. 任找一个人,B型血的人能为其输血的概率是0.29
C. 任找一个人,其血可以输给O型血的人的概率为1
D. 任找一个人,其血可以输给AB型血的人的概率为1
4. 甲、乙两人下棋,甲不输的概率为,两人和棋的概率为,则甲获胜的概率为________.
5. 某中学根据学生的兴趣爱好,分别创建了“书法”“诗词”“理学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2023年某新生入学,已知他通过考核选拔进入该校的“书法”“诗词”“理学”三个社团的概率依次为m,,n,三个社团他都能进入的概率为,至少进入一个社团的概率为,且m>n.
(1) 求m与n的值;
(2) 该校根据三个社团活动的安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数不低于4分的概率.
【答案解析】
第十章 概率 复 习
【活动方案】
例1 (1) 每次取1件,取后不放回地连续取两次,其一切可能的结果组成的样本空间为Ω={(a1,a2),(a1,b1),(a2,a1),(a2,b1),(b1,a1),(b1,a2)},其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产品.Ω由6个基本事件组成,而且可以确定这些基本事件的出现是等可能的.
记事件A=“取出的2件中,恰好有1件次品”,则A={(a1,b1),(a2,b1),(b1,a1),(b1,a2)},事件A由4个基本事件组成,
所以P(A)==.
(2) 有放回地连续取出2件,其一切可能的结果组成的样本空间为Ω={(a1,a1),(a1,a2),(a1,b1),(a2,a1),(a2,a2),(a2,b1),(b1,a1),(b1,a2),(b1,b1)},由9个基本事件组成.由于每一件产品被取到的机会均等,因此可以确定这些基本事件的出现是等可能的.
记事件B=“取出的2件中,恰有1件次品”,则B={(a1,b1),(a2,b1),(b1,a1),(b1,a2)},事件B由4个基本事件组成,所以P(B)=.
跟踪训练 基本事件有6个,编号完全不同的事件有2个,所以P==.
例2 记事件A=“该地的1位车主购买甲种保险”;
事件B=“该地的1位车主购买乙种保险”;
事件C=“该地的1位车主购买甲、乙两种保险中的1种”;
事件D=“该地的1位车主甲、乙两种保险都不购买”.
(1) 由题意可知P(A)=0.5,P(B)=0.3,C=A∪B,
所以P(C)=P(A∪B)=P(A)+P(B)=0.8.
(2) D=,P(D)=1-P(C)=1-0.8=0.2.
跟踪训练 (1) 摸出2只球的基本事件有(白1,白2),(白1,白3),(白1,黑1),(白1,黑2),(白2,白3),(白2,黑1),(白2,黑2),(白3,黑1),(白3,黑2),(黑1,黑2),共10个,其中都是白球的事件有3个,所以P=.
(2) 至少摸出1只白球的事件有9个,故P=.
例3 记事件A1=“从甲箱中摸出的1个球是红球”,
A2=“从乙箱中摸出的1个球是红球”,
B1=“顾客抽奖1次获一等奖”,
B2=“顾客抽奖1次获二等奖”,
C=“顾客抽奖1次能获奖”.
由题意知A1与A2相互独立,A12与1A2互斥,B1与B2互斥,
且B1=A1A2,B2=(A12)∪(1A2),C=B1∪B2.
因为P(A1)==,P(A2)==,
所以P(B1)=P(A1A2)=P(A1)P(A2)=×=,
P(B2)=P(A12∪1A2)=P(A12)+P(1A2)
=P(A1)P(2)+P(1)P(A2)
=P(A1)(1-P(A2))+(1-P(A1))P(A2)
=×+×=,
故所求概率为P(C)=P(B1∪B2)=P(B1)+P(B2)=+=.
跟踪训练 (1)设A,B,C分别表示甲、乙、丙三台机床各自加工的零件是一等品的事件,那么
即
解得P(A)=,P(B)=,P(C)=,
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别为,,.
(2) 设事件D=“从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品”,则P(D)=1-P()=1-(1-P(A))(1-P(B))·(1-P(C))=1-××=,
即从甲、乙、丙三台机床加工的零件中各取一个检验,至少有一个一等品的概率是.
【检测反馈】
1. D 解析:由n(A)=30,n(B)=10,n(A∪B)=40,得n(A∪B)=n(A)+n(B),所以A与B互斥,故A错误;由n(A)=30,n(D)=30,n(A∪D)=60,n(Ω)=60,得n(A∪D)=n(A)+n(D)=n(Ω)=60,所以A与D互斥且对立,故B错误;又n(C)=20,n(A∩C)=10,则n(D∩C)=10,所以C与D不互斥,故C错误;由P(A)==,P(C)==,P(A∩C)==,得P(A∩C)=P(A)P(C),所以A与C相互独立,故D正确.
2. B 解析:化学、生物学、思想政治、地理4个科目中选择两科的情况有(化学,生物学),(化学,思想政治),(化学,地理),(生物学,思想政治),(生物学,地理),(思想政治,地理),共6种.两科中包括思想政治的情况有(化学,思想政治),(生物学,思想政治),(思想政治,地理),共3种,所以他从“再选科目”中随机选择两科,思想政治被选中的概率为.
3. AD 解析:任找一个人,其血型为A,B,AB,O型血的事件分别记为A′,B′,C′,D′,它们两两互斥.由已知,得P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.因为B,O型血可以输给B型血的人,所以“可以输给B型血的人”=B′∪D′,根据概率的加法公式,得P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64,故A正确;B型血的人能为B型、AB型的人输血,其概率为0.29+0.08=0.37,故B错误;由O型血只能接受O型血的人输血,知C错误;由任何人的血都可以输给AB型血的人,知D正确.故选AD.
4. 解析:设事件A=“甲不输”,B=“两人和棋”,C=“甲获胜”,则P(A)=,P(B)=,所以P(C)=P(A)-P(B)=.
5. (1) 由题意,得
解得
(2) 设该新同学在社团方面获得校本选修课学分的分数为i(i=0,1,2,3,4,5,6),
获得课本选修课学分分数不低于4分为事件A,
则P(i=4)=××=;
P(i=5)=××=;
P(i=6)=××=,
故P(A)=++=.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
