图形与几何-人教版数学五年级下册期末专项复习(含答案)
文档属性
| 名称 | 图形与几何-人教版数学五年级下册期末专项复习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 20:46:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
图形与几何
一、选择题
1.一个立体图形,从正面看到的形状是,从左面看到的形状是,下面( )符合条件。
A. B. C. D.
2.用5个同样的小正方体搭成一个几何体,从前面和上面看都是,这个几何体可能是( )。
A. B. C. D.
3.旋转过程中图案的变化规律是( )。
A.大小改变、位置不变 B.大小不变、位置改变
C.大小和位置都改变 D.大小和位置都不变
4.下列现象中,不属于旋转变换的是( )。
A.钟摆的运动 B.拧紧螺丝 C.电梯的升降运动 D.方向盘的转动
5.一个由同样大小的小正方体摆成的几何体,从正面看是,从左面看是,这个几何体至少要用( )个小正方体摆成,至多要用( )个小正方体摆成。
A.5;10 B.7;10 C.5;12 D.7;12
6.如下图,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片排序正确的是( )。
A.①②③④ B.①③②④ C.③②④① D.③①④②
二、填空题
7.小方和小丽一样高,可在同一路灯下,小方的影子比小丽的影子长,这是因为( )离路灯远,( )离路灯近。【来源:21·世纪·教育·网】
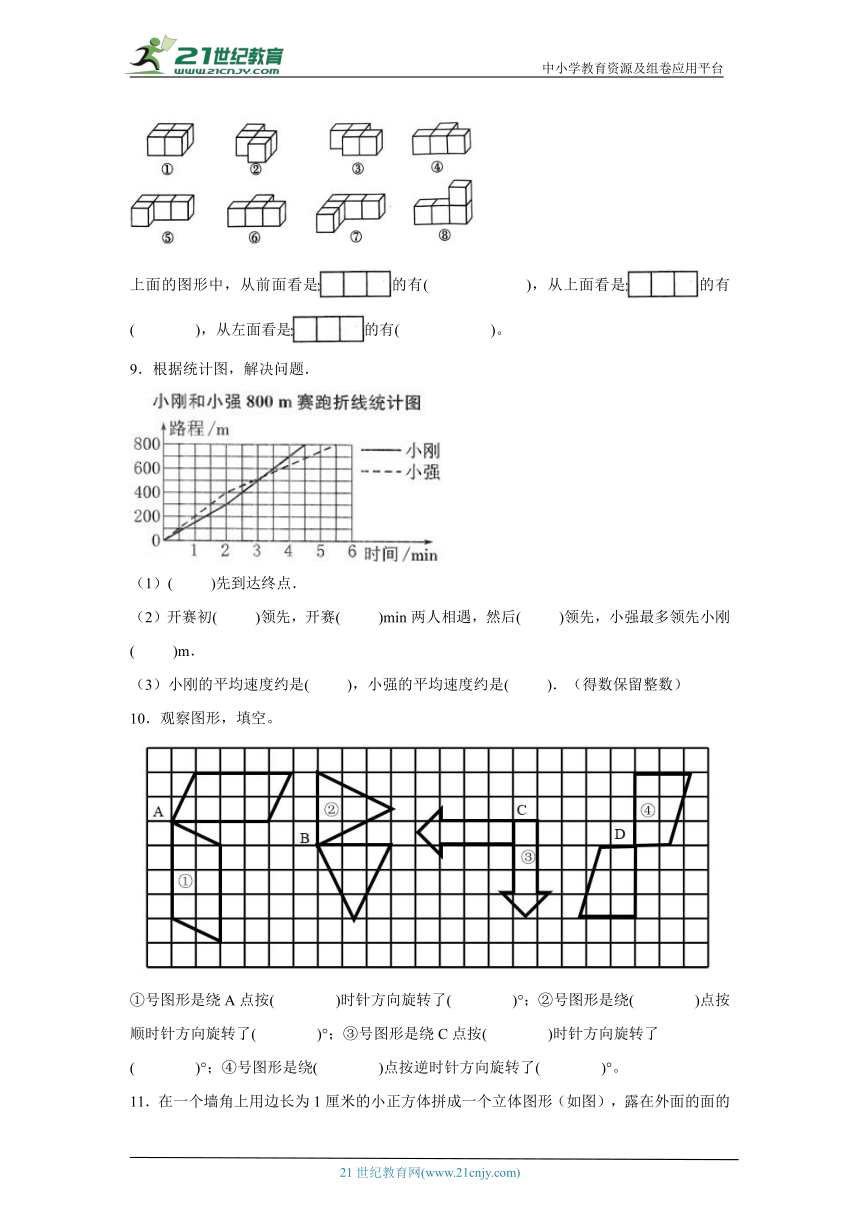
8.看图回答问题。(填序号)
上面的图形中,从前面看是的有( ),从上面看是的有( ),从左面看是的有( )。www-2-1-cnjy-com
9.根据统计图,解决问题.
(1)( )先到达终点.
(2)开赛初( )领先,开赛( )min两人相遇,然后( )领先,小强最多领先小刚( )m.【出处:21教育名师】
(3)小刚的平均速度约是( ),小强的平均速度约是( ).(得数保留整数)
10.观察图形,填空。
①号图形是绕A点按( )时针方向旋转了( )°;②号图形是绕( )点按顺时针方向旋转了( )°;③号图形是绕C点按( )时针方向旋转了( )°;④号图形是绕( )点按逆时针方向旋转了( )°。
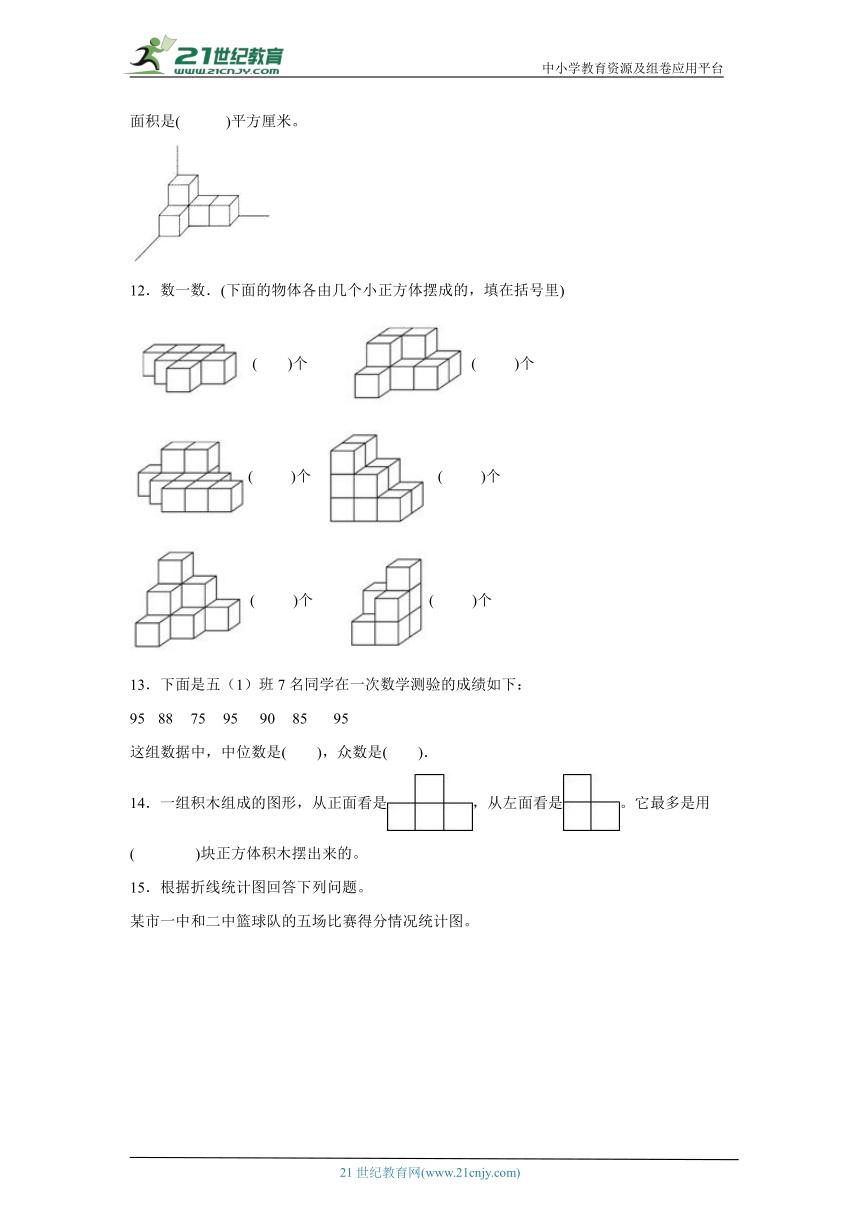
11.在一个墙角上用边长为1厘米的小正方体拼成一个立体图形(如图),露在外面的面的面积是( )平方厘米。2-1-c-n-j-y
12.数一数.(下面的物体各由几个小正方体摆成的,填在括号里)
( )个 ( )个
( )个 ( )个
( )个 ( )个
13.下面是五(1)班7名同学在一次数学测验的成绩如下:
95 88 75 95 90 85 95
这组数据中,中位数是( ),众数是( ).
14.一组积木组成的图形,从正面看是,从左面看是。它最多是用( )块正方体积木摆出来的。21教育名师原创作品
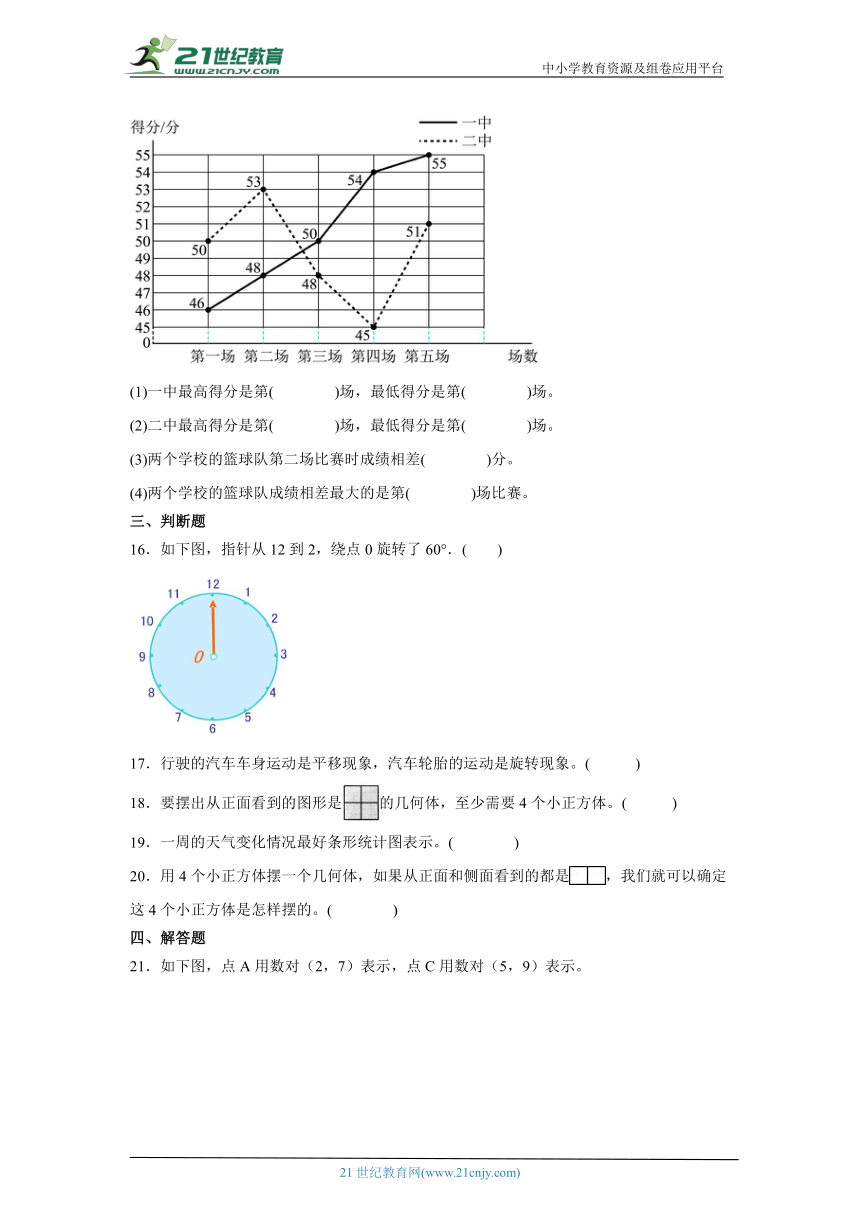
15.根据折线统计图回答下列问题。
某市一中和二中篮球队的五场比赛得分情况统计图。
(1)一中最高得分是第( )场,最低得分是第( )场。
(2)二中最高得分是第( )场,最低得分是第( )场。
(3)两个学校的篮球队第二场比赛时成绩相差( )分。
(4)两个学校的篮球队成绩相差最大的是第( )场比赛。
三、判断题
16.如下图,指针从12到2,绕点0旋转了60°.( )
17.行驶的汽车车身运动是平移现象,汽车轮胎的运动是旋转现象。( )
18.要摆出从正面看到的图形是的几何体,至少需要4个小正方体。( )
19.一周的天气变化情况最好条形统计图表示。( )
20.用4个小正方体摆一个几何体,如果从正面和侧面看到的都是,我们就可以确定这4个小正方体是怎样摆的。( )www.21-cn-jy.com
四、解答题
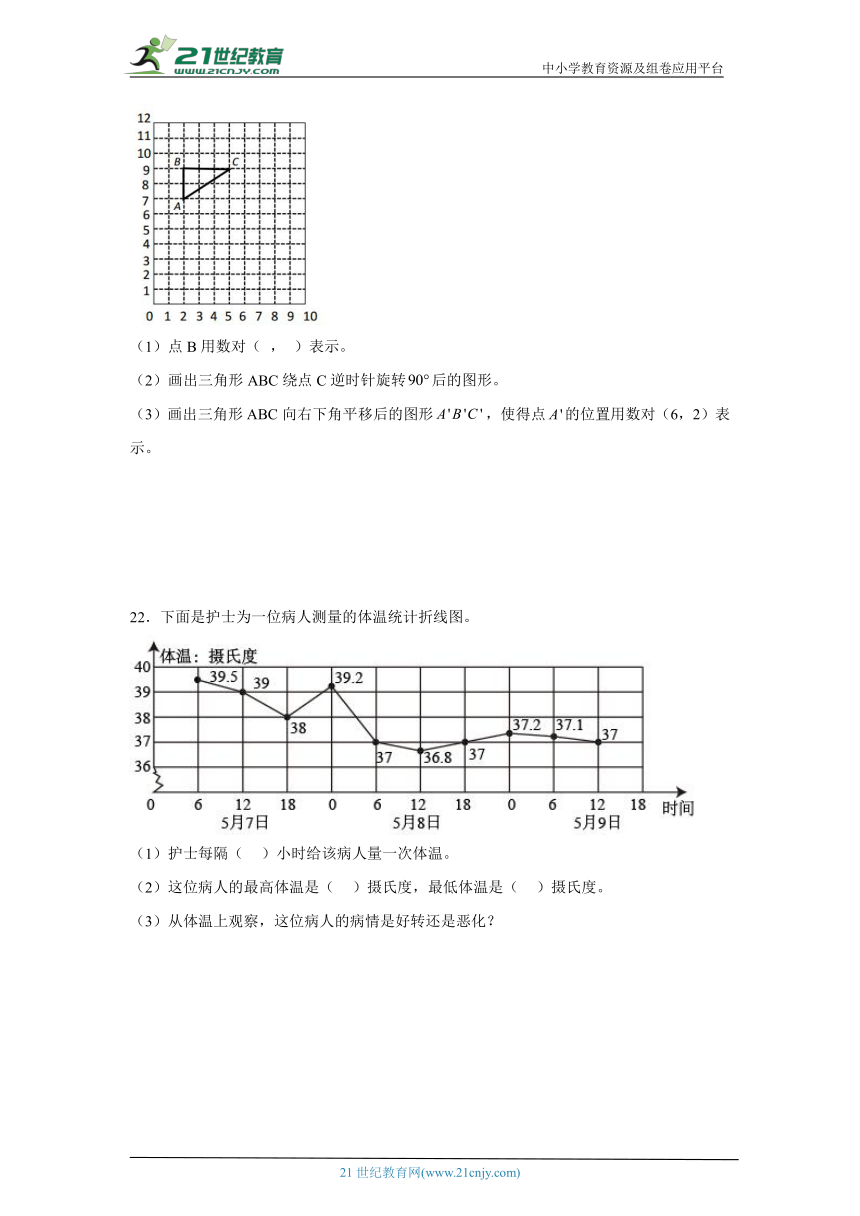
21.如下图,点A用数对(2,7)表示,点C用数对(5,9)表示。
(1)点B用数对( , )表示。
(2)画出三角形ABC绕点C逆时针旋转后的图形。
(3)画出三角形ABC向右下角平移后的图形,使得点的位置用数对(6,2)表示。
22.下面是护士为一位病人测量的体温统计折线图。
(1)护士每隔( )小时给该病人量一次体温。
(2)这位病人的最高体温是( )摄氏度,最低体温是( )摄氏度。
(3)从体温上观察,这位病人的病情是好转还是恶化?
23.在下图中,从图形A到图形B是怎样运动的 请你准确表述一下.
24.下面是某旅游景区去年接待游客情况统计图。
(1)去年两次旅游高峰,一次是( )月,另一次是( )月,这两个月的游客一共是( )万人。21cnjy.com
(2)去年游客人数最多的月份与最少的月份相差( )万人。
(3)去年游客月平均人数是( )万人。
(4)去年游客人数多于月平均人数的月份有( )个,少于月平均人数的月份有( )个。
(5)从这张统计图你还知道哪些信息?
25.下面表格中是李子轩和赵璐瑶五个月用于体育锻炼的月支出费用情况,请根据表中数据绘制出复式折线统计图。21·世纪*教育网
(1)从图中看,( )的体育锻炼月支出费用呈上升趋势。
(2)赵璐瑶这五个月用于体育锻炼的平均支出费用是( )元。
参考答案:
1.B
【分析】A.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
B.从正面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;21教育网
C.从正面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;2·1·c·n·j·y
D.从正面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【详解】A.从正面看到的形状是,从左面看到的形状是;
B.从正面看到的形状是,从左面看到的形状是;
C.从正面看到的形状是,从左面看到的形状是;
D.从正面看到的形状是,从左面看到的形状是。
故答案为:B
2.B
【分析】从上面看到的是,说明这个几何体的最下层是;从前面看到的是,说明这个几何体可能是、、;又因为这个几何体是由5个同样的小正方体搭成,所以这个几何体可能是或。再与四个选项进行对照可知,B选项是。
【详解】A.从前面看到的是,从上面看到的是。A选项错误。
B.从前面和上面看都是。B选项正确。
C.从前面看到的是,从上面看到的是。C选项错误。
D.从前面看到的是,从上面看到的是。D选项错误。
故答案为:B
【点睛】不同形状的几何体,从同一角度观察,得到的平面图形可能是相同的。
3.B
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
【详解】根据分析可知,旋转过程中图案的变化规律是形状、大小都不改变,只是位置发生了变化。
故答案为:B
【点睛】正确理解旋转的意义与特征,是解答此题的关键。
4.C
【分析】物体的旋转有两个特点: 一个旋转中心,物体的形状不变。逐项分析是否具备这两个条件,即可选择。
【详解】A.钟摆形状不变,围绕一个中心左右摆动,属于旋转。
B.拧紧螺丝,螺丝形状不变,围绕螺母转动,属于旋转。
C.电梯的升降运动,没有旋转中心,虽然形状不变,但不属于旋转。
D.方向盘的转动,也是形状不变,有旋转中心,属于旋转。
故答案为:C
【点睛】本题考查旋转的定义,熟记旋转的定义是关键。
5.B
【分析】从正面看有5个小正方体,从左面看有4个正方体,则至少需要7个小正方体摆成;至多有两排第一排有5个小正方体,第二排有5个小正方体,据此解答即可。
【详解】5+5=10(个)
所以这个几何体至少要用7个小正方体摆成,至多要用10个小正方体摆成。
故答案为:B
【点睛】本题考查通过三视图确定几何体,明确从不同方向观察到的正方体的个数是解题的关键。
6.C
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。小猴子在A点时,看到房子的图片是,从A点绕房子逆时针转90°时,这时看到房子的图片是,从A点绕房子逆时针转180°时,这时看到房子的图片是,从A点绕房子逆时针转270°时,这时看到房子的图片是;据此解答。
【详解】根据分析得,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片依次为:
。
故答案为:C
【点睛】此题主要考查旋转及旋转现象,明确旋转的定义是解题的关键。
7. 小方 小丽
【分析】因为光是沿直线传播的,以光源为端点,过物体的边沿画射线,射线内的部分就是物体的影子,物体越靠近光源,射线所形成的角度发生变化,影子会越来越短;反之就越来越长。据此解答。21*cnjy*com
【详解】根据分析得,小方的影子比小丽的影子长,说明小方离路灯的位置远,小丽离路灯的位置近。
【点睛】本题考查了从不同方向观察物体和几何体,需要注意人的影子的长短与人遮挡光的面积的大小有关。
8. ③④⑤⑥⑦ ⑧ ②⑦
【分析】
从前面看是,说明这个几何体只有一层,排除⑧,在剩下的几何体中找出从前面能看到3个小正方形的即可。
从上面看是,说明这个几何体只有一行,只有⑧符合要求;
从左面看是,说明这个几何体有一层三行,只有②⑦符合要求。
【详解】
上面的图形中,从前面看是的有③④⑤⑥⑦,从上面看是的有⑧,从左面看是的有②⑦。
9. 小刚 小强 3 小刚 100 178m/min 145m/min
【详解】略
10. 逆 90 B 90 顺 90 D 180
【分析】根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数,某点的位置不动,其余各部分均绕某点按相同的方向旋转相同的度数。据此解答。【版权所有:21教育】
【详解】①号图形是绕A点按逆时针方向旋转了90°;
②号图形是绕B点按顺时针方向旋转了90°;
③号图形是绕C点按顺时针方向旋转了90°;
④号图形是绕D点按逆时针方向旋转了180°。
【点睛】本题考查了图形的旋转,注意旋转三要素:旋转中心、旋转方向、旋转角。
11.11
【分析】计算出一个正方形面的面积,再数出一共有多少个露在外面的面,代入数据用乘法计算即可。
【详解】1×1×11
=1×11
=11(平方厘米)
【点睛】掌握正方形的面积计算公式,并准确数出露在外面的面,这是解决此题的关键。
12. 7 10 11 12 10 8
【详解】略
13. 90 95
【分析】将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.众数是一组数据中出现次数最多的数;据此解答即可.【来源:21cnj*y.co*m】
【详解】将这组数据从小到大排列为:75、85、88、90、95、95、95;所以中位数是90;众数是95.
故答案为90;95.
14.7
【分析】从正面看有2层,下边1层3个小正方形,上边1层中间1个小正方形;从左面看有2层,下边1层2个小正方形,上边靠左1个小正方形,再考虑遮挡,画出示意图,数一数即可。
【详解】从正面看是,从左面看是,最多如图,用7块正方体积木摆出来的。
【点睛】关键是具有一定的空间想象能力,可以画一画示意图。
15.(1) 五 一
(2) 二 四
(3)5
(4)四
【分析】(1)一中的折线是实线,通过观察统计图可知,一中最高得分和最低得分的场次。
(2)二中的折线是虚线,通过观察统计图可知,二中最高得分和最低得分的场次。
(3)从统计图中找到第二场比赛时两队的成绩,用减法计算即可。
(4)求出每场比赛成绩的差值,进行比较,得出两队成绩相差最大的场次。
【详解】(1)55>54>50>48>46
一中最高得分是第五场,最低得分是第一场。
(2)53>51>50>48>45
二中最高得分是第二场,最低得分是第四场。
(3)53-48=5(分)
两个学校的篮球队第二场比赛时成绩相差5分。
(4)第一场成绩相差:50-46=4(分)
第二场成绩相差:53-48=5(分)
第三场成绩相差:50-48=2(分)
第四场成绩相差:54-45=9(分)
第五场成绩相差:55-51=4(分)
9>5>4>2
所以两个学校的篮球队成绩相差最大的是第四场比赛。
【点睛】理解掌握复式折线统计图的特点,从统计图中获取信息,并且能够根据统计图提供的信息解决有关的实际问题。21·cn·jy·com
16.√
【分析】钟表上的时针从12走到2,是按顺时针走的,因为一个圆可以看成一个周角,一共是360°,1小时是60分钟,每个小格是1分钟,对应的角度就是360÷60=6°.
【详解】从12走到2,一共走了10个小格,也就是旋转了60°.
17.√
【分析】平移是把一个物体整体沿着某一个方向移动一定的距离;旋转是将一个物体绕一点按某个方向转动一个角度;根据平移与旋转定义判断即可。
【详解】行驶的汽车车身运动是平移现象,汽车轮胎的运动是旋转现象,说法正确。
故答案为:√
【点睛】本题考查了学生对于平移和旋转的理解以及在实际生活中的应用。
18.√
【分析】该几何体从正面看到的图形是,说明该几何体至少有一行,这一行里有两层,两层都是2个小正方体;所以至少是需要4个小正方体;据此解答。
【详解】由分析可知:要摆出从正面看到的图形是的几何体,至少需要4个小正方体,所以原题说法正确。
故答案为:√
【点睛】本题考查了观察物体,关键是要掌握从不同角度观察到的立体图形的特点,分析出该立体图形的形状。
19.×
【分析】条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
【详解】一周的天气变化情况最好折线统计图表示,所以原题说法错误。
故答案为:×
【点睛】关键是熟悉条形统计图和折线统计图的特点,根据统计图的特点确定统计图。
20.√
【分析】用4个小正方体摆一个几何体,如果从正面和侧面看到的都是,则这个几何体摆了1层,占地面积是个正方形,即前边1行2个小正方体,后边1行2个小正方体,据此分析。
【详解】根据分析,摆出来的几何体如图,是可以确定这4个小正方体是怎样摆的。
故答案为:√
【点睛】关键是具有一定的空间想象能力,可以画一画示意图帮助理解。
21.(1)(2,9)
(2)(3)
【分析】(1)表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点
【详解】(1)点B用数对(2,9)表示。
(2)(3)
【点睛】本题考查了数对与位置,作旋转和平移后的图形,平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
22.(1)6;(2)39.5;36.8;(3)好转
【分析】(1)求出横坐标每日一格表示的时间即可;
(2)找出最高点和最低点的纵坐标即可。
(3)观察统计图,结合正常体温解答即可。
【详解】(1)护士每隔6小时给该病人量一次体温。
(2)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度。
(3)人体的正常体温是37℃,病人后来的体温稳定在这一水平线上,说明病情好转。
【点睛】此题考查了折线统计图的实际应用,能够根据问题从统计图中提取有效数学信息是解题关键。
23.图形A先绕点O逆时针旋转90度,再向右平移10格得到图形B.(图形A先向右平移10格,再绕点O'逆时针旋转90度得到图形B.)21世纪教育网版权所有
【详解】略
24.(1)4;10;19;
(2)8;
(3)5;
(4)3;6;
(5)1月到4月旅游景区去年接待游客数量呈上升趋势;4月到6月以及10月到12月旅游景区去年接待游客数量呈下降趋势。
【分析】(1)由折线统计图可知,折线的最高点一个是4月份9万人,一个是10月份10万人;
(2)由折线统计图可知,游客人数最多的是10月份10万人,游客人数最少是1月份2万人;
(3)用这组数据的和除以数据的个数,就是平均数;
(4)计算折线统计图中游客人数多于5万人的月份和少于5万人的月份各有多少个;
(5)折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况,根据折线的走势分析人数的增减变化情况即可。
【详解】(1)9+10=19(万人)
去年两次旅游高峰,一次是4月,另一次是10月,这两个月的游客一共是19万人。
(2)10-2=8(万人)
去年游客人数最多的月份与最少的月份相差8万人。
(3)(2+3+5+9+6+4+4+5+5+10+4+3)÷12
=60÷12
=5(万人)
(4)去年游客人数多于月平均人数的月份有:4月、5月、10月,一共3个;
去年游客人数少于月平均人数的月份有:1月、2月、6月、7月、11月、12月,一共6个。
(5)由折线统计图可知,1月到4月旅游景区去年接待游客数量呈上升趋势;4月到6月以及10月到12月旅游景区去年接待游客数量呈下降趋势。(答案不唯一)
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
25.图见详解
(1)赵璐瑶(2)74
【分析】填补复式折线统计图:根据统计表中的数据描点,在描的点旁边注上数据,李子轩支出用实线连线,赵璐瑶支出数用虚线连线;21*cnjy*com
(1)观察统计图可得:李子轩后四个月用于体育锻炼月支出费用呈下降趋势,赵璐瑶的体育锻炼月支出费用呈上升趋势;
(2)根据“平均数=总数÷份数”,求出赵璐瑶这五个月用于体育锻炼的平均支出费用。
【详解】作图如下:
(1)从图中看,赵璐瑶的体育锻炼月支出费用呈上升趋势;
(2)(60+70+80+75+85)÷5
=370÷5
=74(元)
【点睛】读取统计表中的数据,填补复式折线统计图,根据统计图信息解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
图形与几何
一、选择题
1.一个立体图形,从正面看到的形状是,从左面看到的形状是,下面( )符合条件。
A. B. C. D.
2.用5个同样的小正方体搭成一个几何体,从前面和上面看都是,这个几何体可能是( )。
A. B. C. D.
3.旋转过程中图案的变化规律是( )。
A.大小改变、位置不变 B.大小不变、位置改变
C.大小和位置都改变 D.大小和位置都不变
4.下列现象中,不属于旋转变换的是( )。
A.钟摆的运动 B.拧紧螺丝 C.电梯的升降运动 D.方向盘的转动
5.一个由同样大小的小正方体摆成的几何体,从正面看是,从左面看是,这个几何体至少要用( )个小正方体摆成,至多要用( )个小正方体摆成。
A.5;10 B.7;10 C.5;12 D.7;12
6.如下图,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片排序正确的是( )。
A.①②③④ B.①③②④ C.③②④① D.③①④②
二、填空题
7.小方和小丽一样高,可在同一路灯下,小方的影子比小丽的影子长,这是因为( )离路灯远,( )离路灯近。【来源:21·世纪·教育·网】
8.看图回答问题。(填序号)
上面的图形中,从前面看是的有( ),从上面看是的有( ),从左面看是的有( )。www-2-1-cnjy-com
9.根据统计图,解决问题.
(1)( )先到达终点.
(2)开赛初( )领先,开赛( )min两人相遇,然后( )领先,小强最多领先小刚( )m.【出处:21教育名师】
(3)小刚的平均速度约是( ),小强的平均速度约是( ).(得数保留整数)
10.观察图形,填空。
①号图形是绕A点按( )时针方向旋转了( )°;②号图形是绕( )点按顺时针方向旋转了( )°;③号图形是绕C点按( )时针方向旋转了( )°;④号图形是绕( )点按逆时针方向旋转了( )°。
11.在一个墙角上用边长为1厘米的小正方体拼成一个立体图形(如图),露在外面的面的面积是( )平方厘米。2-1-c-n-j-y
12.数一数.(下面的物体各由几个小正方体摆成的,填在括号里)
( )个 ( )个
( )个 ( )个
( )个 ( )个
13.下面是五(1)班7名同学在一次数学测验的成绩如下:
95 88 75 95 90 85 95
这组数据中,中位数是( ),众数是( ).
14.一组积木组成的图形,从正面看是,从左面看是。它最多是用( )块正方体积木摆出来的。21教育名师原创作品
15.根据折线统计图回答下列问题。
某市一中和二中篮球队的五场比赛得分情况统计图。
(1)一中最高得分是第( )场,最低得分是第( )场。
(2)二中最高得分是第( )场,最低得分是第( )场。
(3)两个学校的篮球队第二场比赛时成绩相差( )分。
(4)两个学校的篮球队成绩相差最大的是第( )场比赛。
三、判断题
16.如下图,指针从12到2,绕点0旋转了60°.( )
17.行驶的汽车车身运动是平移现象,汽车轮胎的运动是旋转现象。( )
18.要摆出从正面看到的图形是的几何体,至少需要4个小正方体。( )
19.一周的天气变化情况最好条形统计图表示。( )
20.用4个小正方体摆一个几何体,如果从正面和侧面看到的都是,我们就可以确定这4个小正方体是怎样摆的。( )www.21-cn-jy.com
四、解答题
21.如下图,点A用数对(2,7)表示,点C用数对(5,9)表示。
(1)点B用数对( , )表示。
(2)画出三角形ABC绕点C逆时针旋转后的图形。
(3)画出三角形ABC向右下角平移后的图形,使得点的位置用数对(6,2)表示。
22.下面是护士为一位病人测量的体温统计折线图。
(1)护士每隔( )小时给该病人量一次体温。
(2)这位病人的最高体温是( )摄氏度,最低体温是( )摄氏度。
(3)从体温上观察,这位病人的病情是好转还是恶化?
23.在下图中,从图形A到图形B是怎样运动的 请你准确表述一下.
24.下面是某旅游景区去年接待游客情况统计图。
(1)去年两次旅游高峰,一次是( )月,另一次是( )月,这两个月的游客一共是( )万人。21cnjy.com
(2)去年游客人数最多的月份与最少的月份相差( )万人。
(3)去年游客月平均人数是( )万人。
(4)去年游客人数多于月平均人数的月份有( )个,少于月平均人数的月份有( )个。
(5)从这张统计图你还知道哪些信息?
25.下面表格中是李子轩和赵璐瑶五个月用于体育锻炼的月支出费用情况,请根据表中数据绘制出复式折线统计图。21·世纪*教育网
(1)从图中看,( )的体育锻炼月支出费用呈上升趋势。
(2)赵璐瑶这五个月用于体育锻炼的平均支出费用是( )元。
参考答案:
1.B
【分析】A.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
B.从正面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;21教育网
C.从正面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;2·1·c·n·j·y
D.从正面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【详解】A.从正面看到的形状是,从左面看到的形状是;
B.从正面看到的形状是,从左面看到的形状是;
C.从正面看到的形状是,从左面看到的形状是;
D.从正面看到的形状是,从左面看到的形状是。
故答案为:B
2.B
【分析】从上面看到的是,说明这个几何体的最下层是;从前面看到的是,说明这个几何体可能是、、;又因为这个几何体是由5个同样的小正方体搭成,所以这个几何体可能是或。再与四个选项进行对照可知,B选项是。
【详解】A.从前面看到的是,从上面看到的是。A选项错误。
B.从前面和上面看都是。B选项正确。
C.从前面看到的是,从上面看到的是。C选项错误。
D.从前面看到的是,从上面看到的是。D选项错误。
故答案为:B
【点睛】不同形状的几何体,从同一角度观察,得到的平面图形可能是相同的。
3.B
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。这个点为旋转中心,旋转的角度叫旋转角。物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。
【详解】根据分析可知,旋转过程中图案的变化规律是形状、大小都不改变,只是位置发生了变化。
故答案为:B
【点睛】正确理解旋转的意义与特征,是解答此题的关键。
4.C
【分析】物体的旋转有两个特点: 一个旋转中心,物体的形状不变。逐项分析是否具备这两个条件,即可选择。
【详解】A.钟摆形状不变,围绕一个中心左右摆动,属于旋转。
B.拧紧螺丝,螺丝形状不变,围绕螺母转动,属于旋转。
C.电梯的升降运动,没有旋转中心,虽然形状不变,但不属于旋转。
D.方向盘的转动,也是形状不变,有旋转中心,属于旋转。
故答案为:C
【点睛】本题考查旋转的定义,熟记旋转的定义是关键。
5.B
【分析】从正面看有5个小正方体,从左面看有4个正方体,则至少需要7个小正方体摆成;至多有两排第一排有5个小正方体,第二排有5个小正方体,据此解答即可。
【详解】5+5=10(个)
所以这个几何体至少要用7个小正方体摆成,至多要用10个小正方体摆成。
故答案为:B
【点睛】本题考查通过三视图确定几何体,明确从不同方向观察到的正方体的个数是解题的关键。
6.C
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。小猴子在A点时,看到房子的图片是,从A点绕房子逆时针转90°时,这时看到房子的图片是,从A点绕房子逆时针转180°时,这时看到房子的图片是,从A点绕房子逆时针转270°时,这时看到房子的图片是;据此解答。
【详解】根据分析得,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片依次为:
。
故答案为:C
【点睛】此题主要考查旋转及旋转现象,明确旋转的定义是解题的关键。
7. 小方 小丽
【分析】因为光是沿直线传播的,以光源为端点,过物体的边沿画射线,射线内的部分就是物体的影子,物体越靠近光源,射线所形成的角度发生变化,影子会越来越短;反之就越来越长。据此解答。21*cnjy*com
【详解】根据分析得,小方的影子比小丽的影子长,说明小方离路灯的位置远,小丽离路灯的位置近。
【点睛】本题考查了从不同方向观察物体和几何体,需要注意人的影子的长短与人遮挡光的面积的大小有关。
8. ③④⑤⑥⑦ ⑧ ②⑦
【分析】
从前面看是,说明这个几何体只有一层,排除⑧,在剩下的几何体中找出从前面能看到3个小正方形的即可。
从上面看是,说明这个几何体只有一行,只有⑧符合要求;
从左面看是,说明这个几何体有一层三行,只有②⑦符合要求。
【详解】
上面的图形中,从前面看是的有③④⑤⑥⑦,从上面看是的有⑧,从左面看是的有②⑦。
9. 小刚 小强 3 小刚 100 178m/min 145m/min
【详解】略
10. 逆 90 B 90 顺 90 D 180
【分析】根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数,某点的位置不动,其余各部分均绕某点按相同的方向旋转相同的度数。据此解答。【版权所有:21教育】
【详解】①号图形是绕A点按逆时针方向旋转了90°;
②号图形是绕B点按顺时针方向旋转了90°;
③号图形是绕C点按顺时针方向旋转了90°;
④号图形是绕D点按逆时针方向旋转了180°。
【点睛】本题考查了图形的旋转,注意旋转三要素:旋转中心、旋转方向、旋转角。
11.11
【分析】计算出一个正方形面的面积,再数出一共有多少个露在外面的面,代入数据用乘法计算即可。
【详解】1×1×11
=1×11
=11(平方厘米)
【点睛】掌握正方形的面积计算公式,并准确数出露在外面的面,这是解决此题的关键。
12. 7 10 11 12 10 8
【详解】略
13. 90 95
【分析】将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.众数是一组数据中出现次数最多的数;据此解答即可.【来源:21cnj*y.co*m】
【详解】将这组数据从小到大排列为:75、85、88、90、95、95、95;所以中位数是90;众数是95.
故答案为90;95.
14.7
【分析】从正面看有2层,下边1层3个小正方形,上边1层中间1个小正方形;从左面看有2层,下边1层2个小正方形,上边靠左1个小正方形,再考虑遮挡,画出示意图,数一数即可。
【详解】从正面看是,从左面看是,最多如图,用7块正方体积木摆出来的。
【点睛】关键是具有一定的空间想象能力,可以画一画示意图。
15.(1) 五 一
(2) 二 四
(3)5
(4)四
【分析】(1)一中的折线是实线,通过观察统计图可知,一中最高得分和最低得分的场次。
(2)二中的折线是虚线,通过观察统计图可知,二中最高得分和最低得分的场次。
(3)从统计图中找到第二场比赛时两队的成绩,用减法计算即可。
(4)求出每场比赛成绩的差值,进行比较,得出两队成绩相差最大的场次。
【详解】(1)55>54>50>48>46
一中最高得分是第五场,最低得分是第一场。
(2)53>51>50>48>45
二中最高得分是第二场,最低得分是第四场。
(3)53-48=5(分)
两个学校的篮球队第二场比赛时成绩相差5分。
(4)第一场成绩相差:50-46=4(分)
第二场成绩相差:53-48=5(分)
第三场成绩相差:50-48=2(分)
第四场成绩相差:54-45=9(分)
第五场成绩相差:55-51=4(分)
9>5>4>2
所以两个学校的篮球队成绩相差最大的是第四场比赛。
【点睛】理解掌握复式折线统计图的特点,从统计图中获取信息,并且能够根据统计图提供的信息解决有关的实际问题。21·cn·jy·com
16.√
【分析】钟表上的时针从12走到2,是按顺时针走的,因为一个圆可以看成一个周角,一共是360°,1小时是60分钟,每个小格是1分钟,对应的角度就是360÷60=6°.
【详解】从12走到2,一共走了10个小格,也就是旋转了60°.
17.√
【分析】平移是把一个物体整体沿着某一个方向移动一定的距离;旋转是将一个物体绕一点按某个方向转动一个角度;根据平移与旋转定义判断即可。
【详解】行驶的汽车车身运动是平移现象,汽车轮胎的运动是旋转现象,说法正确。
故答案为:√
【点睛】本题考查了学生对于平移和旋转的理解以及在实际生活中的应用。
18.√
【分析】该几何体从正面看到的图形是,说明该几何体至少有一行,这一行里有两层,两层都是2个小正方体;所以至少是需要4个小正方体;据此解答。
【详解】由分析可知:要摆出从正面看到的图形是的几何体,至少需要4个小正方体,所以原题说法正确。
故答案为:√
【点睛】本题考查了观察物体,关键是要掌握从不同角度观察到的立体图形的特点,分析出该立体图形的形状。
19.×
【分析】条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
【详解】一周的天气变化情况最好折线统计图表示,所以原题说法错误。
故答案为:×
【点睛】关键是熟悉条形统计图和折线统计图的特点,根据统计图的特点确定统计图。
20.√
【分析】用4个小正方体摆一个几何体,如果从正面和侧面看到的都是,则这个几何体摆了1层,占地面积是个正方形,即前边1行2个小正方体,后边1行2个小正方体,据此分析。
【详解】根据分析,摆出来的几何体如图,是可以确定这4个小正方体是怎样摆的。
故答案为:√
【点睛】关键是具有一定的空间想象能力,可以画一画示意图帮助理解。
21.(1)(2,9)
(2)(3)
【分析】(1)表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点
【详解】(1)点B用数对(2,9)表示。
(2)(3)
【点睛】本题考查了数对与位置,作旋转和平移后的图形,平移和旋转都是物体或图形的位置发生变化而形状、大小不变。区别在于,平移时物体沿直线运动,本身方向不发生改变;旋转是物体绕着某一点或轴运动,本身方向发生了变化。
22.(1)6;(2)39.5;36.8;(3)好转
【分析】(1)求出横坐标每日一格表示的时间即可;
(2)找出最高点和最低点的纵坐标即可。
(3)观察统计图,结合正常体温解答即可。
【详解】(1)护士每隔6小时给该病人量一次体温。
(2)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度。
(3)人体的正常体温是37℃,病人后来的体温稳定在这一水平线上,说明病情好转。
【点睛】此题考查了折线统计图的实际应用,能够根据问题从统计图中提取有效数学信息是解题关键。
23.图形A先绕点O逆时针旋转90度,再向右平移10格得到图形B.(图形A先向右平移10格,再绕点O'逆时针旋转90度得到图形B.)21世纪教育网版权所有
【详解】略
24.(1)4;10;19;
(2)8;
(3)5;
(4)3;6;
(5)1月到4月旅游景区去年接待游客数量呈上升趋势;4月到6月以及10月到12月旅游景区去年接待游客数量呈下降趋势。
【分析】(1)由折线统计图可知,折线的最高点一个是4月份9万人,一个是10月份10万人;
(2)由折线统计图可知,游客人数最多的是10月份10万人,游客人数最少是1月份2万人;
(3)用这组数据的和除以数据的个数,就是平均数;
(4)计算折线统计图中游客人数多于5万人的月份和少于5万人的月份各有多少个;
(5)折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况,根据折线的走势分析人数的增减变化情况即可。
【详解】(1)9+10=19(万人)
去年两次旅游高峰,一次是4月,另一次是10月,这两个月的游客一共是19万人。
(2)10-2=8(万人)
去年游客人数最多的月份与最少的月份相差8万人。
(3)(2+3+5+9+6+4+4+5+5+10+4+3)÷12
=60÷12
=5(万人)
(4)去年游客人数多于月平均人数的月份有:4月、5月、10月,一共3个;
去年游客人数少于月平均人数的月份有:1月、2月、6月、7月、11月、12月,一共6个。
(5)由折线统计图可知,1月到4月旅游景区去年接待游客数量呈上升趋势;4月到6月以及10月到12月旅游景区去年接待游客数量呈下降趋势。(答案不唯一)
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
25.图见详解
(1)赵璐瑶(2)74
【分析】填补复式折线统计图:根据统计表中的数据描点,在描的点旁边注上数据,李子轩支出用实线连线,赵璐瑶支出数用虚线连线;21*cnjy*com
(1)观察统计图可得:李子轩后四个月用于体育锻炼月支出费用呈下降趋势,赵璐瑶的体育锻炼月支出费用呈上升趋势;
(2)根据“平均数=总数÷份数”,求出赵璐瑶这五个月用于体育锻炼的平均支出费用。
【详解】作图如下:
(1)从图中看,赵璐瑶的体育锻炼月支出费用呈上升趋势;
(2)(60+70+80+75+85)÷5
=370÷5
=74(元)
【点睛】读取统计表中的数据,填补复式折线统计图,根据统计图信息解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
