2025人教版高中物理选择性必修第一册同步练习题(有解析)--第四章 光拔高练
文档属性
| 名称 | 2025人教版高中物理选择性必修第一册同步练习题(有解析)--第四章 光拔高练 |  | |
| 格式 | docx | ||
| 文件大小 | 958.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-06-05 15:32:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教版高中物理选择性必修第一册
综合拔高练
五年高考练
考点1 折射问题的分析与计算
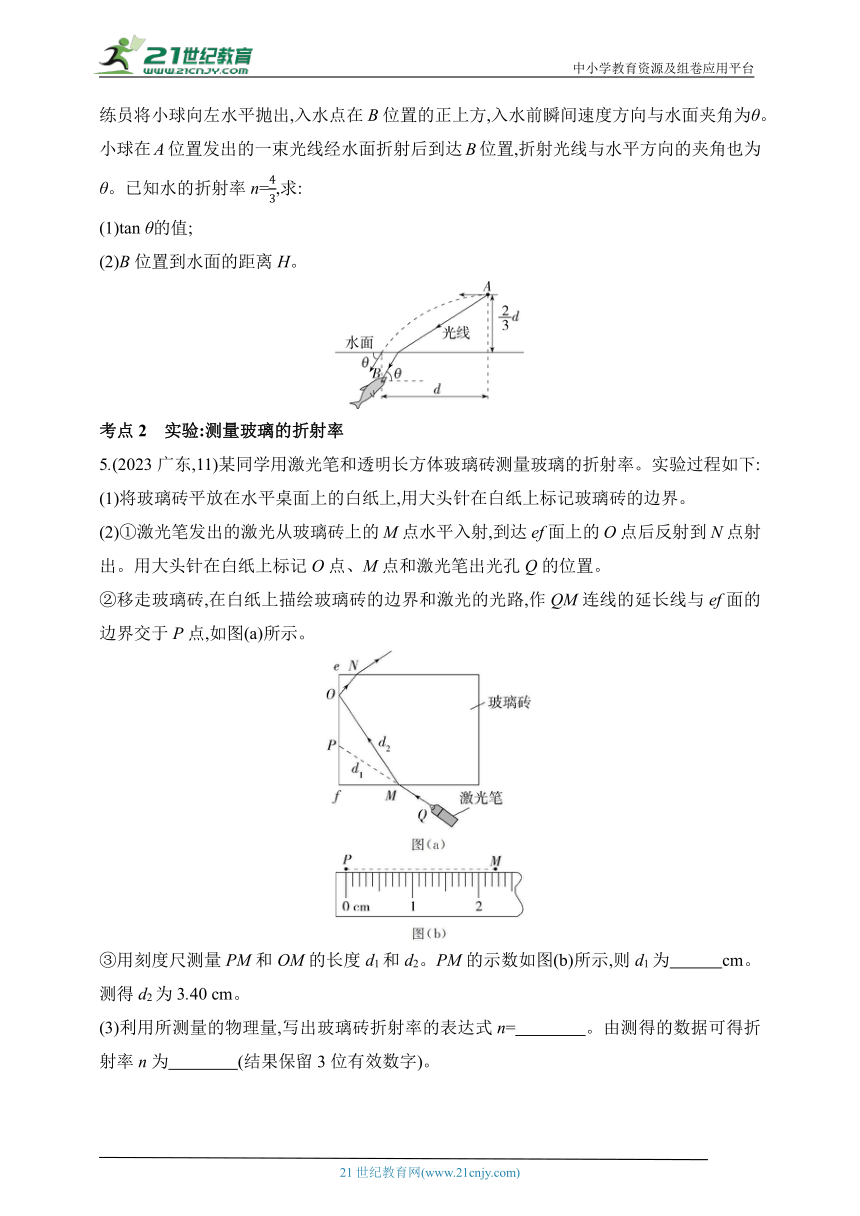
1.(2023江苏,5)地球表面附近空气的折射率随高度降低而增大,太阳光斜射向地面的过程中会发生弯曲。下列光路图中能描述该现象的是 ( )
2.[2023全国乙,34(2)]如图,一折射率为的棱镜的横截面为等腰直角三角形ABC,AB=AC=l,BC边所在底面上镀有一层反射膜。一细光束沿垂直于BC方向经AB边上的M点射入棱镜,若这束光被BC边反射后恰好射向顶点A,求M点到A点的距离。
3.(2022江苏,12)如图所示,两条距离为D的平行光线,以入射角θ从空气射入平静水面,反射光线与折射光线垂直。求:
(1)水的折射率n;
(2)两条折射光线之间的距离d。
4.(2022湖北,14)如图所示,水族馆训练员在训练海豚时,将一发光小球高举在水面上方的A位置,海豚的眼睛在B位置,A位置和B位置的水平距离为d,A位置离水面的高度为d。训练员将小球向左水平抛出,入水点在B位置的正上方,入水前瞬间速度方向与水面夹角为θ。小球在A位置发出的一束光线经水面折射后到达B位置,折射光线与水平方向的夹角也为θ。已知水的折射率n=,求:
(1)tan θ的值;
(2)B位置到水面的距离H。
考点2 实验:测量玻璃的折射率
5.(2023广东,11)某同学用激光笔和透明长方体玻璃砖测量玻璃的折射率。实验过程如下:
(1)将玻璃砖平放在水平桌面上的白纸上,用大头针在白纸上标记玻璃砖的边界。
(2)①激光笔发出的激光从玻璃砖上的M点水平入射,到达ef面上的O点后反射到N点射出。用大头针在白纸上标记O点、M点和激光笔出光孔Q的位置。
②移走玻璃砖,在白纸上描绘玻璃砖的边界和激光的光路,作QM连线的延长线与ef面的边界交于P点,如图(a)所示。
③用刻度尺测量PM和OM的长度d1和d2。PM的示数如图(b)所示,则d1为 cm。测得d2为3.40 cm。
(3)利用所测量的物理量,写出玻璃砖折射率的表达式n= 。由测得的数据可得折射率n为 (结果保留3位有效数字)。
(4)相对误差的计算式为δ=×100%。为了减小d1、d2测量的相对误差,实验中激光在M点入射时应尽量使入射角 。
6.(2023海南,14)如图所示,在用激光测玻璃砖折射率的实验中,玻璃砖与光屏P平行放置,从另一侧用激光笔以一定角度照射,此时在光屏上的S1处有激光点,移走玻璃砖,光点移到S2处。
(1)请在图中画出激光束经玻璃砖折射后完整的光路图;
(2)已经测出AB=l1,OA=l2,S1S2=l3,则折射率n= (用l1、l2、l3表示);
(3)若改用宽度比ab更小的玻璃砖做实验,则S1S2间的距离会 (填“变大”“变小”或“不变”)。
考点3 全反射问题的分析与计算
7.(多选题)(2023湖南,7)一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是 ( )
A.水的折射率为
B.水的折射率为
C.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角小于60°
D.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角大于60°
8.(2023湖北,6)如图所示,楔形玻璃的横截面POQ的顶角为30°,OP边上的点光源S到顶点O的距离为d,垂直于OP边的光线SN在OQ边的折射角为45°。不考虑多次反射,OQ边上有光射出部分的长度为 ( )
A.d B.d C.d D.d
9.(2023浙江6月选考,13)在水池底部水平放置三条细灯带构成的等腰直角三角形发光体,直角边的长度为0.9 m,水的折射率n=,细灯带到水面的距离h= m,则有光射出的水面形状(用阴影表示)为 ( )
A B
C D
10.[2022重庆,16(2)]如图所示,水面上有一透明均质球,上半球露出水面,下半球内竖直中心轴上有红、蓝两种单色灯(可视为点光源),均质球对两种色光的折射率分别为n红和n蓝。为使从光源照射到上半球面的光,都能发生折射(不考虑光线在球内反射后的折射),若红灯到水面的最大距离为h红。
①求蓝灯到水面的最大距离;
②两灯都装在各自到水面的最大距离处,蓝灯在红灯的上方还是下方 为什么
11.(2023山东,16)一种反射式光纤位移传感器可以实现微小位移测量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝M、N,相距为d,直径均为2a,折射率为n(n<)。M、N下端横截面平齐且与被测物体表面平行。激光在M内多次全反射后从下端面射向被测物体,经被测物体表面镜面反射至N下端面,N下端面被照亮的面积与玻璃丝下端面到被测物体距离有关。
(1)从M下端面出射的光与竖直方向的最大偏角为θ,求θ的正弦值;
(2)被测物体自上而下微小移动,使N下端面从刚能接收反射激光到恰好全部被照亮,求玻璃丝下端面到被测物体距离b的相应范围(只考虑在被测物体表面反射一次的光线)。
考点4 光的干涉
12.(2023江苏,6)用某种单色光进行双缝干涉实验,在屏上观察到的干涉条纹如图甲所示,改变双缝间的距离后,干涉条纹如图乙所示,图中虚线是亮纹中心的位置。则双缝间的距离变为原来的 ( )
A.倍 B.倍 C.2倍 D.3倍
13.(2023河北,2)制造某型芯片所使用的银灰色硅片覆上一层厚度均匀的无色透明薄膜后,在自然光照射下硅片呈现深紫色。关于此现象,下列说法正确的是 ( )
A.上述现象与彩虹的形成原理相同
B.光在薄膜的下表面发生了全反射
C.薄膜上下表面的反射光发生了干涉
D.薄膜厚度发生变化,硅片总呈现深紫色
14.(2023山东,5)如图所示为一种干涉热膨胀仪原理图。G为标准石英环,C为待测柱形样品,C的上表面与上方标准平面石英板之间存在劈形空气层。用单色平行光垂直照射上方石英板,会形成干涉条纹。已知C的膨胀系数小于G的膨胀系数,当温度升高时,下列说法正确的是 ( )
A.劈形空气层的厚度变大,条纹向左移动
B.劈形空气层的厚度变小,条纹向左移动
C.劈形空气层的厚度变大,条纹向右移动
D.劈形空气层的厚度变小,条纹向右移动
三年模拟练
应用实践
1.(2024福建宁德一模)某同学做测定玻璃折射率的实验,正确操作后,作出图示光路并测出相关角度α、θ。在用获得的多组数据α和θ作出的下列图像中,可能正确的是 ( )
2.(2024皖豫名校联盟联考)如图所示,一块足够长两面平行玻璃砖对红色光的折射率为n=,一束红色光垂直射到该玻璃砖所用的上表面某点P时,穿过该玻璃砖所用的时间为t。若该单色光以45°的入射角斜射到P点,则该束光从下表面射出所需的时间是 ( )
A.t B.t C.t D.t
3.(2024河北沧州联考)地球大气层对光线的折射会使我们提前看到日出,称为蒙气差效应。物理老师制作了教具来演示这一效应,如图所示为教具中“地球”的北极俯视图,“地球”半径15 cm,绕“地轴”逆时针自转周期为2 min。折射率为的“大气层”厚度为10 cm,以平行光入射充当“太阳光”,则由于“大气层”的存在,“地球赤道”上的点相对于没有大气层将提前约多长时间看到“太阳光” ( )
A.5 s B.5.3 s
C.10 s D.10.6 s
4.(2024江苏盐城期中)如图所示,玻璃砖的横截面ABC是直角三角形,∠A=30°,BC边长为L,BC为镜面。一束与AC成37°的单色光从AC边上的G点射入玻璃砖,在镜面BC边的反射光线EF与AC平行,E是BC的中点。已知真空中光速为c。(sin 37°=0.6,cos 37°=0.8)求:
(1)玻璃砖的折射率n;
(2)该光束第一次射出玻璃砖的出射角θ;
(3)该光束从射入玻璃砖到第一次射出玻璃砖的传播时间t。
5.(2024江苏南京临江高级中学月考)如图,岸上竖直放置标尺杆F,某潜水员处于海面下E点,他观察岸上的标尺杆F,仅能看到杆的一半刻度。已知标尺杆F长6 m,标尺杆F距离岸边A点4 m;E点距离海岸边7 m、海面4 m;海面CD到海岸AB的高度为3 m。求:
(1)海水的折射率;
(2)若涨潮时海面CD上升至与海岸AB平齐,潜水员仍处于海面下E点,此时能看到的标尺杆长度。
6.(2024湖北部分重点高中联考)如图所示长方体玻璃砖ABCD-A'B'C'D',长AB为6 cm,宽与高均为2 cm。AB边上有一单色光源S,玻璃对该单色光的折射率为,当右侧面BCC'B'恰好全部都有光线射出时,求:
(1)光源S离B点的距离是多少;
(2)左侧面ADD'A'有光线射出的面积是多少。
迁移创新
7.某半径为r的类地行星表面有一单色点光源P,其发出的各方向的光经过厚度为(-1)r、折射率n=2的均匀行星大气层射向太空。取包含P和行星中心O的某一截面(如图所示),设此截面内,一卫星探测器在半径为的轨道上绕行星做匀速圆周运动。忽略行星表面对光的反射。求:
(1)从P点发出的光入射到大气层外表面处时,发生全反射的临界角;
(2)大气层外表面发光区域在截面上形成的弧长;
(3)卫星探测器运行时,只能在轨道某些部分观测到光,则这部分轨道的弧长。
答案与分层梯度式解析
综合拔高练
五年高考练
1.A 根据折射定律有n上 sin θ上=n下 sin θ下,由于地球表面附近空气的折射率随高度降低而增大,则n下>n上,则θ下逐渐减小,画出光路图如图所示,则光线应逐渐趋于竖直方向,选项A正确。
2.答案 l
解析 光束由M点射入发生折射,经BC边反射后经过A点,作出光路图如图所示,
光线垂直于BC方向射入,根据几何关系可知入射角i=45°;
由于棱镜的折射率为,根据n=,得sin r=,则折射角r=30°;
∠BMO=60°,因为∠B=45°,所以光在BC面的入射角θ=90°-(180°-60°-45°)=15°,根据反射定律可知∠MOA=2θ=30°
根据几何关系可知∠BAO=30°,即△MAO为等腰三角形,则=
又因为△BOM与△COA相似,故有=
由题知AB=AC=l
联立可得BM=AC=l
所以M点到A点的距离MA=l-BM=l
一题多解 在△BMO中,根据正弦定理有=,MO=MA,BM=l-MA,sin 75°= sin (45°+30°)=,解得MA=l。
3.答案 (1)tan θ (2)D tan θ
解析 (1)由几何关系可知折射角α=90°-θ,则折射率n==tan θ。
(2)如图所示,由几何关系可知=,所以d=D=D tan θ。
4.答案 (1) (2)d
解析 (1)小球做平抛运动,设初速度为v0、在空中飞行时间为t,则
水平方向上d=v0t
竖直方向上=t
再由速度合成与分解有tan θ=
解得tan θ=
(2)设光线在水面的入射角为θ1,由折射定律有
n=
再由图中几何关系有
d=+ tan θ1
联立解得H=d
5.答案 (2)2.25(2.24~2.26均可)
(3) 1.51(1.50~1.52均可) (4)稍小一些
解析 (2)③刻度尺的最小刻度为1 mm,由图可知,d1为2.25 cm。
(3)玻璃砖折射率的表达式n====,代入数据可知n=≈1.51。
(4)相对误差的计算式为δ=×100%,为了减小d1、d2测量的相对误差,实验中d1、d2要尽量稍大一些,即激光在M点入射时应尽量使入射角稍小一些。
6.答案 (1)图见解析 (2) (3)变小
解析 (1)根据题意画出光路图如图所示。
(2)设光线在C点的入射角为θ、折射角为α,则根据折射定律有n sin θ= sin α
由于光线穿过平行玻璃砖的出射光线和入射光线平行,则S1S2=CB,(破题关键)根据几何关系可知sin θ=,sin α=,联立解得n=。
(3)若改用宽度比ab更小的玻璃砖做实验,则画出光路图如图所示,可看出S1S2间的距离变小。
7.BC 他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,则说明α=41°时激光恰好发生全反射,如图甲所示,则sin 49°=,则n=,选项A错误,B正确;当他以α=60°向水面发射激光时,入射角i1=30°,如图乙所示,则根据折射定律有n sin i1= sin i2,折射角i2大于30°,则岸上救援人员接收激光光束的方向与水面夹角小于60°,选项C正确,D错误。
8.C 在N点发生折射时,由几何关系知入射角为30°,则折射率n==,由sin C=知,全反射临界角C=45°,OQ边上有光射出部分如图中AB区域,由几何关系可知SD=,则AB=2SD=d,C正确。
9.C 全反射临界角的正弦值为sin C==,根据三角函数知识得cos C=, tan C==,假设在距水面h处有一点光源,则其在水面照亮的区域为圆形,如图甲所示,设其半径为R,则tan C=,解得R=0.3 m。细灯带可看成由一系列点光源组成,由于l sin 45°
10.答案 ①h红 ②见解析
关键点拨 如图所示,由=可知,θ越大,入射角i越大,当光从光源照到与水面相平的圆周上的点时,入射角最大。
解析 ①为使从光源照射到上半球面的光都能发生折射,以红光为例,当入射角最大达到临界角C红时,光线恰好垂直水面折射出去,光路图如图所示
假设球半径为R,根据全反射临界角公式可知sin C红=
由几何关系可知tan C红=
同理可知对蓝光有sin C蓝=,tan C蓝=
两式联立解得h蓝=h红
②同种介质对蓝光的折射率大于对红光的折射率,即n蓝>n红>1,可知h蓝=·h红11.答案 (1) (2)≤b≤
思路点拨 (1)当光在M的侧面刚好发生全反射时,从M下端面出射的光与竖直方向夹角最大。
(2)当光从M下端面的最右侧以θ角射出时,反射光线照射到N下端面的最左侧和最右侧,分别对应被测物体的最高位置和最低位置。
(1)激光在M内侧壁上刚好发生全反射时,入射角和反射角最小,在下端面的入射角最大,折射角即出射的光与竖直方向的偏角最大,则sin C=
n=
解得sin θ=
(2)激光在M内侧壁刚好发生全反射并从下端面最右端射出,经被测物体反射后刚好射到N下端面最左端时b最小,刚好射到N下端面最右端时b最大,(破题关键)则
bmin==
bmax==
则b的取值范围是≤b≤
12.B 双缝干涉的条纹间距与波长的关系为Δx=λ,由题图知Δx乙=2Δx甲,则d乙=d甲,选项B正确。
13.C 题干所述现象是光的干涉造成的,彩虹的形成原理主要为光的折射,二者形成原理不相同,选项A错误;硅片呈现深紫色的原因是薄膜的厚度正好使紫光在薄膜上下表面的反射光发生干涉,振动加强,选项B错误,C正确;根据光的干涉中相互加强的条件,可知当薄膜的厚度发生变化时,满足加强条件的波长也会发生改变,导致硅片呈现不同的颜色,选项D错误。
14.A 由题知,C的膨胀系数小于G的膨胀系数,当温度升高时,G增长的高度大于C增长的高度,则劈形空气层的厚度变大,(破题关键)如图所示,同一厚度的空气膜向劈尖移动,则条纹向左移动,选项A正确。
一题多解 空气膜不同厚度处的干涉条纹对应两束干涉光的不同路程差,若设空气膜厚度为d,光的波长为λ,则干涉条纹处2d=kλ(k=0,1,2,…),若厚度d增加,则同一位置处干涉条纹的相应级次会增大,故条纹将向左移动,选项A正确。
三年模拟练
1.B 根据折射定律可得折射律n==,故cos θ=·cos α,故可能正确的图像是B。
2.B 设光在玻璃砖中的速度为v,平行玻璃砖厚度为d,v=,若该单色光以45°的入射角斜射到P点,由n=,解得折射角θ=30°,单色光在玻璃砖中传播距离为x==d,该束光从下表面射出所需的时间t'===t,选项B正确。
3.B 光路图如图所示,A点观察到第一道曙光时,设光在大气层外的入射角为α,进入大气层后的折射角为β,由几何关系可得sin β===,解得β=37°。根据折射律n=,解得sin α=,即α=53°。若无大气层,A点需随地球转动到B时才能观察到日出,(破题关键)由几何关系,∠AOB=(90°-β)-(90°-α)=16°,故提前的时间为t=T≈5.3 s,选项B正确。
4.答案 (1)1.6 (2)53° (3)
解析 (1)AC界面上,由几何关系可知入射角为i=53°
折射角为γ=30°
则折射率为n=
解得n=1.6
(2)在F点,入射角为i'=60°
可知sin i'>
即在F点发生全反射(破题关键),光线在AC面的入射角为i″=30°
在AC面发生折射,由n=
解得θ=53°
(3)光束在玻璃中的传播速度为v=
由几何关系可知,光束在玻璃中的路程为d=L+L+L=2L
解得光束在玻璃中传播时间为t===
5.答案 (1) (2)(6-) m
解析 (1)根据题意可得,最低可以观察位置的光路图如图所示
根据几何关系有∠PAB=∠AOD
由于PB=AD=3 m
则OD=AB=4 m
QO=QD-OD=7 m-4 m=3 m
则有sin β==,sin α==
根据折射定律可得,海水的折射率为n==
(2)若涨潮时海面CD上升至与海岸AB平齐,潜水员仍处于海面下E点,此时最低可以观察位置的光路图如图所示
设HB等于x,由几何知识有sin i=
sin r=
根据折射定律有n==
联立解得x= m
则此时能看到的标尺杆长度为l=(6-) m
6.答案 (1)4 cm (2) cm2
关键点拨 (1)若沿SC'的光线恰好发生全反射,则右侧面恰好均有光射出。
(2)若光线在左侧面的M点刚好发生全反射,则以A点为圆心、AM为半径,在ADD'A'面内的圆弧内均有光线射出。
解析 (1)当右侧面恰好全部都有光线射出时,C'点恰好发生全反射,
此时C'点的入射角记为θ,有sin θ==
可得tan θ=
在△SBC'中tan θ=
得SB===4 cm
(2)由(1)中的结论可得AS=AB-SB=2 cm
设光线在左侧面的M点刚好发生全反射(解题技法),M点到A点的距离为r,则有
tan θ=
解得r= cm
则以A点为圆心、AM为半径,在ADD'A'面内的圆弧内均有光线射出,故左侧面有光线射出的面积为S=πr2= cm2
7.答案 (1)30° (2) (3)
解析 (1)从P点发出的光入射到大气层外表面处时,发生全反射的临界角C满足sin C=,
解得C=30°
(2)当P点发出的光线在大气层外表面恰好发生全反射时,光路如图所示。
由正弦定理可得=,解得α=135°
故从P点射出的光线在大气层外表面恰好发生全反射时,光线PB与OP延长线的夹角为45°,大气层外表面发光区域在截面上对应的圆心角为
β=2×(45°-C)=30°
故发光区域在截面上形成的弧长为
l=×2π×r=
(3)如图所示,临界光线从B点射向卫星轨道上的C点,在直角△OBC中,由几何关系可得
cos ∠BOC==,解得∠BOC=15°
即轨道上能观测到光的部分对应的圆心角为60°,对应的轨道弧长为l'=×2π×=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版高中物理选择性必修第一册
综合拔高练
五年高考练
考点1 折射问题的分析与计算
1.(2023江苏,5)地球表面附近空气的折射率随高度降低而增大,太阳光斜射向地面的过程中会发生弯曲。下列光路图中能描述该现象的是 ( )
2.[2023全国乙,34(2)]如图,一折射率为的棱镜的横截面为等腰直角三角形ABC,AB=AC=l,BC边所在底面上镀有一层反射膜。一细光束沿垂直于BC方向经AB边上的M点射入棱镜,若这束光被BC边反射后恰好射向顶点A,求M点到A点的距离。
3.(2022江苏,12)如图所示,两条距离为D的平行光线,以入射角θ从空气射入平静水面,反射光线与折射光线垂直。求:
(1)水的折射率n;
(2)两条折射光线之间的距离d。
4.(2022湖北,14)如图所示,水族馆训练员在训练海豚时,将一发光小球高举在水面上方的A位置,海豚的眼睛在B位置,A位置和B位置的水平距离为d,A位置离水面的高度为d。训练员将小球向左水平抛出,入水点在B位置的正上方,入水前瞬间速度方向与水面夹角为θ。小球在A位置发出的一束光线经水面折射后到达B位置,折射光线与水平方向的夹角也为θ。已知水的折射率n=,求:
(1)tan θ的值;
(2)B位置到水面的距离H。
考点2 实验:测量玻璃的折射率
5.(2023广东,11)某同学用激光笔和透明长方体玻璃砖测量玻璃的折射率。实验过程如下:
(1)将玻璃砖平放在水平桌面上的白纸上,用大头针在白纸上标记玻璃砖的边界。
(2)①激光笔发出的激光从玻璃砖上的M点水平入射,到达ef面上的O点后反射到N点射出。用大头针在白纸上标记O点、M点和激光笔出光孔Q的位置。
②移走玻璃砖,在白纸上描绘玻璃砖的边界和激光的光路,作QM连线的延长线与ef面的边界交于P点,如图(a)所示。
③用刻度尺测量PM和OM的长度d1和d2。PM的示数如图(b)所示,则d1为 cm。测得d2为3.40 cm。
(3)利用所测量的物理量,写出玻璃砖折射率的表达式n= 。由测得的数据可得折射率n为 (结果保留3位有效数字)。
(4)相对误差的计算式为δ=×100%。为了减小d1、d2测量的相对误差,实验中激光在M点入射时应尽量使入射角 。
6.(2023海南,14)如图所示,在用激光测玻璃砖折射率的实验中,玻璃砖与光屏P平行放置,从另一侧用激光笔以一定角度照射,此时在光屏上的S1处有激光点,移走玻璃砖,光点移到S2处。
(1)请在图中画出激光束经玻璃砖折射后完整的光路图;
(2)已经测出AB=l1,OA=l2,S1S2=l3,则折射率n= (用l1、l2、l3表示);
(3)若改用宽度比ab更小的玻璃砖做实验,则S1S2间的距离会 (填“变大”“变小”或“不变”)。
考点3 全反射问题的分析与计算
7.(多选题)(2023湖南,7)一位潜水爱好者在水下活动时,利用激光器向岸上救援人员发射激光信号,设激光光束与水面的夹角为α,如图所示。他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,下列说法正确的是 ( )
A.水的折射率为
B.水的折射率为
C.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角小于60°
D.当他以α=60°向水面发射激光时,岸上救援人员接收激光光束的方向与水面夹角大于60°
8.(2023湖北,6)如图所示,楔形玻璃的横截面POQ的顶角为30°,OP边上的点光源S到顶点O的距离为d,垂直于OP边的光线SN在OQ边的折射角为45°。不考虑多次反射,OQ边上有光射出部分的长度为 ( )
A.d B.d C.d D.d
9.(2023浙江6月选考,13)在水池底部水平放置三条细灯带构成的等腰直角三角形发光体,直角边的长度为0.9 m,水的折射率n=,细灯带到水面的距离h= m,则有光射出的水面形状(用阴影表示)为 ( )
A B
C D
10.[2022重庆,16(2)]如图所示,水面上有一透明均质球,上半球露出水面,下半球内竖直中心轴上有红、蓝两种单色灯(可视为点光源),均质球对两种色光的折射率分别为n红和n蓝。为使从光源照射到上半球面的光,都能发生折射(不考虑光线在球内反射后的折射),若红灯到水面的最大距离为h红。
①求蓝灯到水面的最大距离;
②两灯都装在各自到水面的最大距离处,蓝灯在红灯的上方还是下方 为什么
11.(2023山东,16)一种反射式光纤位移传感器可以实现微小位移测量,其部分原理简化如图所示。两光纤可等效为圆柱状玻璃丝M、N,相距为d,直径均为2a,折射率为n(n<)。M、N下端横截面平齐且与被测物体表面平行。激光在M内多次全反射后从下端面射向被测物体,经被测物体表面镜面反射至N下端面,N下端面被照亮的面积与玻璃丝下端面到被测物体距离有关。
(1)从M下端面出射的光与竖直方向的最大偏角为θ,求θ的正弦值;
(2)被测物体自上而下微小移动,使N下端面从刚能接收反射激光到恰好全部被照亮,求玻璃丝下端面到被测物体距离b的相应范围(只考虑在被测物体表面反射一次的光线)。
考点4 光的干涉
12.(2023江苏,6)用某种单色光进行双缝干涉实验,在屏上观察到的干涉条纹如图甲所示,改变双缝间的距离后,干涉条纹如图乙所示,图中虚线是亮纹中心的位置。则双缝间的距离变为原来的 ( )
A.倍 B.倍 C.2倍 D.3倍
13.(2023河北,2)制造某型芯片所使用的银灰色硅片覆上一层厚度均匀的无色透明薄膜后,在自然光照射下硅片呈现深紫色。关于此现象,下列说法正确的是 ( )
A.上述现象与彩虹的形成原理相同
B.光在薄膜的下表面发生了全反射
C.薄膜上下表面的反射光发生了干涉
D.薄膜厚度发生变化,硅片总呈现深紫色
14.(2023山东,5)如图所示为一种干涉热膨胀仪原理图。G为标准石英环,C为待测柱形样品,C的上表面与上方标准平面石英板之间存在劈形空气层。用单色平行光垂直照射上方石英板,会形成干涉条纹。已知C的膨胀系数小于G的膨胀系数,当温度升高时,下列说法正确的是 ( )
A.劈形空气层的厚度变大,条纹向左移动
B.劈形空气层的厚度变小,条纹向左移动
C.劈形空气层的厚度变大,条纹向右移动
D.劈形空气层的厚度变小,条纹向右移动
三年模拟练
应用实践
1.(2024福建宁德一模)某同学做测定玻璃折射率的实验,正确操作后,作出图示光路并测出相关角度α、θ。在用获得的多组数据α和θ作出的下列图像中,可能正确的是 ( )
2.(2024皖豫名校联盟联考)如图所示,一块足够长两面平行玻璃砖对红色光的折射率为n=,一束红色光垂直射到该玻璃砖所用的上表面某点P时,穿过该玻璃砖所用的时间为t。若该单色光以45°的入射角斜射到P点,则该束光从下表面射出所需的时间是 ( )
A.t B.t C.t D.t
3.(2024河北沧州联考)地球大气层对光线的折射会使我们提前看到日出,称为蒙气差效应。物理老师制作了教具来演示这一效应,如图所示为教具中“地球”的北极俯视图,“地球”半径15 cm,绕“地轴”逆时针自转周期为2 min。折射率为的“大气层”厚度为10 cm,以平行光入射充当“太阳光”,则由于“大气层”的存在,“地球赤道”上的点相对于没有大气层将提前约多长时间看到“太阳光” ( )
A.5 s B.5.3 s
C.10 s D.10.6 s
4.(2024江苏盐城期中)如图所示,玻璃砖的横截面ABC是直角三角形,∠A=30°,BC边长为L,BC为镜面。一束与AC成37°的单色光从AC边上的G点射入玻璃砖,在镜面BC边的反射光线EF与AC平行,E是BC的中点。已知真空中光速为c。(sin 37°=0.6,cos 37°=0.8)求:
(1)玻璃砖的折射率n;
(2)该光束第一次射出玻璃砖的出射角θ;
(3)该光束从射入玻璃砖到第一次射出玻璃砖的传播时间t。
5.(2024江苏南京临江高级中学月考)如图,岸上竖直放置标尺杆F,某潜水员处于海面下E点,他观察岸上的标尺杆F,仅能看到杆的一半刻度。已知标尺杆F长6 m,标尺杆F距离岸边A点4 m;E点距离海岸边7 m、海面4 m;海面CD到海岸AB的高度为3 m。求:
(1)海水的折射率;
(2)若涨潮时海面CD上升至与海岸AB平齐,潜水员仍处于海面下E点,此时能看到的标尺杆长度。
6.(2024湖北部分重点高中联考)如图所示长方体玻璃砖ABCD-A'B'C'D',长AB为6 cm,宽与高均为2 cm。AB边上有一单色光源S,玻璃对该单色光的折射率为,当右侧面BCC'B'恰好全部都有光线射出时,求:
(1)光源S离B点的距离是多少;
(2)左侧面ADD'A'有光线射出的面积是多少。
迁移创新
7.某半径为r的类地行星表面有一单色点光源P,其发出的各方向的光经过厚度为(-1)r、折射率n=2的均匀行星大气层射向太空。取包含P和行星中心O的某一截面(如图所示),设此截面内,一卫星探测器在半径为的轨道上绕行星做匀速圆周运动。忽略行星表面对光的反射。求:
(1)从P点发出的光入射到大气层外表面处时,发生全反射的临界角;
(2)大气层外表面发光区域在截面上形成的弧长;
(3)卫星探测器运行时,只能在轨道某些部分观测到光,则这部分轨道的弧长。
答案与分层梯度式解析
综合拔高练
五年高考练
1.A 根据折射定律有n上 sin θ上=n下 sin θ下,由于地球表面附近空气的折射率随高度降低而增大,则n下>n上,则θ下逐渐减小,画出光路图如图所示,则光线应逐渐趋于竖直方向,选项A正确。
2.答案 l
解析 光束由M点射入发生折射,经BC边反射后经过A点,作出光路图如图所示,
光线垂直于BC方向射入,根据几何关系可知入射角i=45°;
由于棱镜的折射率为,根据n=,得sin r=,则折射角r=30°;
∠BMO=60°,因为∠B=45°,所以光在BC面的入射角θ=90°-(180°-60°-45°)=15°,根据反射定律可知∠MOA=2θ=30°
根据几何关系可知∠BAO=30°,即△MAO为等腰三角形,则=
又因为△BOM与△COA相似,故有=
由题知AB=AC=l
联立可得BM=AC=l
所以M点到A点的距离MA=l-BM=l
一题多解 在△BMO中,根据正弦定理有=,MO=MA,BM=l-MA,sin 75°= sin (45°+30°)=,解得MA=l。
3.答案 (1)tan θ (2)D tan θ
解析 (1)由几何关系可知折射角α=90°-θ,则折射率n==tan θ。
(2)如图所示,由几何关系可知=,所以d=D=D tan θ。
4.答案 (1) (2)d
解析 (1)小球做平抛运动,设初速度为v0、在空中飞行时间为t,则
水平方向上d=v0t
竖直方向上=t
再由速度合成与分解有tan θ=
解得tan θ=
(2)设光线在水面的入射角为θ1,由折射定律有
n=
再由图中几何关系有
d=+ tan θ1
联立解得H=d
5.答案 (2)2.25(2.24~2.26均可)
(3) 1.51(1.50~1.52均可) (4)稍小一些
解析 (2)③刻度尺的最小刻度为1 mm,由图可知,d1为2.25 cm。
(3)玻璃砖折射率的表达式n====,代入数据可知n=≈1.51。
(4)相对误差的计算式为δ=×100%,为了减小d1、d2测量的相对误差,实验中d1、d2要尽量稍大一些,即激光在M点入射时应尽量使入射角稍小一些。
6.答案 (1)图见解析 (2) (3)变小
解析 (1)根据题意画出光路图如图所示。
(2)设光线在C点的入射角为θ、折射角为α,则根据折射定律有n sin θ= sin α
由于光线穿过平行玻璃砖的出射光线和入射光线平行,则S1S2=CB,(破题关键)根据几何关系可知sin θ=,sin α=,联立解得n=。
(3)若改用宽度比ab更小的玻璃砖做实验,则画出光路图如图所示,可看出S1S2间的距离变小。
7.BC 他发现只有当α大于41°时,岸上救援人员才能收到他发出的激光光束,则说明α=41°时激光恰好发生全反射,如图甲所示,则sin 49°=,则n=,选项A错误,B正确;当他以α=60°向水面发射激光时,入射角i1=30°,如图乙所示,则根据折射定律有n sin i1= sin i2,折射角i2大于30°,则岸上救援人员接收激光光束的方向与水面夹角小于60°,选项C正确,D错误。
8.C 在N点发生折射时,由几何关系知入射角为30°,则折射率n==,由sin C=知,全反射临界角C=45°,OQ边上有光射出部分如图中AB区域,由几何关系可知SD=,则AB=2SD=d,C正确。
9.C 全反射临界角的正弦值为sin C==,根据三角函数知识得cos C=, tan C==,假设在距水面h处有一点光源,则其在水面照亮的区域为圆形,如图甲所示,设其半径为R,则tan C=,解得R=0.3 m。细灯带可看成由一系列点光源组成,由于l sin 45°
10.答案 ①h红 ②见解析
关键点拨 如图所示,由=可知,θ越大,入射角i越大,当光从光源照到与水面相平的圆周上的点时,入射角最大。
解析 ①为使从光源照射到上半球面的光都能发生折射,以红光为例,当入射角最大达到临界角C红时,光线恰好垂直水面折射出去,光路图如图所示
假设球半径为R,根据全反射临界角公式可知sin C红=
由几何关系可知tan C红=
同理可知对蓝光有sin C蓝=,tan C蓝=
两式联立解得h蓝=h红
②同种介质对蓝光的折射率大于对红光的折射率,即n蓝>n红>1,可知h蓝=·h红
思路点拨 (1)当光在M的侧面刚好发生全反射时,从M下端面出射的光与竖直方向夹角最大。
(2)当光从M下端面的最右侧以θ角射出时,反射光线照射到N下端面的最左侧和最右侧,分别对应被测物体的最高位置和最低位置。
(1)激光在M内侧壁上刚好发生全反射时,入射角和反射角最小,在下端面的入射角最大,折射角即出射的光与竖直方向的偏角最大,则sin C=
n=
解得sin θ=
(2)激光在M内侧壁刚好发生全反射并从下端面最右端射出,经被测物体反射后刚好射到N下端面最左端时b最小,刚好射到N下端面最右端时b最大,(破题关键)则
bmin==
bmax==
则b的取值范围是≤b≤
12.B 双缝干涉的条纹间距与波长的关系为Δx=λ,由题图知Δx乙=2Δx甲,则d乙=d甲,选项B正确。
13.C 题干所述现象是光的干涉造成的,彩虹的形成原理主要为光的折射,二者形成原理不相同,选项A错误;硅片呈现深紫色的原因是薄膜的厚度正好使紫光在薄膜上下表面的反射光发生干涉,振动加强,选项B错误,C正确;根据光的干涉中相互加强的条件,可知当薄膜的厚度发生变化时,满足加强条件的波长也会发生改变,导致硅片呈现不同的颜色,选项D错误。
14.A 由题知,C的膨胀系数小于G的膨胀系数,当温度升高时,G增长的高度大于C增长的高度,则劈形空气层的厚度变大,(破题关键)如图所示,同一厚度的空气膜向劈尖移动,则条纹向左移动,选项A正确。
一题多解 空气膜不同厚度处的干涉条纹对应两束干涉光的不同路程差,若设空气膜厚度为d,光的波长为λ,则干涉条纹处2d=kλ(k=0,1,2,…),若厚度d增加,则同一位置处干涉条纹的相应级次会增大,故条纹将向左移动,选项A正确。
三年模拟练
1.B 根据折射定律可得折射律n==,故cos θ=·cos α,故可能正确的图像是B。
2.B 设光在玻璃砖中的速度为v,平行玻璃砖厚度为d,v=,若该单色光以45°的入射角斜射到P点,由n=,解得折射角θ=30°,单色光在玻璃砖中传播距离为x==d,该束光从下表面射出所需的时间t'===t,选项B正确。
3.B 光路图如图所示,A点观察到第一道曙光时,设光在大气层外的入射角为α,进入大气层后的折射角为β,由几何关系可得sin β===,解得β=37°。根据折射律n=,解得sin α=,即α=53°。若无大气层,A点需随地球转动到B时才能观察到日出,(破题关键)由几何关系,∠AOB=(90°-β)-(90°-α)=16°,故提前的时间为t=T≈5.3 s,选项B正确。
4.答案 (1)1.6 (2)53° (3)
解析 (1)AC界面上,由几何关系可知入射角为i=53°
折射角为γ=30°
则折射率为n=
解得n=1.6
(2)在F点,入射角为i'=60°
可知sin i'>
即在F点发生全反射(破题关键),光线在AC面的入射角为i″=30°
在AC面发生折射,由n=
解得θ=53°
(3)光束在玻璃中的传播速度为v=
由几何关系可知,光束在玻璃中的路程为d=L+L+L=2L
解得光束在玻璃中传播时间为t===
5.答案 (1) (2)(6-) m
解析 (1)根据题意可得,最低可以观察位置的光路图如图所示
根据几何关系有∠PAB=∠AOD
由于PB=AD=3 m
则OD=AB=4 m
QO=QD-OD=7 m-4 m=3 m
则有sin β==,sin α==
根据折射定律可得,海水的折射率为n==
(2)若涨潮时海面CD上升至与海岸AB平齐,潜水员仍处于海面下E点,此时最低可以观察位置的光路图如图所示
设HB等于x,由几何知识有sin i=
sin r=
根据折射定律有n==
联立解得x= m
则此时能看到的标尺杆长度为l=(6-) m
6.答案 (1)4 cm (2) cm2
关键点拨 (1)若沿SC'的光线恰好发生全反射,则右侧面恰好均有光射出。
(2)若光线在左侧面的M点刚好发生全反射,则以A点为圆心、AM为半径,在ADD'A'面内的圆弧内均有光线射出。
解析 (1)当右侧面恰好全部都有光线射出时,C'点恰好发生全反射,
此时C'点的入射角记为θ,有sin θ==
可得tan θ=
在△SBC'中tan θ=
得SB===4 cm
(2)由(1)中的结论可得AS=AB-SB=2 cm
设光线在左侧面的M点刚好发生全反射(解题技法),M点到A点的距离为r,则有
tan θ=
解得r= cm
则以A点为圆心、AM为半径,在ADD'A'面内的圆弧内均有光线射出,故左侧面有光线射出的面积为S=πr2= cm2
7.答案 (1)30° (2) (3)
解析 (1)从P点发出的光入射到大气层外表面处时,发生全反射的临界角C满足sin C=,
解得C=30°
(2)当P点发出的光线在大气层外表面恰好发生全反射时,光路如图所示。
由正弦定理可得=,解得α=135°
故从P点射出的光线在大气层外表面恰好发生全反射时,光线PB与OP延长线的夹角为45°,大气层外表面发光区域在截面上对应的圆心角为
β=2×(45°-C)=30°
故发光区域在截面上形成的弧长为
l=×2π×r=
(3)如图所示,临界光线从B点射向卫星轨道上的C点,在直角△OBC中,由几何关系可得
cos ∠BOC==,解得∠BOC=15°
即轨道上能观测到光的部分对应的圆心角为60°,对应的轨道弧长为l'=×2π×=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
