5.3 简单的轴对称图形(1)课件(共29张PPT)北师大版数学七年级下册
文档属性
| 名称 | 5.3 简单的轴对称图形(1)课件(共29张PPT)北师大版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
简单的轴对称图形
单击此处添加副标题
问题1:关于轴对称,我们研究了哪些内容?
定义
性质
全等图形
定义
应用
全等三角形
判定
特例:
性质
定义
性质
问题2:类比三角形的研究路径,你认为我们还可以研究轴对称图形的哪些内容?
定义
性质
特例
回顾思考
目录
03
问题3:对于这一课题,你会想到哪些图形?
06
角
04
等腰三角形
07
简单的轴对称图形
05
线段
A
B
C
顶角
底角
底角
腰
腰
底边
有两边相等的三角形叫做等腰三角形.等腰三角形中相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
等腰三角形
A
B
C
请你拿出课前准备好的等腰三角形纸片,试着找出等腰三角形的对称轴.
操作探究
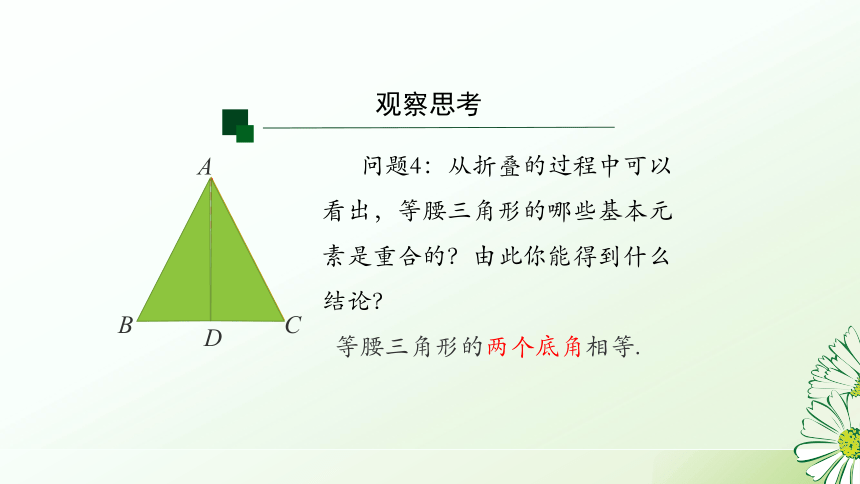
问题4:从折叠的过程中可以看出,等腰三角形的哪些基本元素是重合的?由此你能得到什么结论?
A
B
C
D
等腰三角形的两个底角相等.
观察思考
问题5:关于折痕,你还能提出哪些问题?
观察思考
A
B
C
D
(1)折痕是顶角的平分线吗?
(2)折痕是底边上的中线吗?
(3)折痕是底边上的高吗?
重合元素 等量关系 AD
重合的边
重合的角
∠BAD=∠CAD
∠BDA=∠CDA
∠B=∠C
AB=AC
BD=CD
AD=AD
底边上的中线
底边上的高
顶角的平分线
A
B
C
D
性质1:等腰三角形是轴对称图形.
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ), 它们所在的直线都是等腰三角形的对称轴.
性质3: 等腰三角形的两个底角相等.
等腰三角形的性质
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ).
A
B
C
D
符号语言:如图, 在△ABC中,
因为AB=AC, ∠BAD=∠CAD(已知),
所以BD=CD, AD⊥BC(三线合一)
等腰三角形的性质
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ).
A
B
C
D
符号语言:如图, 在△ABC中,
等腰三角形的性质
因为AB=AC, BD=CD (已知),
所以∠BAD=∠CAD, AD⊥BC(三线合一)
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ).
A
B
C
D
符号语言:如图, 在△ABC中,
等腰三角形的性质
因为AB=AC, AD⊥BC(已知),
所以BD=CD, ∠BAD=∠CAD(三线合一)
符号语言:如图, 在△ABC中,
因为 AB=AC,
所以 ∠B=∠C.
性质3: 等腰三角形的两个底角相等.
A
B
C
D
等腰三角形的性质
问题6:等腰三角形的性质有什么作用?
提供了证明角相等、线段相等、线段垂直的方法.
等腰三角形的性质
问题7:等边三角形有几条对称轴?你能发现它的哪些特征?
有3条对称轴
三个内角相等
具有“三线合一”性质
等边三角形的性质
你有哪些办法可以得到一个等腰三角形? 与同伴交流.
A
B
C
AB=AC
等腰三角形
你能尝试用圆规吗?
1. 在△ABC 中,AB = AC.
(1)若∠A = 40°,则∠C =______.
(2)若∠B = 72°,则∠A =______.
(3)若三角形一个内角是50°,
则∠B =____________.
A
B
C
70°
36°
50°或 65°
例题讲解
50°
顶角
底角
∠B=50°
∠B=65°
1. 在△ABC 中,AB = AC.
(1)若∠A = 40°,则∠C =______.
(2)若∠B = 72°,则∠A =______.
(3)若三角形一个内角是50°,
则∠B =____________.
A
B
C
知识点:①三角形内角和;②等腰三角形的两个底角相等
数学思想:分类讨论
70°
36°
50°或 65°
例题讲解
变式:若等腰△ABC 中一个内角是50°,则∠B = __________________.
50°
顶角
底角
∠B是顶角
∠B是顶角
∠B是底角
∠B是底角
∠B=50°
∠B=65°
∠B=80°
∠B=50°
例题讲解
50°或 65°或 80°
2. 如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5
C.4 D.3
B
例题讲解
A
B
C
D
1.(1)等腰三角形一个底角为75°,它的另外两个角为_________;
(2)等腰三角形一个角为70°,它的另外两个角为___________________;
(3)等腰三角形一个角为110°,它的另外两个角为__________.
75°, 30°
70°,40°或55°,55°
35°,35°
随堂练习
2. 墙上钉了一根木条,小明想检验这根木条是否水平,他拿来一个如图所示的测平仪。在这个测平仪中AB=AC,BC边的中点D处挂了一个重锤。小明将BC边与木条重合,观察此时重锤是否通过A点,如果重锤过A点,那么这根木条就是水平的,你能说明其中的道理吗?
随堂练习
(整体性)性质1:等腰三角形是轴对称图形.
(相关要素)性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ), 它们所在的直线都是等腰三角形的对称轴.
(基本要素)性质3: 等腰三角形的两个底角相等.
课堂小结:知识内容
分类讨论:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
课堂小结:思想方法
说明线段相等的方法:全等三角形、三线合一.
研究路径:定义—性质—特例(等腰三角形).
研究方法:①实验、观察、归纳;
②图形变换:轴对称的角度.
研究内容:等腰三角形的基本要素(边、角)、
相关要素(高线、中线、角平分线).
课堂小结:研究路径
简单的轴对称图形
单击此处添加副标题
问题1:关于轴对称,我们研究了哪些内容?
定义
性质
全等图形
定义
应用
全等三角形
判定
特例:
性质
定义
性质
问题2:类比三角形的研究路径,你认为我们还可以研究轴对称图形的哪些内容?
定义
性质
特例
回顾思考
目录
03
问题3:对于这一课题,你会想到哪些图形?
06
角
04
等腰三角形
07
简单的轴对称图形
05
线段
A
B
C
顶角
底角
底角
腰
腰
底边
有两边相等的三角形叫做等腰三角形.等腰三角形中相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
等腰三角形
A
B
C
请你拿出课前准备好的等腰三角形纸片,试着找出等腰三角形的对称轴.
操作探究
问题4:从折叠的过程中可以看出,等腰三角形的哪些基本元素是重合的?由此你能得到什么结论?
A
B
C
D
等腰三角形的两个底角相等.
观察思考
问题5:关于折痕,你还能提出哪些问题?
观察思考
A
B
C
D
(1)折痕是顶角的平分线吗?
(2)折痕是底边上的中线吗?
(3)折痕是底边上的高吗?
重合元素 等量关系 AD
重合的边
重合的角
∠BAD=∠CAD
∠BDA=∠CDA
∠B=∠C
AB=AC
BD=CD
AD=AD
底边上的中线
底边上的高
顶角的平分线
A
B
C
D
性质1:等腰三角形是轴对称图形.
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ), 它们所在的直线都是等腰三角形的对称轴.
性质3: 等腰三角形的两个底角相等.
等腰三角形的性质
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ).
A
B
C
D
符号语言:如图, 在△ABC中,
因为AB=AC, ∠BAD=∠CAD(已知),
所以BD=CD, AD⊥BC(三线合一)
等腰三角形的性质
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ).
A
B
C
D
符号语言:如图, 在△ABC中,
等腰三角形的性质
因为AB=AC, BD=CD (已知),
所以∠BAD=∠CAD, AD⊥BC(三线合一)
性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ).
A
B
C
D
符号语言:如图, 在△ABC中,
等腰三角形的性质
因为AB=AC, AD⊥BC(已知),
所以BD=CD, ∠BAD=∠CAD(三线合一)
符号语言:如图, 在△ABC中,
因为 AB=AC,
所以 ∠B=∠C.
性质3: 等腰三角形的两个底角相等.
A
B
C
D
等腰三角形的性质
问题6:等腰三角形的性质有什么作用?
提供了证明角相等、线段相等、线段垂直的方法.
等腰三角形的性质
问题7:等边三角形有几条对称轴?你能发现它的哪些特征?
有3条对称轴
三个内角相等
具有“三线合一”性质
等边三角形的性质
你有哪些办法可以得到一个等腰三角形? 与同伴交流.
A
B
C
AB=AC
等腰三角形
你能尝试用圆规吗?
1. 在△ABC 中,AB = AC.
(1)若∠A = 40°,则∠C =______.
(2)若∠B = 72°,则∠A =______.
(3)若三角形一个内角是50°,
则∠B =____________.
A
B
C
70°
36°
50°或 65°
例题讲解
50°
顶角
底角
∠B=50°
∠B=65°
1. 在△ABC 中,AB = AC.
(1)若∠A = 40°,则∠C =______.
(2)若∠B = 72°,则∠A =______.
(3)若三角形一个内角是50°,
则∠B =____________.
A
B
C
知识点:①三角形内角和;②等腰三角形的两个底角相等
数学思想:分类讨论
70°
36°
50°或 65°
例题讲解
变式:若等腰△ABC 中一个内角是50°,则∠B = __________________.
50°
顶角
底角
∠B是顶角
∠B是顶角
∠B是底角
∠B是底角
∠B=50°
∠B=65°
∠B=80°
∠B=50°
例题讲解
50°或 65°或 80°
2. 如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5
C.4 D.3
B
例题讲解
A
B
C
D
1.(1)等腰三角形一个底角为75°,它的另外两个角为_________;
(2)等腰三角形一个角为70°,它的另外两个角为___________________;
(3)等腰三角形一个角为110°,它的另外两个角为__________.
75°, 30°
70°,40°或55°,55°
35°,35°
随堂练习
2. 墙上钉了一根木条,小明想检验这根木条是否水平,他拿来一个如图所示的测平仪。在这个测平仪中AB=AC,BC边的中点D处挂了一个重锤。小明将BC边与木条重合,观察此时重锤是否通过A点,如果重锤过A点,那么这根木条就是水平的,你能说明其中的道理吗?
随堂练习
(整体性)性质1:等腰三角形是轴对称图形.
(相关要素)性质2:等腰三角形顶角的平分线、 底边上的中线、 底边上的高重合(也称 “三线合一” ), 它们所在的直线都是等腰三角形的对称轴.
(基本要素)性质3: 等腰三角形的两个底角相等.
课堂小结:知识内容
分类讨论:等腰三角形的两个底角相等,已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
课堂小结:思想方法
说明线段相等的方法:全等三角形、三线合一.
研究路径:定义—性质—特例(等腰三角形).
研究方法:①实验、观察、归纳;
②图形变换:轴对称的角度.
研究内容:等腰三角形的基本要素(边、角)、
相关要素(高线、中线、角平分线).
课堂小结:研究路径
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
