第三单元 长方体和正方体 (单元测试)-2023-2024学年五年级下册数学人教版(含解析)
文档属性
| 名称 | 第三单元 长方体和正方体 (单元测试)-2023-2024学年五年级下册数学人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 263.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 15:58:27 | ||
图片预览




文档简介
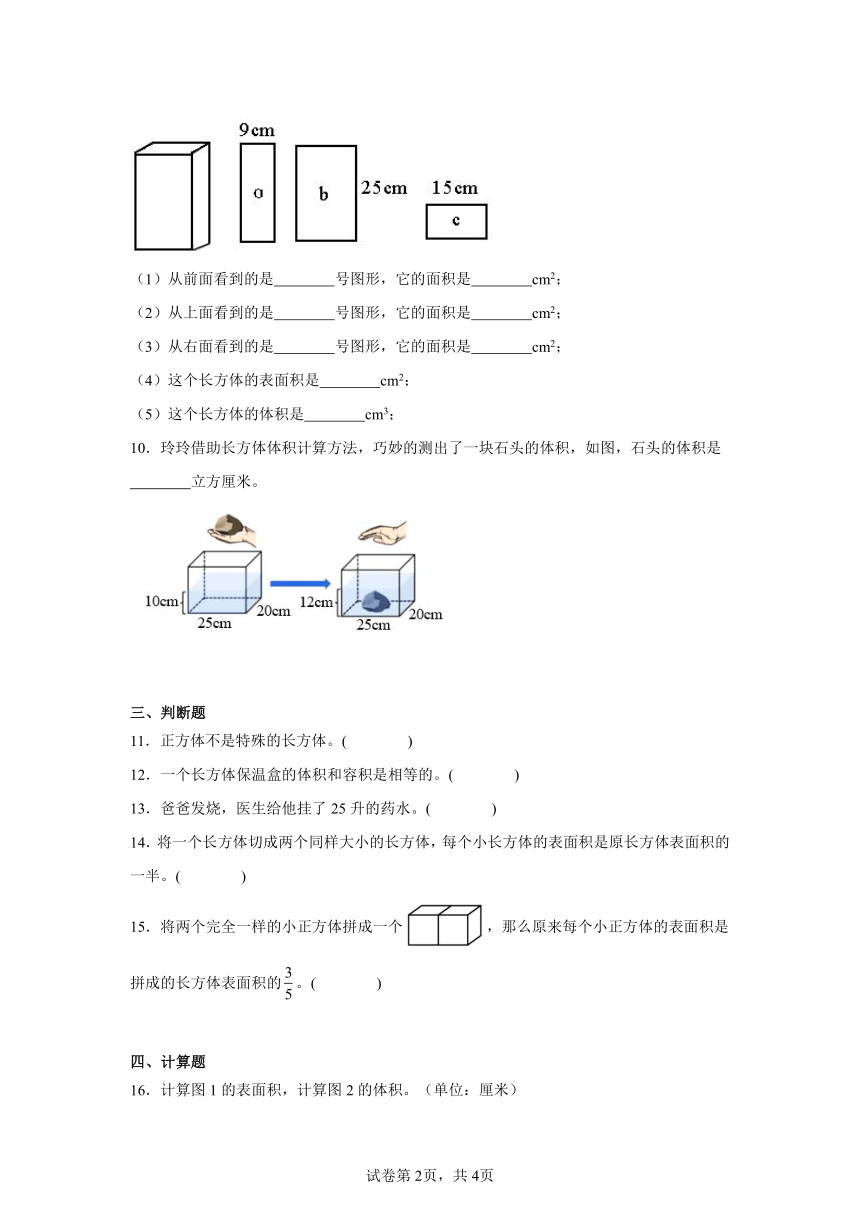
第三单元 长方体和正方体(单元测试)
一、选择题
1.如图是一个长方体物品的长、宽、高,请你根据具体数据估计这可能是( )。
A.书包 B.文具盒 C.数学书 D.粉笔盒
2.一个长方体油桶最多容纳64升油,从里面量,油桶长8分米,宽4分米,高( )分米。
A.25 B.2.5 C.2
3.正方体的棱长扩大到原来的3倍,那么它的体积( )。
A.扩大到原来的9倍 B.不变 C.扩大到原来的27倍
4.用一根长( )的铁丝正好可以做一个长6厘米,宽5厘米,高3厘米的长方体框架。
A.28厘米 B.56厘米 C.126平方厘米 D.90立方厘米
5.下面四个图形中,每个小正方形都标上了颜色,若要求一个正方体两个相对面上的颜色都一样,那么不可能是这个正方体展开图的是( )。
A. B. C. D.
二、填空题
6.一本小学数学课本的形状是 ,它有 面, 条棱.
7.一个正方体棱长总和是60cm,每一条棱长是 cm,它的表面积是 cm2,体积是 cm3。
8.观察下图。小球和珊瑚相比,体积较大的是 。
9.有一个长方体,如下左图,从不同的角度看到图、b、c.
(1)从前面看到的是 号图形,它的面积是 cm2;
(2)从上面看到的是 号图形,它的面积是 cm2;
(3)从右面看到的是 号图形,它的面积是 cm2;
(4)这个长方体的表面积是 cm2;
(5)这个长方体的体积是 cm3;
10.玲玲借助长方体体积计算方法,巧妙的测出了一块石头的体积,如图,石头的体积是
立方厘米。
三、判断题
11.正方体不是特殊的长方体。( )
12.一个长方体保温盒的体积和容积是相等的。( )
13.爸爸发烧,医生给他挂了25升的药水。( )
14.将一个长方体切成两个同样大小的长方体,每个小长方体的表面积是原长方体表面积的一半。( )
15.将两个完全一样的小正方体拼成一个,那么原来每个小正方体的表面积是拼成的长方体表面积的。( )
四、计算题
16.计算图1的表面积,计算图2的体积。(单位:厘米)
五、解答题
17.一个正方体茶叶包装盒,棱长为15厘米,制作这样的包装盒8个需要多少平方分米的铁盒?(接口处忽略不计)
18.一个长方体玻璃容器,从里面量长、宽均为2分米,向容器中倒入一些水,再把一个铁制品完全浸没在水中。这时量得容器内的水的高度增加了5厘米。这个铁制品的体积是多少?
19.育才实验小学要建一个长60米,宽50米的长方形足球场,先要铺6厘米厚的煤渣,再铺12厘米厚的三合土。一共需要煤渣和三合土多少立方米?
20.将一块不规则的石块全部浸没在长8分米,宽5分米装有水的长方体容器里,测得水面升高5厘米。这块石块的体积是多少?
21.一根方钢,长6米,横截面是一个边长为4厘米的正方形。
(1)这根方钢重多少千克?(1立方厘米钢重0.01千克)
(2)一辆载重5000千克的货车能否一次运载50根这样的方钢?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据生活经验、数据大小及对长度单位的认识,结合长方体的特征可知,书包、数学书、粉笔盒不可能是长25cm,宽10cm,高4cm的长方体,据此选择。
【详解】A.书包的高超过4cm,所以这个物品不可能是书包;
B.文具盒的长约是25cm,宽约是10cm,高约是4cm,所以这个物品可能是文具盒;
C.数学书的高小于4cm,所以这个物品不可能是数学书;
D.粉笔盒的长小于25cm,高大于4cm,所以这个物品不可能是粉笔盒。
故答案为:B
【点睛】本题考查长方体的特征以及根据计量单位和数据的大小,选择合适的物体。
2.C
【分析】长方体的体积=长×宽×高,则长方体的高=长方体的体积÷长÷宽,把题中数据代入公式计算即可。
【详解】64升=64立方分米
64÷8÷4
=8÷4
=2(分米)
故答案为:C
【点睛】熟练运用长方体的体积计算公式是解答题目的关键。
3.C
【分析】根据正方体的体积公式:V=a3以及因数与积的变化规律,三个因数都扩大到原来的3倍,积就扩大到原来的3×3×3=27倍;由此解答即可。
【详解】根据分析得,3×3×3=27。
即正方体的棱长扩大3倍,那么它的体积扩大到原来的27倍。
故答案为:C
【点睛】此题主要根据正方体的体积计算方法和因数与积的变化规律解决问题。
4.B
【分析】根据长方体棱长总和=(长+宽+高)×4,列式计算即可。
【详解】(6+5+3)×4
=14×4
=56(厘米)
故答案为:B
【点睛】关键是熟悉长方体特征,掌握长方体棱长总和公式。
5.C
【分析】根据学习的展开和折叠,正方形的展开图分四种,11种展开的常见形式解答。
【详解】A.属于正方体展开图的“2-2-2”结构,折叠正方体后红与红相对,绿与绿相对,黄与黄相对;
B.属于正方体展开图的“1-4-1”结构,折叠正方体后,红与红相对,绿与绿相对,黄与黄相对;
C.属于正方形展开图的“1-4-1”结构,折叠正方体后,其中红与绿相对,黄与黄相对,不符合题意;
D.属于正方体展开图的“1-4-1”结构,折叠正方体后,红与红相对,绿与绿相对,黄与黄相对。
故答案选:C
【点睛】本题考查正方体的展开与折叠,根据展开图的类型解答问题。
6. 长方体 6 12
【详解】解:一本小学数学课本的形状是长方体,它有6个面,12条棱. 故答案为长方体,6,12.
根据长方体的特征,长方体有12条棱,6个面,8个顶点.一本小学数学课本的形状是长方体.由此解答.
7. 5 150 125
【分析】根据正方体的棱长总和=棱长×12,代入数据用60除以12求出正方体的棱长,再利用正方体的表面积公式:S=6a2和正方体的体积公式:V=a3,代入数据即可求正方体的表面积和体积。
【详解】60÷12=5(cm)
6×5×5=150(cm2)
5×5×5=125(cm3)
【点睛】此题的解题关键是灵活运用正方体的棱长总和公式求出棱长,再根据正方体的表面积和体积公式求出最终的结果。
8.珊瑚
【分析】根据小球和珊瑚放进水槽中水面上升的高度来比较体积大小即可。
【详解】小球放入水中,水面上升:9.5-8=1.5
珊瑚放进水中,水面上升:12-9.5=2.5
2.5>1.5
所以珊瑚的体积大。
【点睛】本题考查体积的概念,解答本题的关键是掌握物体所占空间的大小叫做物体的体积,根据水面上升的高度来比较小球和珊瑚的体积大小。
9. (1)b 375 (2) c 135 (3)a 225 (4)1470 (5)3375
【分析】观察这个长方体和每个面的形状,确定a是左右面、b是前后面、c是上下面;长方体的长是15cm,宽是9cm,高是25cm.根据每个面的长和宽计算出每个面的面积;把所有面的面积相加就是长方体的表面积;根据长方体体积公式计算体积即可.
【详解】(1)从前面看到的是b号图形,它的面积是25×15=375(cm );
(2)从上面看到的是c号图形,它的面积是15×9=135(cm );
(3)从右面看到的是a号图形,它的面积是25×9=225(cm );
(4)表面积(375+135+225)×2
=735×2
=1470(cm );
(5)体积:15×25×9=3375(cm ).
故答案为(1)b;375;(2)c;135;(3)a;225;(4)1470;(5)3375.
10.1000
【分析】根据题意,把石头放到容器中,水上升了(12-10)厘米,石头的体积等于水面上升的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【详解】25×20×(12-10)
=500×2
=1000(立方厘米)
即石头的体积是1000立方厘米。
【点睛】此题考查的目的是理解掌握不规则物体的体积的计算方法利用排水法,根据长方体的体积公式解答。
11.×
【详解】根据正方体的特征,长、宽、高都相等的长方体叫做正方体,正方体是特殊的长方体。所以原题干说法错误。
故答案为:×
12.×
【分析】根据体积、容积的意义,物体所占空间的大小叫做物体的体积,所能容纳物体的体积叫做物体的容积。计算物体的体积的方法与计算物体容积的方法相同,但计算体积时是从物体外面进行测量;计算容积时是从物体的里面就那些测量,一个容器壁再薄也有厚度,因此,一个物体的容积要小于它的体积。
【详解】根据物体体积、容积的意义,一个容器的体积一定大于它的容积,所以原题中“一个长方体保温盒的体积和容积是相等的”说法错误。
故答案为:×
【点睛】本题考查物体的体积和容积,明确体积和容积的意义是解答本题的关键。
13.×
【分析】根据生活实际可知,一大瓶饮料大约是1升,25升的药水相当于25大瓶饮料,依此判断即可。
【详解】根据分析可知:爸爸发烧,医生不可能给他挂25升的药水。
故答案为:×
【点睛】此题考查的是对升的认识,应熟练掌握1升的实际大小。
14.×
【分析】将长方体切成两个完全相同的小长方体后,两个小长方体的表面积和比原来长方体的表面积增加了两个切开面的面积,由此即可进行判断。
【详解】将一个长方体切成两个同样大小的长方体,增加了两个横截面的面积,即每个小长方体的表面积比原长方体表面积的一半多一个切开面的面积。
故答案为:×
【点睛】此题的解题关键是熟悉长方体的特征以及长方体切拼后面积的变化。
15.√
【分析】根据正方体表面积S=6a2,长方体表面积S=(ab+ah+bh)×2,分别求出它们的表面积,即可解答。
【详解】设小正方体棱长为a,则长方体的长宽高分别是2a、a、a。
小正方体表面积=a×a×6=6a2
长方体表面积=(2a×a+2a×a+a×a)×2=10a2
6a2÷10a2=
因此,原来每个小正方体的表面积是拼成的长方体表面积的。
故答案为:√
【点睛】本题考查的是正方体、长方体表面积公式的灵活运用。
16.150平方厘米;109立方厘米
【分析】图1的表面积=完整的长方体表面积+正方体4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;图2的体积=正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【详解】(8×3+8×3+3×3)×2+3×3×4
=(24+24+9)×2+36
=57×2+36
=114+36
=150(平方厘米)
5×5×5-4×2×2
=125-16
=109(立方厘米)
17.108平方分米
【分析】根据正方体的表面积公式:V=6a2,代入棱长的数据,求出制作一个茶叶包装盒需要的铁盒面积,再乘8,即可求出制作8个包装盒需要的铁盒面积。
【详解】6×15×15×8
=90×15×8
=10800(平方厘米)
10800平方厘米=108平方分米
答:制作这样的包装盒8个需要108平方分米的铁盒。
【点睛】此题的解题关键是熟悉正方体的表面积计算公式,注意换算单位。
18.2000立方厘米
【分析】这个铁制品的体积就是浸入水中后水面升高的水体积,根据长方体的体积=长×宽×高,代入数据,解答即可。
【详解】2分米=20厘米
20×20×5
=400×5
=2000(立方厘米)
答:这个铁制品的体积是2000立方厘米。
19.540立方米
【分析】先求出煤渣和三合土的高度和;再根据“长方体的体积=长×宽×高”求出煤渣和三合土的体积和。
【详解】6+12=18(厘米)
18厘米=0.18米
60×50×0.18
=3000×0.18
=540(立方米)
答:一共需要煤渣和三合土540立方米。
【点睛】计算长方体的体积时,要注意长、宽、高的单位是否统一。
20.20立方分米
【分析】石块完全浸没在水里后,石块的体积=水面上升的体积,水面上升的体积可看作长为8分米,宽为5分米,高为5厘米的长方体的体积,先统一单位后,再根据长方体的体积公式,把数据代入即可得解。
【详解】5厘米=0.5分米
8×5×0.5
=40×0.5
=20(立方分米)
答:这块石块的体积是20立方分米。
【点睛】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式,解决问题。
21.(1)96千克;
(2)能
【分析】(1)方钢的体积=方钢的横截面积×方钢的长,方钢的重量=方钢的体积×每立方厘米方钢的重量;
(2)用乘法计算出50根方钢的重量,最后和货车载重量比较大小;据此解答。
【详解】(1)6米=600厘米
4×4×600×0.01
=16×600×0.01
=9600×0.01
=96(千克)
答:这根方钢重96千克
(2)96×50=4800(千克)
因为5000千克>4800千克,所以一辆载重5000千克的货车能一次运载50根这样的方钢。
答:一辆载重5000千克的货车能一次运载50根这样的方钢。
【点睛】根据长方体体积的计算方法求出每根方钢的体积是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.如图是一个长方体物品的长、宽、高,请你根据具体数据估计这可能是( )。
A.书包 B.文具盒 C.数学书 D.粉笔盒
2.一个长方体油桶最多容纳64升油,从里面量,油桶长8分米,宽4分米,高( )分米。
A.25 B.2.5 C.2
3.正方体的棱长扩大到原来的3倍,那么它的体积( )。
A.扩大到原来的9倍 B.不变 C.扩大到原来的27倍
4.用一根长( )的铁丝正好可以做一个长6厘米,宽5厘米,高3厘米的长方体框架。
A.28厘米 B.56厘米 C.126平方厘米 D.90立方厘米
5.下面四个图形中,每个小正方形都标上了颜色,若要求一个正方体两个相对面上的颜色都一样,那么不可能是这个正方体展开图的是( )。
A. B. C. D.
二、填空题
6.一本小学数学课本的形状是 ,它有 面, 条棱.
7.一个正方体棱长总和是60cm,每一条棱长是 cm,它的表面积是 cm2,体积是 cm3。
8.观察下图。小球和珊瑚相比,体积较大的是 。
9.有一个长方体,如下左图,从不同的角度看到图、b、c.
(1)从前面看到的是 号图形,它的面积是 cm2;
(2)从上面看到的是 号图形,它的面积是 cm2;
(3)从右面看到的是 号图形,它的面积是 cm2;
(4)这个长方体的表面积是 cm2;
(5)这个长方体的体积是 cm3;
10.玲玲借助长方体体积计算方法,巧妙的测出了一块石头的体积,如图,石头的体积是
立方厘米。
三、判断题
11.正方体不是特殊的长方体。( )
12.一个长方体保温盒的体积和容积是相等的。( )
13.爸爸发烧,医生给他挂了25升的药水。( )
14.将一个长方体切成两个同样大小的长方体,每个小长方体的表面积是原长方体表面积的一半。( )
15.将两个完全一样的小正方体拼成一个,那么原来每个小正方体的表面积是拼成的长方体表面积的。( )
四、计算题
16.计算图1的表面积,计算图2的体积。(单位:厘米)
五、解答题
17.一个正方体茶叶包装盒,棱长为15厘米,制作这样的包装盒8个需要多少平方分米的铁盒?(接口处忽略不计)
18.一个长方体玻璃容器,从里面量长、宽均为2分米,向容器中倒入一些水,再把一个铁制品完全浸没在水中。这时量得容器内的水的高度增加了5厘米。这个铁制品的体积是多少?
19.育才实验小学要建一个长60米,宽50米的长方形足球场,先要铺6厘米厚的煤渣,再铺12厘米厚的三合土。一共需要煤渣和三合土多少立方米?
20.将一块不规则的石块全部浸没在长8分米,宽5分米装有水的长方体容器里,测得水面升高5厘米。这块石块的体积是多少?
21.一根方钢,长6米,横截面是一个边长为4厘米的正方形。
(1)这根方钢重多少千克?(1立方厘米钢重0.01千克)
(2)一辆载重5000千克的货车能否一次运载50根这样的方钢?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据生活经验、数据大小及对长度单位的认识,结合长方体的特征可知,书包、数学书、粉笔盒不可能是长25cm,宽10cm,高4cm的长方体,据此选择。
【详解】A.书包的高超过4cm,所以这个物品不可能是书包;
B.文具盒的长约是25cm,宽约是10cm,高约是4cm,所以这个物品可能是文具盒;
C.数学书的高小于4cm,所以这个物品不可能是数学书;
D.粉笔盒的长小于25cm,高大于4cm,所以这个物品不可能是粉笔盒。
故答案为:B
【点睛】本题考查长方体的特征以及根据计量单位和数据的大小,选择合适的物体。
2.C
【分析】长方体的体积=长×宽×高,则长方体的高=长方体的体积÷长÷宽,把题中数据代入公式计算即可。
【详解】64升=64立方分米
64÷8÷4
=8÷4
=2(分米)
故答案为:C
【点睛】熟练运用长方体的体积计算公式是解答题目的关键。
3.C
【分析】根据正方体的体积公式:V=a3以及因数与积的变化规律,三个因数都扩大到原来的3倍,积就扩大到原来的3×3×3=27倍;由此解答即可。
【详解】根据分析得,3×3×3=27。
即正方体的棱长扩大3倍,那么它的体积扩大到原来的27倍。
故答案为:C
【点睛】此题主要根据正方体的体积计算方法和因数与积的变化规律解决问题。
4.B
【分析】根据长方体棱长总和=(长+宽+高)×4,列式计算即可。
【详解】(6+5+3)×4
=14×4
=56(厘米)
故答案为:B
【点睛】关键是熟悉长方体特征,掌握长方体棱长总和公式。
5.C
【分析】根据学习的展开和折叠,正方形的展开图分四种,11种展开的常见形式解答。
【详解】A.属于正方体展开图的“2-2-2”结构,折叠正方体后红与红相对,绿与绿相对,黄与黄相对;
B.属于正方体展开图的“1-4-1”结构,折叠正方体后,红与红相对,绿与绿相对,黄与黄相对;
C.属于正方形展开图的“1-4-1”结构,折叠正方体后,其中红与绿相对,黄与黄相对,不符合题意;
D.属于正方体展开图的“1-4-1”结构,折叠正方体后,红与红相对,绿与绿相对,黄与黄相对。
故答案选:C
【点睛】本题考查正方体的展开与折叠,根据展开图的类型解答问题。
6. 长方体 6 12
【详解】解:一本小学数学课本的形状是长方体,它有6个面,12条棱. 故答案为长方体,6,12.
根据长方体的特征,长方体有12条棱,6个面,8个顶点.一本小学数学课本的形状是长方体.由此解答.
7. 5 150 125
【分析】根据正方体的棱长总和=棱长×12,代入数据用60除以12求出正方体的棱长,再利用正方体的表面积公式:S=6a2和正方体的体积公式:V=a3,代入数据即可求正方体的表面积和体积。
【详解】60÷12=5(cm)
6×5×5=150(cm2)
5×5×5=125(cm3)
【点睛】此题的解题关键是灵活运用正方体的棱长总和公式求出棱长,再根据正方体的表面积和体积公式求出最终的结果。
8.珊瑚
【分析】根据小球和珊瑚放进水槽中水面上升的高度来比较体积大小即可。
【详解】小球放入水中,水面上升:9.5-8=1.5
珊瑚放进水中,水面上升:12-9.5=2.5
2.5>1.5
所以珊瑚的体积大。
【点睛】本题考查体积的概念,解答本题的关键是掌握物体所占空间的大小叫做物体的体积,根据水面上升的高度来比较小球和珊瑚的体积大小。
9. (1)b 375 (2) c 135 (3)a 225 (4)1470 (5)3375
【分析】观察这个长方体和每个面的形状,确定a是左右面、b是前后面、c是上下面;长方体的长是15cm,宽是9cm,高是25cm.根据每个面的长和宽计算出每个面的面积;把所有面的面积相加就是长方体的表面积;根据长方体体积公式计算体积即可.
【详解】(1)从前面看到的是b号图形,它的面积是25×15=375(cm );
(2)从上面看到的是c号图形,它的面积是15×9=135(cm );
(3)从右面看到的是a号图形,它的面积是25×9=225(cm );
(4)表面积(375+135+225)×2
=735×2
=1470(cm );
(5)体积:15×25×9=3375(cm ).
故答案为(1)b;375;(2)c;135;(3)a;225;(4)1470;(5)3375.
10.1000
【分析】根据题意,把石头放到容器中,水上升了(12-10)厘米,石头的体积等于水面上升的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【详解】25×20×(12-10)
=500×2
=1000(立方厘米)
即石头的体积是1000立方厘米。
【点睛】此题考查的目的是理解掌握不规则物体的体积的计算方法利用排水法,根据长方体的体积公式解答。
11.×
【详解】根据正方体的特征,长、宽、高都相等的长方体叫做正方体,正方体是特殊的长方体。所以原题干说法错误。
故答案为:×
12.×
【分析】根据体积、容积的意义,物体所占空间的大小叫做物体的体积,所能容纳物体的体积叫做物体的容积。计算物体的体积的方法与计算物体容积的方法相同,但计算体积时是从物体外面进行测量;计算容积时是从物体的里面就那些测量,一个容器壁再薄也有厚度,因此,一个物体的容积要小于它的体积。
【详解】根据物体体积、容积的意义,一个容器的体积一定大于它的容积,所以原题中“一个长方体保温盒的体积和容积是相等的”说法错误。
故答案为:×
【点睛】本题考查物体的体积和容积,明确体积和容积的意义是解答本题的关键。
13.×
【分析】根据生活实际可知,一大瓶饮料大约是1升,25升的药水相当于25大瓶饮料,依此判断即可。
【详解】根据分析可知:爸爸发烧,医生不可能给他挂25升的药水。
故答案为:×
【点睛】此题考查的是对升的认识,应熟练掌握1升的实际大小。
14.×
【分析】将长方体切成两个完全相同的小长方体后,两个小长方体的表面积和比原来长方体的表面积增加了两个切开面的面积,由此即可进行判断。
【详解】将一个长方体切成两个同样大小的长方体,增加了两个横截面的面积,即每个小长方体的表面积比原长方体表面积的一半多一个切开面的面积。
故答案为:×
【点睛】此题的解题关键是熟悉长方体的特征以及长方体切拼后面积的变化。
15.√
【分析】根据正方体表面积S=6a2,长方体表面积S=(ab+ah+bh)×2,分别求出它们的表面积,即可解答。
【详解】设小正方体棱长为a,则长方体的长宽高分别是2a、a、a。
小正方体表面积=a×a×6=6a2
长方体表面积=(2a×a+2a×a+a×a)×2=10a2
6a2÷10a2=
因此,原来每个小正方体的表面积是拼成的长方体表面积的。
故答案为:√
【点睛】本题考查的是正方体、长方体表面积公式的灵活运用。
16.150平方厘米;109立方厘米
【分析】图1的表面积=完整的长方体表面积+正方体4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;图2的体积=正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【详解】(8×3+8×3+3×3)×2+3×3×4
=(24+24+9)×2+36
=57×2+36
=114+36
=150(平方厘米)
5×5×5-4×2×2
=125-16
=109(立方厘米)
17.108平方分米
【分析】根据正方体的表面积公式:V=6a2,代入棱长的数据,求出制作一个茶叶包装盒需要的铁盒面积,再乘8,即可求出制作8个包装盒需要的铁盒面积。
【详解】6×15×15×8
=90×15×8
=10800(平方厘米)
10800平方厘米=108平方分米
答:制作这样的包装盒8个需要108平方分米的铁盒。
【点睛】此题的解题关键是熟悉正方体的表面积计算公式,注意换算单位。
18.2000立方厘米
【分析】这个铁制品的体积就是浸入水中后水面升高的水体积,根据长方体的体积=长×宽×高,代入数据,解答即可。
【详解】2分米=20厘米
20×20×5
=400×5
=2000(立方厘米)
答:这个铁制品的体积是2000立方厘米。
19.540立方米
【分析】先求出煤渣和三合土的高度和;再根据“长方体的体积=长×宽×高”求出煤渣和三合土的体积和。
【详解】6+12=18(厘米)
18厘米=0.18米
60×50×0.18
=3000×0.18
=540(立方米)
答:一共需要煤渣和三合土540立方米。
【点睛】计算长方体的体积时,要注意长、宽、高的单位是否统一。
20.20立方分米
【分析】石块完全浸没在水里后,石块的体积=水面上升的体积,水面上升的体积可看作长为8分米,宽为5分米,高为5厘米的长方体的体积,先统一单位后,再根据长方体的体积公式,把数据代入即可得解。
【详解】5厘米=0.5分米
8×5×0.5
=40×0.5
=20(立方分米)
答:这块石块的体积是20立方分米。
【点睛】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式,解决问题。
21.(1)96千克;
(2)能
【分析】(1)方钢的体积=方钢的横截面积×方钢的长,方钢的重量=方钢的体积×每立方厘米方钢的重量;
(2)用乘法计算出50根方钢的重量,最后和货车载重量比较大小;据此解答。
【详解】(1)6米=600厘米
4×4×600×0.01
=16×600×0.01
=9600×0.01
=96(千克)
答:这根方钢重96千克
(2)96×50=4800(千克)
因为5000千克>4800千克,所以一辆载重5000千克的货车能一次运载50根这样的方钢。
答:一辆载重5000千克的货车能一次运载50根这样的方钢。
【点睛】根据长方体体积的计算方法求出每根方钢的体积是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
