北师大版八年级下册6.2 平行四边形的判定 课件(共14张PPT)
文档属性
| 名称 | 北师大版八年级下册6.2 平行四边形的判定 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
平行四边形的判定
单击此处添加副标题
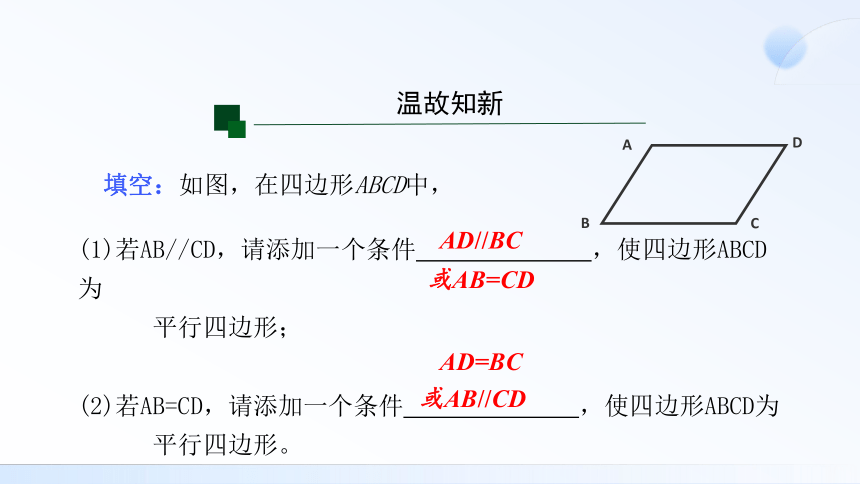
填空:如图,在四边形ABCD中,
(1)若AB//CD,请添加一个条件 ,使四边形ABCD为
平行四边形;
(2)若AB=CD,请添加一个条件 ,使四边形ABCD为
平行四边形。
或AB//CD
AD=BC
或AB=CD
AD//BC
A
B
C
D
温故知新
A
B
C
D
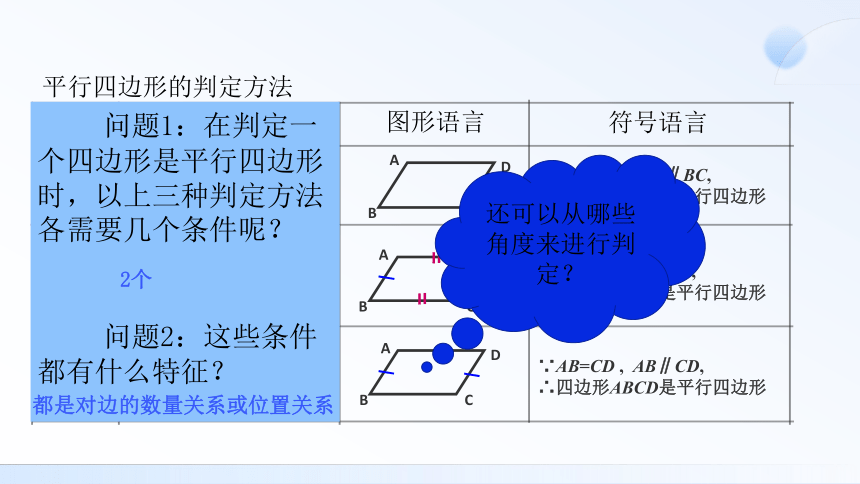
判定
定理1
定理2
定义
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四
边形是平行四边形
两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
∵AB=CD , AD=BC,
∴四边形ABCD是平行四边形
∵AB=CD , AB∥CD,
∴四边形ABCD是平行四边形
A
B
C
D
∵AB∥CD , AD∥BC,
∴四边形ABCD是平行四边形
问题1:在判定一个四边形是平行四边形时,以上三种判定方法各需要几个条件呢?
问题2:这些条件都有什么特征?
2个
都是对边的数量关系或位置关系
A
B
C
D
还可以从哪些角度来进行判定?
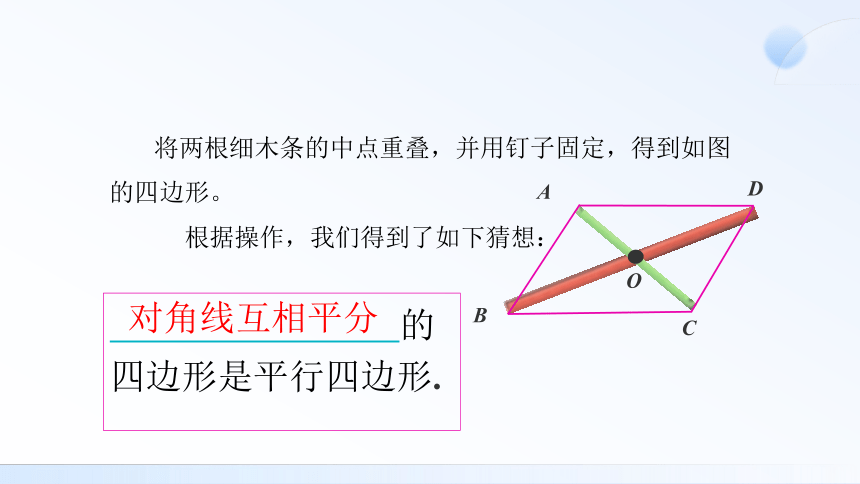
工具:两根不同长度的细木条.
操作:能否合理摆放这两根细木条,使得这两根细木条的
四个端点恰好是一个平行四边形的四个顶点呢?
活动探究
将两根细木条的中点重叠,并用钉子固定,得到如图的四边形。
根据操作,我们得到了如下猜想:
A
B
C
D
O
的 四边形是平行四边形.
对角线互相平分
已知:如图,四边形ABCD的两条对角线AC与BD相交于点O,
并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴ ∠BAO=∠DCO , AB=CD
OA=OC (已知)
OB=OD (已知)
∴△AOB≌△COD(SAS)
∴AB∥ CD , AB= CD.
∴四边形ABCD是平行四边形.
D
B
A
O
C
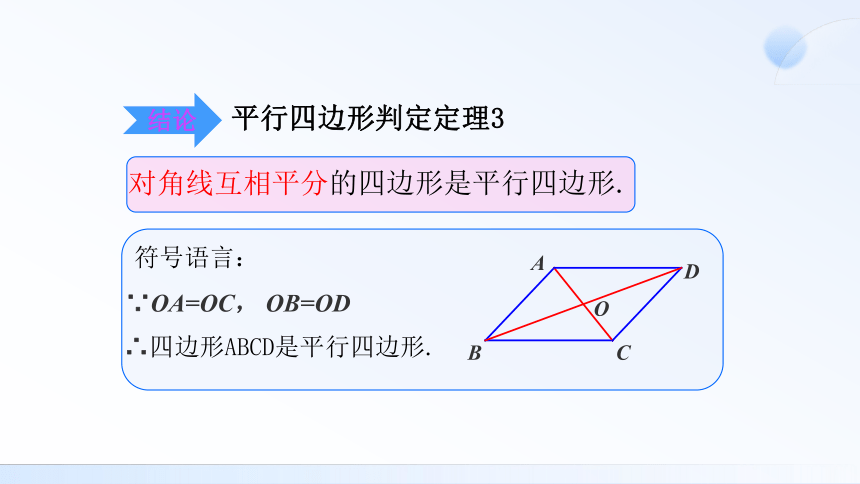
对角线互相平分的四边形是平行四边形.
∵OA=OC,
OB=OD
∴四边形ABCD是平行四边形.
符号语言:
平行四边形判定定理3
结论
D
B
A
O
C
已知:如图,E,F是 ABCD对角线AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:
∴ ∠DAE=∠BCF
∵AE=CF
∴△ADE≌△CBF(SAS)
∴ DE=BF
B
A
C
E
F
D
∵四边形ABCD是平行四边形
∴ AD=CB,AD//CB
同理可得,BE=CF
∴ 四边形BFDE是平行四边形.
学以致用
已知:如图,E,F是 ABCD对角线AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵AE=CF
∴OA-AE=OC-CF
即OE=OF
又 ∵OB=OD,
∴ 四边形BFDE是平行四边形.
B
A
C
E
F
D
O
∵四边形ABCD是平行四边形
∴ OA=OC,OB=OD
变式:若点E,F是直线AC上的两点(如图所示),其他条件不变,
上述结论还成立吗?若成立,请证明;若不成立,请说明理由。
解:上述结论仍成立,理由如下:
连接BD,交AC于点O.
∵AE=CF
∴OA+AE=OC+CF
即OE=OF
又 ∵OB=OD
∴ 四边形BFDE是平行四边形.
C
B
A
E
F
D
∵四边形ABCD是平行四边形
∴ OA=OC,OB=OD
O
2.两组对边分别相等的四边形是平行四边形
从边来判定
1.两组对边分别平行的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
课堂小结
研究路径:
定义
性质
判定
应用
研究内容:
平行四边形的基本元素、相关元素
之间的数量关系与位置关系
研究方法:
合情推理,演绎推理
数学思想:
类比、归纳、转化
互为逆定理
如图,在△ABC中, 点D是AB边上任意一点 , 点E
是BC边的中点 , CF∥AB , 交DE的延长线于点F , 连
接BF,CD.
你能从中得到哪些结论呢?
并尝试证明。
自我评价
如图,在△ABC中, 点D是AB边上任意一点 , 点E是BC边的中点 , CF∥AB , 交DE的延长线于点F , 连接BF,CD.
∵CF∥AB ∴∠ECF=∠EBD
∵E是BC的中点 ∴CE=BE
∵∠CEF=∠BED ∴△CEF≌△BED(ASA),
∴EF=ED ∴四边形CDBF是平行四边形.
解:我的结论是:四边形CDBF是平行四边形
理由如下:
平行四边形的判定
单击此处添加副标题
填空:如图,在四边形ABCD中,
(1)若AB//CD,请添加一个条件 ,使四边形ABCD为
平行四边形;
(2)若AB=CD,请添加一个条件 ,使四边形ABCD为
平行四边形。
或AB//CD
AD=BC
或AB=CD
AD//BC
A
B
C
D
温故知新
A
B
C
D
判定
定理1
定理2
定义
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四
边形是平行四边形
两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
∵AB=CD , AD=BC,
∴四边形ABCD是平行四边形
∵AB=CD , AB∥CD,
∴四边形ABCD是平行四边形
A
B
C
D
∵AB∥CD , AD∥BC,
∴四边形ABCD是平行四边形
问题1:在判定一个四边形是平行四边形时,以上三种判定方法各需要几个条件呢?
问题2:这些条件都有什么特征?
2个
都是对边的数量关系或位置关系
A
B
C
D
还可以从哪些角度来进行判定?
工具:两根不同长度的细木条.
操作:能否合理摆放这两根细木条,使得这两根细木条的
四个端点恰好是一个平行四边形的四个顶点呢?
活动探究
将两根细木条的中点重叠,并用钉子固定,得到如图的四边形。
根据操作,我们得到了如下猜想:
A
B
C
D
O
的 四边形是平行四边形.
对角线互相平分
已知:如图,四边形ABCD的两条对角线AC与BD相交于点O,
并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
∠AOB=∠COD (对顶角相等)
∴ ∠BAO=∠DCO , AB=CD
OA=OC (已知)
OB=OD (已知)
∴△AOB≌△COD(SAS)
∴AB∥ CD , AB= CD.
∴四边形ABCD是平行四边形.
D
B
A
O
C
对角线互相平分的四边形是平行四边形.
∵OA=OC,
OB=OD
∴四边形ABCD是平行四边形.
符号语言:
平行四边形判定定理3
结论
D
B
A
O
C
已知:如图,E,F是 ABCD对角线AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:
∴ ∠DAE=∠BCF
∵AE=CF
∴△ADE≌△CBF(SAS)
∴ DE=BF
B
A
C
E
F
D
∵四边形ABCD是平行四边形
∴ AD=CB,AD//CB
同理可得,BE=CF
∴ 四边形BFDE是平行四边形.
学以致用
已知:如图,E,F是 ABCD对角线AC上的两点,
并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵AE=CF
∴OA-AE=OC-CF
即OE=OF
又 ∵OB=OD,
∴ 四边形BFDE是平行四边形.
B
A
C
E
F
D
O
∵四边形ABCD是平行四边形
∴ OA=OC,OB=OD
变式:若点E,F是直线AC上的两点(如图所示),其他条件不变,
上述结论还成立吗?若成立,请证明;若不成立,请说明理由。
解:上述结论仍成立,理由如下:
连接BD,交AC于点O.
∵AE=CF
∴OA+AE=OC+CF
即OE=OF
又 ∵OB=OD
∴ 四边形BFDE是平行四边形.
C
B
A
E
F
D
∵四边形ABCD是平行四边形
∴ OA=OC,OB=OD
O
2.两组对边分别相等的四边形是平行四边形
从边来判定
1.两组对边分别平行的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
课堂小结
研究路径:
定义
性质
判定
应用
研究内容:
平行四边形的基本元素、相关元素
之间的数量关系与位置关系
研究方法:
合情推理,演绎推理
数学思想:
类比、归纳、转化
互为逆定理
如图,在△ABC中, 点D是AB边上任意一点 , 点E
是BC边的中点 , CF∥AB , 交DE的延长线于点F , 连
接BF,CD.
你能从中得到哪些结论呢?
并尝试证明。
自我评价
如图,在△ABC中, 点D是AB边上任意一点 , 点E是BC边的中点 , CF∥AB , 交DE的延长线于点F , 连接BF,CD.
∵CF∥AB ∴∠ECF=∠EBD
∵E是BC的中点 ∴CE=BE
∵∠CEF=∠BED ∴△CEF≌△BED(ASA),
∴EF=ED ∴四边形CDBF是平行四边形.
解:我的结论是:四边形CDBF是平行四边形
理由如下:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
