北师大版八年级下册6.2 平行四边形的判定 课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级下册6.2 平行四边形的判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 514.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 16:49:10 | ||
图片预览





文档简介
(共19张PPT)
平行四边形的判定(一)
1.平行四边形的定义是什么?
2.平行四边形的性质有哪些?
两组对边分别平行的四边形是平行四边形
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对称性
平行四边形是中心对称图形
对角线
复习回顾
A
B
C
D
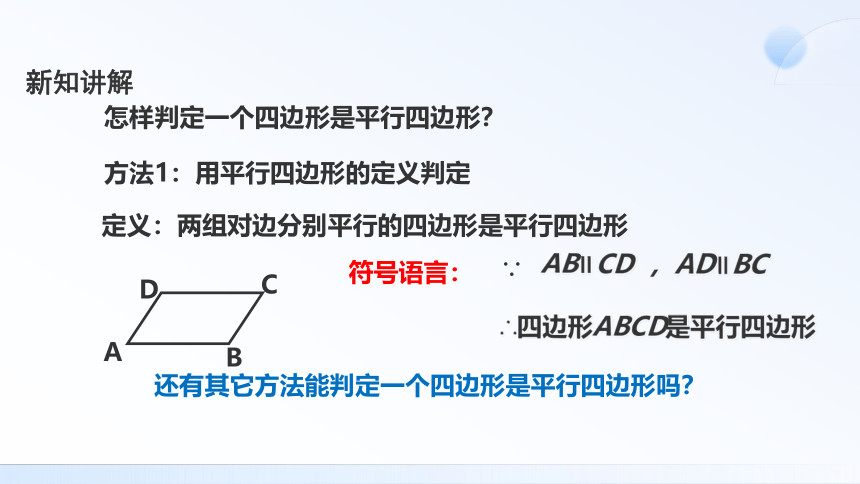
怎样判定一个四边形是平行四边形?
方法1:用平行四边形的定义判定
定义:两组对边分别平行的四边形是平行四边形
还有其它方法能判定一个四边形是平行四边形吗?
A
B
C
D
新知讲解
∴四边形ABCD是平行四边形
,AD∥BC
AB∥CD
∵
符号语言:
活动探究一:做一做 :小组活动,回答下列问题
活动:
工具: 两对长度分别相等的木条;
动手: 能否合理摆放这四根细木条,将其首尾顺次相接搭成一个平行四边形?
思考: 你能说明你得到的四边形是平行四边形吗?
任务一
猜测:两组对边分别相等的四边形是平行四边形
已知:如图,在四边形ABCD中,AB=CD,BC=AD.
∴ 四边形ABCD是平行四边形
证明: 连接BD
在△ABD 和△CDB 中
∴ △ABD ≌△CDB
∴ AB∥CD AD∥CB
求证:四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
∴ ∠ABD=∠CDB ∠ADB=∠CBD
∵ AB=CD AD=CB BD=DB
平行四边形判定定理1:
两组对边分别相等的四边形是平行四边形.
符号语言:
∵ AB=CD,AD=BC
∴ 四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
AB∥CD AD∥BC
AB = CD AD = BC
位置关系
判定定理1 的条件:
我们还有别的研究方向吗?
定义的条件:
数量关系
工具: 两根长度相等的木棒,一组平行线.
动手: 利用给出的工具,能画出一个平行四边形吗?
思考:你如何说明你所画出的四边形是平行四边形吗?
活动探究二:做一做 :小组活动,回答下列问题。
任务二
图形展示:木棒:AD=BC,平行线:EF∥GH
A
B
D
C
等腰梯形
A
D
C
B
平行四边形
E
G
F
H
猜测:一组对边平行且相等的四边形是平行四边形
A
B
D
C
平行四边形
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
∵AD=BC,∠DAC=∠ACB,AC=CA
∴ΔABC ≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴ 四边形ABCD是平行四边形( 平行四边形的定义)
已知:在四边形ABCD中, AD B BC 。
B
D
C
A
在△ABC和△CDA 中
又∵AD∥BC
∵ AD=BC,AD∥BC
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形
符号语言为:
平行四边形的判定定理2:
A
B
C
D
A
B
C
D
对边的位置关系和数量关系结合,来研究平行四边形的判定
AB = CD ①
AD = BC ②
数量关系:
AB∥CD
位置关系:
AD∥BC
AB = CD ③
AD = BC ④
√
√
在下列条件中,不能判定四边形ABCD是平行四边形的是( )
AB=CD,AD∥BC
AB=CD,AB ∥CD
(C)AB∥CD, AD∥BC
(D) AB=CD,AD=BC
A
课堂检测
一组对边平行,另一组对边相等
一组对边平行且相等
两组对边分别平行
两组对边分别相等
A
B
D
C
A
B
C
D
已知:在四边形ABCD中,AB∥CD,要使四边形ABCD为
平行四边形,需添加一个条件是什么?
A
B
C
D
解:AD∥BC
或 AB=CD
已知:如图,在平行四边形ABCD中,E、F 分别是AD
和BC 的中点.
求证:四边形BFDE是平行四边形.
∴ 四边形BFDE 是平行四边形
证明:∵ 四边形ABCD是平行四边形
∴ AD=CB AD∥BC
又∵E、F 分别是AD和BC的 中点
∴ DE=BF
又∵ED∥BF
∴ ED= AD , BF= BC
( 一组对边平行且相等的四边形是平行四边形)
从边来判定
1.两组对边分别平行的四边形是平行四边形
(定义)
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
平行四边形的判定方法
课堂小结
谢 谢 !
thank you
平行四边形的判定(一)
1.平行四边形的定义是什么?
2.平行四边形的性质有哪些?
两组对边分别平行的四边形是平行四边形
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对称性
平行四边形是中心对称图形
对角线
复习回顾
A
B
C
D
怎样判定一个四边形是平行四边形?
方法1:用平行四边形的定义判定
定义:两组对边分别平行的四边形是平行四边形
还有其它方法能判定一个四边形是平行四边形吗?
A
B
C
D
新知讲解
∴四边形ABCD是平行四边形
,AD∥BC
AB∥CD
∵
符号语言:
活动探究一:做一做 :小组活动,回答下列问题
活动:
工具: 两对长度分别相等的木条;
动手: 能否合理摆放这四根细木条,将其首尾顺次相接搭成一个平行四边形?
思考: 你能说明你得到的四边形是平行四边形吗?
任务一
猜测:两组对边分别相等的四边形是平行四边形
已知:如图,在四边形ABCD中,AB=CD,BC=AD.
∴ 四边形ABCD是平行四边形
证明: 连接BD
在△ABD 和△CDB 中
∴ △ABD ≌△CDB
∴ AB∥CD AD∥CB
求证:四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形)
∴ ∠ABD=∠CDB ∠ADB=∠CBD
∵ AB=CD AD=CB BD=DB
平行四边形判定定理1:
两组对边分别相等的四边形是平行四边形.
符号语言:
∵ AB=CD,AD=BC
∴ 四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
AB∥CD AD∥BC
AB = CD AD = BC
位置关系
判定定理1 的条件:
我们还有别的研究方向吗?
定义的条件:
数量关系
工具: 两根长度相等的木棒,一组平行线.
动手: 利用给出的工具,能画出一个平行四边形吗?
思考:你如何说明你所画出的四边形是平行四边形吗?
活动探究二:做一做 :小组活动,回答下列问题。
任务二
图形展示:木棒:AD=BC,平行线:EF∥GH
A
B
D
C
等腰梯形
A
D
C
B
平行四边形
E
G
F
H
猜测:一组对边平行且相等的四边形是平行四边形
A
B
D
C
平行四边形
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
∵AD=BC,∠DAC=∠ACB,AC=CA
∴ΔABC ≌ΔCDA
∴∠BAC=∠ACD
∴AB∥CD
∴ 四边形ABCD是平行四边形( 平行四边形的定义)
已知:在四边形ABCD中, AD B BC 。
B
D
C
A
在△ABC和△CDA 中
又∵AD∥BC
∵ AD=BC,AD∥BC
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形
符号语言为:
平行四边形的判定定理2:
A
B
C
D
A
B
C
D
对边的位置关系和数量关系结合,来研究平行四边形的判定
AB = CD ①
AD = BC ②
数量关系:
AB∥CD
位置关系:
AD∥BC
AB = CD ③
AD = BC ④
√
√
在下列条件中,不能判定四边形ABCD是平行四边形的是( )
AB=CD,AD∥BC
AB=CD,AB ∥CD
(C)AB∥CD, AD∥BC
(D) AB=CD,AD=BC
A
课堂检测
一组对边平行,另一组对边相等
一组对边平行且相等
两组对边分别平行
两组对边分别相等
A
B
D
C
A
B
C
D
已知:在四边形ABCD中,AB∥CD,要使四边形ABCD为
平行四边形,需添加一个条件是什么?
A
B
C
D
解:AD∥BC
或 AB=CD
已知:如图,在平行四边形ABCD中,E、F 分别是AD
和BC 的中点.
求证:四边形BFDE是平行四边形.
∴ 四边形BFDE 是平行四边形
证明:∵ 四边形ABCD是平行四边形
∴ AD=CB AD∥BC
又∵E、F 分别是AD和BC的 中点
∴ DE=BF
又∵ED∥BF
∴ ED= AD , BF= BC
( 一组对边平行且相等的四边形是平行四边形)
从边来判定
1.两组对边分别平行的四边形是平行四边形
(定义)
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
平行四边形的判定方法
课堂小结
谢 谢 !
thank you
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
