北师大版数学七年级下册 1.4.3 多项式乘多项式 教案(表格式)
文档属性
| 名称 | 北师大版数学七年级下册 1.4.3 多项式乘多项式 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 236.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 数学(北师大版) 年级 七年级 学期 春季
课题 多项式乘多项式
教学目标
通过现实情境导入课题,借助数变化的图形,经历观察、类比、分析、归纳、总结,自主建构多项式乘多项式的运算法则; (2)能借助图形解释整式乘法的法则,发展几何直观; (3)掌握多项式乘多项式的运算法则并能够进行化简运算.
教学内容
教学重点: 1. 多项式乘多项式的运算法则的理解及运用; 教学难点: 1. 多项式乘多项式的运算法则的运用及符号的处理。
教学过程
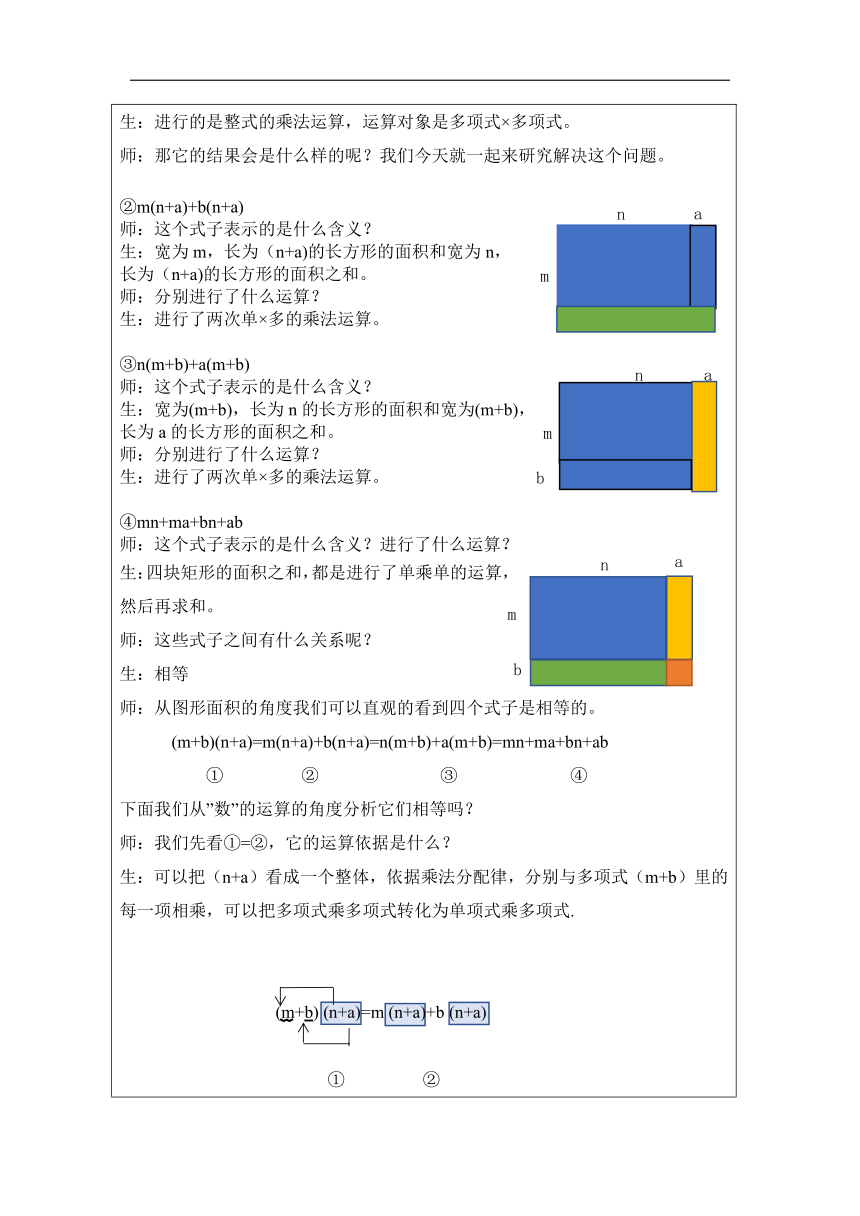
设置情境,复习旧知,引入新课 由于我校被评为足球特色学校,为了大力发展体育运动,学校决定增加学校足球场的面积。 情境一、学校操场为宽m米,长n米的长方形球场,则原足球场的面积为 mn平方米. 师:在算面积的时候,我们进行了什么运算?运算对象是?所得的结果是? 生:进行了整式的乘法运算,运算对象是单项式×单项式,运算所得的结果仍然是单项式。 单×单 m · n=mn 整式的乘法 单×多 …… 情境二、一期工程,在操场东侧(右侧)拓宽a米,则经过施 工改造后的操场面积为 m(n+a)或(mn+ma) 平方米 . 师:你是怎么得到的? 生1:把操场看成一个整体,是一个宽为m米,长为(n+a)的大矩形,因此面积为m(n+a); 生2:把操场看成由两个小矩形拼成,分别算面积以后求和,就可以得到mn+ma 师:那它们的含义都是表示? 生:矩形的面积。 师: 从“形”的角度,它们面积是相等的,我们可以得到: m(n+a)=mn+ma, 从“数”的角度,这个式子我们进行了什么运算?运算对象是什么?运算结果是? 生:进行了单项式 多项式的运算,运算结果是一个多项式. 师:那结果多项式的项数有几项?这个项数由谁决定? 生:单乘多的运算结果是二项式,结果的项数与乘数里多项式的项数一致。 师:单项式 多项式的法则是? 生:单项式与多项式相乘就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。 师:其实我们在进行单项式 多项式的运算时,就是利用乘法分配律,把单项式乘多项式转化为了单项式乘单项式的运算。 单×单 m · n=mn 整式的乘法 单×多 m (n+a)=mn+ma …… 二、探索思考,获得新知 情境三、为了让学生活动更加丰富,学校决定二期工程继续拓宽操场,修建一处乒乓球台.此次拓宽向操场南面(下方)拓宽b米,则新操场的面积为 ?你可以怎么表示?(多种表示方法) 生:①(m+b)(n+a) 师:这里我们进行的是什么运算?它的运算对象是? 生:进行的是整式的乘法运算,运算对象是多项式×多项式。 师:那它的结果会是什么样的呢?我们今天就一起来研究解决这个问题。 ②m(n+a)+b(n+a) 师:这个式子表示的是什么含义? 生:宽为m,长为(n+a)的长方形的面积和宽为n,长为(n+a)的长方形的面积之和。 师:分别进行了什么运算? 生:进行了两次单×多的乘法运算。 ③n(m+b)+a(m+b) 师:这个式子表示的是什么含义? 生:宽为(m+b),长为n的长方形的面积和宽为(m+b), 长为a的长方形的面积之和。 师:分别进行了什么运算? 生:进行了两次单×多的乘法运算。 ④mn+ma+bn+ab 师:这个式子表示的是什么含义?进行了什么运算? 生:四块矩形的面积之和,都是进行了单乘单的运算,然后再求和。 师:这些式子之间有什么关系呢? 生:相等 师:从图形面积的角度我们可以直观的看到四个式子是相等的。 (m+b)(n+a)=m(n+a)+b(n+a)=n(m+b)+a(m+b)=mn+ma+bn+ab ① ② ③ ④ 下面我们从”数”的运算的角度分析它们相等吗? 师:我们先看①=②,它的运算依据是什么? 生:可以把(n+a)看成一个整体,依据乘法分配律,分别与多项式(m+b)里的每一项相乘,可以把多项式乘多项式转化为单项式乘多项式. (m+b) (n+a)=m (n+a)+b (n+a) ① ② 师:那么类似地,怎么由①得到③ 呢? 生:把①中的(m+b)看做一个整体,依据乘法分配律,分别与多项式(n+a)里的每一项相乘. (m+b)(n+a)=n (m+b)+a (m+b) ① ③ 师:它们看作单乘多后的结果也是多项式,项数可以看成是有两项,和乘数里的多项式项数相同。 师:我们继续分析②=④,它的运算依据是什么? 生:这一步利用乘法分配律,把单项式乘多项式转化为单项式乘单项式. m(n+a)+b(n+a)=mn+ma+bn+ab 师:请大家思考,我们能直接由①得到④吗? (m + b)(n + a)=m(n + a)+b(n + a)=mn + ma + bn + ab ① ②/③ ④ 多×多 单×多 单×单 师追问:如果,直接得到(m+b)(n+a)=mn+ma+bn+ab,你能用文字归纳如何进行多项式与多项式的相乘吗? 生:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加. 师:运算的对象是?运算的结果是?运算结果的项数是?由谁决定? 生:进行的是多乘多的运算,得到的是多项式,结果的项数是由两个多项式的项数相乘得到的。 师:因此多项式乘多项式运算,可以看成经过两次转化思想之后,变成单项式乘单项式的运算。 单×单 m · n=mn 整式的乘法 单×多 m (n+a)=mn+ma 多×多 (m+b) (n+a)=mn+ma+bn+ab 三、夯实基础,巩固新知 例1:计算 (1); (2); (3); (4). 【练一练】 (1); (2); ; (4). (学生先做后上黑板,让其他学生上去纠错) 【想一想】 在计算多项式与多项式的乘法时要注意那些问题?你有什么防止错误的好办法吗?谈谈你的想法。 生:1.要防止两个多项式相乘,直接写出结果时“漏项”。 检查办法是: 两个多项式相乘,在没有合并同类项之前,积的项数应该是这两个多项式项数的积。 2.如果有同类项,则应该合并同类项,得出最简结果。 3.要注意符号。防止错误的办法:可以把运算符号当成性质符号来处理,变减法为加法,防止符号错误. 通过刚才的计算练习,老师发现大家对多乘多的计算已经开始熟悉起来了,那下面,我们来运用我们所学的知识,来解决一下实际问题。 例2:如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长为(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化. (1)用含a,b的代数式表示需要硬化的面积并化简 ; (2)当a=5,b=2时,求需要硬化的面积. 第一问(1)有了刚才数形结合的经验(点),(点)我们可以很快表示出来S阴=S大-S小,第二问注意要把带入的过程体现出来。答案大家参考一下。 四、活动探索,能力升华 1.观察例1的计算结果,为什么多乘多得到的结果分别为四项式、三项式、二项式? 多乘多的结果仍为多项式,项数由所乘多项式的项数决定,结果是四项,但是有时通过合并同类项把一些项消去或者合并了。那什么时候能消去?什么时候会合并,我们下节课继续来探索。 五、课堂小结: (1) 本节课你学到了什么?
(2) 你用到了什么样的数学思想和方法?我们是如何对多项式乘多项式展开研究的? (3) 你还有哪些困惑?请与同学们交流. 这几节课,我们类比数的运算研究了整式的加减乘运算,他们有相同的运算法则和运算律,今天我们学习的多乘多可以经过两次转化成为单乘单的运算,类比我们数与数的运算就不再复杂了。以后我们还会类比对数的学习,研究更多式的内容。
课程基本信息
学科 数学(北师大版) 年级 七年级 学期 春季
课题 多项式乘多项式
教学目标
通过现实情境导入课题,借助数变化的图形,经历观察、类比、分析、归纳、总结,自主建构多项式乘多项式的运算法则; (2)能借助图形解释整式乘法的法则,发展几何直观; (3)掌握多项式乘多项式的运算法则并能够进行化简运算.
教学内容
教学重点: 1. 多项式乘多项式的运算法则的理解及运用; 教学难点: 1. 多项式乘多项式的运算法则的运用及符号的处理。
教学过程
设置情境,复习旧知,引入新课 由于我校被评为足球特色学校,为了大力发展体育运动,学校决定增加学校足球场的面积。 情境一、学校操场为宽m米,长n米的长方形球场,则原足球场的面积为 mn平方米. 师:在算面积的时候,我们进行了什么运算?运算对象是?所得的结果是? 生:进行了整式的乘法运算,运算对象是单项式×单项式,运算所得的结果仍然是单项式。 单×单 m · n=mn 整式的乘法 单×多 …… 情境二、一期工程,在操场东侧(右侧)拓宽a米,则经过施 工改造后的操场面积为 m(n+a)或(mn+ma) 平方米 . 师:你是怎么得到的? 生1:把操场看成一个整体,是一个宽为m米,长为(n+a)的大矩形,因此面积为m(n+a); 生2:把操场看成由两个小矩形拼成,分别算面积以后求和,就可以得到mn+ma 师:那它们的含义都是表示? 生:矩形的面积。 师: 从“形”的角度,它们面积是相等的,我们可以得到: m(n+a)=mn+ma, 从“数”的角度,这个式子我们进行了什么运算?运算对象是什么?运算结果是? 生:进行了单项式 多项式的运算,运算结果是一个多项式. 师:那结果多项式的项数有几项?这个项数由谁决定? 生:单乘多的运算结果是二项式,结果的项数与乘数里多项式的项数一致。 师:单项式 多项式的法则是? 生:单项式与多项式相乘就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。 师:其实我们在进行单项式 多项式的运算时,就是利用乘法分配律,把单项式乘多项式转化为了单项式乘单项式的运算。 单×单 m · n=mn 整式的乘法 单×多 m (n+a)=mn+ma …… 二、探索思考,获得新知 情境三、为了让学生活动更加丰富,学校决定二期工程继续拓宽操场,修建一处乒乓球台.此次拓宽向操场南面(下方)拓宽b米,则新操场的面积为 ?你可以怎么表示?(多种表示方法) 生:①(m+b)(n+a) 师:这里我们进行的是什么运算?它的运算对象是? 生:进行的是整式的乘法运算,运算对象是多项式×多项式。 师:那它的结果会是什么样的呢?我们今天就一起来研究解决这个问题。 ②m(n+a)+b(n+a) 师:这个式子表示的是什么含义? 生:宽为m,长为(n+a)的长方形的面积和宽为n,长为(n+a)的长方形的面积之和。 师:分别进行了什么运算? 生:进行了两次单×多的乘法运算。 ③n(m+b)+a(m+b) 师:这个式子表示的是什么含义? 生:宽为(m+b),长为n的长方形的面积和宽为(m+b), 长为a的长方形的面积之和。 师:分别进行了什么运算? 生:进行了两次单×多的乘法运算。 ④mn+ma+bn+ab 师:这个式子表示的是什么含义?进行了什么运算? 生:四块矩形的面积之和,都是进行了单乘单的运算,然后再求和。 师:这些式子之间有什么关系呢? 生:相等 师:从图形面积的角度我们可以直观的看到四个式子是相等的。 (m+b)(n+a)=m(n+a)+b(n+a)=n(m+b)+a(m+b)=mn+ma+bn+ab ① ② ③ ④ 下面我们从”数”的运算的角度分析它们相等吗? 师:我们先看①=②,它的运算依据是什么? 生:可以把(n+a)看成一个整体,依据乘法分配律,分别与多项式(m+b)里的每一项相乘,可以把多项式乘多项式转化为单项式乘多项式. (m+b) (n+a)=m (n+a)+b (n+a) ① ② 师:那么类似地,怎么由①得到③ 呢? 生:把①中的(m+b)看做一个整体,依据乘法分配律,分别与多项式(n+a)里的每一项相乘. (m+b)(n+a)=n (m+b)+a (m+b) ① ③ 师:它们看作单乘多后的结果也是多项式,项数可以看成是有两项,和乘数里的多项式项数相同。 师:我们继续分析②=④,它的运算依据是什么? 生:这一步利用乘法分配律,把单项式乘多项式转化为单项式乘单项式. m(n+a)+b(n+a)=mn+ma+bn+ab 师:请大家思考,我们能直接由①得到④吗? (m + b)(n + a)=m(n + a)+b(n + a)=mn + ma + bn + ab ① ②/③ ④ 多×多 单×多 单×单 师追问:如果,直接得到(m+b)(n+a)=mn+ma+bn+ab,你能用文字归纳如何进行多项式与多项式的相乘吗? 生:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加. 师:运算的对象是?运算的结果是?运算结果的项数是?由谁决定? 生:进行的是多乘多的运算,得到的是多项式,结果的项数是由两个多项式的项数相乘得到的。 师:因此多项式乘多项式运算,可以看成经过两次转化思想之后,变成单项式乘单项式的运算。 单×单 m · n=mn 整式的乘法 单×多 m (n+a)=mn+ma 多×多 (m+b) (n+a)=mn+ma+bn+ab 三、夯实基础,巩固新知 例1:计算 (1); (2); (3); (4). 【练一练】 (1); (2); ; (4). (学生先做后上黑板,让其他学生上去纠错) 【想一想】 在计算多项式与多项式的乘法时要注意那些问题?你有什么防止错误的好办法吗?谈谈你的想法。 生:1.要防止两个多项式相乘,直接写出结果时“漏项”。 检查办法是: 两个多项式相乘,在没有合并同类项之前,积的项数应该是这两个多项式项数的积。 2.如果有同类项,则应该合并同类项,得出最简结果。 3.要注意符号。防止错误的办法:可以把运算符号当成性质符号来处理,变减法为加法,防止符号错误. 通过刚才的计算练习,老师发现大家对多乘多的计算已经开始熟悉起来了,那下面,我们来运用我们所学的知识,来解决一下实际问题。 例2:如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长为(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化. (1)用含a,b的代数式表示需要硬化的面积并化简 ; (2)当a=5,b=2时,求需要硬化的面积. 第一问(1)有了刚才数形结合的经验(点),(点)我们可以很快表示出来S阴=S大-S小,第二问注意要把带入的过程体现出来。答案大家参考一下。 四、活动探索,能力升华 1.观察例1的计算结果,为什么多乘多得到的结果分别为四项式、三项式、二项式? 多乘多的结果仍为多项式,项数由所乘多项式的项数决定,结果是四项,但是有时通过合并同类项把一些项消去或者合并了。那什么时候能消去?什么时候会合并,我们下节课继续来探索。 五、课堂小结: (1) 本节课你学到了什么?
(2) 你用到了什么样的数学思想和方法?我们是如何对多项式乘多项式展开研究的? (3) 你还有哪些困惑?请与同学们交流. 这几节课,我们类比数的运算研究了整式的加减乘运算,他们有相同的运算法则和运算律,今天我们学习的多乘多可以经过两次转化成为单乘单的运算,类比我们数与数的运算就不再复杂了。以后我们还会类比对数的学习,研究更多式的内容。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
