3.1 图形的平移以及平移的性质 教案(无答案)
文档属性
| 名称 | 3.1 图形的平移以及平移的性质 教案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 678.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览


文档简介
教学设计
课题 图形的平移以及平移的性质 授课人
教 学 目 标 知识技能 1.认识平移,说出平移的定义,理解平移的基本内涵; 2.理解并能掌握平移的基本性质.
过程方法 经历有关平移的观察、操作、分析及抽象、概括等过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念,会画简单的平移图形.
情感态度与价值观 通过收集自己身边“平移”的实例,感受“生活处处有数学”,激发学生学习数学的兴趣;通过欣赏生活中的平移图形与学生自己设计平移图案,使学生感受数学美.
教学 重点 探索图形平移的主要特征和基本性质,会画简单图形的平移图.
教学 难点 探索和理解平移的基本性质.
授课 类型 新授课 课时 1
教具 多媒体课件
教学活动
教学 步骤 师生活动 设计意图
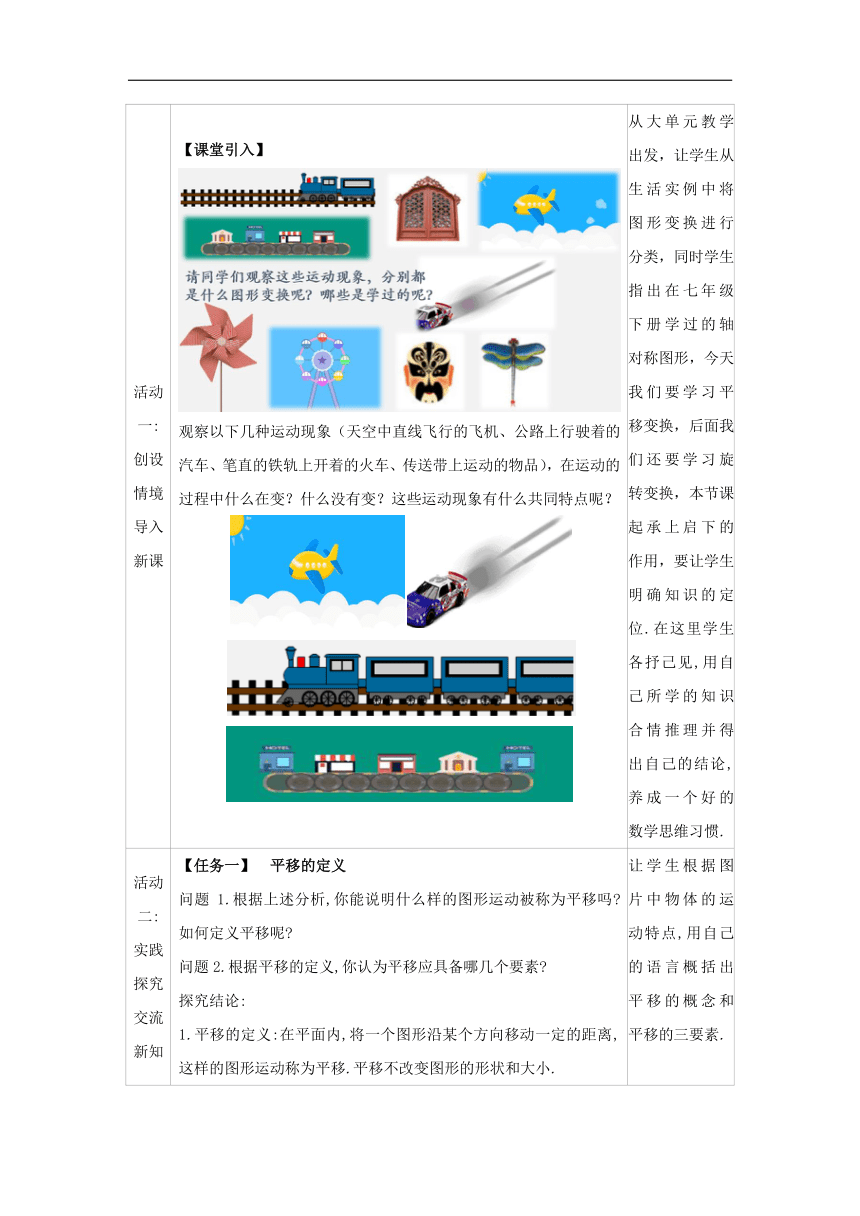
活动 一: 创设 情境 导入 新课 【课堂引入】 观察以下几种运动现象(天空中直线飞行的飞机、公路上行驶着的汽车、笔直的铁轨上开着的火车、传送带上运动的物品),在运动的过程中什么在变?什么没有变?这些运动现象有什么共同特点呢? 从大单元教学出发,让学生从生活实例中将图形变换进行分类,同时学生指出在七年级下册学过的轴对称图形,今天我们要学习平移变换,后面我们还要学习旋转变换,本节课起承上启下的作用,要让学生明确知识的定位.在这里学生各抒己见,用自己所学的知识合情推理并得出自己的结论,养成一个好的数学思维习惯.
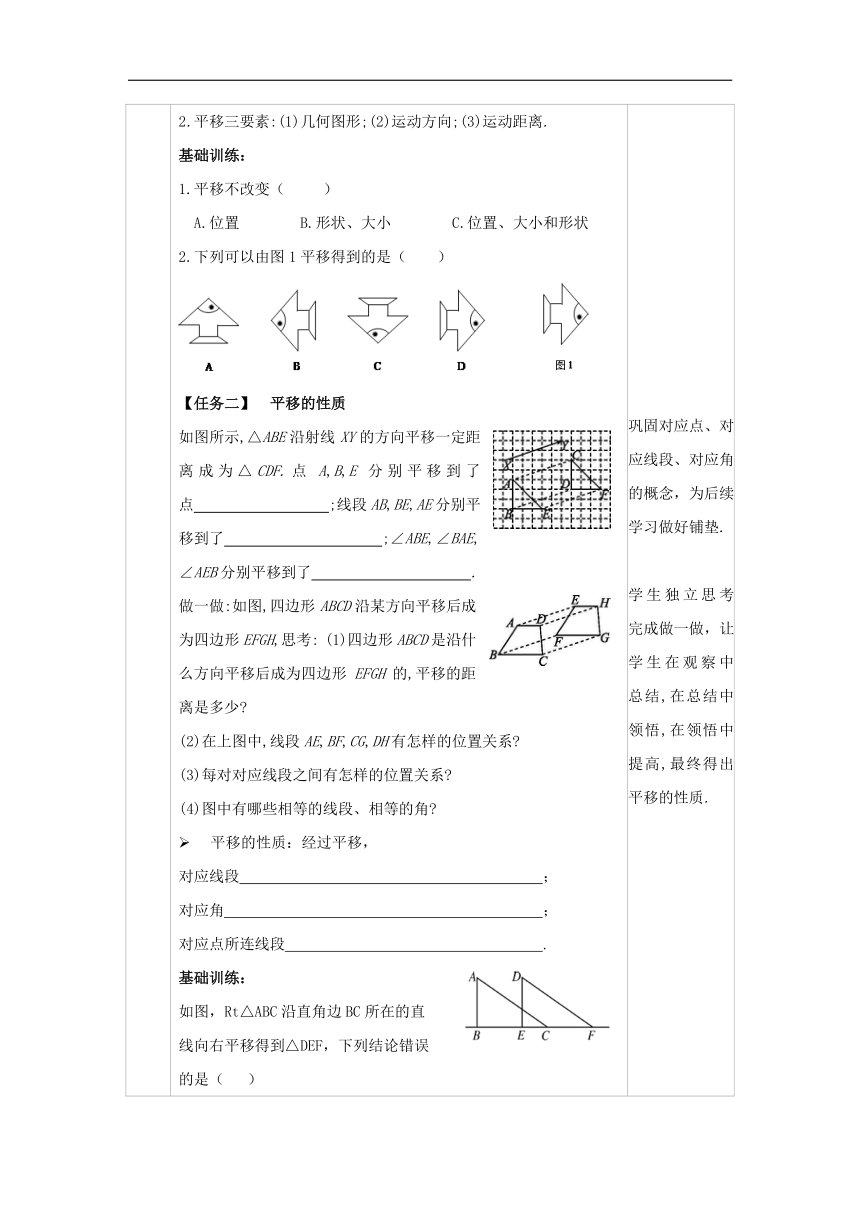
活动 二: 实践 探究 交流 新知 【任务一】 平移的定义 问题1.根据上述分析,你能说明什么样的图形运动被称为平移吗 如何定义平移呢 问题2.根据平移的定义,你认为平移应具备哪几个要素 探究结论: 1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移不改变图形的形状和大小. 2.平移三要素:(1)几何图形;(2)运动方向;(3)运动距离. 基础训练: 1.平移不改变( ) A.位置 B.形状、大小 C.位置、大小和形状 2.下列可以由图1平移得到的是( ) 【任务二】 平移的性质 如图所示,△ABE沿射线XY的方向平移一定距离成为△CDF.点A,B,E分别平移到了点 ;线段AB,BE,AE分别平移到了 ;∠ABE,∠BAE,∠AEB分别平移到了 . 做一做:如图,四边形ABCD沿某方向平移后成为四边形EFGH,思考: (1)四边形ABCD是沿什么方向平移后成为四边形EFGH的,平移的距离是多少 (2)在上图中,线段AE,BF,CG,DH有怎样的位置关系 (3)每对对应线段之间有怎样的位置关系 (4)图中有哪些相等的线段、相等的角 平移的性质:经过平移, 对应线段 ; 对应角 ; 对应点所连线段 . 基础训练: 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论错误的是( ) A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF 【任务三】 平移作图 1.如图,经过平移,△ABC的顶点A移到了点D. (1)指出平移的方向和平移的距离; (2)画出平移后的三角形. 2.你还有其他的画法吗 与同伴交流. 3.确定一个图形平移后的位置,需要知道哪些条件 画法一:过点D分别作出与AB,AC平行且相等的线段DE,DF,连接EF,△DEF就是△ABC平移后的图形. 画法二:因为平移后的图形与原图形全等,所以过点B作线段BE,使它与线段AD平行且相等,得到另一个对应点E,用同样的方法得到点C的对应点F,连接DE,EF,FD.△DEF就是△ABC平移后的图形. 确定一个图形平移后的位置,需要以下条件: (1)图形原来的位置.(2)平移的方向.(3)平移的距离. 拓展讲解: 1.平移作图的关键是掌握平移变换的定义和性质,由此作出各个关键点的对应点,顺次连线. 2.对应点的连线属于辅助线,一般画成虚线;对应线段属于平移前后的两个图形的部分,一般画成实线,二者不能混淆. 3.画平行线可以借助推三角尺的方法. 基础训练: 1.如图,在△ABC中,BC= 3cm.将△ABC沿射线BC向右平移4 cm得到△DEF,则BF的长为( ) A.4 cm B.7 cm C.8 cm D.10 cm 2.如图,将周长为8的△ABC沿BC边向右平移2个单位长度得到△DEF,则四边形ABFD的周长为 . 3.如图,在由边长均为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点C移到了点C'的位置. (1)画出平移后的△A'B'C'(点A'与点A对应,点B'与点B对应); (2)指出平移的方向和平移的距离. 让学生根据图片中物体的运动特点,用自己的语言概括出平移的概念和平移的三要素. 巩固对应点、对应线段、对应角的概念,为后续学习做好铺垫. 学生独立思考完成做一做,让学生在观察中总结,在总结中领悟,在领悟中提高,最终得出平移的性质. 学生自己动手画图,按照自己的方法画出平移后的三角形.给学生留出足够的时间来思考,让学生充分交流后总结画图方法以及确定平移后的图形的条件.
活动 三: 开放 训练 体现 应用 【期中、期末链接】 基础训练: 1.(2015-2016)如图,将三角尺ABC的一边AC沿位置固定的直尺推移得到△DEF,下列结论不一定正确的是( ) A.DE∥AB B.四边形ABED是平行四边形 C.AD∥BE D.AD=AB 2.(2016-2017)如图,将线段AB沿箭头方向平移2cm得到线段CD,若AB=3cm,则四边形ABDC的周长为( ) A.8cm B.10cm C.12cm D.20cm 3.(2017-2018)如图,在△ABC中,AB=8,BC=12,∠B=60°,将△ABC沿着射线BC的方向平移得到△A’ B’C’,连接A’C,若BB’=4,则△A’B’C的周长为( ) A.20 B.24 C.36 D.16 4.(2019-2020)如图,△ABC沿线段BA方向平移得到△DEF,若AB=6,AE=2.则平移的距离为( ) A.2 B.4 C.6 D.8 5.(2020-2021)如图,△ABC中,AB=BC=8cm,将△ABC沿BC平移3cm得到△DEF,AC与DE相交于点G,则GE的长为 cm. 能力提升: 6.(2021-2022)如图,Rt△ABC中,∠BAC=90°,将△ABC沿BC方向平移得到△DEF,其中A,B,C的对应点分别是点D,E,F,DE与AC交于点G.若点E是BC的中点,则下列结论中不一定正确的是( ) A.AB=DE B. C.AC与DE互相垂直平分 D.∠DAG=∠DEC 【当堂检测】 基础训练: 1.下列说法中正确的是( ) A.一个图形经过平移后,与原图形成轴对称 B.如果两个图形成轴对称,那么一个图形可由另一个图形经过平移变换得到 C.一个图形经过平移后,它的性质都发生了变化 D.图形的平移由平移的方向和距离决定 2.在以下现象中,属于平移的是( ) ①在荡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动. A.①② B.①③ C.②③ D.②④ 3.如图,大长方形的长是10 cm,宽是8 cm,阴影部分的宽均为2 cm,则空白部分的面积是( ) A.36 cm2 B.40 cm2 C.32 cm2 D.48 cm2 4.如果△ABC沿着北偏东30°的方向移动了2 cm,那么△ABC的边AB上的一点P向 移动了 cm. 5.下列说法:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长不变;④△ABC在平移过程中,面积不变.其中正确的有 (填序号). 能力提升: (2021-2022太原期末) 如图,Rt△ABC中,∠BAC=90°,将△ABC沿BC方向平移得到△DEF,其中A,B,C的对应点分别是点D,E,F,DE与AC交于点G.若点E是BC的中点,则下列结论中不一定正确的是( ) A.AB=DE B. C.AC与DE互相垂直平分 D.∠DAG=∠DEC 通过对期中、期末真题的练习,让学生进一步认识平移,理解平移的基本内涵,理解平移前后两个图形对应点连线平行且相等、对应线段和对应角分别相等的性质. 进一步深化学生对平移的特征的理解,提高学生运用平移特征解决实际问题的能力. 学以致用,课上完成当堂检测,及时了解学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高.
活动 四: 课后 反馈查漏补缺 【课后反馈】 基础达标: 1.下列车标,可看作图案的某一部分经过平移所形成的是( ) A. B. C. D. 2.下列几种运动属于平移的有( ) ①水平运输带上的砖的运动;②电脑的风叶的运动;③升降机上下做机械运动;④足球场上足球的运动. A. 一种 B. 两种 C. 三种 D. 四种 3.下列现象属于平移的是( ) ①打气筒活塞的轮复运动;②电梯的上下运动;③钟摆的摆动;④转动的门;⑤汽车在一条笔直的马路上行走. A. ③ B. ②③ C. ①②④ D. ①②⑤ 4.平移前后两个图形是全等图形,对应点连线( ) A. 平行但不相等 B. 不平行也不相等 C. 平行且相等 D. 不相等 5.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( ) A.平行四边形 B.等腰梯形 C.正六边形 D.圆 6.经过平移,△ABC移到△DEF的位置,如图. 下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF. 其中正确的有( ) A. 0个 B. 1个 C. 2个 D. 3个 7.下列平移图错误的是( ) 能力提升: 8.某景点拟在如图所示的长方形荷塘上架设小桥,若荷塘中小桥的总长为50 m,则荷塘周长为_______m. 9.如图,将直径为的半圆水平向左平移,则半圆所扫过的面积(阴影部分)为( ) A. B. C. D. 拓展延伸: 10.如图所示的4×6正方形网格纸中,小正方形的顶点称为格点,如△ABC的三个顶点都在格点上,平移△ABC,使平移后顶点在格点上,且整个△ABC都在网格纸内,则有_______种不同的平移方法(不同移法但移到同一位置的算同一种). 课后完成课后反馈,让学生能够主动认真完成,同时巩固新课,能够从练习中发现自己的问题,继续深入学习,查漏补缺.
活动 五: 课堂 总结 效果反思 【板书设计】 图形的平移简单应用 框架图式总结,更容易形成知识网络.
【教学反思】 ①[授课流程反思] 本节课通过生活实例,让学生去感受平移,理解平移,为归纳平移的定义及其性质打下基础,使学生深刻感受到数学来源于生活.让学生会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言语言表达现实世界. ②[讲授效果反思] 本节课的教学中,通过实例让学生归纳总结平移的定义及平移的性质.通过画图,培养学生的空间几何思维.让学生经历从生活到数学的抽象过程,培养学生的抽象思维能力.通过大量真题,让学生了解本节内容在期中期末的考题,让学生心里有数,最后在通过检测,了解到学生的掌握情况. ③[学生状态反思] 通过学生的练习反馈,了解了大部分学生能够掌握平移,理解平移的基本内涵,同时能够运用平移的性质解题,让学生养成理论联系实际的习惯,发展学生的实践能力. 教学反思,提升自我.
课题 图形的平移以及平移的性质 授课人
教 学 目 标 知识技能 1.认识平移,说出平移的定义,理解平移的基本内涵; 2.理解并能掌握平移的基本性质.
过程方法 经历有关平移的观察、操作、分析及抽象、概括等过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念,会画简单的平移图形.
情感态度与价值观 通过收集自己身边“平移”的实例,感受“生活处处有数学”,激发学生学习数学的兴趣;通过欣赏生活中的平移图形与学生自己设计平移图案,使学生感受数学美.
教学 重点 探索图形平移的主要特征和基本性质,会画简单图形的平移图.
教学 难点 探索和理解平移的基本性质.
授课 类型 新授课 课时 1
教具 多媒体课件
教学活动
教学 步骤 师生活动 设计意图
活动 一: 创设 情境 导入 新课 【课堂引入】 观察以下几种运动现象(天空中直线飞行的飞机、公路上行驶着的汽车、笔直的铁轨上开着的火车、传送带上运动的物品),在运动的过程中什么在变?什么没有变?这些运动现象有什么共同特点呢? 从大单元教学出发,让学生从生活实例中将图形变换进行分类,同时学生指出在七年级下册学过的轴对称图形,今天我们要学习平移变换,后面我们还要学习旋转变换,本节课起承上启下的作用,要让学生明确知识的定位.在这里学生各抒己见,用自己所学的知识合情推理并得出自己的结论,养成一个好的数学思维习惯.
活动 二: 实践 探究 交流 新知 【任务一】 平移的定义 问题1.根据上述分析,你能说明什么样的图形运动被称为平移吗 如何定义平移呢 问题2.根据平移的定义,你认为平移应具备哪几个要素 探究结论: 1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.平移不改变图形的形状和大小. 2.平移三要素:(1)几何图形;(2)运动方向;(3)运动距离. 基础训练: 1.平移不改变( ) A.位置 B.形状、大小 C.位置、大小和形状 2.下列可以由图1平移得到的是( ) 【任务二】 平移的性质 如图所示,△ABE沿射线XY的方向平移一定距离成为△CDF.点A,B,E分别平移到了点 ;线段AB,BE,AE分别平移到了 ;∠ABE,∠BAE,∠AEB分别平移到了 . 做一做:如图,四边形ABCD沿某方向平移后成为四边形EFGH,思考: (1)四边形ABCD是沿什么方向平移后成为四边形EFGH的,平移的距离是多少 (2)在上图中,线段AE,BF,CG,DH有怎样的位置关系 (3)每对对应线段之间有怎样的位置关系 (4)图中有哪些相等的线段、相等的角 平移的性质:经过平移, 对应线段 ; 对应角 ; 对应点所连线段 . 基础训练: 如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论错误的是( ) A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF 【任务三】 平移作图 1.如图,经过平移,△ABC的顶点A移到了点D. (1)指出平移的方向和平移的距离; (2)画出平移后的三角形. 2.你还有其他的画法吗 与同伴交流. 3.确定一个图形平移后的位置,需要知道哪些条件 画法一:过点D分别作出与AB,AC平行且相等的线段DE,DF,连接EF,△DEF就是△ABC平移后的图形. 画法二:因为平移后的图形与原图形全等,所以过点B作线段BE,使它与线段AD平行且相等,得到另一个对应点E,用同样的方法得到点C的对应点F,连接DE,EF,FD.△DEF就是△ABC平移后的图形. 确定一个图形平移后的位置,需要以下条件: (1)图形原来的位置.(2)平移的方向.(3)平移的距离. 拓展讲解: 1.平移作图的关键是掌握平移变换的定义和性质,由此作出各个关键点的对应点,顺次连线. 2.对应点的连线属于辅助线,一般画成虚线;对应线段属于平移前后的两个图形的部分,一般画成实线,二者不能混淆. 3.画平行线可以借助推三角尺的方法. 基础训练: 1.如图,在△ABC中,BC= 3cm.将△ABC沿射线BC向右平移4 cm得到△DEF,则BF的长为( ) A.4 cm B.7 cm C.8 cm D.10 cm 2.如图,将周长为8的△ABC沿BC边向右平移2个单位长度得到△DEF,则四边形ABFD的周长为 . 3.如图,在由边长均为1的小正方形组成的方格纸中,△ABC的顶点都在方格纸的格点上,经过平移,△ABC的顶点C移到了点C'的位置. (1)画出平移后的△A'B'C'(点A'与点A对应,点B'与点B对应); (2)指出平移的方向和平移的距离. 让学生根据图片中物体的运动特点,用自己的语言概括出平移的概念和平移的三要素. 巩固对应点、对应线段、对应角的概念,为后续学习做好铺垫. 学生独立思考完成做一做,让学生在观察中总结,在总结中领悟,在领悟中提高,最终得出平移的性质. 学生自己动手画图,按照自己的方法画出平移后的三角形.给学生留出足够的时间来思考,让学生充分交流后总结画图方法以及确定平移后的图形的条件.
活动 三: 开放 训练 体现 应用 【期中、期末链接】 基础训练: 1.(2015-2016)如图,将三角尺ABC的一边AC沿位置固定的直尺推移得到△DEF,下列结论不一定正确的是( ) A.DE∥AB B.四边形ABED是平行四边形 C.AD∥BE D.AD=AB 2.(2016-2017)如图,将线段AB沿箭头方向平移2cm得到线段CD,若AB=3cm,则四边形ABDC的周长为( ) A.8cm B.10cm C.12cm D.20cm 3.(2017-2018)如图,在△ABC中,AB=8,BC=12,∠B=60°,将△ABC沿着射线BC的方向平移得到△A’ B’C’,连接A’C,若BB’=4,则△A’B’C的周长为( ) A.20 B.24 C.36 D.16 4.(2019-2020)如图,△ABC沿线段BA方向平移得到△DEF,若AB=6,AE=2.则平移的距离为( ) A.2 B.4 C.6 D.8 5.(2020-2021)如图,△ABC中,AB=BC=8cm,将△ABC沿BC平移3cm得到△DEF,AC与DE相交于点G,则GE的长为 cm. 能力提升: 6.(2021-2022)如图,Rt△ABC中,∠BAC=90°,将△ABC沿BC方向平移得到△DEF,其中A,B,C的对应点分别是点D,E,F,DE与AC交于点G.若点E是BC的中点,则下列结论中不一定正确的是( ) A.AB=DE B. C.AC与DE互相垂直平分 D.∠DAG=∠DEC 【当堂检测】 基础训练: 1.下列说法中正确的是( ) A.一个图形经过平移后,与原图形成轴对称 B.如果两个图形成轴对称,那么一个图形可由另一个图形经过平移变换得到 C.一个图形经过平移后,它的性质都发生了变化 D.图形的平移由平移的方向和距离决定 2.在以下现象中,属于平移的是( ) ①在荡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动. A.①② B.①③ C.②③ D.②④ 3.如图,大长方形的长是10 cm,宽是8 cm,阴影部分的宽均为2 cm,则空白部分的面积是( ) A.36 cm2 B.40 cm2 C.32 cm2 D.48 cm2 4.如果△ABC沿着北偏东30°的方向移动了2 cm,那么△ABC的边AB上的一点P向 移动了 cm. 5.下列说法:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长不变;④△ABC在平移过程中,面积不变.其中正确的有 (填序号). 能力提升: (2021-2022太原期末) 如图,Rt△ABC中,∠BAC=90°,将△ABC沿BC方向平移得到△DEF,其中A,B,C的对应点分别是点D,E,F,DE与AC交于点G.若点E是BC的中点,则下列结论中不一定正确的是( ) A.AB=DE B. C.AC与DE互相垂直平分 D.∠DAG=∠DEC 通过对期中、期末真题的练习,让学生进一步认识平移,理解平移的基本内涵,理解平移前后两个图形对应点连线平行且相等、对应线段和对应角分别相等的性质. 进一步深化学生对平移的特征的理解,提高学生运用平移特征解决实际问题的能力. 学以致用,课上完成当堂检测,及时了解学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高.
活动 四: 课后 反馈查漏补缺 【课后反馈】 基础达标: 1.下列车标,可看作图案的某一部分经过平移所形成的是( ) A. B. C. D. 2.下列几种运动属于平移的有( ) ①水平运输带上的砖的运动;②电脑的风叶的运动;③升降机上下做机械运动;④足球场上足球的运动. A. 一种 B. 两种 C. 三种 D. 四种 3.下列现象属于平移的是( ) ①打气筒活塞的轮复运动;②电梯的上下运动;③钟摆的摆动;④转动的门;⑤汽车在一条笔直的马路上行走. A. ③ B. ②③ C. ①②④ D. ①②⑤ 4.平移前后两个图形是全等图形,对应点连线( ) A. 平行但不相等 B. 不平行也不相等 C. 平行且相等 D. 不相等 5.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( ) A.平行四边形 B.等腰梯形 C.正六边形 D.圆 6.经过平移,△ABC移到△DEF的位置,如图. 下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF. 其中正确的有( ) A. 0个 B. 1个 C. 2个 D. 3个 7.下列平移图错误的是( ) 能力提升: 8.某景点拟在如图所示的长方形荷塘上架设小桥,若荷塘中小桥的总长为50 m,则荷塘周长为_______m. 9.如图,将直径为的半圆水平向左平移,则半圆所扫过的面积(阴影部分)为( ) A. B. C. D. 拓展延伸: 10.如图所示的4×6正方形网格纸中,小正方形的顶点称为格点,如△ABC的三个顶点都在格点上,平移△ABC,使平移后顶点在格点上,且整个△ABC都在网格纸内,则有_______种不同的平移方法(不同移法但移到同一位置的算同一种). 课后完成课后反馈,让学生能够主动认真完成,同时巩固新课,能够从练习中发现自己的问题,继续深入学习,查漏补缺.
活动 五: 课堂 总结 效果反思 【板书设计】 图形的平移简单应用 框架图式总结,更容易形成知识网络.
【教学反思】 ①[授课流程反思] 本节课通过生活实例,让学生去感受平移,理解平移,为归纳平移的定义及其性质打下基础,使学生深刻感受到数学来源于生活.让学生会用数学的眼光观察世界,会用数学的思维思考世界,会用数学的语言语言表达现实世界. ②[讲授效果反思] 本节课的教学中,通过实例让学生归纳总结平移的定义及平移的性质.通过画图,培养学生的空间几何思维.让学生经历从生活到数学的抽象过程,培养学生的抽象思维能力.通过大量真题,让学生了解本节内容在期中期末的考题,让学生心里有数,最后在通过检测,了解到学生的掌握情况. ③[学生状态反思] 通过学生的练习反馈,了解了大部分学生能够掌握平移,理解平移的基本内涵,同时能够运用平移的性质解题,让学生养成理论联系实际的习惯,发展学生的实践能力. 教学反思,提升自我.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
