5.2.2 平行线的判定课件(27张PPT)华东师大版七年级数学上册
文档属性
| 名称 | 5.2.2 平行线的判定课件(27张PPT)华东师大版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 737.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-04 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第5章 相交线与平行线
5.2 平行线 2.平行线的判定
1.通过画图得到判定直线平行的基本事实,并能由这个基本事实推导出平行线的另外两个判定.
2.会根据平行线的判定进行简单的推理,体会用“∵”“∴”符号的方便.
◎重点:平行线判定的应用.
◎难点:三种判定方法的灵活选用.
如图,木匠师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线a,b.你知道其中的道理吗?今天学行线的判定,同学们就清楚了.
两直线平行的基本事实
阅读课本“同位角相等,两直线平行”前面的内容,通过画图探求这两条线平行的一个基本事实.
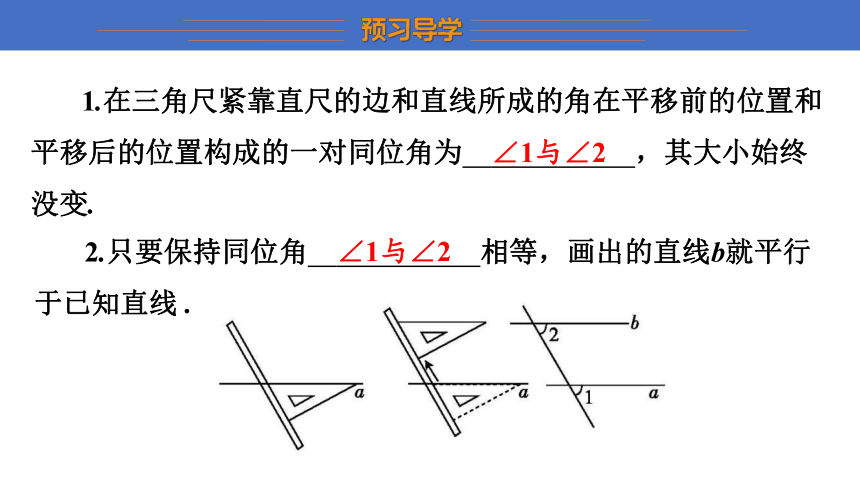
如图所示的方法是上节课画一条直线b与已知直线a平行的方法.
1.在三角尺紧靠直尺的边和直线所成的角在平移前的位置和平移后的位置构成的一对同位角为 ∠1与∠2 ,其大小始终没变.
∠1与∠2
2.只要保持同位角 ∠1与∠2 相等,画出的直线b就平行于已知直线 .
∠1与∠2
归纳总结:
基本事实:两条直线被第三条直线所截,如果 同位角 相等,那么这两条直线 平行 .简单地说,就是同位角 相等 ,两直线平行.
如图(知识点二中),直线a、b被直线c所截,如果∠1=45°,∠4=45°,那么a ∥ b.(填“∥”或“⊥”)
同位角
平行
相等
∥
用内错角相等、同旁内角互补判定两直线平行
阅读课本“同位角相等,两直线平行”后面的内容,学会用两直线平行的基本事实推导后两种判定的方法,并能简单应用.
1.如图,直线a,b被直线c所截.
(1)如果∠2=∠4,那么a∥b对吗?为什么?
对.因为∠2=∠4,∠2=∠1,所以∠1=∠4,所以a∥b.
(2)如果∠3+∠4=180°,那么a∥b对吗?为什么?
对.因为∠3+∠4=180°,∠3+∠1=180°,所以∠1=∠4,所以a∥b.
·导学建议·
在说明“内错角相等,两直线平行”“同旁内角互补,两直线平行”时,要从题目的已知条件出发,得到一组同位角相等,从而用基本事实判断上述两个结论是正确的.也可以让学生用“内错角相等,两直线平行”说明“同旁内角互补,两直线平行”,体会这几个判定之间的关系.
2.由课本“例3”得到“垂直于同一条直线的两条直线 平行 ”,这个结论和上节课得到的“平行于同一条直线的两条直线 平行 ”一样,都可以作为判断两条直线平行的方法.
平
行
平行
·导学建议·
在几个例题的讲解中,注意提醒学生“∵”“∴”的使用方法,其中“∵”开头的是已知条件与以前学过的重要结论,“∴”开头的是已知条件下产生的结果.
归纳总结:1.两条直线被第三条直线所截,如果 内错角 相等,那么这两条直线 平行 .简单地说,就是内错角 相等 ,两直线平行.
内错角
平行
相
等
2.两条直线被第三条直线所截,如果 同旁内角互补 ,那么这两条直线 平行 .简单地说,就是同旁内角 互补 ,两直线平行.
同旁内角互补
平行
互补
如图,一直线截直线AB,CD,得到八个角∠1,∠2,∠3,∠4,∠5,∠6,∠7,∠8.请你根据要求填空.
(1)∵∠3 =∠5(已知),∴ AB ∥ CD .( 内错角相等,两直线平行 )
AB
CD
内错角相
等,两直线平行
(2)∵∠4+∠5=180°(已知),∴ AB ∥ CD .( 同旁内角互补,两直线平行 )
AB
CD
同
旁内角互补,两直线平行
·导学建议·
两直线平行的基本事实让学生由画图得到即可,不必要解释过多,另外两种方法的推导,应引导学生逐步学会说理,并结合后面的例题,给出过程,培养学生几何说理的能力.预习部分可以用15分钟左右的时间完成.
平行线判定的直接应用
1.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( D )
A.∠2=∠4 B.∠1+∠4=180°
C.∠5=∠4 D.∠1=∠3
D
【变式演练】如图,E是AD延长线上一点,∠B=30°,∠C=120°.如果添加一个条件,使BC∥AD,那么可添加的条件为 ∠1=30°或∠2=120° .(只填一个即可)
∠1=30°或∠2=120°
用平行线的判定进行说理
2.如图,CE⊥DG于点C,∠BAF=50°,∠ACE=140°,CD与AB平行吗?为什么?
解:AB∥CD.理由如下:∵CE⊥DG,∴∠ECG=90°.∵∠ACE=140°,∴∠ACG=50°.∵∠BAF=50°,∴∠BAF=∠ACG,∴AB∥CD.
【变式演练】如图,AE与CD交于点O,∠A=40°,OC=OE,∠C=20°,求证:AB∥CD.
证明:∵OC=OE,∴∠E=∠C=20°,∴∠DOE=∠C+∠E=40°.∵∠A=40°,∴∠A=∠DOE,∴AB∥CD.
3.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C,求证:DE∥BC.
证明:∵∠1+∠DHE=180°,∠1+∠2=180°,∴∠DHE=∠2,∴DH∥AC.∴∠3=∠AED,
∵∠3=∠C,∴∠C=∠AED,∴DE∥BC.
【方法归纳交流】符号“∵”“∴”分别表示 “因为”“所以” ,括号内所写的,就是括号前这一结论成立的依据.“对顶角相等”“等量代换”“等式的性质”常常作为推理的依据.
“因
为”“所以”
利用平行线的判定解决实际问题
4.在铺设铁轨时,两条直轨必须是互相平行的.如图,已知∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直线是否平行?为什么?
解:(1)通过度量∠3的度数,若满足∠2+∠3=180°,根据“同旁内角互补,两直线平行”就可以验证这个结论;(2)通过度量∠4的度数,若满足∠2=∠4,根据“同位角相等,两直线平行”就可以验证这个结论;(3)通过度量∠5的度数,若满足∠2=∠5,根据“内错角相等,两直线平行”就可以验证这个结论.
判断两直线是否平行,一般是从角的关系入手,找角的相等或互补关系.在解答时,还要逐渐培养学生说理的能力,会用数学语言解答问题.合作探究部分可以用20分钟左右的时间完成,备选问题根据学情选用.
·导学建议·
如图,∠ABC=∠DEF,∠E+∠AME=180°,AB,EF相交于点M,试判断BC,EF是否平行,并说明理由.
解:∵∠DEF+∠AME=180°,∠ABC=∠DEF(已知),
∴∠ABC+∠AME=180°(等量代换).
∵∠BME+∠AME=180°(平角定义),
∴∠ABC=∠BME(同角的补角相等),
∴BC∥EF(内错角相等,两直线平行).
第5章 相交线与平行线
5.2 平行线 2.平行线的判定
1.通过画图得到判定直线平行的基本事实,并能由这个基本事实推导出平行线的另外两个判定.
2.会根据平行线的判定进行简单的推理,体会用“∵”“∴”符号的方便.
◎重点:平行线判定的应用.
◎难点:三种判定方法的灵活选用.
如图,木匠师傅用角尺画出工件边缘的两条垂线,就可以在工件上找出两条平行线a,b.你知道其中的道理吗?今天学行线的判定,同学们就清楚了.
两直线平行的基本事实
阅读课本“同位角相等,两直线平行”前面的内容,通过画图探求这两条线平行的一个基本事实.
如图所示的方法是上节课画一条直线b与已知直线a平行的方法.
1.在三角尺紧靠直尺的边和直线所成的角在平移前的位置和平移后的位置构成的一对同位角为 ∠1与∠2 ,其大小始终没变.
∠1与∠2
2.只要保持同位角 ∠1与∠2 相等,画出的直线b就平行于已知直线 .
∠1与∠2
归纳总结:
基本事实:两条直线被第三条直线所截,如果 同位角 相等,那么这两条直线 平行 .简单地说,就是同位角 相等 ,两直线平行.
如图(知识点二中),直线a、b被直线c所截,如果∠1=45°,∠4=45°,那么a ∥ b.(填“∥”或“⊥”)
同位角
平行
相等
∥
用内错角相等、同旁内角互补判定两直线平行
阅读课本“同位角相等,两直线平行”后面的内容,学会用两直线平行的基本事实推导后两种判定的方法,并能简单应用.
1.如图,直线a,b被直线c所截.
(1)如果∠2=∠4,那么a∥b对吗?为什么?
对.因为∠2=∠4,∠2=∠1,所以∠1=∠4,所以a∥b.
(2)如果∠3+∠4=180°,那么a∥b对吗?为什么?
对.因为∠3+∠4=180°,∠3+∠1=180°,所以∠1=∠4,所以a∥b.
·导学建议·
在说明“内错角相等,两直线平行”“同旁内角互补,两直线平行”时,要从题目的已知条件出发,得到一组同位角相等,从而用基本事实判断上述两个结论是正确的.也可以让学生用“内错角相等,两直线平行”说明“同旁内角互补,两直线平行”,体会这几个判定之间的关系.
2.由课本“例3”得到“垂直于同一条直线的两条直线 平行 ”,这个结论和上节课得到的“平行于同一条直线的两条直线 平行 ”一样,都可以作为判断两条直线平行的方法.
平
行
平行
·导学建议·
在几个例题的讲解中,注意提醒学生“∵”“∴”的使用方法,其中“∵”开头的是已知条件与以前学过的重要结论,“∴”开头的是已知条件下产生的结果.
归纳总结:1.两条直线被第三条直线所截,如果 内错角 相等,那么这两条直线 平行 .简单地说,就是内错角 相等 ,两直线平行.
内错角
平行
相
等
2.两条直线被第三条直线所截,如果 同旁内角互补 ,那么这两条直线 平行 .简单地说,就是同旁内角 互补 ,两直线平行.
同旁内角互补
平行
互补
如图,一直线截直线AB,CD,得到八个角∠1,∠2,∠3,∠4,∠5,∠6,∠7,∠8.请你根据要求填空.
(1)∵∠3 =∠5(已知),∴ AB ∥ CD .( 内错角相等,两直线平行 )
AB
CD
内错角相
等,两直线平行
(2)∵∠4+∠5=180°(已知),∴ AB ∥ CD .( 同旁内角互补,两直线平行 )
AB
CD
同
旁内角互补,两直线平行
·导学建议·
两直线平行的基本事实让学生由画图得到即可,不必要解释过多,另外两种方法的推导,应引导学生逐步学会说理,并结合后面的例题,给出过程,培养学生几何说理的能力.预习部分可以用15分钟左右的时间完成.
平行线判定的直接应用
1.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b的是( D )
A.∠2=∠4 B.∠1+∠4=180°
C.∠5=∠4 D.∠1=∠3
D
【变式演练】如图,E是AD延长线上一点,∠B=30°,∠C=120°.如果添加一个条件,使BC∥AD,那么可添加的条件为 ∠1=30°或∠2=120° .(只填一个即可)
∠1=30°或∠2=120°
用平行线的判定进行说理
2.如图,CE⊥DG于点C,∠BAF=50°,∠ACE=140°,CD与AB平行吗?为什么?
解:AB∥CD.理由如下:∵CE⊥DG,∴∠ECG=90°.∵∠ACE=140°,∴∠ACG=50°.∵∠BAF=50°,∴∠BAF=∠ACG,∴AB∥CD.
【变式演练】如图,AE与CD交于点O,∠A=40°,OC=OE,∠C=20°,求证:AB∥CD.
证明:∵OC=OE,∴∠E=∠C=20°,∴∠DOE=∠C+∠E=40°.∵∠A=40°,∴∠A=∠DOE,∴AB∥CD.
3.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C,求证:DE∥BC.
证明:∵∠1+∠DHE=180°,∠1+∠2=180°,∴∠DHE=∠2,∴DH∥AC.∴∠3=∠AED,
∵∠3=∠C,∴∠C=∠AED,∴DE∥BC.
【方法归纳交流】符号“∵”“∴”分别表示 “因为”“所以” ,括号内所写的,就是括号前这一结论成立的依据.“对顶角相等”“等量代换”“等式的性质”常常作为推理的依据.
“因
为”“所以”
利用平行线的判定解决实际问题
4.在铺设铁轨时,两条直轨必须是互相平行的.如图,已知∠2是直角,那么再度量图中已标出的哪个角,就可以判断两条直线是否平行?为什么?
解:(1)通过度量∠3的度数,若满足∠2+∠3=180°,根据“同旁内角互补,两直线平行”就可以验证这个结论;(2)通过度量∠4的度数,若满足∠2=∠4,根据“同位角相等,两直线平行”就可以验证这个结论;(3)通过度量∠5的度数,若满足∠2=∠5,根据“内错角相等,两直线平行”就可以验证这个结论.
判断两直线是否平行,一般是从角的关系入手,找角的相等或互补关系.在解答时,还要逐渐培养学生说理的能力,会用数学语言解答问题.合作探究部分可以用20分钟左右的时间完成,备选问题根据学情选用.
·导学建议·
如图,∠ABC=∠DEF,∠E+∠AME=180°,AB,EF相交于点M,试判断BC,EF是否平行,并说明理由.
解:∵∠DEF+∠AME=180°,∠ABC=∠DEF(已知),
∴∠ABC+∠AME=180°(等量代换).
∵∠BME+∠AME=180°(平角定义),
∴∠ABC=∠BME(同角的补角相等),
∴BC∥EF(内错角相等,两直线平行).
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
