26.3 实践与探索(1)课件(共18张PPT) 华东师大版九年级数学下册
文档属性
| 名称 | 26.3 实践与探索(1)课件(共18张PPT) 华东师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 542.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 08:12:54 | ||
图片预览




文档简介
(共18张PPT)
26.3 实践与探索
第1课时
第26章 二次函数
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.会建立二次函数模型,解决与之相关的运动物体中的实际问题.
2.会运用二次函数模型解决销售中最大利润等问题,体会运用数学模型选择最优化方案.
3.体会数学建模的思想,感受数学的实际应用价值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
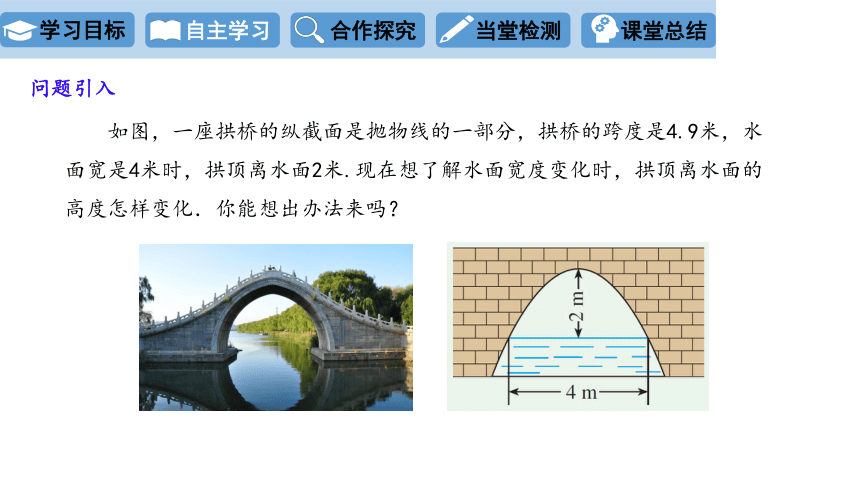
问题引入
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
思考1:这是什么样的函数呢?
拱桥的纵截面是抛物线,所以应当是个二次函数
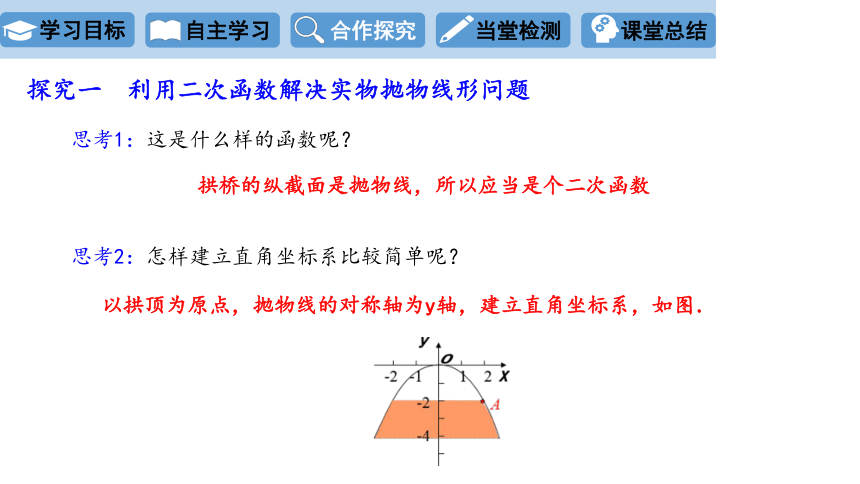
思考2:怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
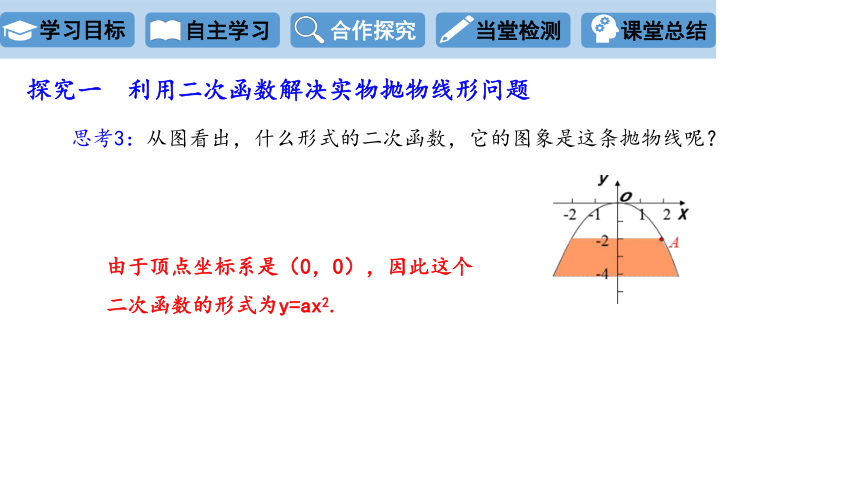
思考3:从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0,0),因此这个二次函数的形式为y=ax2.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考4:如何确定a是多少?
x
O
y
-2
-4
2
1
-2
-1
A
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
解得
因此, ,其中|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
思考5:现在你能求出水面宽3米时,拱顶离水面高多少米吗?
水面宽3m时,
从而
因此拱顶离水面高1.125m.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:抛物线形问题的一般解题步骤:
(1)建立适当的平面直角系,并将已知条件转化为点的坐标;
(2)合理地设出所求的函数的表达式,并代入已知条件或点的坐标,
求出关系式;
(3)利用关系式求解实际问题.
探究一 利用二次函数解决实物抛物线形问题
知识要点
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的图象和性质求解
实际问题的解
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
O
A
C
D
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题提出:某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
分析:销售利润问题中常用的数量关系:
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究1:
①每件涨价x元,则每星期售出商品的利润y元,填空:
涨价销售
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即定价65元时,最大利润是6250元.
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究2:
①每件降价x元,则每星期售出商品的利润y元,填空:
降价销售
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
20
300
20-x
300+20x
y=(20-x)(300+20x)
建立函数关系式:y=(20-x)(300+20x),
即:y=-20x2+100x+6000.
6000
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
当 时,
即定价57.5元时,最大利润是6125元.
即:y=-20x2+100x+6000,
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 利用二次函数解决商品利润问题
求解最大利润问题的一般步骤:
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
2.某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
合作探究
当堂检测
学习目标
课堂总结
自主学习
y=(160+10x)(120-6x)
解:设每间客房的日租金提高10x元,则每天客房出租数会减少6x间,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入最高,最大收入为19440.
=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
这时每间客房的日租金为160+10×2=180(元).
合作探究
当堂检测
学习目标
课堂总结
自主学习
转化
回归
(二次函数的图象和性质)
(实物中的抛物线形问题)
实际问题
数学模型
26.3 实践与探索
第1课时
第26章 二次函数
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.会建立二次函数模型,解决与之相关的运动物体中的实际问题.
2.会运用二次函数模型解决销售中最大利润等问题,体会运用数学模型选择最优化方案.
3.体会数学建模的思想,感受数学的实际应用价值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题引入
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
思考1:这是什么样的函数呢?
拱桥的纵截面是抛物线,所以应当是个二次函数
思考2:怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考3:从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
由于顶点坐标系是(0,0),因此这个二次函数的形式为y=ax2.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考4:如何确定a是多少?
x
O
y
-2
-4
2
1
-2
-1
A
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
解得
因此, ,其中|x|是水面宽度的一半,y是拱顶离水面高度的相反数,这样我们就可以了解到水面宽度变化时,拱顶离水面高度怎样变化.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
思考5:现在你能求出水面宽3米时,拱顶离水面高多少米吗?
水面宽3m时,
从而
因此拱顶离水面高1.125m.
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳:抛物线形问题的一般解题步骤:
(1)建立适当的平面直角系,并将已知条件转化为点的坐标;
(2)合理地设出所求的函数的表达式,并代入已知条件或点的坐标,
求出关系式;
(3)利用关系式求解实际问题.
探究一 利用二次函数解决实物抛物线形问题
知识要点
建立二次函数模型解决实际问题的基本步骤是什么?
实际问题
建立二次函数模型
利用二次函数的图象和性质求解
实际问题的解
探究一 利用二次函数解决实物抛物线形问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
O
A
C
D
B
y
x
20 m
h
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题提出:某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
分析:销售利润问题中常用的数量关系:
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究1:
①每件涨价x元,则每星期售出商品的利润y元,填空:
涨价销售
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即定价65元时,最大利润是6250元.
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究2:
①每件降价x元,则每星期售出商品的利润y元,填空:
降价销售
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
20
300
20-x
300+20x
y=(20-x)(300+20x)
建立函数关系式:y=(20-x)(300+20x),
即:y=-20x2+100x+6000.
6000
探究二 利用二次函数解决商品利润问题
合作探究
当堂检测
学习目标
课堂总结
自主学习
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
当 时,
即定价57.5元时,最大利润是6125元.
即:y=-20x2+100x+6000,
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 利用二次函数解决商品利润问题
求解最大利润问题的一般步骤:
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
2.某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
合作探究
当堂检测
学习目标
课堂总结
自主学习
y=(160+10x)(120-6x)
解:设每间客房的日租金提高10x元,则每天客房出租数会减少6x间,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入最高,最大收入为19440.
=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
这时每间客房的日租金为160+10×2=180(元).
合作探究
当堂检测
学习目标
课堂总结
自主学习
转化
回归
(二次函数的图象和性质)
(实物中的抛物线形问题)
实际问题
数学模型
