12.3 等腰三角形课时练(人教新课标八年级上)
文档属性
| 名称 | 12.3 等腰三角形课时练(人教新课标八年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 129.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学:12.3 等腰三角形课时练(人教新课标八年级上)
第一课时
1. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的
距离是( )
A.3 B.4 C.5 D.6
&2. 在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
&3. 如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12 cm,AC=5cm,△ABC的周长是__________cm
4. 如图所示是一个风筝骨架.为使风筝平衡,须使∠AOP=∠BOP.我们已知PC⊥OA,PD⊥OB,那么PC和PD满足 条件,才能保证OP为∠AOB角平分线
&5. 如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.
求证:AD平分∠BAC.
6.已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
且BC=DC.你能说明BE与DF相等吗?
※7. 已知:如图,AB=AC=12 cm,AB的垂直平分线分别交
AC、AB于D、E,△ABD的周长等于29 cm,
求DC的长.
#8. 如图所示,一辆汽车在笔直的公路AB上由A向B行驶,
M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个
位置时,与村庄M,N的距离相等
第二课时
#1.下列图形中,不一定是轴对称图形的是 ( )
A.等腰三角形 B.等腰直角三角形
C.等边三角形 D.直角三角形
&2. 若等腰三角形的顶角的外角是80°,
那么它的底角是____________.
※3. 如图,B、D、F在AN上,C、E在AM上,
且AB=BC=CD,EC=ED=EF,∠A=20°,
则∠FEM度数是 .
&4. 在△ABC中,AB=AC,∠A=36°,
角平分线BE与CD相交于点F,
那么图中等腰三角形有 ( )
A.6个 B.7个
C.8个 D.9个
#5. 如图,已知AC=CD=DA=CB=DE,则此图中共有 ______ 个等腰三角形.
※6..如图所示,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN经过点O,若AB=12,AC=18,那么△AMN的周长是
&7. 已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC(如图).
求证:AB=AC.
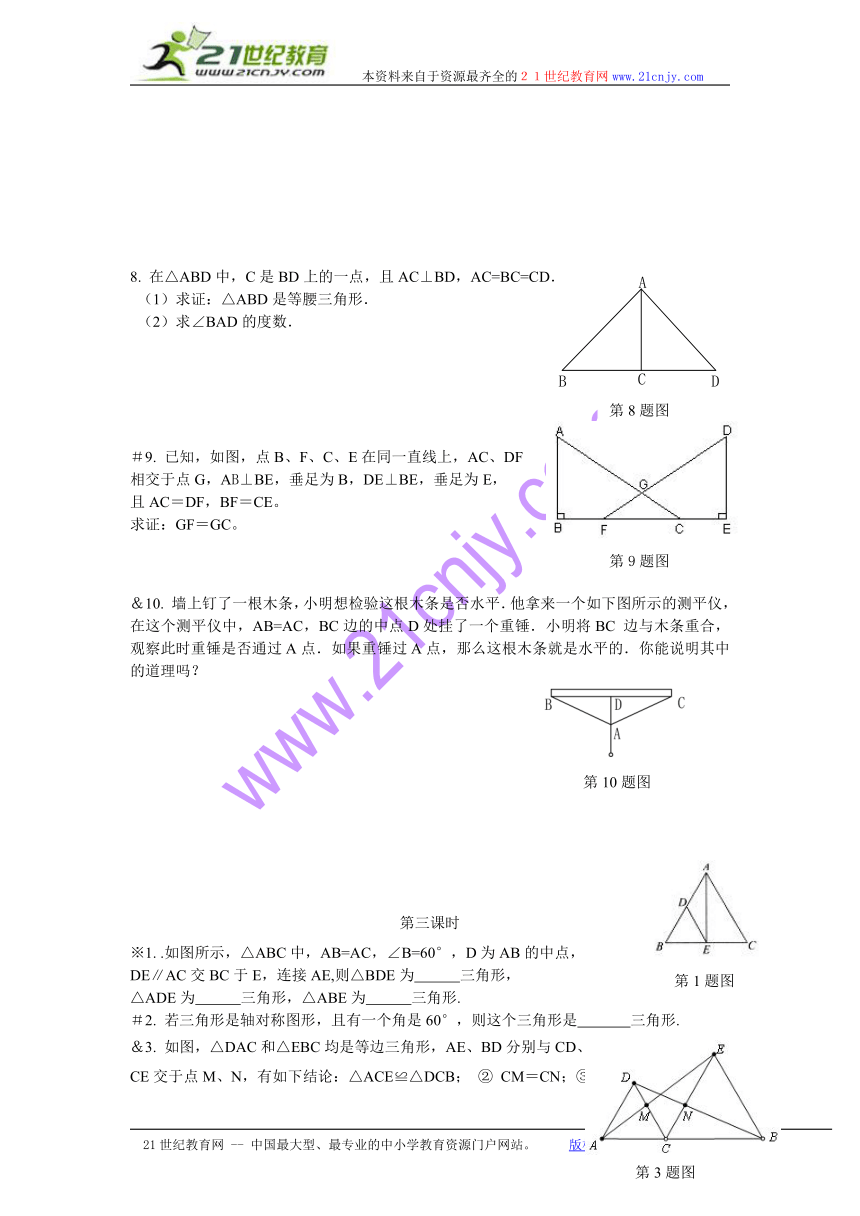
8. 在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形.
(2)求∠BAD的度数.
#9. 已知,如图,点B、F、C、E在同一直线上,AC、DF
相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,
且AC=DF,BF=CE。
求证:GF=GC。
&10. 墙上钉了一根木条,小明想检验这根木条是否水平.他拿来一个如下图所示的测平仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤.小明将BC边与木条重合,观察此时重锤是否通过A点.如果重锤过A点,那么这根木条就是水平的.你能说明其中的道理吗?
第三课时
※1. .如图所示,△ABC中,AB=AC,∠B=60°,D为AB的中点,
DE∥AC交BC于E,连接AE,则△BDE为 三角形,
△ADE为 三角形,△ABE为 三角形.
#2. 若三角形是轴对称图形,且有一个角是60°,则这个三角形是 三角形.
&3. 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、
CE交于点M、N,有如下结论:△ACE≌△DCB; ② CM=CN;③ AC=DN。其中,
正确结论的个数是( )
A. 3个 B.2个 C.1个 D.0个
※4. △ABC中,若AC=10,则BC= .
※5. 如图,中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,
则CD= ___ 。
&6. 如图所示,C、D是两个村庄,分别位于一个湖的南、北两端A和
B的正东方向上,且D位于C的北偏东60°方向上,CD=6,
则AB= .
#7. 一个直角三角形房梁如图所示,其中BC⊥AC,∠BAC=30°,
AB=10cm,CB1⊥AB,B1C⊥AC1,垂足分别是B1、C1,
那么BC的长是多少?
#8. 已知:如图,在Rt△ABC中,∠C=90°,BC=AB.
求证:∠BAC=30°.
9. 如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.
在图(1)中, 点P是边BC的中点,此时h3=0,可得结论:.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中, h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60o, RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为: ;图(4)与图(6)中的等式有何关系?
第一课时答案:
1. A,提示:过P 点作PF⊥AB交AB于F点,根据角平分线定理得PE=PF=3,故A;2.B;
3.17
4.PC=PD;
5. 证明:在△BDF和△CDE中
∴△BDF≌△CDE,∴DF=DE
∴D在∠A的平分线上,∴AD平分∠BAC.
6.相等:理由:
∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,∴CF=CE,
在△CFD和△CEB中,,∴△CFD≌△CEB
∴BE=DF.
7.解:∵AB的垂直平分线分别交AC、AB于D、E,∴AD=BD,又∵AB+AD+BD=29 cm,AB=12 cm,∴AD=8 cm,又∵AC=12 cm,AC=AD+DC,∴DC=4 cm;
8. 作法:(1)连接MN;
(2)作线段MN的垂直平分线,
交直线AB于C点,则C点即为所求.
第二课时答案:
1.D;2.40°,提示:等腰三角形的顶角是100°,则底角为(180°-100°)=40°;3.100°,提示:根据等边对等角和三角形的外角定理得∠FEM=∠A+∠EFA=20°+80°=100°;4.C;5.4;6. .30;
7. 证明:∵AD∥BC,∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
8. (1)证明:∵AC⊥BD,∴∠ACB=∠ACD=90°.
又∵AC=AC,BC=CD,∴△ACB≌△ACD(SAS).
∴AB=AD(全等三角形的对应边相等). ∴△ABD是等腰三角形.
(2)解:由(1)可知AB=AD, ∴∠B=∠D.又∵AC=BC, ∴∠B=∠BAC,
AC=CD.∴∠D=∠DAC(等边对等角).
在△ABD中,∠B+∠D+∠BAC+∠DAC=180°,
∴2(∠BAC+∠DAC)=180°. ∴∠BAC+∠DAC=90°,
即∠BAD=90°.
9. 证明:∵BF=CE ∴BF+FC=CE+FC,即BC=EF
又∵AB⊥BE,DE⊥BE ∴∠B=∠E=900
又∵AC=DF ∴△ABC≌△DEF,∴∠ACB=∠DFE
∴GF=GC
10.根据等腰三角形“三线合一”的性质,等腰三角形ABC底边BC上的中线DA应垂直于底边BC(即木条),如果重锤过点A,说明直线AD垂直于水平线,那么木条就是水平的.根据是平面内过直线外一点有且只有一条直线与已知直线垂直.
第三课时答案:
1. 等边,等腰,直角;2.等边;3.B;4.5,提示:根据在直角三角形中,30°所对的直角边等于斜边的一半;5. 3;6.3,提示:过C点作垂线,转化到直角三角形和矩形解决;
7. 解:在Rt△ABC中,∠CAB=30°,AB=10cm. ∴BC=AB=5cm.
∵CB1⊥AB, ∴∠B+∠BCB1=90°. 又∵∠A+∠B=90°,∴∠BCB1=∠A=30°.
在Rt△ACB1中,BB1=BC=2.5cm. ∴AB1=AB-BB1=10-2.5=7.5(cm).
∴在Rt△AB1C1中,∠A=30°.
∴B1C1=AB1=×7.5=3.75(cm).
8. 证明:延长BC到D,使CD=BC,连结AD.
∵∠ACB=90°,∴∠ACD=90°.
又∵AC=AC,∴△ACB≌△ACD(SAS).
∴AB=AD.∵CD=BC, ∴BC=BD. 又∵BC=AB,
∴AB=BD. ∴AB=AD=BD, 即△ABD为等边三角形.
∴∠B=60°.
在Rt△ABC中,∠BAC=30°.
9. 解:(1)图②—⑤ 中的关系依次是:
h1+h2+h3=h; h1-h2+h3=h; h1+h2+h3=h; h1+h2-h3=h.
(2)图②中,h1+h2+h3=h.
证明:连结AP, 则SΔAPB+SΔAPC=SΔABC.
∴ .
又 h3=0,AB=AC=BC, ∴ h1+h2+h3==h.
(3)证明:图④中,h1+h2+h3=h.
过点P作RS∥BC与边AB、AC相交于R、S.
在△ARS中,由图②中结论知:h1+h2+0=h-h3.
∴ h1+h2+h3=h.
说明:(2)与(3)问,通过作辅助线,利用证全等三角形的方法类似给分.
(4)h1+h3+h4= .
第2题图
第1题图
第3题图
第4题图
第5题图
A
B
C
D
E
F
1
2
第6题图
第7题图
第8题图
第4题图
第6题图
第5题图
第7题图
第8题图
第9题图
第10题图
第1题图
第3题图
第5题图
第6题图
第7题图
第8题图
F
A
B
C
D
E
P
M
(4)
A
B
C
D
E
P
M
(3)
A
B
C
D
E
P
M
(2)
A
B
C
D
E
M(P)
(1)
A
B
C
D
E
P
M
(5)
第9题图
F
A
B
C
D
E
P
M
(6)
R
S
第5题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学:12.3 等腰三角形课时练(人教新课标八年级上)
第一课时
1. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=3,则点P到AB的
距离是( )
A.3 B.4 C.5 D.6
&2. 在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
&3. 如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12 cm,AC=5cm,△ABC的周长是__________cm
4. 如图所示是一个风筝骨架.为使风筝平衡,须使∠AOP=∠BOP.我们已知PC⊥OA,PD⊥OB,那么PC和PD满足 条件,才能保证OP为∠AOB角平分线
&5. 如图所示,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.
求证:AD平分∠BAC.
6.已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
且BC=DC.你能说明BE与DF相等吗?
※7. 已知:如图,AB=AC=12 cm,AB的垂直平分线分别交
AC、AB于D、E,△ABD的周长等于29 cm,
求DC的长.
#8. 如图所示,一辆汽车在笔直的公路AB上由A向B行驶,
M,N分别是位于公路AB两侧的村庄,当汽车行驶到哪个
位置时,与村庄M,N的距离相等
第二课时
#1.下列图形中,不一定是轴对称图形的是 ( )
A.等腰三角形 B.等腰直角三角形
C.等边三角形 D.直角三角形
&2. 若等腰三角形的顶角的外角是80°,
那么它的底角是____________.
※3. 如图,B、D、F在AN上,C、E在AM上,
且AB=BC=CD,EC=ED=EF,∠A=20°,
则∠FEM度数是 .
&4. 在△ABC中,AB=AC,∠A=36°,
角平分线BE与CD相交于点F,
那么图中等腰三角形有 ( )
A.6个 B.7个
C.8个 D.9个
#5. 如图,已知AC=CD=DA=CB=DE,则此图中共有 ______ 个等腰三角形.
※6..如图所示,在△ABC中,BO平分∠ABC,CO平分∠ACB,MN∥BC,MN经过点O,若AB=12,AC=18,那么△AMN的周长是
&7. 已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC(如图).
求证:AB=AC.
8. 在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形.
(2)求∠BAD的度数.
#9. 已知,如图,点B、F、C、E在同一直线上,AC、DF
相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,
且AC=DF,BF=CE。
求证:GF=GC。
&10. 墙上钉了一根木条,小明想检验这根木条是否水平.他拿来一个如下图所示的测平仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤.小明将BC边与木条重合,观察此时重锤是否通过A点.如果重锤过A点,那么这根木条就是水平的.你能说明其中的道理吗?
第三课时
※1. .如图所示,△ABC中,AB=AC,∠B=60°,D为AB的中点,
DE∥AC交BC于E,连接AE,则△BDE为 三角形,
△ADE为 三角形,△ABE为 三角形.
#2. 若三角形是轴对称图形,且有一个角是60°,则这个三角形是 三角形.
&3. 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、
CE交于点M、N,有如下结论:△ACE≌△DCB; ② CM=CN;③ AC=DN。其中,
正确结论的个数是( )
A. 3个 B.2个 C.1个 D.0个
※4. △ABC中,若AC=10,则BC= .
※5. 如图,中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,
则CD= ___ 。
&6. 如图所示,C、D是两个村庄,分别位于一个湖的南、北两端A和
B的正东方向上,且D位于C的北偏东60°方向上,CD=6,
则AB= .
#7. 一个直角三角形房梁如图所示,其中BC⊥AC,∠BAC=30°,
AB=10cm,CB1⊥AB,B1C⊥AC1,垂足分别是B1、C1,
那么BC的长是多少?
#8. 已知:如图,在Rt△ABC中,∠C=90°,BC=AB.
求证:∠BAC=30°.
9. 如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.
在图(1)中, 点P是边BC的中点,此时h3=0,可得结论:.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中, h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60o, RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为: ;图(4)与图(6)中的等式有何关系?
第一课时答案:
1. A,提示:过P 点作PF⊥AB交AB于F点,根据角平分线定理得PE=PF=3,故A;2.B;
3.17
4.PC=PD;
5. 证明:在△BDF和△CDE中
∴△BDF≌△CDE,∴DF=DE
∴D在∠A的平分线上,∴AD平分∠BAC.
6.相等:理由:
∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,∴CF=CE,
在△CFD和△CEB中,,∴△CFD≌△CEB
∴BE=DF.
7.解:∵AB的垂直平分线分别交AC、AB于D、E,∴AD=BD,又∵AB+AD+BD=29 cm,AB=12 cm,∴AD=8 cm,又∵AC=12 cm,AC=AD+DC,∴DC=4 cm;
8. 作法:(1)连接MN;
(2)作线段MN的垂直平分线,
交直线AB于C点,则C点即为所求.
第二课时答案:
1.D;2.40°,提示:等腰三角形的顶角是100°,则底角为(180°-100°)=40°;3.100°,提示:根据等边对等角和三角形的外角定理得∠FEM=∠A+∠EFA=20°+80°=100°;4.C;5.4;6. .30;
7. 证明:∵AD∥BC,∴∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边).
8. (1)证明:∵AC⊥BD,∴∠ACB=∠ACD=90°.
又∵AC=AC,BC=CD,∴△ACB≌△ACD(SAS).
∴AB=AD(全等三角形的对应边相等). ∴△ABD是等腰三角形.
(2)解:由(1)可知AB=AD, ∴∠B=∠D.又∵AC=BC, ∴∠B=∠BAC,
AC=CD.∴∠D=∠DAC(等边对等角).
在△ABD中,∠B+∠D+∠BAC+∠DAC=180°,
∴2(∠BAC+∠DAC)=180°. ∴∠BAC+∠DAC=90°,
即∠BAD=90°.
9. 证明:∵BF=CE ∴BF+FC=CE+FC,即BC=EF
又∵AB⊥BE,DE⊥BE ∴∠B=∠E=900
又∵AC=DF ∴△ABC≌△DEF,∴∠ACB=∠DFE
∴GF=GC
10.根据等腰三角形“三线合一”的性质,等腰三角形ABC底边BC上的中线DA应垂直于底边BC(即木条),如果重锤过点A,说明直线AD垂直于水平线,那么木条就是水平的.根据是平面内过直线外一点有且只有一条直线与已知直线垂直.
第三课时答案:
1. 等边,等腰,直角;2.等边;3.B;4.5,提示:根据在直角三角形中,30°所对的直角边等于斜边的一半;5. 3;6.3,提示:过C点作垂线,转化到直角三角形和矩形解决;
7. 解:在Rt△ABC中,∠CAB=30°,AB=10cm. ∴BC=AB=5cm.
∵CB1⊥AB, ∴∠B+∠BCB1=90°. 又∵∠A+∠B=90°,∴∠BCB1=∠A=30°.
在Rt△ACB1中,BB1=BC=2.5cm. ∴AB1=AB-BB1=10-2.5=7.5(cm).
∴在Rt△AB1C1中,∠A=30°.
∴B1C1=AB1=×7.5=3.75(cm).
8. 证明:延长BC到D,使CD=BC,连结AD.
∵∠ACB=90°,∴∠ACD=90°.
又∵AC=AC,∴△ACB≌△ACD(SAS).
∴AB=AD.∵CD=BC, ∴BC=BD. 又∵BC=AB,
∴AB=BD. ∴AB=AD=BD, 即△ABD为等边三角形.
∴∠B=60°.
在Rt△ABC中,∠BAC=30°.
9. 解:(1)图②—⑤ 中的关系依次是:
h1+h2+h3=h; h1-h2+h3=h; h1+h2+h3=h; h1+h2-h3=h.
(2)图②中,h1+h2+h3=h.
证明:连结AP, 则SΔAPB+SΔAPC=SΔABC.
∴ .
又 h3=0,AB=AC=BC, ∴ h1+h2+h3==h.
(3)证明:图④中,h1+h2+h3=h.
过点P作RS∥BC与边AB、AC相交于R、S.
在△ARS中,由图②中结论知:h1+h2+0=h-h3.
∴ h1+h2+h3=h.
说明:(2)与(3)问,通过作辅助线,利用证全等三角形的方法类似给分.
(4)h1+h3+h4= .
第2题图
第1题图
第3题图
第4题图
第5题图
A
B
C
D
E
F
1
2
第6题图
第7题图
第8题图
第4题图
第6题图
第5题图
第7题图
第8题图
第9题图
第10题图
第1题图
第3题图
第5题图
第6题图
第7题图
第8题图
F
A
B
C
D
E
P
M
(4)
A
B
C
D
E
P
M
(3)
A
B
C
D
E
P
M
(2)
A
B
C
D
E
M(P)
(1)
A
B
C
D
E
P
M
(5)
第9题图
F
A
B
C
D
E
P
M
(6)
R
S
第5题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
