11.1全等三角形-11.2三角形全等的判定课时练(人教新课标八年级上)
文档属性
| 名称 | 11.1全等三角形-11.2三角形全等的判定课时练(人教新课标八年级上) | 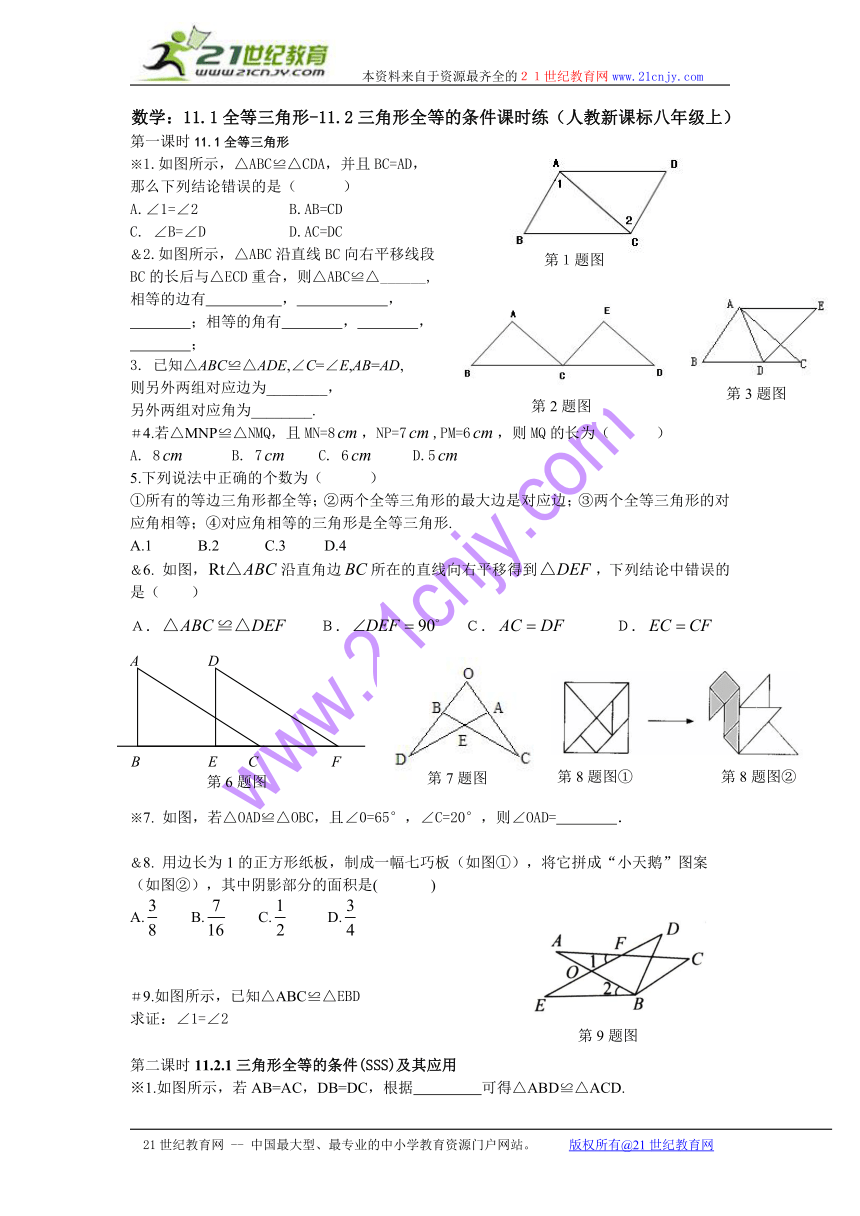 | |
| 格式 | rar | ||
| 文件大小 | 228.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 22:02:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学:11.1全等三角形-11.2三角形全等的条件课时练(人教新课标八年级上)
第一课时11.1全等三角形
※1.如图所示,△ABC≌△CDA,并且BC=AD,
那么下列结论错误的是( )
A.∠1=∠2 B.AB=CD
C. ∠B=∠D D.AC=DC
&2.如图所示,△ABC沿直线BC向右平移线段
BC的长后与△ECD重合,则△ABC≌△______,
相等的边有 , ,
;相等的角有 , ,
;
3. 已知△ABC≌△ADE,∠C=∠E,AB=AD,
则另外两组对应边为________,
另外两组对应角为________.
#4.若△MNP≌△NMQ,且MN=8,NP=7,PM=6,则MQ的长为( )
A. 8 B. 7 C. 6 D.5
5.下列说法中正确的个数为( )
①所有的等边三角形都全等;②两个全等三角形的最大边是对应边;③两个全等三角形的对应角相等;④对应角相等的三角形是全等三角形.
A.1 B.2 C.3 D.4
&6. 如图,沿直角边所在的直线向右平移得到,下列结论中错误的是( )
A. B. C. D.
※7. 如图,若△OAD≌△OBC,且∠0=65°,∠C=20°,则∠OAD= .
&8. 用边长为1的正方形纸板,制成一幅七巧板(如图①),将它拼成“小天鹅”图案
(如图②),其中阴影部分的面积是( )
A. B. C. D.
#9.如图所示,已知△ABC≌△EBD
求证:∠1=∠2
第二课时11.2.1三角形全等的条件(SSS)及其应用
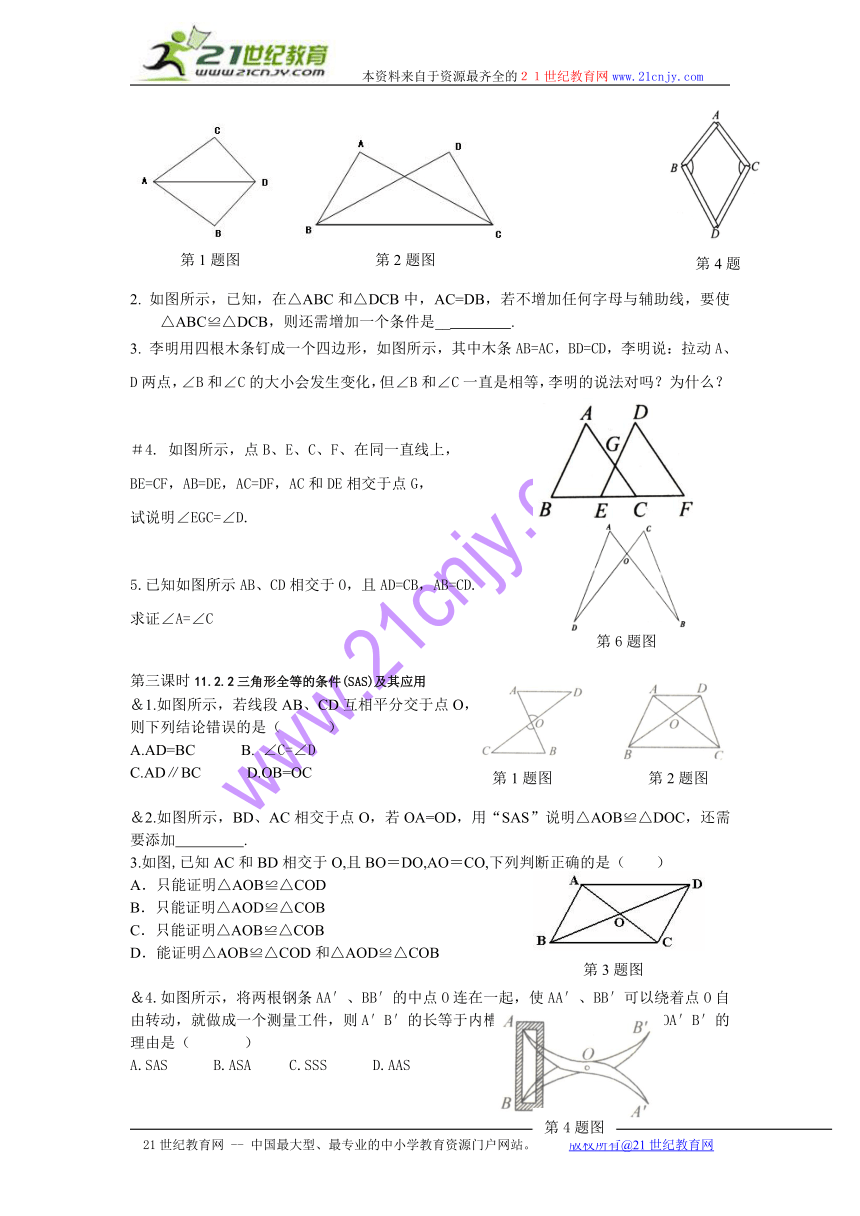
※1.如图所示,若AB=AC,DB=DC,根据 可得△ABD≌△ACD.
2. 如图所示,已知,在△ABC和△DCB中,AC=DB,若不增加任何字母与辅助线,要使△ABC≌△DCB,则还需增加一个条件是__ .
3. 李明用四根木条钉成一个四边形,如图所示,其中木条AB=AC,BD=CD,李明说:拉动A、D两点,∠B和∠C的大小会发生变化,但∠B和∠C一直是相等,李明的说法对吗?为什么?
#4. 如图所示,点B、E、C、F、在同一直线上,
BE=CF,AB=DE,AC=DF,AC和DE相交于点G,
试说明∠EGC=∠D.
5.已知如图所示AB、CD相交于O,且AD=CB,AB=CD.
求证∠A=∠C
第三课时11.2.2三角形全等的条件(SAS)及其应用
&1.如图所示,若线段AB、CD互相平分交于点O,
则下列结论错误的是( )
A.AD=BC B. ∠C=∠D
C.AD∥BC D.OB=OC
&2.如图所示,BD、AC相交于点O,若OA=OD,用“SAS”说明△AOB≌△DOC,还需要添加 .
3.如图,已知AC和BD相交于O,且BO=DO,AO=CO,下列判断正确的是( )
A.只能证明△AOB≌△COD
B.只能证明△AOD≌△COB
C.只能证明△AOB≌△COB
D.能证明△AOB≌△COD和△AOD≌△COB
&4.如图所示,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成一个测量工件,则A′B′的长等于内槽AB,那么判定△OAB≌△OA′B′的理由是( )
A.SAS B.ASA C.SSS D.AAS
※5.如图所示,已知AD∥BC,AD=BC,
试说明AB∥CD
#6. 如图,在同一直线上,在与中,,,.
(1)求证:;
(2)你还可以得到的结论是 (写出一个即可,不再添加其它线段,不再标注或使用其它字母).
#7. 如图,,,,
求证:
※8.已知AB⊥CD与B,ED⊥BC与D,AB=CD、BC=DE,
求证:AC⊥CE
第一课时答案:
1.D;2.△ECD,AB=EC,BC=CD,AC=ED, ∠A=∠E, ∠B=∠ECD, ∠ACB=∠D,3. AE=AC、BC=DE ∠B=∠ADE、∠BAC=∠DAE ;4.B,提示:MQ与NP是对应边,全等三角形的对应边相等;5.B,提示:②③正确,①④没有对应边相等;6.D;7. 95°,提示:全等三角形的对应角相等即∠C=∠D=20°,再根据三角形的内角和定理得∠OAD=95°;8.A,提示:首先要分析、观察两图中的对应部分是什么,然后再根据图形计算阴影部分的面积(全等图形的面积一定相等);9.证明:∵△ABC≌△EBD,∴∠A=∠E,又∵∠AOF=∠EOB,∴∠A+∠AOF=∠E+∠EOB,
又∵∠1=180°-(∠A+∠AOF),∠2=180°-(∠E+∠EOB),∴∠1=∠2.
第二课时答案:
1. SSS,提示:AD是公共边;2.AB=DC,提示:BC=CB是公共边;3.李明说法对.连接AD,则△ABD≌△ACD,所以∠B和∠C的大小发生变化,但∠B和∠C一直是相等的;
4. ∵BE=CF,CE=CE,∴BC=EF,在△ABC和△DEF中
∴△ABC≌△DEF,(SSS)∴∠ACB=∠F,∴AC∥DF,∴∠EGC=∠D
5.证明:连接DB,在△ADB和△CBD中∴△ADB≌△CBD(SSS)∴∠A=∠C.
第三课时答案:
1.D,提示:易证明△AOD≌△BOC而得AD=BC,∠C=∠D,由∠C=∠D得AD∥BC;
2.OB=OC;3.D;4.A,提示:本题暗含对顶角相等,故用“SAS”;5.∵AD∥BC,∴∠DAC=∠BCA
在△ADC和△CBA中∴△ADC≌△CBA. ∴∠BAC=∠DCA,∴AB∥CD.
6.(1)证明:,,
在和中
(2)答案不惟一,如:,,等.
7. 证明:,,即:
又在和△ADE中,
8.∵AB⊥CD,ED⊥BC,∴∠ABC=∠CDE=90°,在△ABC和△CDE中∴△ABC≌△CDE.∴∠A=∠ECD,∴∠ECD+∠ACB=90°,∴∠ACE=90°,∴AC⊥CE.
第1题图
第2题图
第3题图
第8题图①
第8题图②
第7题图
A
B
E
C
F
D
第6题图
第9题图
第4题图
第1题图
第2题图
第5题图
第6题图
第1题图
第2题图
第3题图
第4题图
第5题图
A
B
D
E
F
C
第6题图
1
2
第7题图
第8题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学:11.1全等三角形-11.2三角形全等的条件课时练(人教新课标八年级上)
第一课时11.1全等三角形
※1.如图所示,△ABC≌△CDA,并且BC=AD,
那么下列结论错误的是( )
A.∠1=∠2 B.AB=CD
C. ∠B=∠D D.AC=DC
&2.如图所示,△ABC沿直线BC向右平移线段
BC的长后与△ECD重合,则△ABC≌△______,
相等的边有 , ,
;相等的角有 , ,
;
3. 已知△ABC≌△ADE,∠C=∠E,AB=AD,
则另外两组对应边为________,
另外两组对应角为________.
#4.若△MNP≌△NMQ,且MN=8,NP=7,PM=6,则MQ的长为( )
A. 8 B. 7 C. 6 D.5
5.下列说法中正确的个数为( )
①所有的等边三角形都全等;②两个全等三角形的最大边是对应边;③两个全等三角形的对应角相等;④对应角相等的三角形是全等三角形.
A.1 B.2 C.3 D.4
&6. 如图,沿直角边所在的直线向右平移得到,下列结论中错误的是( )
A. B. C. D.
※7. 如图,若△OAD≌△OBC,且∠0=65°,∠C=20°,则∠OAD= .
&8. 用边长为1的正方形纸板,制成一幅七巧板(如图①),将它拼成“小天鹅”图案
(如图②),其中阴影部分的面积是( )
A. B. C. D.
#9.如图所示,已知△ABC≌△EBD
求证:∠1=∠2
第二课时11.2.1三角形全等的条件(SSS)及其应用
※1.如图所示,若AB=AC,DB=DC,根据 可得△ABD≌△ACD.
2. 如图所示,已知,在△ABC和△DCB中,AC=DB,若不增加任何字母与辅助线,要使△ABC≌△DCB,则还需增加一个条件是__ .
3. 李明用四根木条钉成一个四边形,如图所示,其中木条AB=AC,BD=CD,李明说:拉动A、D两点,∠B和∠C的大小会发生变化,但∠B和∠C一直是相等,李明的说法对吗?为什么?
#4. 如图所示,点B、E、C、F、在同一直线上,
BE=CF,AB=DE,AC=DF,AC和DE相交于点G,
试说明∠EGC=∠D.
5.已知如图所示AB、CD相交于O,且AD=CB,AB=CD.
求证∠A=∠C
第三课时11.2.2三角形全等的条件(SAS)及其应用
&1.如图所示,若线段AB、CD互相平分交于点O,
则下列结论错误的是( )
A.AD=BC B. ∠C=∠D
C.AD∥BC D.OB=OC
&2.如图所示,BD、AC相交于点O,若OA=OD,用“SAS”说明△AOB≌△DOC,还需要添加 .
3.如图,已知AC和BD相交于O,且BO=DO,AO=CO,下列判断正确的是( )
A.只能证明△AOB≌△COD
B.只能证明△AOD≌△COB
C.只能证明△AOB≌△COB
D.能证明△AOB≌△COD和△AOD≌△COB
&4.如图所示,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成一个测量工件,则A′B′的长等于内槽AB,那么判定△OAB≌△OA′B′的理由是( )
A.SAS B.ASA C.SSS D.AAS
※5.如图所示,已知AD∥BC,AD=BC,
试说明AB∥CD
#6. 如图,在同一直线上,在与中,,,.
(1)求证:;
(2)你还可以得到的结论是 (写出一个即可,不再添加其它线段,不再标注或使用其它字母).
#7. 如图,,,,
求证:
※8.已知AB⊥CD与B,ED⊥BC与D,AB=CD、BC=DE,
求证:AC⊥CE
第一课时答案:
1.D;2.△ECD,AB=EC,BC=CD,AC=ED, ∠A=∠E, ∠B=∠ECD, ∠ACB=∠D,3. AE=AC、BC=DE ∠B=∠ADE、∠BAC=∠DAE ;4.B,提示:MQ与NP是对应边,全等三角形的对应边相等;5.B,提示:②③正确,①④没有对应边相等;6.D;7. 95°,提示:全等三角形的对应角相等即∠C=∠D=20°,再根据三角形的内角和定理得∠OAD=95°;8.A,提示:首先要分析、观察两图中的对应部分是什么,然后再根据图形计算阴影部分的面积(全等图形的面积一定相等);9.证明:∵△ABC≌△EBD,∴∠A=∠E,又∵∠AOF=∠EOB,∴∠A+∠AOF=∠E+∠EOB,
又∵∠1=180°-(∠A+∠AOF),∠2=180°-(∠E+∠EOB),∴∠1=∠2.
第二课时答案:
1. SSS,提示:AD是公共边;2.AB=DC,提示:BC=CB是公共边;3.李明说法对.连接AD,则△ABD≌△ACD,所以∠B和∠C的大小发生变化,但∠B和∠C一直是相等的;
4. ∵BE=CF,CE=CE,∴BC=EF,在△ABC和△DEF中
∴△ABC≌△DEF,(SSS)∴∠ACB=∠F,∴AC∥DF,∴∠EGC=∠D
5.证明:连接DB,在△ADB和△CBD中∴△ADB≌△CBD(SSS)∴∠A=∠C.
第三课时答案:
1.D,提示:易证明△AOD≌△BOC而得AD=BC,∠C=∠D,由∠C=∠D得AD∥BC;
2.OB=OC;3.D;4.A,提示:本题暗含对顶角相等,故用“SAS”;5.∵AD∥BC,∴∠DAC=∠BCA
在△ADC和△CBA中∴△ADC≌△CBA. ∴∠BAC=∠DCA,∴AB∥CD.
6.(1)证明:,,
在和中
(2)答案不惟一,如:,,等.
7. 证明:,,即:
又在和△ADE中,
8.∵AB⊥CD,ED⊥BC,∴∠ABC=∠CDE=90°,在△ABC和△CDE中∴△ABC≌△CDE.∴∠A=∠ECD,∴∠ECD+∠ACB=90°,∴∠ACE=90°,∴AC⊥CE.
第1题图
第2题图
第3题图
第8题图①
第8题图②
第7题图
A
B
E
C
F
D
第6题图
第9题图
第4题图
第1题图
第2题图
第5题图
第6题图
第1题图
第2题图
第3题图
第4题图
第5题图
A
B
D
E
F
C
第6题图
1
2
第7题图
第8题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
