北师大版八年级数学下册1.3 线段的垂直平分线第1课时线段垂直平分线的性质与判定 教学设计 (表格式)
文档属性
| 名称 | 北师大版八年级数学下册1.3 线段的垂直平分线第1课时线段垂直平分线的性质与判定 教学设计 (表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 117.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 14:56:24 | ||
图片预览



文档简介
北师大版八年级数学下册 第一章《三角形的证明》
(同步教学设计)
3 线段的垂直平分线
第1课时 线段垂直平分线的性质与判定
课题 第2课时 线段垂直平分线的性质与判定 授课类型 新授课
授课人
教学内容 课本P22-24
教学目标 1.知识与技能 (1)要求学生掌握线段垂直平分线的性质定理及判定定理,能够利用这两个定理解决一些问题; (2)能够证明线段垂直平分线的性质定理及判定定理. 2.过程与方法 (1)经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力; (2)体验解决问题策略的多样性,发展实践能力和创新精神; (3)学会与人合作,并能与他人交流思维的过程和结果. 3.情感态度及价值观 (1)积极参与数学学习活动,对数学有好奇心和求知欲; (2)在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重难点 重点:能够证明线段的垂直平分线的性质定理、判定定理及其相关结论. 难点:(1)写出线段垂直平分线的性质定理的逆命题并证明它. (2)用尺规作线段垂直平分线.
教学准备 教师准备:课件、多媒体;学生准备:三角尺
教与学互动设计(教学过程) 设计意图
创设情景,导入新课 展示生活中的数学问题: 中卫金沙岛风景优美,其中薰衣草园、玫瑰园让不少游客流连忘返,为了方便游客旅行,计划在湖边修一个观光车车站,使它到薰衣草园和玫瑰园的距离相等,观光车车站应建在什么位置 1.所建观光车车站满足什么条件? 2.满足这个条件的点在什么地方?为什么? 3.你是怎么知道这个结论的? 师生活动:学生回忆讨论,得出结论:观光车车站应建在线段AB的垂直平分线与在A,B一侧的河岸边的交点上. 教师追问:“你能用公理或学过的定理证明这一结论吗 ” (板书课题:第1课时 线段垂直平分线的性质与判定) 通过问题情景,引导学生回顾七年级学习的线段的垂直平分线,从而引入本节课的主题——线段的垂直平分线.
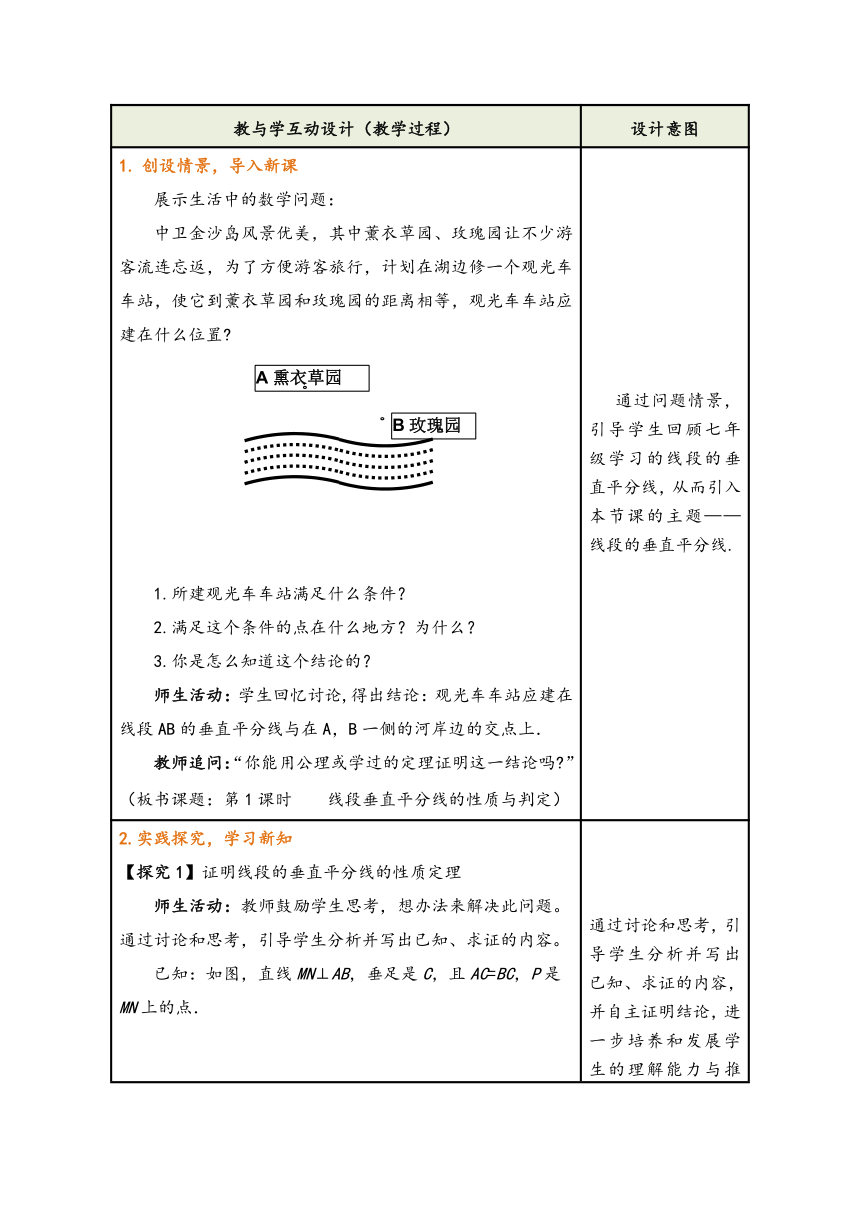
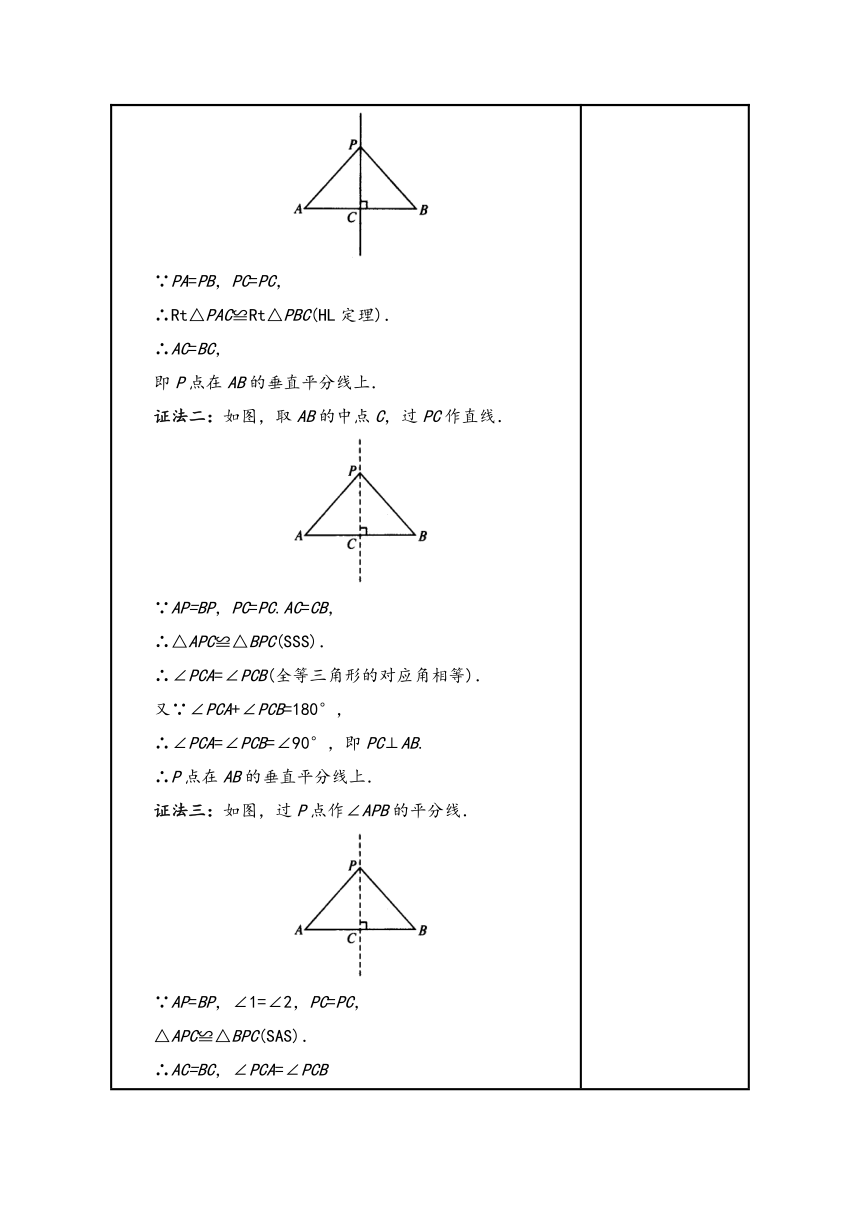
2.实践探究,学习新知 【探究1】证明线段的垂直平分线的性质定理 师生活动:教师鼓励学生思考,想办法来解决此问题。通过讨论和思考,引导学生分析并写出已知、求证的内容。 已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的点. 求证:PA=PB. 教师点拨:要想证明PA=PB,可以考虑包含这两条线段的两个三角形是否全等. 证明:∵MN⊥AB, ∴∠PCA=∠PCB=90° ∵AC=BC,PC=PC, ∴△PCA≌△PCB(SAS). ∴PA=PB(全等三角形的对应边相等). 【归纳总结】 线段的垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等. 【探究2】线段的垂直平分线的判定定理 教师提问: ①你能分析原命题的条件和结论,将原命题写成“如果……,那么……”的形式吗? ②你能写出上面这个定理的逆命题吗 最后再把它的逆命题写出来. ③它是真命题吗 如果是,请你加以证明. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明.教师注意引导学生分析证明线段的垂直平分线的判定定理. 归纳总结有如下三种证法: 证法一: 已知:线段AB,点P是平面内一点且PA=PB. 求证:P点在AB的垂直平分线上. 证明:如图,过点P作已知线段AB的垂线PC, ∵PA=PB,PC=PC, ∴Rt△PAC≌Rt△PBC(HL定理). ∴AC=BC, 即P点在AB的垂直平分线上. 证法二:如图,取AB的中点C,过PC作直线. ∵AP=BP,PC=PC.AC=CB, ∴△APC≌△BPC(SSS). ∴∠PCA=∠PCB(全等三角形的对应角相等). 又∵∠PCA+∠PCB=180°, ∴∠PCA=∠PCB=∠90°,即PC⊥AB. ∴P点在AB的垂直平分线上. 证法三:如图,过P点作∠APB的平分线. ∵AP=BP,∠1=∠2,PC=PC, △APC≌△BPC(SAS). ∴AC=BC,∠PCA=∠PCB (全等三角形的对应角相等,对应边相等). 又∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90° ∴P点在线段AB的垂直平分线上. 【归纳总结】 定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 【教材例题】 已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC. 求证:直线AO垂直平分线段BC. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明.教师注意适时引导. 证明:∵AB=AC, ∴点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上). 同理,点O在线段BC的垂直平分线上. ∴直线AO是线段BC的垂直平分线(两点确定一条直线). 通过讨论和思考,引导学生分析并写出已知、求证的内容,并自主证明结论,进一步培养和发展学生的理解能力与推理证明能力. 引导学生对性质定理进行逆向思考,提出猜想,然后加以证明.告诉学生这是获得新的结论的常用方法. 通过例题讲解,巩固强化“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上”这一定理在实际问题中的应用,培养学生的应用意识。一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
3.学以致用,应用新知 考点1 线段垂直平分线的性质定理 例 如图,在△ABC中,直线DE是线段AC的垂直平分线,若AE=3,△ABD的周长为13,则△ABC的周长为( ) A.26 B.16 C.19 D.22 答案:C 变式训练 如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E. (1)若AB=10,则△CDE的周长是多少?为什么? (2)若∠ACB=125°,求∠DCE的度数. 解:(1)△CDE的周长为10. ∵直线l与m分别是△ABC边AC和BC的垂直平分线, ∴AD=CD,BE=CE, ∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10; (2)∵直线l与m分别是△ABC边AC和BC的垂直平分线, ∴AD=CD,BE=CE, ∴∠A=∠ACD,∠B=∠BCE, 又∵∠ACB=125°, ∴∠A+∠B=180°﹣125°=55°, ∴∠ACD+∠BCE=55°, ∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°. 考点2 线段垂直平分线的判定定理 例 下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( ) A. CA=CB,DA=DB B. CA=CB,CD⊥AB C. CA=DA,CB=DB D. CA=CB,CD过AB中点 答案:C 变式训练 在△ABC中,AD垂直平分BC,点E在BC的延长线上,且满足AB+BD= DE,求证:点C在线段AE垂直平分线上. 证明:∵AD垂直平分BC, ∴BD=DC,AB=AC. 又∵AB+BD=DE, ∴AC+DC= DE. 又∵DE= DC+CE, ∴AC=CE. ∴点C在线段AE的垂直平分线上. 通过例题讲解,巩固理解线段垂直平分线的性质及判定定理,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用垂直平分线的性质定理、判定定理解决问题。
4.随堂训练,巩固新知 1.如图,AB的垂直平分线MN交AC于点D,AC=10,BC=6,则△BCD的周长为( ) A.6 B.10 C.16 D.18 答案:C 2.如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的四边形叫做筝形.AC,BD是筝形的对角线.下列结论正确的是 (填序号). ①∠DAB=∠DCB; ②∠ABC=∠ADC; ③BD 平分∠ABC; ④BD 垂真平分 AC. 答案:①③④ 3.如图,在中,,的垂直平分线分别交于点D,M.求证:点M在的垂直平分线上. 证明:连接CM, ∵DM是AC的垂直平分线, ∴AM=CM, ∴∠A=∠MCA, ∵∠ACB=90°, ∴∠A+∠B=90°,∠MCA+∠MCB=90°, ∴∠MCB=∠B, ∴CM=BM, ∴点M在BC的垂直平分线上. 4.如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,且BE=AC. (1)求证:AD⊥BC; (2)若∠C=70°,求∠BAC的度数. 解:(1)证明:如图,连接AE, ∵EF是AB的垂直平分线, ∴BE=AE, ∵BE=AC, ∴AE=AC, ∵D为线段CE的中点, ∴AD⊥BC; (2)∵AE=BE, ∴∠B=∠BAE, ∵∠AEC是△ABE的外角, ∴∠AEC=∠B+∠BAE=2∠B, ∵AE=AC, ∴∠AEC=∠C=2∠B, ∵∠C=70°, ∴∠B=35°, ∵∠B+∠C+∠BAC=180°, ∴∠BAC=180°﹣35°﹣70°=75°. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 通过本节课的学习,你学到了哪些知识? 线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等. 线段垂直平分线的判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P23习题1.7中的T1—T4. 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 线段垂直平分线的性质与判定线段垂直平分线的性质线段垂直平分线的判定投影区学生活动区
提纲掣领,重点突出。
教后反思 在这一节中,我们作为老师要善于引导学生从问题出发,根据观察、实验的结果,先得出猜想,然后再进行证明,要求学生掌握证明的基本要求和方法,注意数学压想方法的强化和渗透. 反思,更进一步提升。
(同步教学设计)
3 线段的垂直平分线
第1课时 线段垂直平分线的性质与判定
课题 第2课时 线段垂直平分线的性质与判定 授课类型 新授课
授课人
教学内容 课本P22-24
教学目标 1.知识与技能 (1)要求学生掌握线段垂直平分线的性质定理及判定定理,能够利用这两个定理解决一些问题; (2)能够证明线段垂直平分线的性质定理及判定定理. 2.过程与方法 (1)经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力; (2)体验解决问题策略的多样性,发展实践能力和创新精神; (3)学会与人合作,并能与他人交流思维的过程和结果. 3.情感态度及价值观 (1)积极参与数学学习活动,对数学有好奇心和求知欲; (2)在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重难点 重点:能够证明线段的垂直平分线的性质定理、判定定理及其相关结论. 难点:(1)写出线段垂直平分线的性质定理的逆命题并证明它. (2)用尺规作线段垂直平分线.
教学准备 教师准备:课件、多媒体;学生准备:三角尺
教与学互动设计(教学过程) 设计意图
创设情景,导入新课 展示生活中的数学问题: 中卫金沙岛风景优美,其中薰衣草园、玫瑰园让不少游客流连忘返,为了方便游客旅行,计划在湖边修一个观光车车站,使它到薰衣草园和玫瑰园的距离相等,观光车车站应建在什么位置 1.所建观光车车站满足什么条件? 2.满足这个条件的点在什么地方?为什么? 3.你是怎么知道这个结论的? 师生活动:学生回忆讨论,得出结论:观光车车站应建在线段AB的垂直平分线与在A,B一侧的河岸边的交点上. 教师追问:“你能用公理或学过的定理证明这一结论吗 ” (板书课题:第1课时 线段垂直平分线的性质与判定) 通过问题情景,引导学生回顾七年级学习的线段的垂直平分线,从而引入本节课的主题——线段的垂直平分线.
2.实践探究,学习新知 【探究1】证明线段的垂直平分线的性质定理 师生活动:教师鼓励学生思考,想办法来解决此问题。通过讨论和思考,引导学生分析并写出已知、求证的内容。 已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的点. 求证:PA=PB. 教师点拨:要想证明PA=PB,可以考虑包含这两条线段的两个三角形是否全等. 证明:∵MN⊥AB, ∴∠PCA=∠PCB=90° ∵AC=BC,PC=PC, ∴△PCA≌△PCB(SAS). ∴PA=PB(全等三角形的对应边相等). 【归纳总结】 线段的垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等. 【探究2】线段的垂直平分线的判定定理 教师提问: ①你能分析原命题的条件和结论,将原命题写成“如果……,那么……”的形式吗? ②你能写出上面这个定理的逆命题吗 最后再把它的逆命题写出来. ③它是真命题吗 如果是,请你加以证明. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明.教师注意引导学生分析证明线段的垂直平分线的判定定理. 归纳总结有如下三种证法: 证法一: 已知:线段AB,点P是平面内一点且PA=PB. 求证:P点在AB的垂直平分线上. 证明:如图,过点P作已知线段AB的垂线PC, ∵PA=PB,PC=PC, ∴Rt△PAC≌Rt△PBC(HL定理). ∴AC=BC, 即P点在AB的垂直平分线上. 证法二:如图,取AB的中点C,过PC作直线. ∵AP=BP,PC=PC.AC=CB, ∴△APC≌△BPC(SSS). ∴∠PCA=∠PCB(全等三角形的对应角相等). 又∵∠PCA+∠PCB=180°, ∴∠PCA=∠PCB=∠90°,即PC⊥AB. ∴P点在AB的垂直平分线上. 证法三:如图,过P点作∠APB的平分线. ∵AP=BP,∠1=∠2,PC=PC, △APC≌△BPC(SAS). ∴AC=BC,∠PCA=∠PCB (全等三角形的对应角相等,对应边相等). 又∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90° ∴P点在线段AB的垂直平分线上. 【归纳总结】 定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 【教材例题】 已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC. 求证:直线AO垂直平分线段BC. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明.教师注意适时引导. 证明:∵AB=AC, ∴点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上). 同理,点O在线段BC的垂直平分线上. ∴直线AO是线段BC的垂直平分线(两点确定一条直线). 通过讨论和思考,引导学生分析并写出已知、求证的内容,并自主证明结论,进一步培养和发展学生的理解能力与推理证明能力. 引导学生对性质定理进行逆向思考,提出猜想,然后加以证明.告诉学生这是获得新的结论的常用方法. 通过例题讲解,巩固强化“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上”这一定理在实际问题中的应用,培养学生的应用意识。一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。
3.学以致用,应用新知 考点1 线段垂直平分线的性质定理 例 如图,在△ABC中,直线DE是线段AC的垂直平分线,若AE=3,△ABD的周长为13,则△ABC的周长为( ) A.26 B.16 C.19 D.22 答案:C 变式训练 如图,直线l与m分别是△ABC边AC和BC的垂直平分线,l与m分别交边AB于点D和点E. (1)若AB=10,则△CDE的周长是多少?为什么? (2)若∠ACB=125°,求∠DCE的度数. 解:(1)△CDE的周长为10. ∵直线l与m分别是△ABC边AC和BC的垂直平分线, ∴AD=CD,BE=CE, ∴△CDE的周长=CD+DE+CE=AD+DE+BE=AB=10; (2)∵直线l与m分别是△ABC边AC和BC的垂直平分线, ∴AD=CD,BE=CE, ∴∠A=∠ACD,∠B=∠BCE, 又∵∠ACB=125°, ∴∠A+∠B=180°﹣125°=55°, ∴∠ACD+∠BCE=55°, ∴∠DCE=∠ACB﹣(∠ACD+∠BCE)=125°﹣55°=70°. 考点2 线段垂直平分线的判定定理 例 下列条件中,不能判定直线CD是线段AB(C,D不在线段AB上)的垂直平分线的是( ) A. CA=CB,DA=DB B. CA=CB,CD⊥AB C. CA=DA,CB=DB D. CA=CB,CD过AB中点 答案:C 变式训练 在△ABC中,AD垂直平分BC,点E在BC的延长线上,且满足AB+BD= DE,求证:点C在线段AE垂直平分线上. 证明:∵AD垂直平分BC, ∴BD=DC,AB=AC. 又∵AB+BD=DE, ∴AC+DC= DE. 又∵DE= DC+CE, ∴AC=CE. ∴点C在线段AE的垂直平分线上. 通过例题讲解,巩固理解线段垂直平分线的性质及判定定理,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用垂直平分线的性质定理、判定定理解决问题。
4.随堂训练,巩固新知 1.如图,AB的垂直平分线MN交AC于点D,AC=10,BC=6,则△BCD的周长为( ) A.6 B.10 C.16 D.18 答案:C 2.如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的四边形叫做筝形.AC,BD是筝形的对角线.下列结论正确的是 (填序号). ①∠DAB=∠DCB; ②∠ABC=∠ADC; ③BD 平分∠ABC; ④BD 垂真平分 AC. 答案:①③④ 3.如图,在中,,的垂直平分线分别交于点D,M.求证:点M在的垂直平分线上. 证明:连接CM, ∵DM是AC的垂直平分线, ∴AM=CM, ∴∠A=∠MCA, ∵∠ACB=90°, ∴∠A+∠B=90°,∠MCA+∠MCB=90°, ∴∠MCB=∠B, ∴CM=BM, ∴点M在BC的垂直平分线上. 4.如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,且BE=AC. (1)求证:AD⊥BC; (2)若∠C=70°,求∠BAC的度数. 解:(1)证明:如图,连接AE, ∵EF是AB的垂直平分线, ∴BE=AE, ∵BE=AC, ∴AE=AC, ∵D为线段CE的中点, ∴AD⊥BC; (2)∵AE=BE, ∴∠B=∠BAE, ∵∠AEC是△ABE的外角, ∴∠AEC=∠B+∠BAE=2∠B, ∵AE=AC, ∴∠AEC=∠C=2∠B, ∵∠C=70°, ∴∠B=35°, ∵∠B+∠C+∠BAC=180°, ∴∠BAC=180°﹣35°﹣70°=75°. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 通过本节课的学习,你学到了哪些知识? 线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等. 线段垂直平分线的判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P23习题1.7中的T1—T4. 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 线段垂直平分线的性质与判定线段垂直平分线的性质线段垂直平分线的判定投影区学生活动区
提纲掣领,重点突出。
教后反思 在这一节中,我们作为老师要善于引导学生从问题出发,根据观察、实验的结果,先得出猜想,然后再进行证明,要求学生掌握证明的基本要求和方法,注意数学压想方法的强化和渗透. 反思,更进一步提升。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
