北师大版八年级数学下册 1.3线段的垂直平分线(第2课时)线段垂直平分线的综合应用教学设计(表格式)
文档属性
| 名称 | 北师大版八年级数学下册 1.3线段的垂直平分线(第2课时)线段垂直平分线的综合应用教学设计(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 166.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 15:06:26 | ||
图片预览



文档简介
北师大版八年级数学下册 第一章《三角形的证明》
(同步教学设计)
3 线段的垂直平分线
第2课时 线段垂直平分线的综合应用
课题 第2课时 线段垂直平分线的综合应用 授课类型 新授课
授课人
教学内容 课本P24-27
教学目标 1.能够证明三角形三边垂直平分线交于一点 2.经历猜想、探索,能够作出符合条件的三角形. 3.经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力.体验解决问题的方法,发展实践能力和创新意识. 4.学会与他人合作,并能与他人交流思维的过程和结果.
教学重难点 重点: ①能够证明与线段垂直平分线相关的结论. ②已知底边和底边上的高,能利用尺规作出等腰三角形. 难点:证明三线共点。
教学准备 教师准备:课件、多媒体;学生准备:三角尺、三角形纸片(三种)、圆规和直尺
教与学互动设计(教学过程) 设计意图
创设情景,导入新课 展示生活中的数学问题: 某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等? 师生活动:猜想:要到三个小区的距离相等,那么应建在三角形三边垂直平分线的交点. 教师追问:那三角形三边的垂直平分线是否交于一点呢? (板书课题:第1课时 线段垂直平分线的综合应用) 通过问题情景,引导学生思考线段垂直平分线的性质,使学生感受到学习三角形三边的垂直平分线的性质是实际需要,进而引出对三角形三边的垂直平分线性质的探讨.
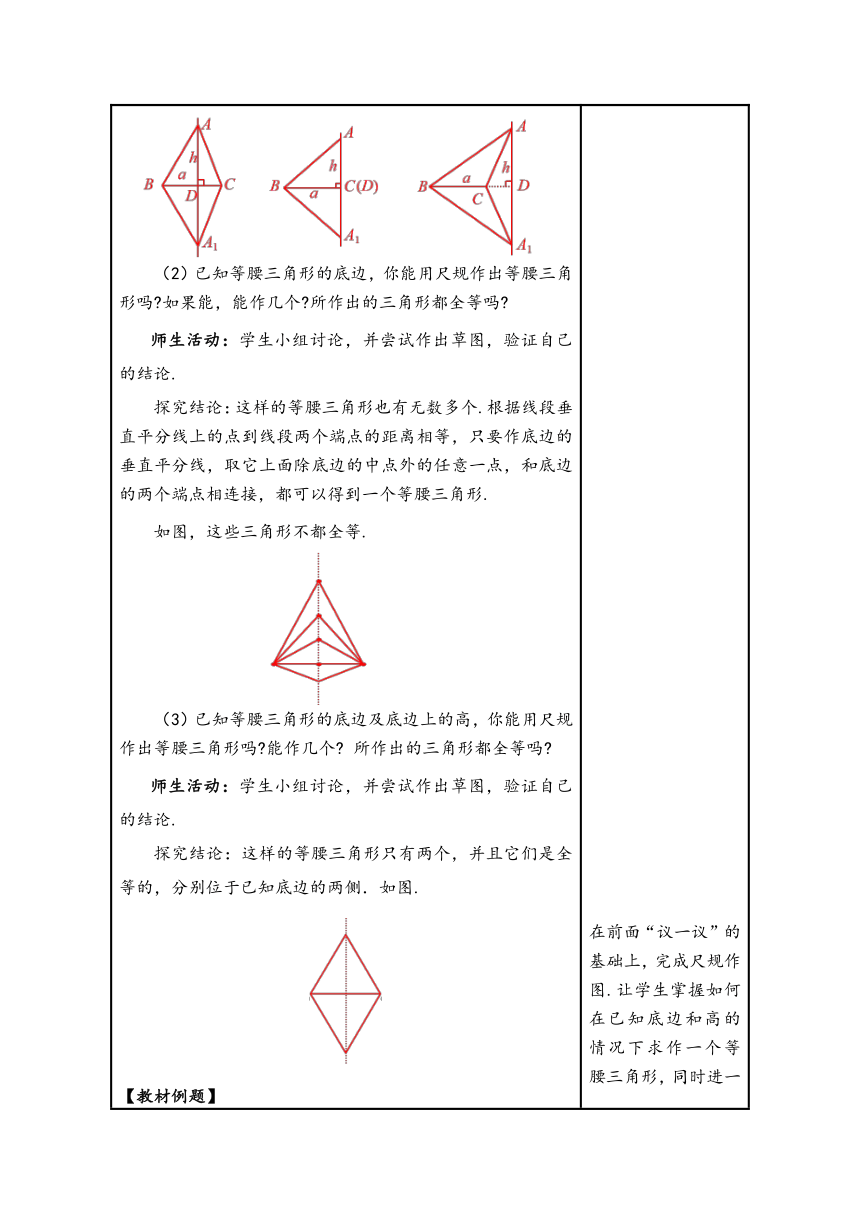
2.实践探究,学习新知 【探究1】探索三角形三边的垂直平分线的性质 师生活动: 1.利用尺规作三角形三条边的垂直平分线:用尺规作图法分别作出三角形、直角三角形、钝角三角形的三边垂直平分线,总结交点的位置,并且测量交点到三个顶点的距离。 2.剪下一个三角形,通过折叠找出每边的垂直平分线,并总结锐角、直角、钝角三种三角形三边垂直平分线交点的情况。 你有什么样的发现?与同组同学之间相互交流. 学生活动:在学生小组合作的基础上,经过讨论分析,学生自主归纳总结. 【归纳总结】 三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等. 【探究2】证明三角形三边的垂直平分线的性质 求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等. 已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P. 求证:边AC的垂直平分线经过点P,且PA=PB=PC. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明.教师注意适时引导. 证明:∵点P在线段AB的垂直平分线上, ∴PA=PB(线段垂直平分线上 的点到这条线段两个端点的距离相等) 同理,PB=PC. ∴PA=PB=PC. ∴点P在线段AC的垂直平分线上(到一条线段两个端点距离相等的点, 在这条线段的垂直平分线上), 即边AC的垂直平分线经过点P. 【归纳总结】 三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等. 【探究3】已知等腰三角形的底边和该边上的高,求作等腰三角形 议一议: (1)已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗 师生活动:学生小组讨论,并尝试作出草图,验证自己的结论. 探究结论:能作出无数个这样的三角形,它们并不全等.如图. (2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗 如果能,能作几个 所作出的三角形都全等吗 师生活动:学生小组讨论,并尝试作出草图,验证自己的结论. 探究结论:这样的等腰三角形也有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形. 如图,这些三角形不都全等. (3)已知等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗 能作几个 所作出的三角形都全等吗 师生活动:学生小组讨论,并尝试作出草图,验证自己的结论. 探究结论:这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.如图. 【教材例题】 已知一个等腰三角形的底及底边上的高,求作这个等腰三角形. 已知:如图①,线段a,h. 求作:△ABC,使AB=AC,且BC=a,高AD=h. 师生活动:教师应引导学生体会每一作图步骤的作用及其理论依据. 作法: (1)作线段BC=a(如图). (2)作线段BC的垂直平分线l, 交BC于点D. (3)在l上作线段DA,使DA=h. (4)连接AB,AC. △ABC为所求的等腰三角形. 通过动手操作让学生探索三角形三边垂直平分线的性质,提高学习兴趣,加深学生的直观印象. 引导学生分析三角形三边垂直平分线的性质命题,画出图形,写出已知和求证。 这里设置的三个问题为学生进行尺规作图的探索提供了思考空间,同时也为例3的学习奠定了基础. 在前面“议一议”的基础上,完成尺规作图.让学生掌握如何在已知底边和高的情况下求作一个等腰三角形,同时进一步使学生掌握线段垂直平分线的作法.
3.学以致用,应用新知 考点1 三角形三边垂直平分线的性质 例 某地兴建的幸福家园的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该安装在△ABC( ) A.三条边的垂直平分线的交点 B.三个角的角平分线的交点 C.三角形三条高的交点 D.三角形三条中线的交点 答案:A 变式训练 如图,点P为△ABC三边垂直平分线的交点,若∠PAC=20°,∠PCB=30°,则∠PAB的度数为 . 答案:40° 考点2 与垂直平分线相关的尺规作图 例 如图,在△ABC中,∠C=90°,分别以A、B为圆心画弧,所画的弧交于两点,再连接该两点所在直线交BC于点D,连接AD.若BD=2,则AD的长为( ) A. B. C.1 D.2 答案:D 变式训练 如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为( ) A.5 B.4 C.3 D.2 答案:A 通过例题讲解,巩固理解线段垂直平分线的综合应用,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用线段垂直平分线的知识解决问题。
4.随堂训练,巩固新知 1.在△ABC的BC边上找一点P,使得PA+PC=BC.下面找法正确的是( ) A.以B为圆心,BA为半径画弧,交BC于点P,点P为所求 B.以C为圆心,CA为半径画弧,交BC于点P,点P为所求 C.作AC的垂直平分线交BC于点P,点P为所求 D.作AB的垂直平分线交BC于点P,点P为所求 答案:D 2.如图,点D是△ABC三边垂直平分线的交点,若∠D=116°,则∠A=( ) A.64° B.58° C.52° D.68° 答案:B 3.如图,在△ABC中,∠B=68°,∠C=28°,分别以点A和点C为圆心,大于0.5AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( ) A.50° B.52° C.54° D.56° 4.如图,线段AB,BC的垂直平分线l1,l2相交于点O,连接OA,OC,AC,若∠ABC=40°,则∠AOC=___________. 答案:80° 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 通过本节课的学习,你学到了哪些知识? 线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等. 线段垂直平分线的判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P26习题1.8中的T1—T4. 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第2课时 线段垂直平分线的综合应用三角形三边的线段垂直平分线的性质与线段垂直平分线有关的作图投影区学生活动区
提纲掣领,重点突出。
教后反思 本节课证明了线段垂直平分线的性质定理和判定定理,并能利用尺规作出已知线段的垂直平分线.已知等腰三角形的底边和高作出符合条件的等腰三角形,从尺规作图,逻辑推理多层次地理解并证明了三角形三边的垂直平分线交于一点,并且这一点到三角形三个顶点的距离相等。 反思,更进一步提升。
(同步教学设计)
3 线段的垂直平分线
第2课时 线段垂直平分线的综合应用
课题 第2课时 线段垂直平分线的综合应用 授课类型 新授课
授课人
教学内容 课本P24-27
教学目标 1.能够证明三角形三边垂直平分线交于一点 2.经历猜想、探索,能够作出符合条件的三角形. 3.经历探索、猜测、证明的过程,进一步发展学生的推理证明意识和能力.体验解决问题的方法,发展实践能力和创新意识. 4.学会与他人合作,并能与他人交流思维的过程和结果.
教学重难点 重点: ①能够证明与线段垂直平分线相关的结论. ②已知底边和底边上的高,能利用尺规作出等腰三角形. 难点:证明三线共点。
教学准备 教师准备:课件、多媒体;学生准备:三角尺、三角形纸片(三种)、圆规和直尺
教与学互动设计(教学过程) 设计意图
创设情景,导入新课 展示生活中的数学问题: 某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等? 师生活动:猜想:要到三个小区的距离相等,那么应建在三角形三边垂直平分线的交点. 教师追问:那三角形三边的垂直平分线是否交于一点呢? (板书课题:第1课时 线段垂直平分线的综合应用) 通过问题情景,引导学生思考线段垂直平分线的性质,使学生感受到学习三角形三边的垂直平分线的性质是实际需要,进而引出对三角形三边的垂直平分线性质的探讨.
2.实践探究,学习新知 【探究1】探索三角形三边的垂直平分线的性质 师生活动: 1.利用尺规作三角形三条边的垂直平分线:用尺规作图法分别作出三角形、直角三角形、钝角三角形的三边垂直平分线,总结交点的位置,并且测量交点到三个顶点的距离。 2.剪下一个三角形,通过折叠找出每边的垂直平分线,并总结锐角、直角、钝角三种三角形三边垂直平分线交点的情况。 你有什么样的发现?与同组同学之间相互交流. 学生活动:在学生小组合作的基础上,经过讨论分析,学生自主归纳总结. 【归纳总结】 三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等. 【探究2】证明三角形三边的垂直平分线的性质 求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等. 已知:如图,在△ABC中,边AB的垂直平分线与边BC的垂直平分线相交于点P. 求证:边AC的垂直平分线经过点P,且PA=PB=PC. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明.教师注意适时引导. 证明:∵点P在线段AB的垂直平分线上, ∴PA=PB(线段垂直平分线上 的点到这条线段两个端点的距离相等) 同理,PB=PC. ∴PA=PB=PC. ∴点P在线段AC的垂直平分线上(到一条线段两个端点距离相等的点, 在这条线段的垂直平分线上), 即边AC的垂直平分线经过点P. 【归纳总结】 三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等. 【探究3】已知等腰三角形的底边和该边上的高,求作等腰三角形 议一议: (1)已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗 师生活动:学生小组讨论,并尝试作出草图,验证自己的结论. 探究结论:能作出无数个这样的三角形,它们并不全等.如图. (2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗 如果能,能作几个 所作出的三角形都全等吗 师生活动:学生小组讨论,并尝试作出草图,验证自己的结论. 探究结论:这样的等腰三角形也有无数多个.根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形. 如图,这些三角形不都全等. (3)已知等腰三角形的底边及底边上的高,你能用尺规作出等腰三角形吗 能作几个 所作出的三角形都全等吗 师生活动:学生小组讨论,并尝试作出草图,验证自己的结论. 探究结论:这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.如图. 【教材例题】 已知一个等腰三角形的底及底边上的高,求作这个等腰三角形. 已知:如图①,线段a,h. 求作:△ABC,使AB=AC,且BC=a,高AD=h. 师生活动:教师应引导学生体会每一作图步骤的作用及其理论依据. 作法: (1)作线段BC=a(如图). (2)作线段BC的垂直平分线l, 交BC于点D. (3)在l上作线段DA,使DA=h. (4)连接AB,AC. △ABC为所求的等腰三角形. 通过动手操作让学生探索三角形三边垂直平分线的性质,提高学习兴趣,加深学生的直观印象. 引导学生分析三角形三边垂直平分线的性质命题,画出图形,写出已知和求证。 这里设置的三个问题为学生进行尺规作图的探索提供了思考空间,同时也为例3的学习奠定了基础. 在前面“议一议”的基础上,完成尺规作图.让学生掌握如何在已知底边和高的情况下求作一个等腰三角形,同时进一步使学生掌握线段垂直平分线的作法.
3.学以致用,应用新知 考点1 三角形三边垂直平分线的性质 例 某地兴建的幸福家园的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该安装在△ABC( ) A.三条边的垂直平分线的交点 B.三个角的角平分线的交点 C.三角形三条高的交点 D.三角形三条中线的交点 答案:A 变式训练 如图,点P为△ABC三边垂直平分线的交点,若∠PAC=20°,∠PCB=30°,则∠PAB的度数为 . 答案:40° 考点2 与垂直平分线相关的尺规作图 例 如图,在△ABC中,∠C=90°,分别以A、B为圆心画弧,所画的弧交于两点,再连接该两点所在直线交BC于点D,连接AD.若BD=2,则AD的长为( ) A. B. C.1 D.2 答案:D 变式训练 如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知△CDE的面积比△CDB的面积小5,则△ADE的面积为( ) A.5 B.4 C.3 D.2 答案:A 通过例题讲解,巩固理解线段垂直平分线的综合应用,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用线段垂直平分线的知识解决问题。
4.随堂训练,巩固新知 1.在△ABC的BC边上找一点P,使得PA+PC=BC.下面找法正确的是( ) A.以B为圆心,BA为半径画弧,交BC于点P,点P为所求 B.以C为圆心,CA为半径画弧,交BC于点P,点P为所求 C.作AC的垂直平分线交BC于点P,点P为所求 D.作AB的垂直平分线交BC于点P,点P为所求 答案:D 2.如图,点D是△ABC三边垂直平分线的交点,若∠D=116°,则∠A=( ) A.64° B.58° C.52° D.68° 答案:B 3.如图,在△ABC中,∠B=68°,∠C=28°,分别以点A和点C为圆心,大于0.5AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( ) A.50° B.52° C.54° D.56° 4.如图,线段AB,BC的垂直平分线l1,l2相交于点O,连接OA,OC,AC,若∠ABC=40°,则∠AOC=___________. 答案:80° 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 通过本节课的学习,你学到了哪些知识? 线段垂直平分线的性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等. 线段垂直平分线的判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P26习题1.8中的T1—T4. 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第2课时 线段垂直平分线的综合应用三角形三边的线段垂直平分线的性质与线段垂直平分线有关的作图投影区学生活动区
提纲掣领,重点突出。
教后反思 本节课证明了线段垂直平分线的性质定理和判定定理,并能利用尺规作出已知线段的垂直平分线.已知等腰三角形的底边和高作出符合条件的等腰三角形,从尺规作图,逻辑推理多层次地理解并证明了三角形三边的垂直平分线交于一点,并且这一点到三角形三个顶点的距离相等。 反思,更进一步提升。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
