北师大版八年级数学下册1.1第3课时 等腰三角形的判定与反证法 同步教学设计(表格式)
文档属性
| 名称 | 北师大版八年级数学下册1.1第3课时 等腰三角形的判定与反证法 同步教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 119.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 16:30:55 | ||
图片预览


文档简介
北师大版八年级数学下册 第一章《三角形的证明》
(同步教学设计)
1 等腰三角形
第3课时 等腰三角形的判定与反证法
课题 第3课时 等腰三角形的判定与反证法 授课类型 新授课
授课人
教学内容 课本P8-10
教学目标 1.探索等腰三角形判定定理. 2.理解等腰三角形的判定定理,并会运用其进行简单的证明. 3.了解反证法的基本证明思路,并能简单应用。 4.培养学生的逆向思维能力。
教学重难点 重点:等腰三角形的判定定理的证明,结合实例体会反证法的含义. 难点:运用“等边对等角”解决实际应用问题及相关证明.
教学准备 课件、三角尺、等腰三角形纸片
教与学互动设计(教学过程) 设计意图
创设情景,导入新课 【情景1】 展示生活中的数学问题: 某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(A点)为目标,然后在这棵树的正南方南岸B点插一小旗作标志,沿南偏东60度方向走一段距离到C处时,测得∠ACB为30度,这时,地质专家测得BC的长度是50米,就可知河流宽度是50米. 师生活动: 同学们,你们想知道这样估测河流宽度的根据是什么吗?地质学家是怎么知道BC的长度是等于河流宽度的呢?今天我们就要学习等腰三角形的判定. 【情景2】 欣赏故事“道旁苦李”: 《世说新语》记载:王戎七岁,尝与诸小儿游.道边李树多子折枝,诸儿竞去取之,唯戎不动.人问之,答曰:“树在道边而多子,必苦李.”取之,信然. 师生活动:说说这个故事和数学知识间的联系. (板书课题:第3课时 等腰三角形的判定与反证法) 通过生活实际问题引入等腰三角形的判定,来激发学生学习数学的兴趣,使学生感受到学习等腰三角形的判定是实际需要,进而顺利引入新课。 通过生活中的“道旁苦李”的小故事引入反证法,激发学生学习数学的兴趣,使学生很自然地进入本节的学习,进而顺利引入新课。
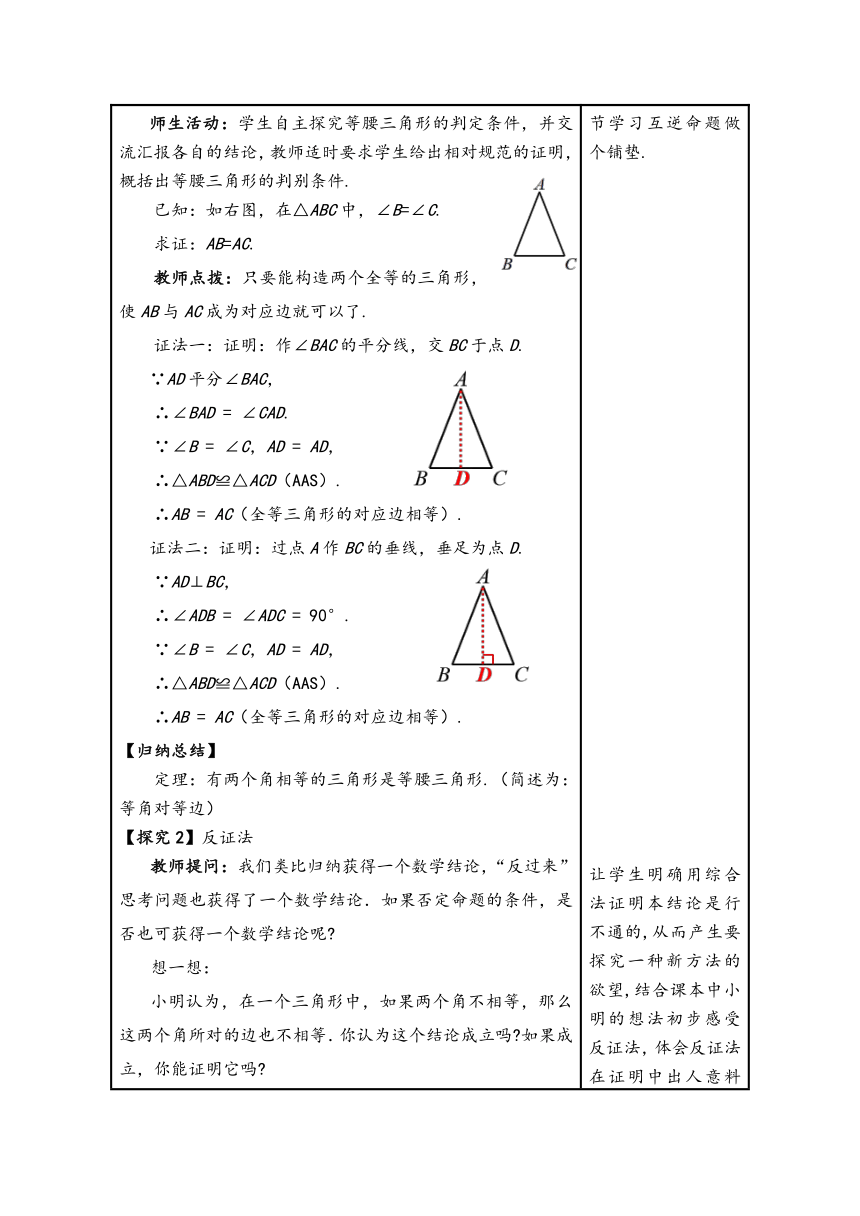
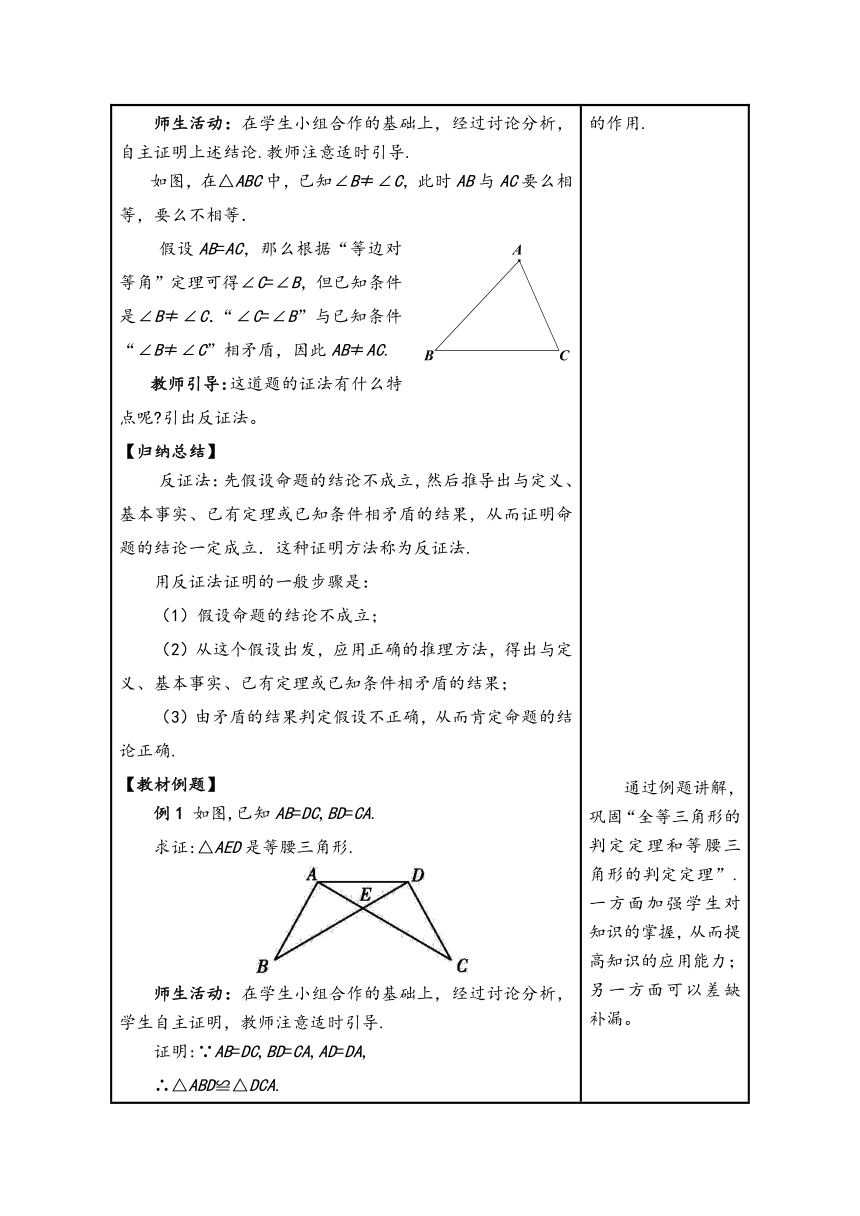
2.实践探究,学习新知 【探究1】等腰三角形的判定 教师提问: 问题1:等腰三角形性质定理的内容是什么?这个命题的题设和结论分别是什么? 问题2:我们是如何证明上述定理的? 问题3:前面已经证明了等腰三角形的两个底角相等,反过来,有两个角相等的三角形是等腰三角形吗?你有几种证明方法? 师生活动:学生自主探究等腰三角形的判定条件,并交流汇报各自的结论,教师适时要求学生给出相对规范的证明,概括出等腰三角形的判别条件. 已知:如右图,在△ABC中,∠B=∠C. 求证:AB=AC. 教师点拨:只要能构造两个全等的三角形,使AB与AC成为对应边就可以了. 证法一:证明:作∠BAC的平分线,交BC于点D. ∵AD平分∠BAC, ∴∠BAD = ∠CAD. ∵∠B = ∠C,AD = AD, ∴△ABD≌△ACD(AAS). ∴AB = AC(全等三角形的对应边相等). 证法二:证明:过点A作BC的垂线,垂足为点D. ∵AD⊥BC, ∴∠ADB = ∠ADC = 90°. ∵∠B = ∠C,AD = AD, ∴△ABD≌△ACD(AAS). ∴AB = AC(全等三角形的对应边相等). 【归纳总结】 定理:有两个角相等的三角形是等腰三角形.(简述为:等角对等边) 【探究2】反证法 教师提问:我们类比归纳获得一个数学结论,“反过来”思考问题也获得了一个数学结论.如果否定命题的条件,是否也可获得一个数学结论呢 想一想: 小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗 如果成立,你能证明它吗 师生活动:在学生小组合作的基础上,经过讨论分析,自主证明上述结论.教师注意适时引导. 如图,在△ABC中,已知∠B≠∠C,此时AB与AC要么相等,要么不相等. 假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,但已知条件是∠B≠∠C.“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,因此AB≠AC. 教师引导:这道题的证法有什么特点呢 引出反证法。 【归纳总结】 反证法:先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法. 用反证法证明的一般步骤是: (1)假设命题的结论不成立; (2)从这个假设出发,应用正确的推理方法,得出与定义、基本事实、已有定理或已知条件相矛盾的结果; (3)由矛盾的结果判定假设不正确,从而肯定命题的结论正确. 【教材例题】 例1 如图,已知AB=DC,BD=CA. 求证:△AED是等腰三角形. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明,教师注意适时引导. 证明:∵AB=DC,BD=CA,AD=DA, ∴△ABD≌△DCA. ∴∠ADB=∠DAC(全等三角形对应角相等), ∴AE=DE(等角对等边), ∴△AED是等腰三角形. 在解答过程中,教师应关注学生的思考过程,引导学生分析解决问题的方法. 例2 反证法证明:一个三角形中不能有两个角是直角. 已知:△ABC, 求证:∠A,∠B,∠C中不能有两个角是直角. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明一个三角形中不能有两个角是直角.教师注意适时引导. 证明:假设∠A,∠B,∠C中有两个角是直角, 不妨设∠A和∠B是直角, 即∠A=90°,∠B=90°, 于是∠A+∠B+∠C=90°+90°+∠C>180°, 这与三角形内角和定理相矛盾, 因此“∠A和∠B都是直角”的假设不成立. 所以,一个三角形中不能有两个角是直角. 引导学生养成“反过来”思考问题的意识,即思考一个命题的逆命题的真假,因为这也是获得数学结论的一条重要途径.同时,这样设置问题也为学生下一节学习互逆命题做个铺垫. 让学生明确用综合法证明本结论是行不通的,从而产生要探究一种新方法的欲望,结合课本中小明的想法初步感受反证法,体会反证法在证明中出人意料的作用. 通过例题讲解,巩固“全等三角形的判定定理和等腰三角形的判定定理”.一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 以例题形式展示用反证法证明命题的过程.让学生感受反证法的证明思路与书写的过程,体会反证法的证明与作用.
3.学以致用,应用新知 考点1 等腰三角形的判定定理 例 如图,在△ABC中,AC=BC,∠C=36°,AD平分∠BAC,则图中等腰三角形的个数是( ) A. 1个 B. 2个 C. 3个 D. 4个 答案:C 变式训练 如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B处.分别从A、B处望灯塔C,测得∠NAC=42°,∠NBC=84°.求B处与灯塔C距离. 解:∵∠NBC是△ABC的外角 ∴∠C=∠NBC﹣∠NAC=42° ∴∠C=∠BAC ∴BC=BA=18×10=180(海里) 因此B处与灯塔C距离是180海里. 考点2 反证法 例 如已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤: ①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾 ②因此假设不成立.∴∠B<90° ③假设在△ABC中,∠B≥90° ④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°. 这四个步骤正确的顺序应是( ) A.④③①② B.③④②① C.①②③④ D.③④①② 答案:D 变式训练 用反证法证明:等腰三角形的底角是锐角. 证明:假设等腰三角形的底角不是锐角,则大于或等于90°. 根据等腰三角形的两个底角相等,则两个底角的和大于或等于180°. 则该三角形的三个内角的和一定大于180°,这与三角形的内角和定理相矛盾,故假设不成立. 所以等腰三角形的底角是锐角. 通过例题讲解,巩固理解等腰三角形的判定定理(等角对等边),一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用等腰三角形的判定定理解决问题。 通过例题讲解,巩固理解反证法,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用反证法进行证明。
4.随堂训练,巩固新知 1.选择用反证法证明“已知:在△ABC中,∠C=90°,求证:∠A,∠B中至少有一个角不大于45°”时,应先假设( ) A.∠A≤45°,∠B≤45° B.∠A≥45°,∠B≥45° C.∠A<45°,∠B<45° D.∠A>45°,∠B>45° 答案:D 2. 已知五个正数的和为1,用反证法证明:这五个正数中至少有一个大于或等于. 证明:假设这五个正数a1,a2,a3,a4,a5中没有一个大于或等于,即都小于,那么a1+a2+a3+a4+a5<5×=1,这与已知a1+a2+a3+a4+a5=1矛盾.所以原命题得证. 3 已知:如图,在△ABC中,AD∥BC,AD平分外角EAC,求证:AB=AC. 证明:∵AD∥BC, ∴∠B=∠EAD,∠C=∠DAC, ∵AD平分外角EAC, ∴∠EAD=∠DAC, ∴∠B=∠C. ∴AB=AC. 4.已知:如图△ABC中AB=6 cm,AC=8 cm,BD平分∠ABC,CD平分∠ACB,过D作直线平行于BC,交AB,AC于E,F. (1)求证:△DFC是等腰三角形; (2)求△AEF的周长. 解:(1)证明:∵EF∥BC, ∴∠FDC=∠DCB, ∵CD平分∠ACB, ∴∠FCD=∠BCD, ∴∠FCD=∠FDC, ∴FD=FC, ∴△DFC是等腰三角形; (2)∵EF∥BC, ∴∠EDB=∠DBC, ∵BD平分∠ABC, ∴∠DBC=∠DBE, ∴∠EDB=∠DBE, ∴DE=BE, ∵DF=FC, ∴△AEF的周长=AE+AF+DE+DF=AE+AF+BE+FC=AB+AC, ∵AB=8 cm,AC=6 cm, ∴AB+AC=8+6=14(cm), ∴△AEF的周长为14 cm. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 通过本节课的学习,你学到了哪些知识? 证明两个三角形全等的方法: 两边及其夹角分别相等(SAS)、两角及其夹边分别相等(ASA)、三边分别相等(SSS)、两角和其中一角的对边分别相等(AAS). 根据全等三角形的定义,我们可以得到: 全等三角形的对应边相等、对应角相等. 等腰三角形的性质: 1.等腰三角形的两底角相等.(等边对等角) 2.等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.(三线合一) 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P4习题1.2中的T1—T4. 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 三角形全等与等腰三角形的性质一、全等三角形的判定二、等腰三角形的性质投影区1性质2.推论学生活动区
提纲掣领,重点突出。
教后反思 本节课让学生在认识等腰三角形的基础上,进一步认识等边三角形.学习等边三角形的定义、性质和判定.让学生在探索图形特征以及相关结论的活动中,进一步发展空间观念,锻炼思维能力.让学生在学习活动中,进一步产生对数学的好奇心,增强动手能力和创新意识.在这节课中,要学生充分的自主探究,尝试提出问题和解决问题,发展学生的自主探究能力. 反思,更进一步提升。
(同步教学设计)
1 等腰三角形
第3课时 等腰三角形的判定与反证法
课题 第3课时 等腰三角形的判定与反证法 授课类型 新授课
授课人
教学内容 课本P8-10
教学目标 1.探索等腰三角形判定定理. 2.理解等腰三角形的判定定理,并会运用其进行简单的证明. 3.了解反证法的基本证明思路,并能简单应用。 4.培养学生的逆向思维能力。
教学重难点 重点:等腰三角形的判定定理的证明,结合实例体会反证法的含义. 难点:运用“等边对等角”解决实际应用问题及相关证明.
教学准备 课件、三角尺、等腰三角形纸片
教与学互动设计(教学过程) 设计意图
创设情景,导入新课 【情景1】 展示生活中的数学问题: 某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(A点)为目标,然后在这棵树的正南方南岸B点插一小旗作标志,沿南偏东60度方向走一段距离到C处时,测得∠ACB为30度,这时,地质专家测得BC的长度是50米,就可知河流宽度是50米. 师生活动: 同学们,你们想知道这样估测河流宽度的根据是什么吗?地质学家是怎么知道BC的长度是等于河流宽度的呢?今天我们就要学习等腰三角形的判定. 【情景2】 欣赏故事“道旁苦李”: 《世说新语》记载:王戎七岁,尝与诸小儿游.道边李树多子折枝,诸儿竞去取之,唯戎不动.人问之,答曰:“树在道边而多子,必苦李.”取之,信然. 师生活动:说说这个故事和数学知识间的联系. (板书课题:第3课时 等腰三角形的判定与反证法) 通过生活实际问题引入等腰三角形的判定,来激发学生学习数学的兴趣,使学生感受到学习等腰三角形的判定是实际需要,进而顺利引入新课。 通过生活中的“道旁苦李”的小故事引入反证法,激发学生学习数学的兴趣,使学生很自然地进入本节的学习,进而顺利引入新课。
2.实践探究,学习新知 【探究1】等腰三角形的判定 教师提问: 问题1:等腰三角形性质定理的内容是什么?这个命题的题设和结论分别是什么? 问题2:我们是如何证明上述定理的? 问题3:前面已经证明了等腰三角形的两个底角相等,反过来,有两个角相等的三角形是等腰三角形吗?你有几种证明方法? 师生活动:学生自主探究等腰三角形的判定条件,并交流汇报各自的结论,教师适时要求学生给出相对规范的证明,概括出等腰三角形的判别条件. 已知:如右图,在△ABC中,∠B=∠C. 求证:AB=AC. 教师点拨:只要能构造两个全等的三角形,使AB与AC成为对应边就可以了. 证法一:证明:作∠BAC的平分线,交BC于点D. ∵AD平分∠BAC, ∴∠BAD = ∠CAD. ∵∠B = ∠C,AD = AD, ∴△ABD≌△ACD(AAS). ∴AB = AC(全等三角形的对应边相等). 证法二:证明:过点A作BC的垂线,垂足为点D. ∵AD⊥BC, ∴∠ADB = ∠ADC = 90°. ∵∠B = ∠C,AD = AD, ∴△ABD≌△ACD(AAS). ∴AB = AC(全等三角形的对应边相等). 【归纳总结】 定理:有两个角相等的三角形是等腰三角形.(简述为:等角对等边) 【探究2】反证法 教师提问:我们类比归纳获得一个数学结论,“反过来”思考问题也获得了一个数学结论.如果否定命题的条件,是否也可获得一个数学结论呢 想一想: 小明认为,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗 如果成立,你能证明它吗 师生活动:在学生小组合作的基础上,经过讨论分析,自主证明上述结论.教师注意适时引导. 如图,在△ABC中,已知∠B≠∠C,此时AB与AC要么相等,要么不相等. 假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,但已知条件是∠B≠∠C.“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,因此AB≠AC. 教师引导:这道题的证法有什么特点呢 引出反证法。 【归纳总结】 反证法:先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法. 用反证法证明的一般步骤是: (1)假设命题的结论不成立; (2)从这个假设出发,应用正确的推理方法,得出与定义、基本事实、已有定理或已知条件相矛盾的结果; (3)由矛盾的结果判定假设不正确,从而肯定命题的结论正确. 【教材例题】 例1 如图,已知AB=DC,BD=CA. 求证:△AED是等腰三角形. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明,教师注意适时引导. 证明:∵AB=DC,BD=CA,AD=DA, ∴△ABD≌△DCA. ∴∠ADB=∠DAC(全等三角形对应角相等), ∴AE=DE(等角对等边), ∴△AED是等腰三角形. 在解答过程中,教师应关注学生的思考过程,引导学生分析解决问题的方法. 例2 反证法证明:一个三角形中不能有两个角是直角. 已知:△ABC, 求证:∠A,∠B,∠C中不能有两个角是直角. 师生活动:在学生小组合作的基础上,经过讨论分析,学生自主证明一个三角形中不能有两个角是直角.教师注意适时引导. 证明:假设∠A,∠B,∠C中有两个角是直角, 不妨设∠A和∠B是直角, 即∠A=90°,∠B=90°, 于是∠A+∠B+∠C=90°+90°+∠C>180°, 这与三角形内角和定理相矛盾, 因此“∠A和∠B都是直角”的假设不成立. 所以,一个三角形中不能有两个角是直角. 引导学生养成“反过来”思考问题的意识,即思考一个命题的逆命题的真假,因为这也是获得数学结论的一条重要途径.同时,这样设置问题也为学生下一节学习互逆命题做个铺垫. 让学生明确用综合法证明本结论是行不通的,从而产生要探究一种新方法的欲望,结合课本中小明的想法初步感受反证法,体会反证法在证明中出人意料的作用. 通过例题讲解,巩固“全等三角形的判定定理和等腰三角形的判定定理”.一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 以例题形式展示用反证法证明命题的过程.让学生感受反证法的证明思路与书写的过程,体会反证法的证明与作用.
3.学以致用,应用新知 考点1 等腰三角形的判定定理 例 如图,在△ABC中,AC=BC,∠C=36°,AD平分∠BAC,则图中等腰三角形的个数是( ) A. 1个 B. 2个 C. 3个 D. 4个 答案:C 变式训练 如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B处.分别从A、B处望灯塔C,测得∠NAC=42°,∠NBC=84°.求B处与灯塔C距离. 解:∵∠NBC是△ABC的外角 ∴∠C=∠NBC﹣∠NAC=42° ∴∠C=∠BAC ∴BC=BA=18×10=180(海里) 因此B处与灯塔C距离是180海里. 考点2 反证法 例 如已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤: ①∴∠A+∠B+∠C>180°,这与三角形内角和为180°矛盾 ②因此假设不成立.∴∠B<90° ③假设在△ABC中,∠B≥90° ④由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°. 这四个步骤正确的顺序应是( ) A.④③①② B.③④②① C.①②③④ D.③④①② 答案:D 变式训练 用反证法证明:等腰三角形的底角是锐角. 证明:假设等腰三角形的底角不是锐角,则大于或等于90°. 根据等腰三角形的两个底角相等,则两个底角的和大于或等于180°. 则该三角形的三个内角的和一定大于180°,这与三角形的内角和定理相矛盾,故假设不成立. 所以等腰三角形的底角是锐角. 通过例题讲解,巩固理解等腰三角形的判定定理(等角对等边),一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用等腰三角形的判定定理解决问题。 通过例题讲解,巩固理解反证法,一方面加强学生对知识的掌握,从而提高知识的应用能力;另一方面可以差缺补漏。 通过变式训练巩固所学知识,灵活运用反证法进行证明。
4.随堂训练,巩固新知 1.选择用反证法证明“已知:在△ABC中,∠C=90°,求证:∠A,∠B中至少有一个角不大于45°”时,应先假设( ) A.∠A≤45°,∠B≤45° B.∠A≥45°,∠B≥45° C.∠A<45°,∠B<45° D.∠A>45°,∠B>45° 答案:D 2. 已知五个正数的和为1,用反证法证明:这五个正数中至少有一个大于或等于. 证明:假设这五个正数a1,a2,a3,a4,a5中没有一个大于或等于,即都小于,那么a1+a2+a3+a4+a5<5×=1,这与已知a1+a2+a3+a4+a5=1矛盾.所以原命题得证. 3 已知:如图,在△ABC中,AD∥BC,AD平分外角EAC,求证:AB=AC. 证明:∵AD∥BC, ∴∠B=∠EAD,∠C=∠DAC, ∵AD平分外角EAC, ∴∠EAD=∠DAC, ∴∠B=∠C. ∴AB=AC. 4.已知:如图△ABC中AB=6 cm,AC=8 cm,BD平分∠ABC,CD平分∠ACB,过D作直线平行于BC,交AB,AC于E,F. (1)求证:△DFC是等腰三角形; (2)求△AEF的周长. 解:(1)证明:∵EF∥BC, ∴∠FDC=∠DCB, ∵CD平分∠ACB, ∴∠FCD=∠BCD, ∴∠FCD=∠FDC, ∴FD=FC, ∴△DFC是等腰三角形; (2)∵EF∥BC, ∴∠EDB=∠DBC, ∵BD平分∠ABC, ∴∠DBC=∠DBE, ∴∠EDB=∠DBE, ∴DE=BE, ∵DF=FC, ∴△AEF的周长=AE+AF+DE+DF=AE+AF+BE+FC=AB+AC, ∵AB=8 cm,AC=6 cm, ∴AB+AC=8+6=14(cm), ∴△AEF的周长为14 cm. 为学生提供自我检测的机会,教师针对学生的学习情况,及时调整授课,查缺补漏。
5.课堂小结,自我完善 通过本节课的学习,你学到了哪些知识? 证明两个三角形全等的方法: 两边及其夹角分别相等(SAS)、两角及其夹边分别相等(ASA)、三边分别相等(SSS)、两角和其中一角的对边分别相等(AAS). 根据全等三角形的定义,我们可以得到: 全等三角形的对应边相等、对应角相等. 等腰三角形的性质: 1.等腰三角形的两底角相等.(等边对等角) 2.等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.(三线合一) 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容。
6.布置作业 课本P4习题1.2中的T1—T4. 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率。
板书设计 第1课时 三角形全等与等腰三角形的性质一、全等三角形的判定二、等腰三角形的性质投影区1性质2.推论学生活动区
提纲掣领,重点突出。
教后反思 本节课让学生在认识等腰三角形的基础上,进一步认识等边三角形.学习等边三角形的定义、性质和判定.让学生在探索图形特征以及相关结论的活动中,进一步发展空间观念,锻炼思维能力.让学生在学习活动中,进一步产生对数学的好奇心,增强动手能力和创新意识.在这节课中,要学生充分的自主探究,尝试提出问题和解决问题,发展学生的自主探究能力. 反思,更进一步提升。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
