湘教版初中数学八年级上册1.4分式的加法和减法 课件(共32张PPT)
文档属性
| 名称 | 湘教版初中数学八年级上册1.4分式的加法和减法 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
1.4 分式的加法和减法
第1章 分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
同分母的分式的加减法
分式的通分
异分母的分式的加减法
分式的混合运算
知识点
同分母的分式的加减法
知1-讲
感悟新知
1
1. 同分母的分式的加、减法运算法则:
同分母的分式相加减,分母不变,把分子相加减.
即
知1-讲
感悟新知
2. 同分母的分式相加减的一般步骤:
(1)分母不变,把分子相加减;
(2)分子相加减时,应先去括
号,再合并同类项;
(3)结果应化成最简分式或整式.
特别解读
“分子相加减”就是把各个分式的分子整体相加减,在计算时,各分子都应用括号括起来,若分子是系数为正的单项式,括号可以省略;若分子是多项式,且分子相减时,括号不能省略,否则容易出现符号错误.
感悟新知
知1-练
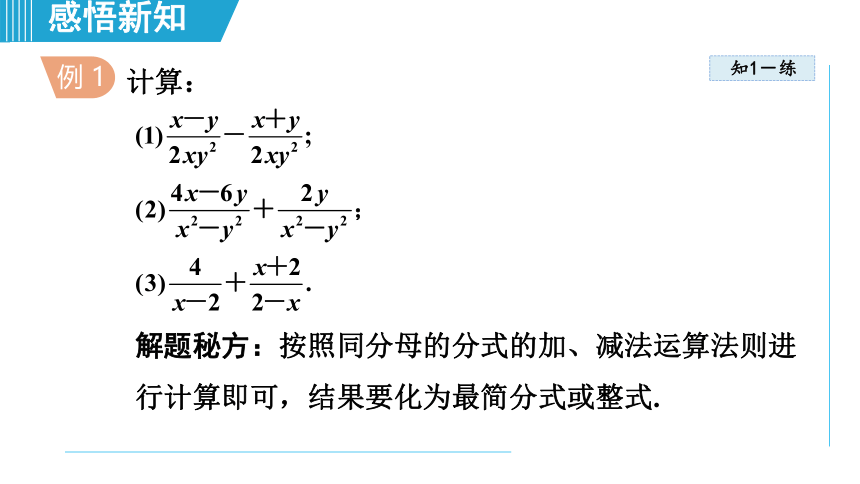
计算:
例 1
解题秘方:按照同分母的分式的加、减法运算法则进行计算即可,结果要化为最简分式或整式.
感悟新知
知1-练
警示误区
1. 当分母不相同而是相反数时,不能直接相加减,需将分母变为相同的,同时,中间的运算符号之改变,即“+”号变“-”号,“-”号变“+”号;
2. 当分子是多项式时,在对分子进行加减时,要带括号,后去括号运算;
3. 加减运算后,对运算的结果要化简,最后的结果应是最简分式或整式.
感悟新知
知1-练
知识点
分式的通分
知2-讲
感悟新知
2
1. 分式的通分:根据分式的基本性质,把几个异分母的分式化成同分母的分式的过程,叫作分式的通分.
2. 最简公分母:通分时,一般取各分母的所有因式的最高次幂的积作为公分母,这样的公分母称为最简公分母.
知2-讲
感悟新知
3. 通分的一般步骤:
(1)确定最简公分母;
(2)用最简公分母分别除以各分母求商;
(3)用所得的商分别乘相应分式的分子、分母得出同分母分式.
知2-讲
感悟新知
特别解读
约分与通分的联系与区别:
约分与通分都是对分式进行恒等变形,即变形之后每个分式的值都不变.
约分是针对一个分式来说的,约分可使分式得以化简,而通分是针对两个或两个以上的分式来说的,通分可使异分母的分式化为同分母的分式.
感悟新知
知2-练
把下列各组分式通分:
例2
知2-讲
感悟新知
教你一招
确定最简公分母的一般方法:
如果各分母都是单项式,那么最简公分母就是由①各分母系数的最小公倍数; ②各分母相同字母的最高次幂;③各分母所有不同字母及其指数的乘积这三部分组成;
如果各分母中有多项式,就先把分母是多项式的分解因式,再按照分母都是单项式时求最简公分母的方法,从系数、相同因式、不同因式三个方面去确定.
解题秘方:先确定最简公分母,再通分.
感悟新知
知2-练
感悟新知
知2-练
感悟新知
知2-练
知识点
异分母的分式的加减法
知3-讲
感悟新知
3
1. 异分母的分式的加、减法运算法则:
异分母的分式进行加、减运算时,要先化成同分母的分式,然后再加减. 即
知3-讲
感悟新知
2. 异分母的分式相加减的一般步骤:
(1)通分:将异分母的分式转化为同分母的分式;
(2)加减:按照同分母的分式进行加减运算时的一般步骤进行计算.
注意:异分母的分式进行
加减运算时的关键是通分.
特别解读
通分的关键是确定最简公分母,最简公分母是各分母的所有因式的最高次幂的积.
感悟新知
知3-练
计算:
解题秘方:异分母的分式相加减,先找最简公分母,进行通分,变为同分母的分式,再按照同分母的分式的加、减法运算法则进行计算.
例 3
感悟新知
知3-练
特别提醒
1. 通分时,若要改变某个因式的符号,可利用分式的符号变化规律进行变换.
2. 类似同分母的分式相加减,分子是多项式的注意带上括号.
3. 最后运算的结果应是最简分式或整式.
感悟新知
知3-练
在通分时,整式看成分母是1,整式作为分子的“分式”,若是多项式时,则看成一个整体;通分时要带上括号
感悟新知
知3-练
从甲地到乙地有两条路,每条路都是3 km,其中第
一条是平路,第二条有1 km 的上坡路,2 km 的下坡路,小亮在上坡路上的骑车速度为a km/h,在平路上的骑车速度为2a km/h,在下坡路上的骑车速度为3a km/h.
(1)当他分别走第一条路和第二条路时,从甲地到乙地各需要多长时间?
(2)从甲地到乙地,他走哪条路花费的时间少?少用多长时间?
例 3
感悟新知
知3-练
解题秘方:紧扣题意中揭示的数量关系,利用分式的运算结果解决问题.
思路点拨
(1) 根据时间=路程÷速度,求出走这两条路分别花费的时间;
(2)将走这两条路分别花费的时间作差,比较大小,差的绝对值就是少用的时间.
感悟新知
知3-练
解:(1)走第一条路所用的时间为 h.
走第二条路所用的时间为
知识点
分式的混合运算
知4-讲
感悟新知
4
1. 分式的混合运算顺序:
分式与分数的混合运算有相同的运算顺序,即先乘方,再乘除,然后加减. 有括号时,先做括号内的运算,按照小括号、中括号、大括号的顺序进行,对于同级运算,按从左到右的顺序进行.
知4-讲
感悟新知
2. 分式的混合运算的方法:
(1)进行分式混合运算时,可以根据需要合理运用运算律来简化运算,此时需将分式的乘除法统一成乘法,分式的加减法统一成加法,才能使用乘法运算律、加法运算律简化运算.
(2)运算过程中及时约分化简,有时可使解题过程简单.
(3)运算结果是最简分式或整式.
知4-讲
感悟新知
特别提醒
◆分式的混合运算要注意运算顺序和解题步骤,把好符号关.
◆分式除法只有转化为乘法后才能运用乘法运算律进行计算.
感悟新知
知4-练
计算:
解题秘方:在进行分式的混合运算时,应先算乘方,再算乘除,最后算加减,有括号时要先算括号里面的.
例 5
感悟新知
知4-练
方法点拨
1. 分式的计算应先分清运算顺序,再按分式的运算法则进行计算,当某一项是整式时,可将此项看成分母为1 的式子.
2. 分式的混合运算中要注意对各分式中分子、分母符号的处理,结果中分子或分母的系数是负数的,要把“-”号提到分式的前面.
3. 所有的分式运算,结果必须化到最简.
感悟新知
知4-练
感悟新知
知4-练
课堂小结
分式的加法和减法
分式的加法和减法
同分母
异分母
混合
运算
运算顺序
运算律
与乘除组成
必做: 请完成教材课后习题
补充: 请完成《典中点》对应习题
课后作业
作业1
作业2
1.4 分式的加法和减法
第1章 分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
同分母的分式的加减法
分式的通分
异分母的分式的加减法
分式的混合运算
知识点
同分母的分式的加减法
知1-讲
感悟新知
1
1. 同分母的分式的加、减法运算法则:
同分母的分式相加减,分母不变,把分子相加减.
即
知1-讲
感悟新知
2. 同分母的分式相加减的一般步骤:
(1)分母不变,把分子相加减;
(2)分子相加减时,应先去括
号,再合并同类项;
(3)结果应化成最简分式或整式.
特别解读
“分子相加减”就是把各个分式的分子整体相加减,在计算时,各分子都应用括号括起来,若分子是系数为正的单项式,括号可以省略;若分子是多项式,且分子相减时,括号不能省略,否则容易出现符号错误.
感悟新知
知1-练
计算:
例 1
解题秘方:按照同分母的分式的加、减法运算法则进行计算即可,结果要化为最简分式或整式.
感悟新知
知1-练
警示误区
1. 当分母不相同而是相反数时,不能直接相加减,需将分母变为相同的,同时,中间的运算符号之改变,即“+”号变“-”号,“-”号变“+”号;
2. 当分子是多项式时,在对分子进行加减时,要带括号,后去括号运算;
3. 加减运算后,对运算的结果要化简,最后的结果应是最简分式或整式.
感悟新知
知1-练
知识点
分式的通分
知2-讲
感悟新知
2
1. 分式的通分:根据分式的基本性质,把几个异分母的分式化成同分母的分式的过程,叫作分式的通分.
2. 最简公分母:通分时,一般取各分母的所有因式的最高次幂的积作为公分母,这样的公分母称为最简公分母.
知2-讲
感悟新知
3. 通分的一般步骤:
(1)确定最简公分母;
(2)用最简公分母分别除以各分母求商;
(3)用所得的商分别乘相应分式的分子、分母得出同分母分式.
知2-讲
感悟新知
特别解读
约分与通分的联系与区别:
约分与通分都是对分式进行恒等变形,即变形之后每个分式的值都不变.
约分是针对一个分式来说的,约分可使分式得以化简,而通分是针对两个或两个以上的分式来说的,通分可使异分母的分式化为同分母的分式.
感悟新知
知2-练
把下列各组分式通分:
例2
知2-讲
感悟新知
教你一招
确定最简公分母的一般方法:
如果各分母都是单项式,那么最简公分母就是由①各分母系数的最小公倍数; ②各分母相同字母的最高次幂;③各分母所有不同字母及其指数的乘积这三部分组成;
如果各分母中有多项式,就先把分母是多项式的分解因式,再按照分母都是单项式时求最简公分母的方法,从系数、相同因式、不同因式三个方面去确定.
解题秘方:先确定最简公分母,再通分.
感悟新知
知2-练
感悟新知
知2-练
感悟新知
知2-练
知识点
异分母的分式的加减法
知3-讲
感悟新知
3
1. 异分母的分式的加、减法运算法则:
异分母的分式进行加、减运算时,要先化成同分母的分式,然后再加减. 即
知3-讲
感悟新知
2. 异分母的分式相加减的一般步骤:
(1)通分:将异分母的分式转化为同分母的分式;
(2)加减:按照同分母的分式进行加减运算时的一般步骤进行计算.
注意:异分母的分式进行
加减运算时的关键是通分.
特别解读
通分的关键是确定最简公分母,最简公分母是各分母的所有因式的最高次幂的积.
感悟新知
知3-练
计算:
解题秘方:异分母的分式相加减,先找最简公分母,进行通分,变为同分母的分式,再按照同分母的分式的加、减法运算法则进行计算.
例 3
感悟新知
知3-练
特别提醒
1. 通分时,若要改变某个因式的符号,可利用分式的符号变化规律进行变换.
2. 类似同分母的分式相加减,分子是多项式的注意带上括号.
3. 最后运算的结果应是最简分式或整式.
感悟新知
知3-练
在通分时,整式看成分母是1,整式作为分子的“分式”,若是多项式时,则看成一个整体;通分时要带上括号
感悟新知
知3-练
从甲地到乙地有两条路,每条路都是3 km,其中第
一条是平路,第二条有1 km 的上坡路,2 km 的下坡路,小亮在上坡路上的骑车速度为a km/h,在平路上的骑车速度为2a km/h,在下坡路上的骑车速度为3a km/h.
(1)当他分别走第一条路和第二条路时,从甲地到乙地各需要多长时间?
(2)从甲地到乙地,他走哪条路花费的时间少?少用多长时间?
例 3
感悟新知
知3-练
解题秘方:紧扣题意中揭示的数量关系,利用分式的运算结果解决问题.
思路点拨
(1) 根据时间=路程÷速度,求出走这两条路分别花费的时间;
(2)将走这两条路分别花费的时间作差,比较大小,差的绝对值就是少用的时间.
感悟新知
知3-练
解:(1)走第一条路所用的时间为 h.
走第二条路所用的时间为
知识点
分式的混合运算
知4-讲
感悟新知
4
1. 分式的混合运算顺序:
分式与分数的混合运算有相同的运算顺序,即先乘方,再乘除,然后加减. 有括号时,先做括号内的运算,按照小括号、中括号、大括号的顺序进行,对于同级运算,按从左到右的顺序进行.
知4-讲
感悟新知
2. 分式的混合运算的方法:
(1)进行分式混合运算时,可以根据需要合理运用运算律来简化运算,此时需将分式的乘除法统一成乘法,分式的加减法统一成加法,才能使用乘法运算律、加法运算律简化运算.
(2)运算过程中及时约分化简,有时可使解题过程简单.
(3)运算结果是最简分式或整式.
知4-讲
感悟新知
特别提醒
◆分式的混合运算要注意运算顺序和解题步骤,把好符号关.
◆分式除法只有转化为乘法后才能运用乘法运算律进行计算.
感悟新知
知4-练
计算:
解题秘方:在进行分式的混合运算时,应先算乘方,再算乘除,最后算加减,有括号时要先算括号里面的.
例 5
感悟新知
知4-练
方法点拨
1. 分式的计算应先分清运算顺序,再按分式的运算法则进行计算,当某一项是整式时,可将此项看成分母为1 的式子.
2. 分式的混合运算中要注意对各分式中分子、分母符号的处理,结果中分子或分母的系数是负数的,要把“-”号提到分式的前面.
3. 所有的分式运算,结果必须化到最简.
感悟新知
知4-练
感悟新知
知4-练
课堂小结
分式的加法和减法
分式的加法和减法
同分母
异分母
混合
运算
运算顺序
运算律
与乘除组成
必做: 请完成教材课后习题
补充: 请完成《典中点》对应习题
课后作业
作业1
作业2
同课章节目录
