2024年高考数学考前回归教材材料3 学案
文档属性
| 名称 | 2024年高考数学考前回归教材材料3 学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 14:17:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
模块一:集合与逻辑用语
1、元素与集合
(1) 元素与集合的含义
元素:一般地,把研究对象统称为元素,常用小写拉丁字母 表示.
集合: 把一些元素组成的总体叫做集合 (简称集). 用大写拉丁字母 表示.
(2) 集合相等: 只要构成两个集合的元素是一样的, 我们就称这两个集合是相等的; 反过来, 当这两个集合相等 时, 这两个集合中的元素是完全相同的.
2、元素与集合的关系
关系 概念 记法 读法
属于 是集合 的元素,就说 属于集合 属于集合
不属于 不是集合 中的元素,就说 不属于集合 不属于集合
3、集合中元素的三个特性(判断是否是集合的依据)
(1) : 对任意一个元素, 要么它属于某个指定集合, 要么它不属于该集合, 二者必居其一;
(2) (同一个集合中的元素是互不相同的, 相同的元素只能出现一次;
(3) _____ : 集合中的元素没有先后顺序.
4、集合的分类
(1) 按元素属性分类: 数集、点集、图形集等;
(2) 按元素个数分类: 有限集、无限集
5、集合表示方法
(1) 列举法:
(2) 描述法:
描述法表示集合的基本形式:
(3) 图示法: Venn 图和数轴表示集合.
6、常用数集符号
常用数集 自然数集 正整数集 整数集 有理数集 实数集 复数集
符号表示
7、集合间的基本关系
(1) 集合间的关系:
语言概括 符号表示 Venn 图 相关性质
子集
真子集
集合相等 (1) 且 (2) 两个集合中的元素相同
(2) 空集: 把不含任何元素的集合叫做空集,记作: ; 规定: 空集是任何集合的子集: 空集是任何非空集合的 真子集.
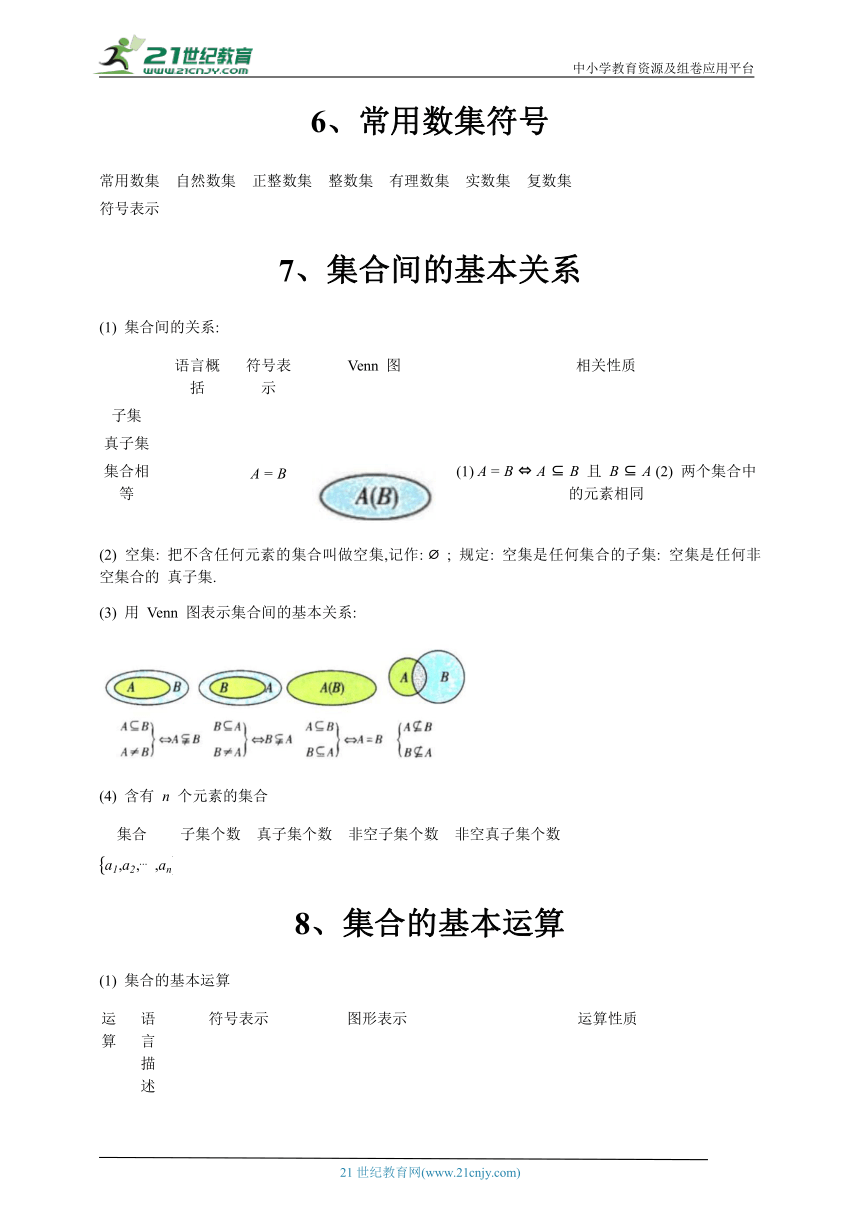
(3) 用 Venn 图表示集合间的基本关系:
(4) 含有 个元素的集合
集合 子集个数 真子集个数 非空子集个数 非空真子集个数
8、集合的基本运算
(1) 集合的基本运算
运算 语言描述 符号表示 图形表示 运算性质
并集 或 (1) ; (2) ; (3) ; (4) ; (5) ; (6) ,
交集
补集
(2) 全集: 如果一个集合含有我们所研究问题中涉及的所有元素,就称这个集合为全集,通常记作 .
(3) 德 摩根定律:
(1) (2)
(4) 集合中元素个数计算 (阅读课本人教 A 版 P15-P16)
(1) ;
(2)
9、充分条件与必要条件
(1) 充分条件与必要条件
一般地,“若 ,则 ” 为真命题,是指由 通过推理可以得出 . 即由 退出 ,记作:
并说________的充分条件,_______的必要条件. (2) 充分条件、必要条件、充要条件的判断
定义法判断 集合语言判断
是 充分不必要 条件
是 必要不充分 条件
是 充要条件
是 既不充分也 不必要条件 且
注: 把 研究的范围看成集合 ,把 研究的范围看成集合 ,记
(3) 充要条件的证明:
(1)证明 “ 是 充要条件”,要分别从 “ ” 和 “ ” 两个方面证明,即要分别证明充分性和必要 性两个方面, 但是, 在表述中要注意充分性与必要性对应的关系.
(2)要分清命题中的条件和结论,防止把充分性和必要性弄颠倒,由条件 结论是证明充分性,由结论 条 件是证明必要性.
10、全称量词与存在量词
(1) 全称量词与全称量词命题
语言定义 符号表示
全称量词 短语中在逻辑中成为全称量词
全称量词命题 含有全称量词的命题
全称量词命题 (1) 判断全称量词命题是真命题,需要对每一个元素 ,证明都成立; 的判断(2) 判断全称量词命题是假命题, 举反例.
(2) 存在量词与存在量词命题
语言定义 符号表示
存在量词 短语中在逻辑中成为存在量词
存在量词命题 含有存在量词的命题
存在量词命题 (1) 判断存在量词命题是真命题, 举例说明; 的判断(2) 判断全称量词命题是假命题,需要对每一个元素 ,证明都不成立; .
(3) 量词的否定
命题形式 否定
存在量词命题
存在量词命题
全称量词命题的否定是存在量词命题; 存在量词命题的否定是全程量词
【课本优质习题汇总】
新人教 A 版必修一 P14
6. 已知全集 ,试求集合 .
新人教 A 版必修一 P23
5. 设 . 证明: 的充要条件是 .
6. 设 分别是 的三条边,且 . 我们知道,如果 为直角三角形,那 么 (勾股定理). 反过来,如果 ,那么 为直角三角形 (勾股定理 的逆定理). 由此可知, 为直角三角形的充要条件是 .
请利用边长 分别给出 为锐角三角形和钝角三角形的一个充要条件,并证明.
新人教 A 版必修一 P35
11. 学校举办运动会时, 高一 (1) 班共有 28 名同学参加比赛, 有 15 人参加游泳比赛, 有 8 人参 加田径比赛, 有 14 人参加球类比赛, 同时参加游泳比赛和田径比赛的有 3 人, 同时参加游泳 比赛和球类比赛的有 3 人, 没有人同时参加三项比赛. 同时参加田径和球类比赛的有多少人 只参加游泳一项比赛的有多少人
12. 根据下述事实, 分别写出含有量词的全称量词命题或存在量词命题:
(第 12 (2) 题)
(1) ,
......
(2) 如图,在 中, 与 分别为 与 边上的高,则 与 所在的直线交于一点 .新人教 B 版必修一 P22
(1) 已知集合 ,且 ,求 的值.
(2) 已知集合 ,若 ,求 的取值范围.
(3) 已知 ,且 , 求 的取值范围.
(3) 已知 为全集 的非空真子集,且 与 不相等,若 , 试判断集合 和 的关系,并求出 .
新人教 B 版必修一 P31
(3) 已知区间 ,且 “ ” 是真命题,求实数 的取 值范围.
新人教 B 版必修一 P38
判断下列命题的真假:
(1) ; (2) .
(2) 判断下列命题的真假:
(1) ;
(2) .
新人教 B 版必修一 P42
1. 已知 ,求 中所含元素的个数.
2. 已知集合 , ,定义集合
求 中元素的个数.
3. 若 ,求 的值.
4. 若 ,求 的值.
5. 设 为全集, 是集合,判断 “存在集合 ,使得 ” 是 “ ” 的什么条件.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
模块一:集合与逻辑用语
1、元素与集合
(1) 元素与集合的含义
元素:一般地,把研究对象统称为元素,常用小写拉丁字母 表示.
集合: 把一些元素组成的总体叫做集合 (简称集). 用大写拉丁字母 表示.
(2) 集合相等: 只要构成两个集合的元素是一样的, 我们就称这两个集合是相等的; 反过来, 当这两个集合相等 时, 这两个集合中的元素是完全相同的.
2、元素与集合的关系
关系 概念 记法 读法
属于 是集合 的元素,就说 属于集合 属于集合
不属于 不是集合 中的元素,就说 不属于集合 不属于集合
3、集合中元素的三个特性(判断是否是集合的依据)
(1) : 对任意一个元素, 要么它属于某个指定集合, 要么它不属于该集合, 二者必居其一;
(2) (同一个集合中的元素是互不相同的, 相同的元素只能出现一次;
(3) _____ : 集合中的元素没有先后顺序.
4、集合的分类
(1) 按元素属性分类: 数集、点集、图形集等;
(2) 按元素个数分类: 有限集、无限集
5、集合表示方法
(1) 列举法:
(2) 描述法:
描述法表示集合的基本形式:
(3) 图示法: Venn 图和数轴表示集合.
6、常用数集符号
常用数集 自然数集 正整数集 整数集 有理数集 实数集 复数集
符号表示
7、集合间的基本关系
(1) 集合间的关系:
语言概括 符号表示 Venn 图 相关性质
子集
真子集
集合相等 (1) 且 (2) 两个集合中的元素相同
(2) 空集: 把不含任何元素的集合叫做空集,记作: ; 规定: 空集是任何集合的子集: 空集是任何非空集合的 真子集.
(3) 用 Venn 图表示集合间的基本关系:
(4) 含有 个元素的集合
集合 子集个数 真子集个数 非空子集个数 非空真子集个数
8、集合的基本运算
(1) 集合的基本运算
运算 语言描述 符号表示 图形表示 运算性质
并集 或 (1) ; (2) ; (3) ; (4) ; (5) ; (6) ,
交集
补集
(2) 全集: 如果一个集合含有我们所研究问题中涉及的所有元素,就称这个集合为全集,通常记作 .
(3) 德 摩根定律:
(1) (2)
(4) 集合中元素个数计算 (阅读课本人教 A 版 P15-P16)
(1) ;
(2)
9、充分条件与必要条件
(1) 充分条件与必要条件
一般地,“若 ,则 ” 为真命题,是指由 通过推理可以得出 . 即由 退出 ,记作:
并说________的充分条件,_______的必要条件. (2) 充分条件、必要条件、充要条件的判断
定义法判断 集合语言判断
是 充分不必要 条件
是 必要不充分 条件
是 充要条件
是 既不充分也 不必要条件 且
注: 把 研究的范围看成集合 ,把 研究的范围看成集合 ,记
(3) 充要条件的证明:
(1)证明 “ 是 充要条件”,要分别从 “ ” 和 “ ” 两个方面证明,即要分别证明充分性和必要 性两个方面, 但是, 在表述中要注意充分性与必要性对应的关系.
(2)要分清命题中的条件和结论,防止把充分性和必要性弄颠倒,由条件 结论是证明充分性,由结论 条 件是证明必要性.
10、全称量词与存在量词
(1) 全称量词与全称量词命题
语言定义 符号表示
全称量词 短语中在逻辑中成为全称量词
全称量词命题 含有全称量词的命题
全称量词命题 (1) 判断全称量词命题是真命题,需要对每一个元素 ,证明都成立; 的判断(2) 判断全称量词命题是假命题, 举反例.
(2) 存在量词与存在量词命题
语言定义 符号表示
存在量词 短语中在逻辑中成为存在量词
存在量词命题 含有存在量词的命题
存在量词命题 (1) 判断存在量词命题是真命题, 举例说明; 的判断(2) 判断全称量词命题是假命题,需要对每一个元素 ,证明都不成立; .
(3) 量词的否定
命题形式 否定
存在量词命题
存在量词命题
全称量词命题的否定是存在量词命题; 存在量词命题的否定是全程量词
【课本优质习题汇总】
新人教 A 版必修一 P14
6. 已知全集 ,试求集合 .
新人教 A 版必修一 P23
5. 设 . 证明: 的充要条件是 .
6. 设 分别是 的三条边,且 . 我们知道,如果 为直角三角形,那 么 (勾股定理). 反过来,如果 ,那么 为直角三角形 (勾股定理 的逆定理). 由此可知, 为直角三角形的充要条件是 .
请利用边长 分别给出 为锐角三角形和钝角三角形的一个充要条件,并证明.
新人教 A 版必修一 P35
11. 学校举办运动会时, 高一 (1) 班共有 28 名同学参加比赛, 有 15 人参加游泳比赛, 有 8 人参 加田径比赛, 有 14 人参加球类比赛, 同时参加游泳比赛和田径比赛的有 3 人, 同时参加游泳 比赛和球类比赛的有 3 人, 没有人同时参加三项比赛. 同时参加田径和球类比赛的有多少人 只参加游泳一项比赛的有多少人
12. 根据下述事实, 分别写出含有量词的全称量词命题或存在量词命题:
(第 12 (2) 题)
(1) ,
......
(2) 如图,在 中, 与 分别为 与 边上的高,则 与 所在的直线交于一点 .新人教 B 版必修一 P22
(1) 已知集合 ,且 ,求 的值.
(2) 已知集合 ,若 ,求 的取值范围.
(3) 已知 ,且 , 求 的取值范围.
(3) 已知 为全集 的非空真子集,且 与 不相等,若 , 试判断集合 和 的关系,并求出 .
新人教 B 版必修一 P31
(3) 已知区间 ,且 “ ” 是真命题,求实数 的取 值范围.
新人教 B 版必修一 P38
判断下列命题的真假:
(1) ; (2) .
(2) 判断下列命题的真假:
(1) ;
(2) .
新人教 B 版必修一 P42
1. 已知 ,求 中所含元素的个数.
2. 已知集合 , ,定义集合
求 中元素的个数.
3. 若 ,求 的值.
4. 若 ,求 的值.
5. 设 为全集, 是集合,判断 “存在集合 ,使得 ” 是 “ ” 的什么条件.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
