24.2与圆有关的位置关系综合训练题(人教新课标九年级上)
文档属性
| 名称 | 24.2与圆有关的位置关系综合训练题(人教新课标九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
圆第二单元24.2与圆有关的位置关系综合训练
一、选择题(本题共10小题,每题4分,共40分)
. (改编)三角形内切圆的圆心是( )
A.三个内角平分线的交点; B.三条边的中线的交点
C.三条边垂直平分线的交点 D.三边的三条高的交点
答案:A
. 下列命题不正确的是( )
A.经过一点的圆有无数个 B.经过两点的圆有无数个
C.经过不在同一条直线上的三个点确定一个圆 D.过四个点一定能作一个圆
答案:D
. (原创)⊙O的半径是6,圆心到直线的距离为3,则直线与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
答案:A
.(改编)如图,已知线段,⊙P与⊙Q的半径均为1cm.点分别从出发,在直线上按箭头所示方向运动.⊙P的速度是1米/秒,⊙Q的速度是2米/秒。当两点未相遇前,在下列选项中,⊙P与⊙Q不可能出现的位置关系是( )
A.外离 B.外切 C.相交 D.内含
答案:D
.(原创)如图,⊙O的半径OC=5cm,直线1⊥OC,垂足为H,且1交⊙O于A、B两点,AB=8cm,则1沿OC所在直线向上平移( )时与⊙O相切.
A.1cm B.2 cm C.3 cm D.8 cm
答案:D
.(2008年甘肃省兰州市)如图,在中,,
经过点且与边相切的动圆与分别相交于点
,则线段长度的最小值是( )
A. B.
C.5 D.4.8
答案:A
.半径分别为13和15的两圆相交,且公共弦长为24,则两圆的圆心距为( )
A.或 B.或 C. D.或
答案:D
. 半径分别为5和8的两个圆的圆心距 为,若3<≤13,则这两个圆的位置关系一定是( )
A相交 B.相切 C.外切或相交 D.内切或相交
答案:D
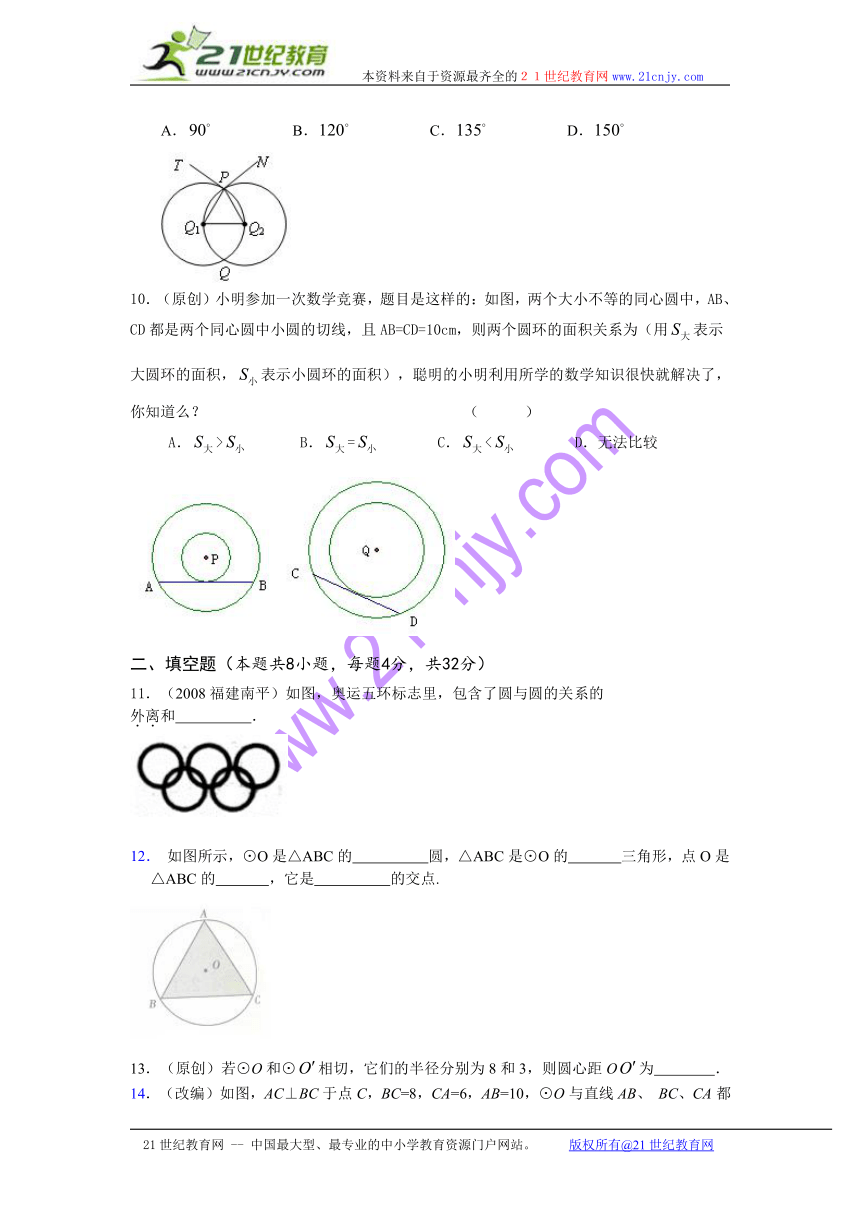
.如图,半径相等的两圆⊙O1,⊙O2相交于两点.圆心在⊙O2上,是⊙O1的切线,是⊙O2的切线,则的大小是( )
A. B. C. D.
答案:B
.(原创)小明参加一次数学竞赛,题目是这样的:如图,两个大小不等的同心圆中,AB、CD都是两个同心圆中小圆的切线,且AB=CD=10cm,则两个圆环的面积关系为(用表示大圆环的面积,表示小圆环的面积),聪明的小明利用所学的数学知识很快就解决了,你知道么? ( )
A.> B.= C.< D.无法比较
答案:B
二、填空题(本题共8小题,每题4分,共32分)
.(2008福建南平)如图,奥运五环标志里,包含了圆与圆的关系的
外离和 .
答案:相交或外离
. 如图所示,⊙O是△ABC的 圆,△ABC是⊙O的 三角形,点O是△ABC的 ,它是 的交点.
答案:外接, 内接 ,外心,三边的中垂线,65°
.(原创)若⊙O和⊙相切,它们的半径分别为8和3,则圆心距O为 .
答案: 11和5
.(改编)如图,AC⊥BC于点C,BC=8,CA=6,AB=10,⊙O与直线AB、 BC、CA都相切,则⊙O的半径等于 .
答案:4
.(原创)如图,⊙O内切于,切点分别为.已知,,连结,那么等于( )
A. B. C. D.
答案:B
.在直角坐标系中,⊙O的圆心在圆点,半径为3,⊙A的圆心A的坐标为(,1),半径为1,那么⊙O与⊙A的位置关系是 .
答案:内切
. 如图,,以为直径的圆与一个以5为半径的圆相切于点P,正方形ABCD的顶点A、B在大圆上,小圆在正方形的外部且与CD切于点Q.则 .
答案:6
.已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为l的⊙O与射线AC只有一个公共点,那么x的取值范围是 .
答案:或
三、实验题(本题共8小题,共48分)
.(6分)(改编)如图8,已知中,,AC=3,BC=4,已点C为圆心作,半径为.
(1) 当取什么值时,点AB与相切?
(2)当取什么值时, 内与斜边只有一个公共点?
答案:解:(1)当圆与斜边相切,如图 ∵∴
(2)由于,则以C为圆心,AC为半径的圆与AB交与A、B两点,如图,显然,当时,所作的圆与斜边AB只有一个公共点.
.(2008黄冈市)已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
求证:DE是⊙O的切线.
答案:解:BE与⊙O相切
理由:连接OB, ∵
∴ )
∵ ,∴ ,∴
又∵ ,∴ ,∴
即,∴ BE与⊙O相切
.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠A PB的度数.
答案:解:∵PA、PB切⊙O于A、B,
∴PA=PB ,∴OA ⊥PA .
∵∠OAB=25°,∴∠PAB=65°
∴∠APB=180-65°×2=50°.
.已知:如图,以△ABC的边为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
(1)与⊙O是否相切?请说明理由;
(2)当△ABC满足什么条件时,以点O,B,E,D为顶点的四边形是平行四边形?并说明理由.
答案:(1)与⊙O相切.
理由:连结,,切⊙O于,为直径,
,
又平分,,
.又,;
,即.
与⊙O相切.
(2)当为等腰直角三角形时,四边形是平行四边形.
是等腰直角三角形,
.
于,为中点.
,.
四边形是平行四边形.
.(改编)某乡薄铁社厂的王师傅要在长为25cm,宽为18cm的薄铁板上裁出一个最大的圆和两个尽可能大的小圆.他先画出了如图所示的草图,但他在求小圆半径时遇到了困难,请你帮助王师傅计算出这两个小圆的半径.
答案:连结 由题意得大圆的半径为9cm,设小圆的半径为r,在中可得 ,解得cm
.张宇同学是一名天文爱好者,他通过查阅资料得知:地球、火星的运行轨道可以近似地看成是以太阳为圆的两个同心圆,且这两个同心圆在同一平面上(如图所示).由于地球和火星的运行速度不同,所以二者的位置不断发生变化.当地球、太阳和火星三者处在一条直线上,且太阳位于地球、火星中间时,称为“合”;当地球、太阳和火星三者处在一条直线上,且地球于太阳与火星中间时,称为“冲”.另外,从地球上看火星与太阳,当两条视线互相垂直时,分别称为“东方照”和“西方照”.已知地球距太阳15(千万千米),火星距太阳20.5(千万千米).
(1)分别求“合”、“冲”、“东方照”、“西方照”时,地球与火星的距离(结果保留准确值).
(2)如果从地球上发射宇宙飞船登上火星,为了节省燃料,应选择在什么位置时发射较好,说明你的理由.
(注:从地球上看火星,火星在地球左、右两侧时分别叫做“东方照”、“西方照”.)
答案:解:(1)依题意可知“合”“冲”“东方照”“西方照”时分别 如下图(1)、(2)、(3)、(4)所示:
设O,A,B三点分别代表太阳,地球,火星.
“合”时,地球与火星之间的距离为AB=35.5(千万千米).
“冲”时,地球与火星之间的距离为AB=5.5(千万千米).
“东方照"时,地球与火星之间的距离为(千万千米).
同理可求“西方照”时,地球与火星之间的距离为(千万千米).
(2)从地球上发射宇宙飞船到火星,应选择在“冲”位置时,发射较好.
因为由(1)中的计算可知,此时地球离火星最近.
.如图,P为正比例函数图象上的一个动点,⊙P的半径为3,设点P的坐标为(,).
(1)求⊙P与直线相切时点P的坐标.
(2)请直接写出⊙P与直线相交、相离时的取值范围.
答案:(1)过点P作直线的垂线,垂足为A.
当点P在直线的右侧时,,P(5,).
当点P在直线的左侧时,,P(,).
∴当⊙P与直线相切时,点P的坐标为(5,)或(,).
(2)当时,⊙P与直线相交.
当或时,⊙P与直线相离.
.(10分)如图,是半径为的⊙O上的定点,动点从出发,以的速度沿圆周逆时针运动,当点回到地立即停止运动.
(1)如果,求点运动的时间;
(2)如果点是延长线上的一点,,那么当点运动的时间为时,判断直线与⊙O的位置关系,并说明理由.
与圆有关的位置关系综合训练
一、选择题(本题共10小题,每题4分,共40分)
1.A 2.D 3.A 4.D 5.D 6. D 7.D 8.D 9.B 10.B
二、填空题(本题共8小题,每题4分,共32分)
11.相交。
12.外接, 内接 ,外心,三边的中垂线,65°
13.11和5
14.4
15.B
16.内切
17.6
18.或
三、实验题(本题共8小题,共48分)
19.解:(1)当圆与斜边相切,如图 ∵∴
(2)由于,则以C为圆心,AC为半径的圆与AB交与A、B两点,如图,显然,当时,所作的圆与斜边AB只有一个公共点.
20.【答案】证明:连接OD,则OD=OB,
∴∠B=∠1.
∵AB=AC,
∴∠B=∠C,
∴∠1=∠C,
∴OD∥AC,
∴∠ODE=∠DEC.
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线.
21.解:如图,∵PA、PB切⊙O于A、B,
∴PA=PB ,∴OA ⊥PA .
∵∠OAB=25°,∴∠PAB=65°
∴∠APB=180-65°×2=50°.
22.(1)与⊙O相切.
理由:连结,,切⊙O于,为直径,
,
又平分,,
.又,;
,即.
与⊙O相切.
(2)当为等腰直角三角形时,四边形是平行四边形.
是等腰直角三角形,
.
于,为中点.
,.
四边形是平行四边形.
23.连结 由题意得大圆的半径为9cm,设小圆的半径为r,在中可得 ,解得cm
24.解:(1)依题意可知“合”“冲”“东方照”“西方照”时分别 如下图(1)、(2)、(3)、(4)所示:
设O,A,B三点分别代表太阳,地球,火星.
“合”时,地球与火星之间的距离为AB=35.5(千万千米).
“冲”时,地球与火星之间的距离为AB=5.5(千万千米).
“东方照"时,地球与火星之间的距离为(千万千米).
同理可求“西方照”时,地球与火星之间的距离为(千万千米).
(2)从地球上发射宇宙飞船到火星,应选择在“冲”位置时,发射较好.
因为由(1)中的计算可知,此时地球离火星最近.
25.(1)过点P作直线的垂线,垂足为A.
当点P在直线的右侧时,,P(5,).
当点P在直线的左侧时,,P(,).
∴当⊙P与直线相切时,点P的坐标为(5,)或(,).
(2)当时,⊙P与直线相交.
当或时,⊙P与直线相离.
26.解:设⊙O的半径为R,则OE=OD-DE=R-2. 在Rt△OEB中,由勾股定理得OE2+BE2=OB.2.即(R-2)2+42=R2.解得R=5.∴⊙O的半径为5.
如图,当点运动的时间为时,直线与⊙O相切.
理由如下:
当点运动的时间为时,点运动的路程为.
连接.∵⊙O的周长为,的长为⊙O周长的,. ,是等边三角形.,,,.,...直线与⊙O相切.
作者:马新华 山东省东营市利津县虎滩中学 257449答案:解:设⊙O的半径为R,则OE=OD-DE=R-2. 在Rt△OEB中,由勾股定理得OE2+BE2=OB.2.即(R-2)2+42=R2.解得R=5.∴⊙O的半径为5.
如图,当点运动的时间为时,直线与⊙O相切.
理由如下:
当点运动的时间为时,点运动的路程为.
连接.∵⊙O的周长为,的长为⊙O周长的,. ,是等边三角形.,,,.,...直线与⊙O相切.
B
C
E
F
A
·
P
A
B
O
图
A
P
B
O
·
P
A
B
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
圆第二单元24.2与圆有关的位置关系综合训练
一、选择题(本题共10小题,每题4分,共40分)
. (改编)三角形内切圆的圆心是( )
A.三个内角平分线的交点; B.三条边的中线的交点
C.三条边垂直平分线的交点 D.三边的三条高的交点
答案:A
. 下列命题不正确的是( )
A.经过一点的圆有无数个 B.经过两点的圆有无数个
C.经过不在同一条直线上的三个点确定一个圆 D.过四个点一定能作一个圆
答案:D
. (原创)⊙O的半径是6,圆心到直线的距离为3,则直线与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
答案:A
.(改编)如图,已知线段,⊙P与⊙Q的半径均为1cm.点分别从出发,在直线上按箭头所示方向运动.⊙P的速度是1米/秒,⊙Q的速度是2米/秒。当两点未相遇前,在下列选项中,⊙P与⊙Q不可能出现的位置关系是( )
A.外离 B.外切 C.相交 D.内含
答案:D
.(原创)如图,⊙O的半径OC=5cm,直线1⊥OC,垂足为H,且1交⊙O于A、B两点,AB=8cm,则1沿OC所在直线向上平移( )时与⊙O相切.
A.1cm B.2 cm C.3 cm D.8 cm
答案:D
.(2008年甘肃省兰州市)如图,在中,,
经过点且与边相切的动圆与分别相交于点
,则线段长度的最小值是( )
A. B.
C.5 D.4.8
答案:A
.半径分别为13和15的两圆相交,且公共弦长为24,则两圆的圆心距为( )
A.或 B.或 C. D.或
答案:D
. 半径分别为5和8的两个圆的圆心距 为,若3<≤13,则这两个圆的位置关系一定是( )
A相交 B.相切 C.外切或相交 D.内切或相交
答案:D
.如图,半径相等的两圆⊙O1,⊙O2相交于两点.圆心在⊙O2上,是⊙O1的切线,是⊙O2的切线,则的大小是( )
A. B. C. D.
答案:B
.(原创)小明参加一次数学竞赛,题目是这样的:如图,两个大小不等的同心圆中,AB、CD都是两个同心圆中小圆的切线,且AB=CD=10cm,则两个圆环的面积关系为(用表示大圆环的面积,表示小圆环的面积),聪明的小明利用所学的数学知识很快就解决了,你知道么? ( )
A.> B.= C.< D.无法比较
答案:B
二、填空题(本题共8小题,每题4分,共32分)
.(2008福建南平)如图,奥运五环标志里,包含了圆与圆的关系的
外离和 .
答案:相交或外离
. 如图所示,⊙O是△ABC的 圆,△ABC是⊙O的 三角形,点O是△ABC的 ,它是 的交点.
答案:外接, 内接 ,外心,三边的中垂线,65°
.(原创)若⊙O和⊙相切,它们的半径分别为8和3,则圆心距O为 .
答案: 11和5
.(改编)如图,AC⊥BC于点C,BC=8,CA=6,AB=10,⊙O与直线AB、 BC、CA都相切,则⊙O的半径等于 .
答案:4
.(原创)如图,⊙O内切于,切点分别为.已知,,连结,那么等于( )
A. B. C. D.
答案:B
.在直角坐标系中,⊙O的圆心在圆点,半径为3,⊙A的圆心A的坐标为(,1),半径为1,那么⊙O与⊙A的位置关系是 .
答案:内切
. 如图,,以为直径的圆与一个以5为半径的圆相切于点P,正方形ABCD的顶点A、B在大圆上,小圆在正方形的外部且与CD切于点Q.则 .
答案:6
.已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为l的⊙O与射线AC只有一个公共点,那么x的取值范围是 .
答案:或
三、实验题(本题共8小题,共48分)
.(6分)(改编)如图8,已知中,,AC=3,BC=4,已点C为圆心作,半径为.
(1) 当取什么值时,点AB与相切?
(2)当取什么值时, 内与斜边只有一个公共点?
答案:解:(1)当圆与斜边相切,如图 ∵∴
(2)由于,则以C为圆心,AC为半径的圆与AB交与A、B两点,如图,显然,当时,所作的圆与斜边AB只有一个公共点.
.(2008黄冈市)已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
求证:DE是⊙O的切线.
答案:解:BE与⊙O相切
理由:连接OB, ∵
∴ )
∵ ,∴ ,∴
又∵ ,∴ ,∴
即,∴ BE与⊙O相切
.如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠A PB的度数.
答案:解:∵PA、PB切⊙O于A、B,
∴PA=PB ,∴OA ⊥PA .
∵∠OAB=25°,∴∠PAB=65°
∴∠APB=180-65°×2=50°.
.已知:如图,以△ABC的边为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
(1)与⊙O是否相切?请说明理由;
(2)当△ABC满足什么条件时,以点O,B,E,D为顶点的四边形是平行四边形?并说明理由.
答案:(1)与⊙O相切.
理由:连结,,切⊙O于,为直径,
,
又平分,,
.又,;
,即.
与⊙O相切.
(2)当为等腰直角三角形时,四边形是平行四边形.
是等腰直角三角形,
.
于,为中点.
,.
四边形是平行四边形.
.(改编)某乡薄铁社厂的王师傅要在长为25cm,宽为18cm的薄铁板上裁出一个最大的圆和两个尽可能大的小圆.他先画出了如图所示的草图,但他在求小圆半径时遇到了困难,请你帮助王师傅计算出这两个小圆的半径.
答案:连结 由题意得大圆的半径为9cm,设小圆的半径为r,在中可得 ,解得cm
.张宇同学是一名天文爱好者,他通过查阅资料得知:地球、火星的运行轨道可以近似地看成是以太阳为圆的两个同心圆,且这两个同心圆在同一平面上(如图所示).由于地球和火星的运行速度不同,所以二者的位置不断发生变化.当地球、太阳和火星三者处在一条直线上,且太阳位于地球、火星中间时,称为“合”;当地球、太阳和火星三者处在一条直线上,且地球于太阳与火星中间时,称为“冲”.另外,从地球上看火星与太阳,当两条视线互相垂直时,分别称为“东方照”和“西方照”.已知地球距太阳15(千万千米),火星距太阳20.5(千万千米).
(1)分别求“合”、“冲”、“东方照”、“西方照”时,地球与火星的距离(结果保留准确值).
(2)如果从地球上发射宇宙飞船登上火星,为了节省燃料,应选择在什么位置时发射较好,说明你的理由.
(注:从地球上看火星,火星在地球左、右两侧时分别叫做“东方照”、“西方照”.)
答案:解:(1)依题意可知“合”“冲”“东方照”“西方照”时分别 如下图(1)、(2)、(3)、(4)所示:
设O,A,B三点分别代表太阳,地球,火星.
“合”时,地球与火星之间的距离为AB=35.5(千万千米).
“冲”时,地球与火星之间的距离为AB=5.5(千万千米).
“东方照"时,地球与火星之间的距离为(千万千米).
同理可求“西方照”时,地球与火星之间的距离为(千万千米).
(2)从地球上发射宇宙飞船到火星,应选择在“冲”位置时,发射较好.
因为由(1)中的计算可知,此时地球离火星最近.
.如图,P为正比例函数图象上的一个动点,⊙P的半径为3,设点P的坐标为(,).
(1)求⊙P与直线相切时点P的坐标.
(2)请直接写出⊙P与直线相交、相离时的取值范围.
答案:(1)过点P作直线的垂线,垂足为A.
当点P在直线的右侧时,,P(5,).
当点P在直线的左侧时,,P(,).
∴当⊙P与直线相切时,点P的坐标为(5,)或(,).
(2)当时,⊙P与直线相交.
当或时,⊙P与直线相离.
.(10分)如图,是半径为的⊙O上的定点,动点从出发,以的速度沿圆周逆时针运动,当点回到地立即停止运动.
(1)如果,求点运动的时间;
(2)如果点是延长线上的一点,,那么当点运动的时间为时,判断直线与⊙O的位置关系,并说明理由.
与圆有关的位置关系综合训练
一、选择题(本题共10小题,每题4分,共40分)
1.A 2.D 3.A 4.D 5.D 6. D 7.D 8.D 9.B 10.B
二、填空题(本题共8小题,每题4分,共32分)
11.相交。
12.外接, 内接 ,外心,三边的中垂线,65°
13.11和5
14.4
15.B
16.内切
17.6
18.或
三、实验题(本题共8小题,共48分)
19.解:(1)当圆与斜边相切,如图 ∵∴
(2)由于,则以C为圆心,AC为半径的圆与AB交与A、B两点,如图,显然,当时,所作的圆与斜边AB只有一个公共点.
20.【答案】证明:连接OD,则OD=OB,
∴∠B=∠1.
∵AB=AC,
∴∠B=∠C,
∴∠1=∠C,
∴OD∥AC,
∴∠ODE=∠DEC.
∵DE⊥AC,
∴∠DEC=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线.
21.解:如图,∵PA、PB切⊙O于A、B,
∴PA=PB ,∴OA ⊥PA .
∵∠OAB=25°,∴∠PAB=65°
∴∠APB=180-65°×2=50°.
22.(1)与⊙O相切.
理由:连结,,切⊙O于,为直径,
,
又平分,,
.又,;
,即.
与⊙O相切.
(2)当为等腰直角三角形时,四边形是平行四边形.
是等腰直角三角形,
.
于,为中点.
,.
四边形是平行四边形.
23.连结 由题意得大圆的半径为9cm,设小圆的半径为r,在中可得 ,解得cm
24.解:(1)依题意可知“合”“冲”“东方照”“西方照”时分别 如下图(1)、(2)、(3)、(4)所示:
设O,A,B三点分别代表太阳,地球,火星.
“合”时,地球与火星之间的距离为AB=35.5(千万千米).
“冲”时,地球与火星之间的距离为AB=5.5(千万千米).
“东方照"时,地球与火星之间的距离为(千万千米).
同理可求“西方照”时,地球与火星之间的距离为(千万千米).
(2)从地球上发射宇宙飞船到火星,应选择在“冲”位置时,发射较好.
因为由(1)中的计算可知,此时地球离火星最近.
25.(1)过点P作直线的垂线,垂足为A.
当点P在直线的右侧时,,P(5,).
当点P在直线的左侧时,,P(,).
∴当⊙P与直线相切时,点P的坐标为(5,)或(,).
(2)当时,⊙P与直线相交.
当或时,⊙P与直线相离.
26.解:设⊙O的半径为R,则OE=OD-DE=R-2. 在Rt△OEB中,由勾股定理得OE2+BE2=OB.2.即(R-2)2+42=R2.解得R=5.∴⊙O的半径为5.
如图,当点运动的时间为时,直线与⊙O相切.
理由如下:
当点运动的时间为时,点运动的路程为.
连接.∵⊙O的周长为,的长为⊙O周长的,. ,是等边三角形.,,,.,...直线与⊙O相切.
作者:马新华 山东省东营市利津县虎滩中学 257449答案:解:设⊙O的半径为R,则OE=OD-DE=R-2. 在Rt△OEB中,由勾股定理得OE2+BE2=OB.2.即(R-2)2+42=R2.解得R=5.∴⊙O的半径为5.
如图,当点运动的时间为时,直线与⊙O相切.
理由如下:
当点运动的时间为时,点运动的路程为.
连接.∵⊙O的周长为,的长为⊙O周长的,. ,是等边三角形.,,,.,...直线与⊙O相切.
B
C
E
F
A
·
P
A
B
O
图
A
P
B
O
·
P
A
B
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
