小学数学人教版五年级上方程的意义教案
文档属性
| 名称 | 小学数学人教版五年级上方程的意义教案 |  | |
| 格式 | docx | ||
| 文件大小 | 869.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 16:55:14 | ||
图片预览


文档简介
方程的意义
教学目标:
1.在自主探索的过程中,理解与掌握方程的意义,弄清方程和等式两个概念的关系。
2.培养学生认真观察、思考分析问题的能力。发展学生思维的灵活性。
3.加强数学知识与现实世界的联系,有利于培养学生的数学应用意识。培养学生认真观察、善于思考的学习习惯,渗透转化的数学思想。
教学重点:
理解与掌握方程的意义。
教学难点:
帮助学生建立“方程”的概念,并会应用。
教具学具准备:课件
教学过程:
一、视频导入
师:在课前,武老师给大家准备了一段动画短片,我们一起来看一看。——播放《爆笑虫子翘翘板》
师:一短片里的虫子为什么最后都跑到右边,而不往左边跑?
生:因为怕被吃掉。
所以虫子跑到右边是为了使……
师:其实我们生活中还有很多工具跟跷跷板的平衡原理是相似(出示课件变换——天平)
二、借助直观,初识等量关系,感知方程意义
1.师:这是什么?关于天平,你有哪些了解?
让学生畅所欲言。比如:天平可以称物体的重量。当天平两边物体的重量一样时,天平就平衡了。同学们的课外知识可真丰富。武老师给大家简单介绍一下:介绍3部分
鼓励表扬学生知识面广后,(出示法徽图片)这是我们国家的法徽,它是由麦穗、齿轮、华表、天平等构成,其中天平寓意公平公正,作为小学生的我们,更要做一个诚实守信正直的人。
出示平衡的天平。
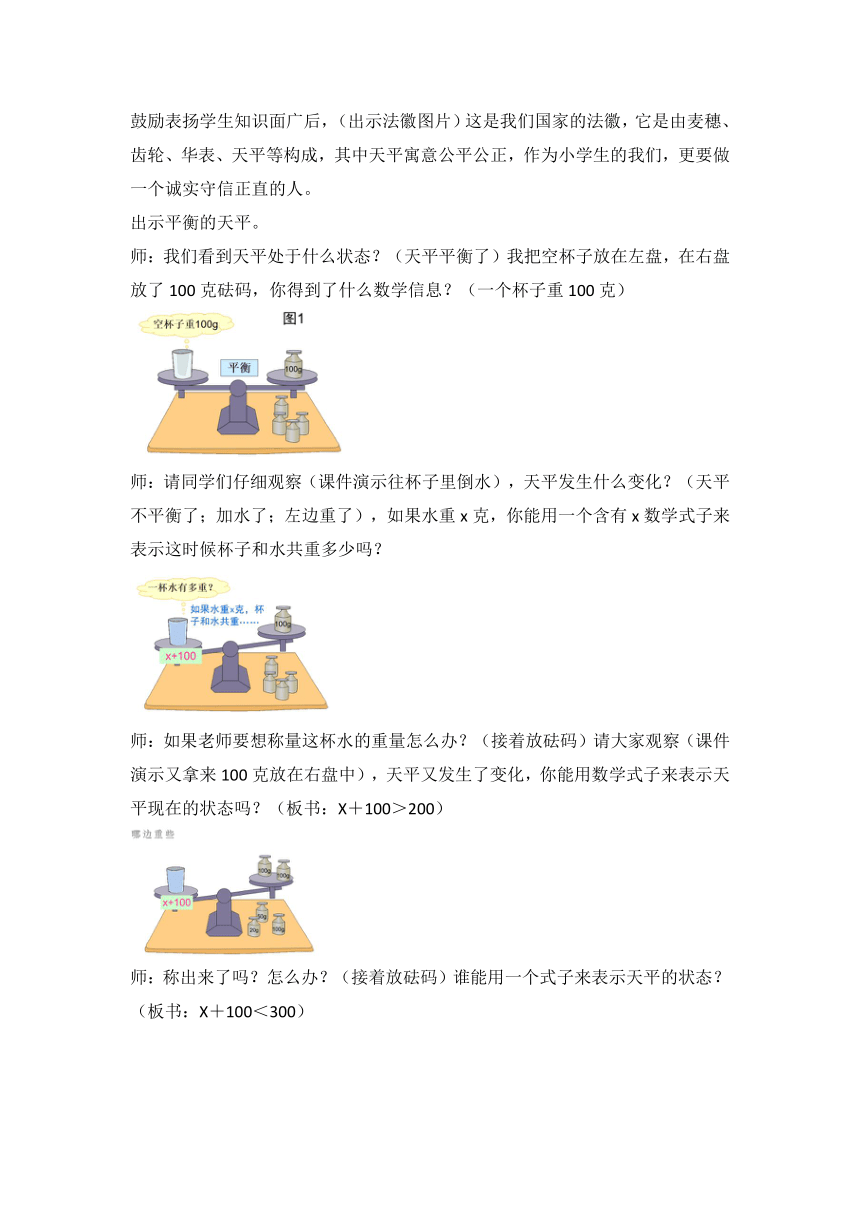
师:我们看到天平处于什么状态?(天平平衡了)我把空杯子放在左盘,在右盘放了100克砝码,你得到了什么数学信息?(一个杯子重100克)
师:请同学们仔细观察(课件演示往杯子里倒水),天平发生什么变化?(天平不平衡了;加水了;左边重了),如果水重x克,你能用一个含有x数学式子来表示这时候杯子和水共重多少吗?
师:如果老师要想称量这杯水的重量怎么办?(接着放砝码)请大家观察(课件演示又拿来100克放在右盘中),天平又发生了变化,你能用数学式子来表示天平现在的状态吗?(板书:X+100>200)
师:称出来了吗?怎么办?(接着放砝码)谁能用一个式子来表示天平的状态?(板书:X+100<300)
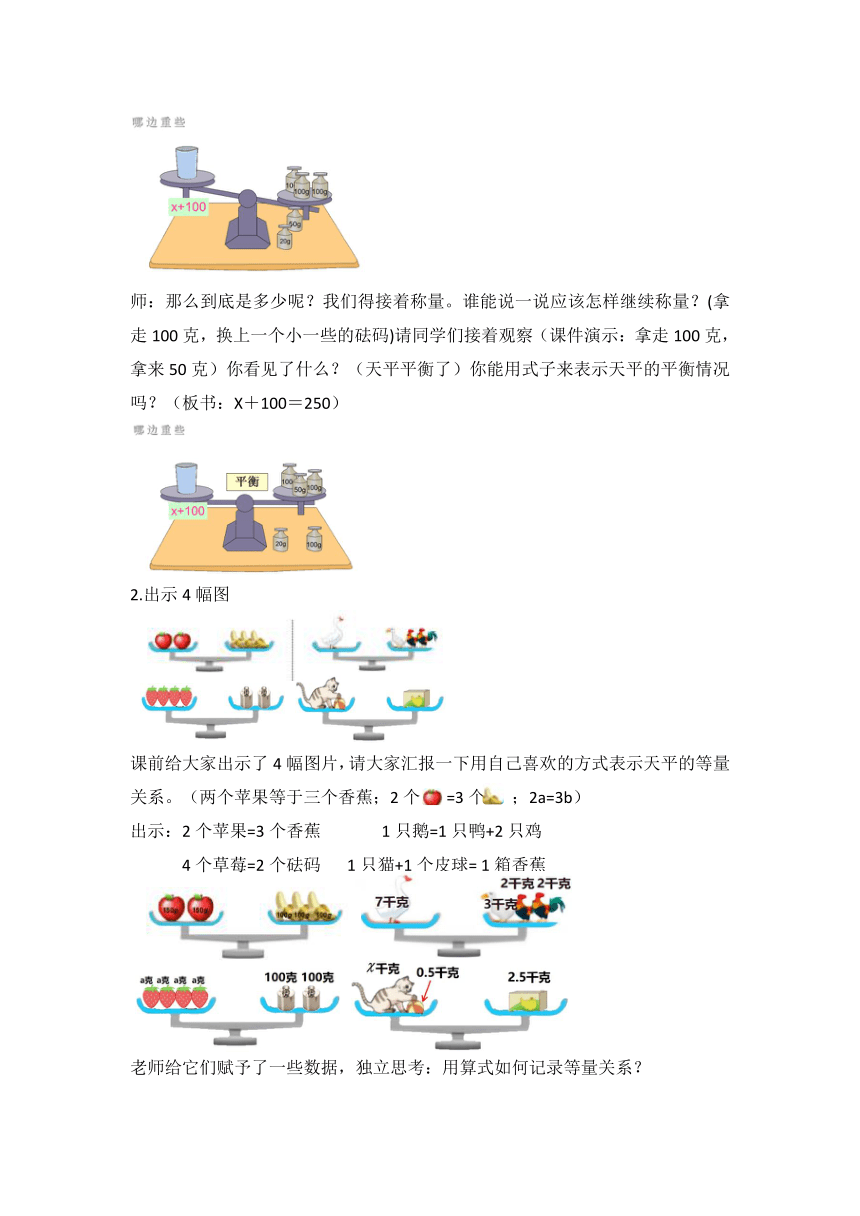
师:那么到底是多少呢?我们得接着称量。谁能说一说应该怎样继续称量?(拿走100克,换上一个小一些的砝码)请同学们接着观察(课件演示:拿走100克,拿来50克)你看见了什么?(天平平衡了)你能用式子来表示天平的平衡情况吗?(板书:X+100=250)
2.出示4幅图
课前给大家出示了4幅图片,请大家汇报一下用自己喜欢的方式表示天平的等量关系。(两个苹果等于三个香蕉;2个 =3个 ;2a=3b)
出示:2个苹果=3个香蕉 1只鹅=1只鸭+2只鸡
4个草莓=2个砝码 1只猫+1个皮球= 1箱香蕉
老师给它们赋予了一些数据,独立思考:用算式如何记录等量关系?
板书:2×150=3×100 7=3+2×2 4x=100+100 x+0.5=2.5
师:大家用这么简单的数学式子就能表示出那么复杂的生活情景,你们真了不起!
3.引导分类,构建概念
师:通过刚才试验,我们得出了几个式子。如果我们对这几个式子分类,可以分成几类呢?请同学们先独立思考,再和小组内的同学说一说这几个式子可以分成几类?是按什么标准分类的?
小组汇报。
预设1:按是否含有未知数可以分为两类:3+2×2=7,2×150=3×100为一类,X+100=250、X+100>200、X+100<300、x+0.5=2.5、4x=100+100为一类;
预设2:按是否是等式可以分为两类2×150=3×100、X+100=250、4x=100+100、3+2×2=7为一类,X+100>200、X+100<300为一类。
师:什么是等式?(带“等号”的式子表示了出来)这些带等号的式子在数学上叫等式。
师:还有其他分类了么?那再请同学们把这些等式分分类(分成两类:有未知数,没有未知数。)
师:如果你是这些式子,你会作自我介绍,说一说你的特点吗?(学生回答给予评价,并加以补充)
师:像X+100=250这样由未知数参与,描述等量关系的等式叫做方程。也就是含有未知数的等式,我们把它叫做方程。今天我们学习的就是方程的意义。(板书课题)
师:既然含有未知数的等式是方程,那方程和等式之间有怎样的关系呢?小组里说一说,用图表示它们的关系。学生总结方程与等式之间的关系。(方程一定是等式,等式不一定是方程。)板书关系
师:看来大家已经掌握了方程的意义,以及方程和等式的关系,你能自己试着写几个方程吗?在你的学案上试着写写。学生写完后作答。
师:老师这有几个式子,它们是方程吗?请大家快速判断一下(课件)
你们判断的这么快,是有什么小窍门么?
根据方程和等式的关系,请你将序号填到相应的圆圈中。
结合情境,提炼等量关系,感悟方程模型思想。
通过天平平衡情况列出等式和方程,如果没有天平了,在你的心中把这个线段图转化成天平的形式
1、出示线段图:
思考:说一说等量关系。还有其他的等量关系么?
(红色+绿色=蓝色;蓝色-红色=绿色;蓝色-绿色=红色)
出示数据:
学生汇报等量关系(已看页数+未看页数=总页数;总页数-已看页数=未看页数;总页数-未看页数=已看页数)
出示:学案出示这四幅图,用方程表示线段图中的等量关系,写一写,比比谁的方法多。
学生汇报多种方法
(第一幅图:x+22=15+y;第二幅图:9x=18;18÷9=x;18÷x=9;第三幅图:(5+x)×2=36;36÷2=5+x;36÷2-5=x;36÷2-x=5;第四幅图:6+4=3y+1;3y+1-6=4;3y+1-4=6;6+4-3y=1;(6+4-1)÷3=y;(6+4-1)÷y=3;2y=6;6÷2=y;6÷y=2;y+1=44-1=y;4-y=1)
出示四幅图
小结:同学们真厉害,把这么复杂的情境和图,通过一个简单的方程就能清楚的呈现出他们之间的等量关系,老师给你们点赞。(在一般情况下我们不单独把未知数放在方程的一侧,这种方程其实就是我们以前的算术方法。)
结合前测,探究复杂情境,体会方程顺向思维的优越性和必要性
出示前测单:
桌上有15个苹果,①桔子比苹果的3倍还多3个,桔子多少个?
②苹果比桔子的3倍还少3个,桔子有多少个?
出示前测分析表:
在课前进行了前测,老师看到大家第一题写得都很不错,但在写第二题时就有点困难,那我们还是借助线段图找等量关系来解决它。
对比思辨:为什么第2题正确率低?难在哪里?
讨论交流:说一说两道题的等量关系。
1.桔子比苹果的3倍还多3个,把苹果看作一倍数,列出等量关系式苹果×3+3=桔子 ,当苹果数量为15时,列出算式为?(15×3+3)
2.苹果比桔子的3倍少3个,把桔子看作一倍数,列出等量关系式?桔子×3-3=苹果 ,把桔子看作x,能不能列一个方程?3x-3=15;很多同学采用算术法,苹果是桔子的3倍么?怎样才能正好是桔子的三倍,苹果的数量加上少的3个正好是桔子的三倍,谁来描述一下等量关系。(苹果+3)÷3=桔子。当苹果数量为15时,列算式((15+3)÷3)(在课堂上,学生列式时喜欢用算术法,此时要注意对比两种等量关系的思考过程,使学生体会到方程的便捷)
关键思考问题:第2题哪个等量关系更容易思考?为什么?
小结:方程更好思考,便捷
五、方程史话,课堂小结
知识拓展,了解“方程史话”
学好数学,为国家建设添砖加瓦。
共同回顾小结。
数学学习是需要积累经验的,这节课我们经历了从数学故事——等量关系——方程的学习过程,学习了这节课,你对方程有了哪些新的认识?学习方程有什么作用呢?这些方程中的未知数是多少呢?该怎么求呢?看来还需要进一步研究。
教学目标:
1.在自主探索的过程中,理解与掌握方程的意义,弄清方程和等式两个概念的关系。
2.培养学生认真观察、思考分析问题的能力。发展学生思维的灵活性。
3.加强数学知识与现实世界的联系,有利于培养学生的数学应用意识。培养学生认真观察、善于思考的学习习惯,渗透转化的数学思想。
教学重点:
理解与掌握方程的意义。
教学难点:
帮助学生建立“方程”的概念,并会应用。
教具学具准备:课件
教学过程:
一、视频导入
师:在课前,武老师给大家准备了一段动画短片,我们一起来看一看。——播放《爆笑虫子翘翘板》
师:一短片里的虫子为什么最后都跑到右边,而不往左边跑?
生:因为怕被吃掉。
所以虫子跑到右边是为了使……
师:其实我们生活中还有很多工具跟跷跷板的平衡原理是相似(出示课件变换——天平)
二、借助直观,初识等量关系,感知方程意义
1.师:这是什么?关于天平,你有哪些了解?
让学生畅所欲言。比如:天平可以称物体的重量。当天平两边物体的重量一样时,天平就平衡了。同学们的课外知识可真丰富。武老师给大家简单介绍一下:介绍3部分
鼓励表扬学生知识面广后,(出示法徽图片)这是我们国家的法徽,它是由麦穗、齿轮、华表、天平等构成,其中天平寓意公平公正,作为小学生的我们,更要做一个诚实守信正直的人。
出示平衡的天平。
师:我们看到天平处于什么状态?(天平平衡了)我把空杯子放在左盘,在右盘放了100克砝码,你得到了什么数学信息?(一个杯子重100克)
师:请同学们仔细观察(课件演示往杯子里倒水),天平发生什么变化?(天平不平衡了;加水了;左边重了),如果水重x克,你能用一个含有x数学式子来表示这时候杯子和水共重多少吗?
师:如果老师要想称量这杯水的重量怎么办?(接着放砝码)请大家观察(课件演示又拿来100克放在右盘中),天平又发生了变化,你能用数学式子来表示天平现在的状态吗?(板书:X+100>200)
师:称出来了吗?怎么办?(接着放砝码)谁能用一个式子来表示天平的状态?(板书:X+100<300)
师:那么到底是多少呢?我们得接着称量。谁能说一说应该怎样继续称量?(拿走100克,换上一个小一些的砝码)请同学们接着观察(课件演示:拿走100克,拿来50克)你看见了什么?(天平平衡了)你能用式子来表示天平的平衡情况吗?(板书:X+100=250)
2.出示4幅图
课前给大家出示了4幅图片,请大家汇报一下用自己喜欢的方式表示天平的等量关系。(两个苹果等于三个香蕉;2个 =3个 ;2a=3b)
出示:2个苹果=3个香蕉 1只鹅=1只鸭+2只鸡
4个草莓=2个砝码 1只猫+1个皮球= 1箱香蕉
老师给它们赋予了一些数据,独立思考:用算式如何记录等量关系?
板书:2×150=3×100 7=3+2×2 4x=100+100 x+0.5=2.5
师:大家用这么简单的数学式子就能表示出那么复杂的生活情景,你们真了不起!
3.引导分类,构建概念
师:通过刚才试验,我们得出了几个式子。如果我们对这几个式子分类,可以分成几类呢?请同学们先独立思考,再和小组内的同学说一说这几个式子可以分成几类?是按什么标准分类的?
小组汇报。
预设1:按是否含有未知数可以分为两类:3+2×2=7,2×150=3×100为一类,X+100=250、X+100>200、X+100<300、x+0.5=2.5、4x=100+100为一类;
预设2:按是否是等式可以分为两类2×150=3×100、X+100=250、4x=100+100、3+2×2=7为一类,X+100>200、X+100<300为一类。
师:什么是等式?(带“等号”的式子表示了出来)这些带等号的式子在数学上叫等式。
师:还有其他分类了么?那再请同学们把这些等式分分类(分成两类:有未知数,没有未知数。)
师:如果你是这些式子,你会作自我介绍,说一说你的特点吗?(学生回答给予评价,并加以补充)
师:像X+100=250这样由未知数参与,描述等量关系的等式叫做方程。也就是含有未知数的等式,我们把它叫做方程。今天我们学习的就是方程的意义。(板书课题)
师:既然含有未知数的等式是方程,那方程和等式之间有怎样的关系呢?小组里说一说,用图表示它们的关系。学生总结方程与等式之间的关系。(方程一定是等式,等式不一定是方程。)板书关系
师:看来大家已经掌握了方程的意义,以及方程和等式的关系,你能自己试着写几个方程吗?在你的学案上试着写写。学生写完后作答。
师:老师这有几个式子,它们是方程吗?请大家快速判断一下(课件)
你们判断的这么快,是有什么小窍门么?
根据方程和等式的关系,请你将序号填到相应的圆圈中。
结合情境,提炼等量关系,感悟方程模型思想。
通过天平平衡情况列出等式和方程,如果没有天平了,在你的心中把这个线段图转化成天平的形式
1、出示线段图:
思考:说一说等量关系。还有其他的等量关系么?
(红色+绿色=蓝色;蓝色-红色=绿色;蓝色-绿色=红色)
出示数据:
学生汇报等量关系(已看页数+未看页数=总页数;总页数-已看页数=未看页数;总页数-未看页数=已看页数)
出示:学案出示这四幅图,用方程表示线段图中的等量关系,写一写,比比谁的方法多。
学生汇报多种方法
(第一幅图:x+22=15+y;第二幅图:9x=18;18÷9=x;18÷x=9;第三幅图:(5+x)×2=36;36÷2=5+x;36÷2-5=x;36÷2-x=5;第四幅图:6+4=3y+1;3y+1-6=4;3y+1-4=6;6+4-3y=1;(6+4-1)÷3=y;(6+4-1)÷y=3;2y=6;6÷2=y;6÷y=2;y+1=44-1=y;4-y=1)
出示四幅图
小结:同学们真厉害,把这么复杂的情境和图,通过一个简单的方程就能清楚的呈现出他们之间的等量关系,老师给你们点赞。(在一般情况下我们不单独把未知数放在方程的一侧,这种方程其实就是我们以前的算术方法。)
结合前测,探究复杂情境,体会方程顺向思维的优越性和必要性
出示前测单:
桌上有15个苹果,①桔子比苹果的3倍还多3个,桔子多少个?
②苹果比桔子的3倍还少3个,桔子有多少个?
出示前测分析表:
在课前进行了前测,老师看到大家第一题写得都很不错,但在写第二题时就有点困难,那我们还是借助线段图找等量关系来解决它。
对比思辨:为什么第2题正确率低?难在哪里?
讨论交流:说一说两道题的等量关系。
1.桔子比苹果的3倍还多3个,把苹果看作一倍数,列出等量关系式苹果×3+3=桔子 ,当苹果数量为15时,列出算式为?(15×3+3)
2.苹果比桔子的3倍少3个,把桔子看作一倍数,列出等量关系式?桔子×3-3=苹果 ,把桔子看作x,能不能列一个方程?3x-3=15;很多同学采用算术法,苹果是桔子的3倍么?怎样才能正好是桔子的三倍,苹果的数量加上少的3个正好是桔子的三倍,谁来描述一下等量关系。(苹果+3)÷3=桔子。当苹果数量为15时,列算式((15+3)÷3)(在课堂上,学生列式时喜欢用算术法,此时要注意对比两种等量关系的思考过程,使学生体会到方程的便捷)
关键思考问题:第2题哪个等量关系更容易思考?为什么?
小结:方程更好思考,便捷
五、方程史话,课堂小结
知识拓展,了解“方程史话”
学好数学,为国家建设添砖加瓦。
共同回顾小结。
数学学习是需要积累经验的,这节课我们经历了从数学故事——等量关系——方程的学习过程,学习了这节课,你对方程有了哪些新的认识?学习方程有什么作用呢?这些方程中的未知数是多少呢?该怎么求呢?看来还需要进一步研究。
