期末模拟预测卷(含答案)2023-2024学年数学五年级下册青岛版
文档属性
| 名称 | 期末模拟预测卷(含答案)2023-2024学年数学五年级下册青岛版 |  | |
| 格式 | docx | ||
| 文件大小 | 488.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 11:32:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末模拟预测卷(试题)2023-2024学年数学五年级下册青岛版
一、选择题
1.一瓶矿泉水大约( )。
A.500mL B.2500立方厘米 C.60mL D.10L
2.把一个棱长为3cm的正方体切成棱长为1cm的小正方体,可以切成( )块。
A.9 B.18 C.27 D.36
3.如果比较两个城市一周气温变化的情况,采用( )统计图比较合适。
A.折线 B.复式折线 C.条形 D.复式条形
4.两个数的最大公因数是4,最小公倍数是24,这两个数可能是( )。
A.8和24 B.8和12 C.16和24 D.12和24
5.下面分数中,分数单位最大的一个数是( )。
A. B. C. D.
6.用12分米长的铁丝制作一个正方体框架。如果不考虑损耗,做成的正方体框架的棱长是( )。
A.3分米 B.2分米 C.12厘米 D.10厘米
二、填空题
7.一种方便面包装袋上标着“净重105±5g”,这种方便面最重是( )。
8.一块橡皮的体积大约是8( ),冰箱的容积是220( )。
9.5.05立方分米=( )毫升 4500升=( )立方米
10.一个长方体是由24个棱长1厘米的小正方体拼成,从一个方向观察这个长方体最多能同时看到( )个面,这个长方体的体积是( )立方厘米。
11.淘气生日时爸爸花了120元定制了一盒生日蛋糕,淘气先分给爸爸吃了其中的,分给妈妈吃的和爸爸一样多,那么这块蛋糕还剩下没吃。
12.一个长方体,如果高增加5厘米,就变成棱长为8厘来的正方体。原长方体的体积是( )。
三、判断题
13.长方体是特殊的正方体。( )
14.一个数,如果不是负数,必定就是正数。( )
15.一个分数的分母越大,它的分数单位就越大。( )
16.数对(4,5)和(5,4)表示的位置是一样的。( )
17.的分子加上16,要使分数的大小不变,分母应该加上16。( )
四、计算题
18.直接写得数。
19.能简算的要简算。
20.解方程。
+x=1 x- x+
21.求下面组合图形的体积。(单位:米)
五、解答题
22.“做彩粽”是端午节的一项传统手工活动。小玲做了两个彩粽,做第一个彩粽用了小时,做第二个彩粽比第一个少用了小时,小玲做这两个彩粽一共用了多少小时?
23.学校庆祝“六一”儿童节举行了书画展。以下三位同学对展区情况进行了布置。
你认为展区还有展示其他作品的位置吗?
24.新学期,五年级一班竞选班委。经过第一轮选举,选出奇奇、毛毛、贝贝、丫丫、豆豆5人。如果从他们5人中选出2人担任正、副班长,会有多少种不同的选法?
25.黄豆中富含蛋白质、淀粉、脂肪及其他营养成分。1千克黄豆中,蛋白质的含量是千克,淀粉和脂肪的含量是千克,其他营养成分的含量是多少千克?
26.数学课上,同学们策划设计用一块长24厘米,宽16厘米的长方形铁皮,在四个角上各剪去一个小正方形(如图所示),做成一个无盖的长方体储物盒。林林和小强分别设计了不同的方案,林林选择边长为3厘米,小强选择边长为4厘米。他们两个谁的方案做成的长方体储物盒容积最大?
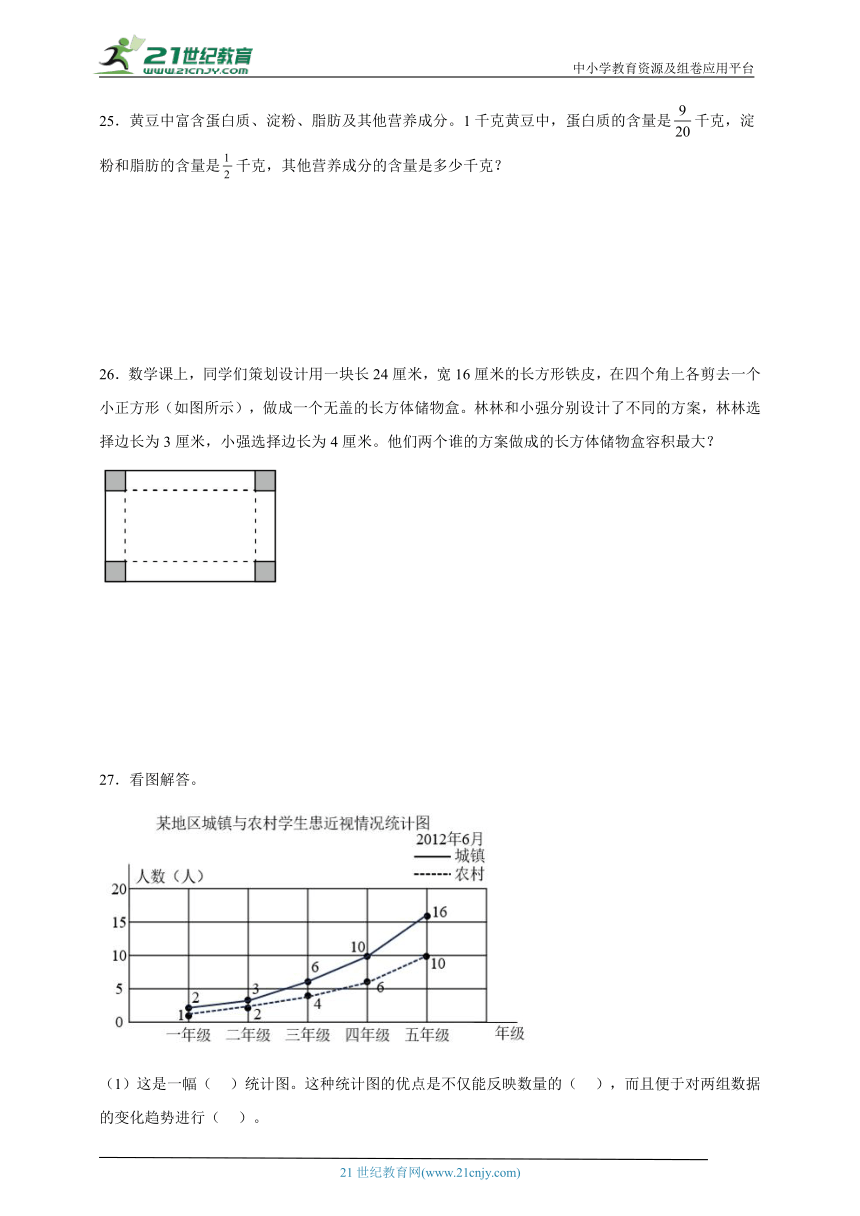
27.看图解答。
(1)这是一幅( )统计图。这种统计图的优点是不仅能反映数量的( ),而且便于对两组数据的变化趋势进行( )。
(2)从图中可以看出该地区城镇和农村学生患近视人数都呈( )趋势。
(3)你还发现了什么?
参考答案:
1.A
【分析】1升=1000毫升=1000立方厘米,依据生活实例进行数据的判断。
【详解】A.一瓶矿泉水大约是500毫升,符合生活实际,判断正确;
B.2500立方厘米=2500毫升,超大桶可乐的容积大概是2500毫升,不符合瓶装矿泉水的规格,判断错误;
C.一瓶眼药水大概是15毫升,60毫升相当于4瓶眼药水,不符合瓶装矿泉水的规格,判断错误;
D.10升是大桶生活饮用水的规格,不符合瓶装矿泉水的规格,判断错误。
一瓶矿泉水大约500mL。
故答案为:A
【点睛】此题考查学生对于容积单位的认识,结合生活实际分析是解题的关键。
2.C
【分析】先根据正方体的体积=棱长×棱长×棱长,分别求出大正方体和小正方体的体积,再用大正方体的体积除以小正方体的体积,即可求出可以切的块数。
【详解】(3×3×3)÷(1×1×1)
=27÷1
=27(块)
可以切成27块。
故答案为:C
【点睛】本题考查正方体体积公式的实际应用。
3.B
【分析】折线统计图可以体现具体数据的大小以及数据的增减变化,条形统计图可以体现具体数据的大小,据此结合题干分析。
【详解】想体现天气的变化情况应该选择折线统计图,因为想比较两个城市的气温变化,则应该选择复式折线统计图。
故答案为:B
【点睛】掌握统计图表示数据的特点是解题的关键。
4.B
【分析】最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此可设这两个数分别是4x,4y,x和y互质,且4xy=24,据此求出xy的积,进而推出x和y的值,最后推出这两个数。据此解答。
【详解】设这两个数分别是4x,4y,
4xy=24
解:4xy÷4=24÷4
xy=6
6=2×3
2×4=8
3×4=12
两个数的最大公因数是4,最小公倍数是24,这两个数可能是8和12。
故答案为:B
【点睛】本题考查了最大公因数和最小公倍数的认识和应用。
5.B
【分析】根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。分数比较大小:分子相同,分母较大的分数比较小,分母较小的分数比较大;所以分母越小,分数单位越大。
【详解】的分数单位是,的分数单位是,的分数单位是,的分数单位是;
<<<
所以分数单位最大的一个数是。
故答案为:B
【点睛】本题主要考查了分数单位的认识以及分数比较大小的方法。
6.D
【分析】由“正方体的棱长和=棱长×12”可推导出:棱长=正方体的棱长和÷12。根据题意可知:正方体的棱长和是12分米,用12÷12即可求出这个正方体框架的棱长。
【详解】12÷12=1(分米)
1分米=10厘米
所以做成的正方体框架的棱长是10厘米。
故答案为:D
【点睛】明确正方体的12条棱的长度都相等是解决此题的关键。。
7.110g
【分析】首先要弄清“净重105±5g”的含义,也就是说这种方便面标准的重量是105g,实际每袋最多不超过(105+5)g,最少必须不低于(105-5)g,据此解答。
【详解】105+5=110(g)
所以一种方便面包装袋上标着“净重105±5g”,这种方便面最重是110g。
【点睛】解答本题的关键是要知道以105克为标准,超出标准的为正,低于标准的为负。
8. 立方厘米/cm3 升/L
【分析】常用的体积单位有立方米、立方分米、立方厘米,常用的容积单位有升和毫升,根据实际情况结合单位的大小选择合适的计量单位即可。
【详解】根据实际情况可知:
一块橡皮的体积大约是8立方厘米;
冰箱的容积大约是220升。
【点睛】此题考查了根据情景选择合适的体积、容积单位,要学会联系生活实际灵活选择。
9. 5050 4.5
【分析】1毫升=1立方厘米,1立方分米=1000立方厘米;1升=1立方分米,1立方米=1000立方分米,据此解答。
【详解】5.05×1000=5050立方厘米
5050立方厘米=5050毫升
4500升=4500立方分米
4500立方分米=4.5立方米
所以5.05立方分米=5050毫升,4500升=4.5立方米。
【点睛】解答本题的关键是掌握单位换算的方法,即把高级单位换算成低级单位时,用乘法乘它们之间的进率,把低级单位换算成高级单位时,用除法除以它们之间的进率。
10. 3 24
【分析】根据观察范围随着观察点、观察角度的变化而变化,从一个方向观察长方体或正方体,最多能看到它的3个面:前面、上(或下)面、一个侧面;小正方体的体积可根据正方体的体积公式求出,长方体是由24个小正方体组合而成,用小正方体的体积乘24,即可求出长方体的体积,据此解答。
【详解】1×1×1×24=24(立方厘米)
即从一个方向观察这个长方体最多能同时看到3个面,这个长方体的体积是24立方厘米。
【点睛】此题考查了从不同方向观察物体、正方体的体积公式以及立体图形的拼搭。
11.
【分析】将这个生日蛋糕看作一个整体,爸爸和妈妈都吃了,根据分数的加减法,列式:1--=,求出这个蛋糕还剩下的部分。
【详解】1--=
则这块蛋糕还剩下没吃。
【点睛】本题主要考查的是分数的加减法运算,计算过程要细心认真。
12.192立方厘米/192cm3
【分析】据题意,长方体,高增加5厘米,就变成棱长为8厘来的正方体,由此可知,原来的长方体的长和宽都是8厘米,高是8-5=3厘米,再根据长方体的体积=长×宽×高,代入数据即可解答。
【详解】由分析可知:
8-5=3(厘米)
8×8×3
=64×3
=192(立方厘米)
所以,原长方体的体积是192立方厘米。
【点睛】本题考查长方体的体积,熟练掌握长方体的体积计算公式是解题的关键。
13.×
【分析】根据正方体的特征,长、宽、高都相等的长方体叫做正方体,正方体是特殊的长方体,正方体一定是长方体,长方体不一定是正方体,长方体包含正方体,据此解答。
【详解】根据分析,正方体是特殊的长方体,可以用下图表示正方体和长方体的关系:
所以原题的说法错误。
故答案为:×
【点睛】此题考查了长方体、正方体的特征以及它们之间的联系。
14.×
【分析】比0大的数是正数,比0小的数是负数,0既不是正数,也不是负数,据此分析。
【详解】0既不是正数,也不是负数,所以原题说法错误。
故答案为:×
【点睛】关键是理解正负数的含义。
15.×
【分析】把单位“1”平均分成若干份,表示其中1份的数是分数单位;一个分数的分母越大,分成的份数就越多,每一份就越小,即分数单位就越小。
【详解】一个分数的分母越大,它的分数单位就越小。
故答案为:×
【点睛】掌握分数单位的意义是解题的关键。
16.×
【分析】根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此进行判断即可。
【详解】由分析可知:
(4,5)表示第4列,第5行;(5,4)表示第5列,第4行,所以数对(4,5)和(5,4)表示的位置是不一样的。原题干说法错误。
故答案为:×
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
17.×
【分析】把的分子加上16后,分子变为20,相当于分子乘5,根据分数的基本性质,分数的分子、分母同时乘或除以同一个不为0的数,分数的大小不变;所以要使分数的大小不变,分母也应该乘5,这时分母变为25,再减去原来的数5,即可得到分母应增加的数。
【详解】4+16=20
20÷4=5
所以分母也应该乘5。
或者增加:
5×5-5
=25-5
=20
即分母应该加20。
故答案为:×
【点睛】此题的解题关键是灵活运用分数的基本性质求解。
18.1;;;;0;
;;;;
【详解】略
19.4;0;
【分析】(1)运用减法的性质进行计算即可;
(2)去括号后,按照从左到右的运算顺序进行计算即可;
(3)运用加法结合律进行计算即可。
【详解】
=
=
=4
=
=
=0
=
=
=
20.x=;x=;x=
【分析】(1)根据等式的性质1,方程左右两边同时减去,解出方程;
(2)根据等式的性质1,方程左右两边同时加,解出方程;
(3)根据等式的性质1,方程左右两边同时减去,解出方程。
【详解】(1)+x=1
解:+x-=1-
x=
(2)x-
解:x-
x
x=
(3)x+
解:x+
x
x=
21.1512平方米
【分析】根据正方体的体积公式:V=a3,代入棱长的数据,求出正方体的体积,再根据长方体的体积公式:V=abh,代入数据,求出长方体的体积,再把正方体的体积和长方体的体积加起来,即可得出组合图形的体积。
【详解】
(平方米)
22.小时
【分析】根据题意可知,做第一个彩粽用的时间减去小时等于做第二个彩粽用的时间,据此用-即可求出做第二个彩粽用的时间,再加上做第一个彩粽用的时间,即可求出一共花的时间。
【详解】-+
=+
=(小时)
答:小玲做这两个彩粽一共用了小时。
【点睛】本题考查了异分母分数加减法的混合运算和应用,掌握相应的计算方法是解答本题的关键。
23.还有展示其他作品的位置
【分析】把展区看作单位“1”,根据分数加法的意义,用++即可求出书法、国画和素描作品占展区的几分之几,如果小于1,则说明展区还有其他作品的位置。如果等于1,则说明没有其他作品的位置。
【详解】++
=+
=
<1
答:展区还有展示其他作品的位置。
【点睛】本题主要考查了异分母分数加法的计算和应用,掌握相应的计算方法是解答本题的关键。
24.20种
【分析】如果有一个人是奇奇,那么另外一个人可能是毛毛、贝贝、丫丫、豆豆,有4种情况;如果有一个人是毛毛,那么另一个人可能是贝贝、丫丫、豆豆,有3种情况;如果有一个人是贝贝,那么另外一个人可能是丫丫、豆豆,有2种情况;如果有一个人是丫丫,那么另外一个人可能是豆豆,有1种情况;共4+3+2+1=10种情况,选中的两人不一定谁是正班长,谁是副班长,再用10×2即可求出选法的数量。
【详解】(4+3+2+1)×2
=10×2
=20(种)
答:会有20种不同的选法。
【点睛】解决问题的关键在于避免重复,也可以采用列举法将选法列举出来。
25.千克
【分析】根据减法的意义,用黄豆的重量减去蛋白质、淀粉和脂肪的含量即可求出其他营养成分的含量是多少千克。
【详解】
=
=(千克)
答:其他营养成分的含量是千克。
【点睛】本题考查异分母分数减法,明确其计算方法是解题的关键。
26.林林
【分析】通过观察图形可知:折成的无盖长方体储物盒的长是(24-小正方形的边长×2)厘米,宽是(16-小正方形的边长×2)厘米,高是小正方形的边长。把储物盒的长、宽、高相乘,即可求出储物盒的容积。据此分别求出林林和小强设计的储物盒的容积,再比较大小即可。
【详解】林林:(24-3×2)×(16-3×2)×3
=(24-6)×(16-6)×3
=18×10×3
=540(立方厘米)
小强:(24-4×2)×(16-4×2)×4
=(24-8)×(16-8)×4
=16×8×4
=512(立方厘米)
540>512
答:林林的方案做成的长方体储物盒容积最大。
【点睛】用长方形铁皮或正方形铁皮制成盒子(四个角上分别去掉一个相同的小正方形),盒子的长和宽要在铁皮的长和宽中去掉两个小正方形的边长,盒子的高是铁皮四个角去掉的小正方形的边长。
27.(1)复式折线;多少;比较
(2)上升
(3)城镇近视学生比农村近视学生多
【分析】(1)折线统计图用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
(2)折线往上表示上升趋势,折线往下表示下降趋势。
(3)答案不唯一,合理即可。
【详解】(1)这是一幅复式折线统计图。这种统计图的优点是不仅能反映数量的多少,而且便于对两组数据的变化趋势进行比较。
(2)从图中可以看出该地区城镇和农村学生患近视人数都呈上升趋势。
(3)答案不唯一,如从图中可以发现城镇近视学生比农村近视学生多。
【点睛】关键是熟悉折线统计图的特点,根据折线统计图的特点进行分析。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟预测卷(试题)2023-2024学年数学五年级下册青岛版
一、选择题
1.一瓶矿泉水大约( )。
A.500mL B.2500立方厘米 C.60mL D.10L
2.把一个棱长为3cm的正方体切成棱长为1cm的小正方体,可以切成( )块。
A.9 B.18 C.27 D.36
3.如果比较两个城市一周气温变化的情况,采用( )统计图比较合适。
A.折线 B.复式折线 C.条形 D.复式条形
4.两个数的最大公因数是4,最小公倍数是24,这两个数可能是( )。
A.8和24 B.8和12 C.16和24 D.12和24
5.下面分数中,分数单位最大的一个数是( )。
A. B. C. D.
6.用12分米长的铁丝制作一个正方体框架。如果不考虑损耗,做成的正方体框架的棱长是( )。
A.3分米 B.2分米 C.12厘米 D.10厘米
二、填空题
7.一种方便面包装袋上标着“净重105±5g”,这种方便面最重是( )。
8.一块橡皮的体积大约是8( ),冰箱的容积是220( )。
9.5.05立方分米=( )毫升 4500升=( )立方米
10.一个长方体是由24个棱长1厘米的小正方体拼成,从一个方向观察这个长方体最多能同时看到( )个面,这个长方体的体积是( )立方厘米。
11.淘气生日时爸爸花了120元定制了一盒生日蛋糕,淘气先分给爸爸吃了其中的,分给妈妈吃的和爸爸一样多,那么这块蛋糕还剩下没吃。
12.一个长方体,如果高增加5厘米,就变成棱长为8厘来的正方体。原长方体的体积是( )。
三、判断题
13.长方体是特殊的正方体。( )
14.一个数,如果不是负数,必定就是正数。( )
15.一个分数的分母越大,它的分数单位就越大。( )
16.数对(4,5)和(5,4)表示的位置是一样的。( )
17.的分子加上16,要使分数的大小不变,分母应该加上16。( )
四、计算题
18.直接写得数。
19.能简算的要简算。
20.解方程。
+x=1 x- x+
21.求下面组合图形的体积。(单位:米)
五、解答题
22.“做彩粽”是端午节的一项传统手工活动。小玲做了两个彩粽,做第一个彩粽用了小时,做第二个彩粽比第一个少用了小时,小玲做这两个彩粽一共用了多少小时?
23.学校庆祝“六一”儿童节举行了书画展。以下三位同学对展区情况进行了布置。
你认为展区还有展示其他作品的位置吗?
24.新学期,五年级一班竞选班委。经过第一轮选举,选出奇奇、毛毛、贝贝、丫丫、豆豆5人。如果从他们5人中选出2人担任正、副班长,会有多少种不同的选法?
25.黄豆中富含蛋白质、淀粉、脂肪及其他营养成分。1千克黄豆中,蛋白质的含量是千克,淀粉和脂肪的含量是千克,其他营养成分的含量是多少千克?
26.数学课上,同学们策划设计用一块长24厘米,宽16厘米的长方形铁皮,在四个角上各剪去一个小正方形(如图所示),做成一个无盖的长方体储物盒。林林和小强分别设计了不同的方案,林林选择边长为3厘米,小强选择边长为4厘米。他们两个谁的方案做成的长方体储物盒容积最大?
27.看图解答。
(1)这是一幅( )统计图。这种统计图的优点是不仅能反映数量的( ),而且便于对两组数据的变化趋势进行( )。
(2)从图中可以看出该地区城镇和农村学生患近视人数都呈( )趋势。
(3)你还发现了什么?
参考答案:
1.A
【分析】1升=1000毫升=1000立方厘米,依据生活实例进行数据的判断。
【详解】A.一瓶矿泉水大约是500毫升,符合生活实际,判断正确;
B.2500立方厘米=2500毫升,超大桶可乐的容积大概是2500毫升,不符合瓶装矿泉水的规格,判断错误;
C.一瓶眼药水大概是15毫升,60毫升相当于4瓶眼药水,不符合瓶装矿泉水的规格,判断错误;
D.10升是大桶生活饮用水的规格,不符合瓶装矿泉水的规格,判断错误。
一瓶矿泉水大约500mL。
故答案为:A
【点睛】此题考查学生对于容积单位的认识,结合生活实际分析是解题的关键。
2.C
【分析】先根据正方体的体积=棱长×棱长×棱长,分别求出大正方体和小正方体的体积,再用大正方体的体积除以小正方体的体积,即可求出可以切的块数。
【详解】(3×3×3)÷(1×1×1)
=27÷1
=27(块)
可以切成27块。
故答案为:C
【点睛】本题考查正方体体积公式的实际应用。
3.B
【分析】折线统计图可以体现具体数据的大小以及数据的增减变化,条形统计图可以体现具体数据的大小,据此结合题干分析。
【详解】想体现天气的变化情况应该选择折线统计图,因为想比较两个城市的气温变化,则应该选择复式折线统计图。
故答案为:B
【点睛】掌握统计图表示数据的特点是解题的关键。
4.B
【分析】最大公因数是两个数的公有的质因数的乘积,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积,据此可设这两个数分别是4x,4y,x和y互质,且4xy=24,据此求出xy的积,进而推出x和y的值,最后推出这两个数。据此解答。
【详解】设这两个数分别是4x,4y,
4xy=24
解:4xy÷4=24÷4
xy=6
6=2×3
2×4=8
3×4=12
两个数的最大公因数是4,最小公倍数是24,这两个数可能是8和12。
故答案为:B
【点睛】本题考查了最大公因数和最小公倍数的认识和应用。
5.B
【分析】根据分数单位的意义,把单位“1”平均分成若干份,表示其中1份的数叫分数单位。分数比较大小:分子相同,分母较大的分数比较小,分母较小的分数比较大;所以分母越小,分数单位越大。
【详解】的分数单位是,的分数单位是,的分数单位是,的分数单位是;
<<<
所以分数单位最大的一个数是。
故答案为:B
【点睛】本题主要考查了分数单位的认识以及分数比较大小的方法。
6.D
【分析】由“正方体的棱长和=棱长×12”可推导出:棱长=正方体的棱长和÷12。根据题意可知:正方体的棱长和是12分米,用12÷12即可求出这个正方体框架的棱长。
【详解】12÷12=1(分米)
1分米=10厘米
所以做成的正方体框架的棱长是10厘米。
故答案为:D
【点睛】明确正方体的12条棱的长度都相等是解决此题的关键。。
7.110g
【分析】首先要弄清“净重105±5g”的含义,也就是说这种方便面标准的重量是105g,实际每袋最多不超过(105+5)g,最少必须不低于(105-5)g,据此解答。
【详解】105+5=110(g)
所以一种方便面包装袋上标着“净重105±5g”,这种方便面最重是110g。
【点睛】解答本题的关键是要知道以105克为标准,超出标准的为正,低于标准的为负。
8. 立方厘米/cm3 升/L
【分析】常用的体积单位有立方米、立方分米、立方厘米,常用的容积单位有升和毫升,根据实际情况结合单位的大小选择合适的计量单位即可。
【详解】根据实际情况可知:
一块橡皮的体积大约是8立方厘米;
冰箱的容积大约是220升。
【点睛】此题考查了根据情景选择合适的体积、容积单位,要学会联系生活实际灵活选择。
9. 5050 4.5
【分析】1毫升=1立方厘米,1立方分米=1000立方厘米;1升=1立方分米,1立方米=1000立方分米,据此解答。
【详解】5.05×1000=5050立方厘米
5050立方厘米=5050毫升
4500升=4500立方分米
4500立方分米=4.5立方米
所以5.05立方分米=5050毫升,4500升=4.5立方米。
【点睛】解答本题的关键是掌握单位换算的方法,即把高级单位换算成低级单位时,用乘法乘它们之间的进率,把低级单位换算成高级单位时,用除法除以它们之间的进率。
10. 3 24
【分析】根据观察范围随着观察点、观察角度的变化而变化,从一个方向观察长方体或正方体,最多能看到它的3个面:前面、上(或下)面、一个侧面;小正方体的体积可根据正方体的体积公式求出,长方体是由24个小正方体组合而成,用小正方体的体积乘24,即可求出长方体的体积,据此解答。
【详解】1×1×1×24=24(立方厘米)
即从一个方向观察这个长方体最多能同时看到3个面,这个长方体的体积是24立方厘米。
【点睛】此题考查了从不同方向观察物体、正方体的体积公式以及立体图形的拼搭。
11.
【分析】将这个生日蛋糕看作一个整体,爸爸和妈妈都吃了,根据分数的加减法,列式:1--=,求出这个蛋糕还剩下的部分。
【详解】1--=
则这块蛋糕还剩下没吃。
【点睛】本题主要考查的是分数的加减法运算,计算过程要细心认真。
12.192立方厘米/192cm3
【分析】据题意,长方体,高增加5厘米,就变成棱长为8厘来的正方体,由此可知,原来的长方体的长和宽都是8厘米,高是8-5=3厘米,再根据长方体的体积=长×宽×高,代入数据即可解答。
【详解】由分析可知:
8-5=3(厘米)
8×8×3
=64×3
=192(立方厘米)
所以,原长方体的体积是192立方厘米。
【点睛】本题考查长方体的体积,熟练掌握长方体的体积计算公式是解题的关键。
13.×
【分析】根据正方体的特征,长、宽、高都相等的长方体叫做正方体,正方体是特殊的长方体,正方体一定是长方体,长方体不一定是正方体,长方体包含正方体,据此解答。
【详解】根据分析,正方体是特殊的长方体,可以用下图表示正方体和长方体的关系:
所以原题的说法错误。
故答案为:×
【点睛】此题考查了长方体、正方体的特征以及它们之间的联系。
14.×
【分析】比0大的数是正数,比0小的数是负数,0既不是正数,也不是负数,据此分析。
【详解】0既不是正数,也不是负数,所以原题说法错误。
故答案为:×
【点睛】关键是理解正负数的含义。
15.×
【分析】把单位“1”平均分成若干份,表示其中1份的数是分数单位;一个分数的分母越大,分成的份数就越多,每一份就越小,即分数单位就越小。
【详解】一个分数的分母越大,它的分数单位就越小。
故答案为:×
【点睛】掌握分数单位的意义是解题的关键。
16.×
【分析】根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此进行判断即可。
【详解】由分析可知:
(4,5)表示第4列,第5行;(5,4)表示第5列,第4行,所以数对(4,5)和(5,4)表示的位置是不一样的。原题干说法错误。
故答案为:×
【点睛】本题考查用数对表示位置,明确用数对表示位置的方法是解题的关键。
17.×
【分析】把的分子加上16后,分子变为20,相当于分子乘5,根据分数的基本性质,分数的分子、分母同时乘或除以同一个不为0的数,分数的大小不变;所以要使分数的大小不变,分母也应该乘5,这时分母变为25,再减去原来的数5,即可得到分母应增加的数。
【详解】4+16=20
20÷4=5
所以分母也应该乘5。
或者增加:
5×5-5
=25-5
=20
即分母应该加20。
故答案为:×
【点睛】此题的解题关键是灵活运用分数的基本性质求解。
18.1;;;;0;
;;;;
【详解】略
19.4;0;
【分析】(1)运用减法的性质进行计算即可;
(2)去括号后,按照从左到右的运算顺序进行计算即可;
(3)运用加法结合律进行计算即可。
【详解】
=
=
=4
=
=
=0
=
=
=
20.x=;x=;x=
【分析】(1)根据等式的性质1,方程左右两边同时减去,解出方程;
(2)根据等式的性质1,方程左右两边同时加,解出方程;
(3)根据等式的性质1,方程左右两边同时减去,解出方程。
【详解】(1)+x=1
解:+x-=1-
x=
(2)x-
解:x-
x
x=
(3)x+
解:x+
x
x=
21.1512平方米
【分析】根据正方体的体积公式:V=a3,代入棱长的数据,求出正方体的体积,再根据长方体的体积公式:V=abh,代入数据,求出长方体的体积,再把正方体的体积和长方体的体积加起来,即可得出组合图形的体积。
【详解】
(平方米)
22.小时
【分析】根据题意可知,做第一个彩粽用的时间减去小时等于做第二个彩粽用的时间,据此用-即可求出做第二个彩粽用的时间,再加上做第一个彩粽用的时间,即可求出一共花的时间。
【详解】-+
=+
=(小时)
答:小玲做这两个彩粽一共用了小时。
【点睛】本题考查了异分母分数加减法的混合运算和应用,掌握相应的计算方法是解答本题的关键。
23.还有展示其他作品的位置
【分析】把展区看作单位“1”,根据分数加法的意义,用++即可求出书法、国画和素描作品占展区的几分之几,如果小于1,则说明展区还有其他作品的位置。如果等于1,则说明没有其他作品的位置。
【详解】++
=+
=
<1
答:展区还有展示其他作品的位置。
【点睛】本题主要考查了异分母分数加法的计算和应用,掌握相应的计算方法是解答本题的关键。
24.20种
【分析】如果有一个人是奇奇,那么另外一个人可能是毛毛、贝贝、丫丫、豆豆,有4种情况;如果有一个人是毛毛,那么另一个人可能是贝贝、丫丫、豆豆,有3种情况;如果有一个人是贝贝,那么另外一个人可能是丫丫、豆豆,有2种情况;如果有一个人是丫丫,那么另外一个人可能是豆豆,有1种情况;共4+3+2+1=10种情况,选中的两人不一定谁是正班长,谁是副班长,再用10×2即可求出选法的数量。
【详解】(4+3+2+1)×2
=10×2
=20(种)
答:会有20种不同的选法。
【点睛】解决问题的关键在于避免重复,也可以采用列举法将选法列举出来。
25.千克
【分析】根据减法的意义,用黄豆的重量减去蛋白质、淀粉和脂肪的含量即可求出其他营养成分的含量是多少千克。
【详解】
=
=(千克)
答:其他营养成分的含量是千克。
【点睛】本题考查异分母分数减法,明确其计算方法是解题的关键。
26.林林
【分析】通过观察图形可知:折成的无盖长方体储物盒的长是(24-小正方形的边长×2)厘米,宽是(16-小正方形的边长×2)厘米,高是小正方形的边长。把储物盒的长、宽、高相乘,即可求出储物盒的容积。据此分别求出林林和小强设计的储物盒的容积,再比较大小即可。
【详解】林林:(24-3×2)×(16-3×2)×3
=(24-6)×(16-6)×3
=18×10×3
=540(立方厘米)
小强:(24-4×2)×(16-4×2)×4
=(24-8)×(16-8)×4
=16×8×4
=512(立方厘米)
540>512
答:林林的方案做成的长方体储物盒容积最大。
【点睛】用长方形铁皮或正方形铁皮制成盒子(四个角上分别去掉一个相同的小正方形),盒子的长和宽要在铁皮的长和宽中去掉两个小正方形的边长,盒子的高是铁皮四个角去掉的小正方形的边长。
27.(1)复式折线;多少;比较
(2)上升
(3)城镇近视学生比农村近视学生多
【分析】(1)折线统计图用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
(2)折线往上表示上升趋势,折线往下表示下降趋势。
(3)答案不唯一,合理即可。
【详解】(1)这是一幅复式折线统计图。这种统计图的优点是不仅能反映数量的多少,而且便于对两组数据的变化趋势进行比较。
(2)从图中可以看出该地区城镇和农村学生患近视人数都呈上升趋势。
(3)答案不唯一,如从图中可以发现城镇近视学生比农村近视学生多。
【点睛】关键是熟悉折线统计图的特点,根据折线统计图的特点进行分析。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
