期末模拟测试卷(含答案)2023-2024学年数学五年级下册北师大版
文档属性
| 名称 | 期末模拟测试卷(含答案)2023-2024学年数学五年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 698.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-06 14:43:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末模拟测试卷(试题)2023-2024学年数学五年级下册北师大版
一、选择题
1.一台冰箱的容积约是150( )。
A.cm3 B.L C.mL D.m3
2.下列算式中,计算结果最大的是( )。
A. B. C. D.
3.如图,把一段长方体的木料锯成3个完全相同的小正方体后,3个小正方体的表面积之和比原长方体的表面积增加了( )。
A.25 B.50 C.100 D.200
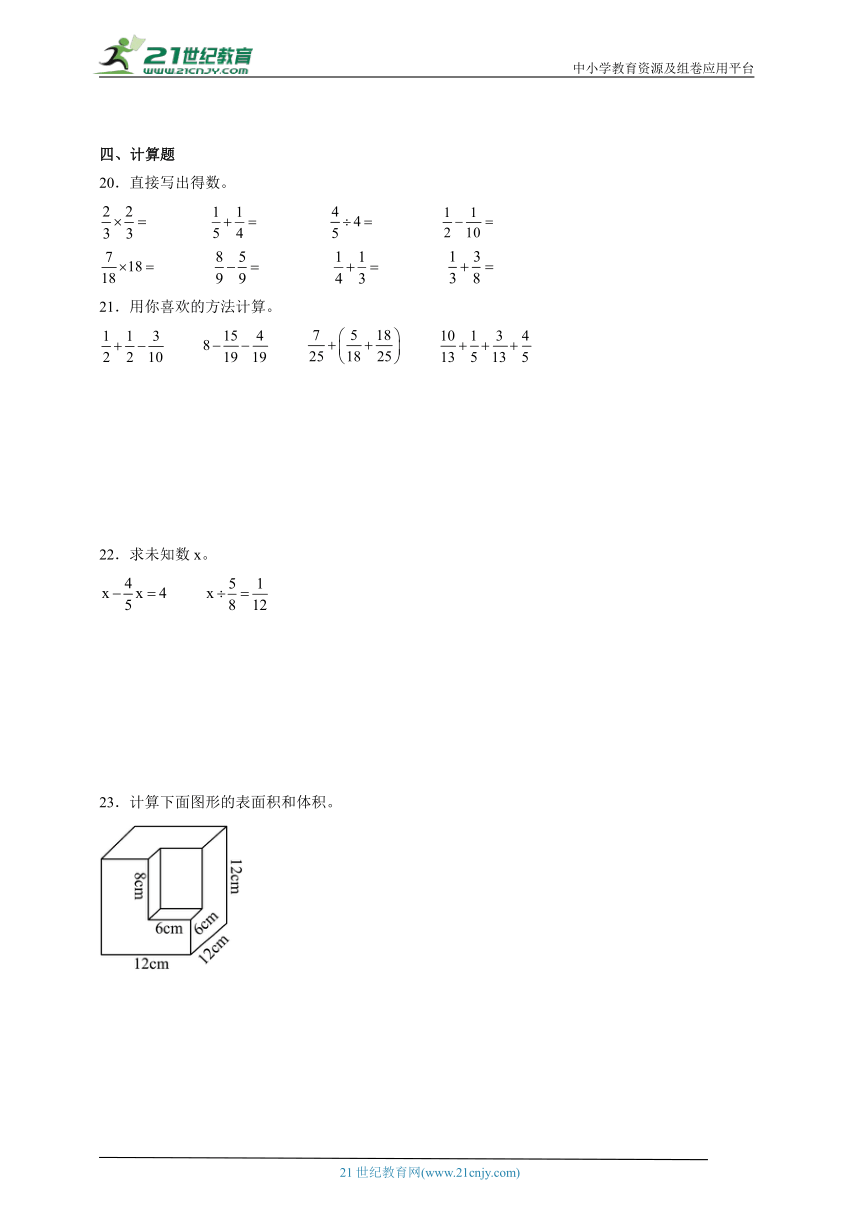
4.镇安大板栗以个大色润、甜脆可口、颗粒饱满、营养丰富、品质独特而闻名全国,被誉为“中国板栗之乡”。如图是一个正方体的平面展开图,则原正方体中,与“中”字所在的面相对的面上的字是( )。
A.板 B.栗 C.之 D.乡
5.操场上有8个小朋友在做游戏,他们的年龄分别是7岁、7岁、7岁、8岁、8岁、8岁、9岁、9岁,笑笑算了一下这些小朋友的平均年龄为7.875岁。下面( )种情况对做游戏人的平均年龄影响最大。
A.一位年龄45岁的老师加入游戏 B.5位年龄为7岁的小朋友加入游戏
C.8位年龄为8岁的小朋友加入游戏 D.两位9岁的小朋友离开游戏队伍
6.工厂计划本月生产一批零件。实际生产时发现上半月完成计划的,下半月完成计划的,下面说法正确的是( )。
A.本月生产计划没有完成 B.本月实际产量是计划的
C.本月实际产量超过计划的 D.本月产量超过计划的主要原因是上半月生产效率高
二、填空题
7.妙妙家买来一桶食用油,每天做菜约用这桶油的,7天大约用了这桶油的,还剩( )。
8.民二小学成立了合唱团和舞蹈队。其中参加舞蹈队的有18人,是合唱团人数的,参加合唱团的有( )人。
9.5个相加的和是( ),1时的是( )分,( )米的是米。
10.在( )里填上“>”“<”或“=”。
( ) ( ) ( )
11.一个正方体的棱长是5dm,它的表面积是( ),体积是( )。
12.为有效落实国家“双减”政策,加强学校特色建设,丰富学生校园文化生活,光明小学开展了丰富多彩的社团活动。其中棋艺社团有象棋、跳棋共26副,恰好可供120个学生同时进行活动,象棋2人下一副棋,跳棋6人下一副,有( )副象棋和( )副跳棋。
13.一个长方体的长、宽、高分别是6厘米、5厘米和3厘米,它的体积是( ) 。
14.如果,那么A+B=( )。
三、判断题
15.平均数能够代表一组数据的平均水平,任何一个数有变化,平均数都有反应。( )
16.一双运动鞋打八折销售是240元,求这双运动鞋的原价。列式为。( )
17.若学校在少年宫北偏西30°方向上,则少年宫在学校南偏东60°方向上。( )
18.如图,以服务中心为观测点,喷泉的位置是北偏东,距离服务中心150m。( )
19.两根一样长的绳子,第一根截去全长的,第二根截去米,两根剩下的绳子一样长。( )
四、计算题
20.直接写出得数。
21.用你喜欢的方法计算。
22.求未知数x。
23.计算下面图形的表面积和体积。
五、解答题
24.甲、乙两辆汽车从相距450千米的两地同时出发,相向而行。甲车速度是70千米/时,乙车的速度是80千米/时,几时后两车相遇?
25.阳光小学六年级女生的人数比全年级人数的少5人,男生人数比全年级人数的多16人,求全年级共有多少人?
26.张叔叔的农场共1200公顷,其中果园的面积占了农场的,种植香蕉的面积占了果园的,张叔叔的农场种植香蕉的面积是多少公顷?
27.一堆黄土如图所示,已知A的面积是25平方米,B的面积是15平方米,A处比B处高4米,现在把A处的土推向B处,使A、B两处同样高。A处下降了多少米?
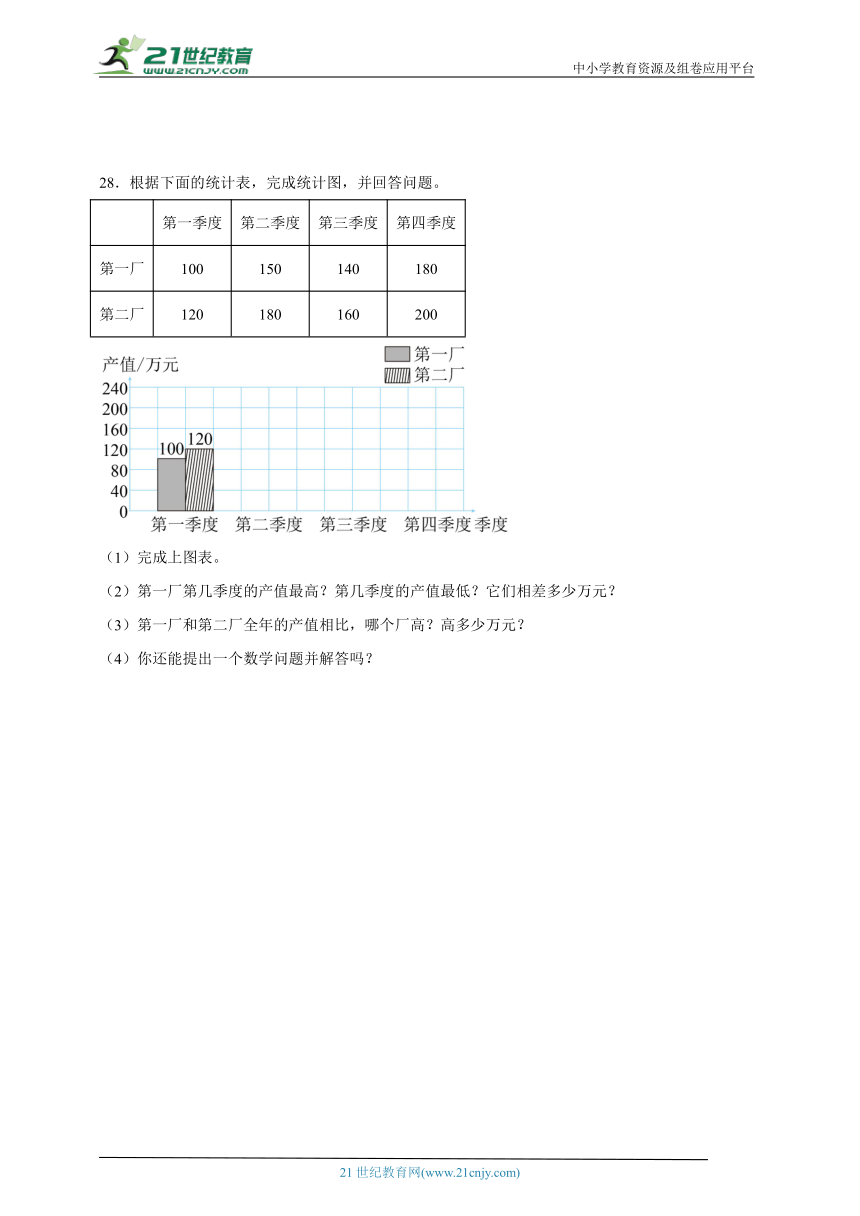
28.根据下面的统计表,完成统计图,并回答问题。
第一季度 第二季度 第三季度 第四季度
第一厂 100 150 140 180
第二厂 120 180 160 200
(1)完成上图表。
(2)第一厂第几季度的产值最高?第几季度的产值最低?它们相差多少万元?
(3)第一厂和第二厂全年的产值相比,哪个厂高?高多少万元?
(4)你还能提出一个数学问题并解答吗?
参考答案:
1.B
【分析】根据生活经验以及对容积单位、体积单位和数据大小的认识,结合实际情况选择合适的单位即可。
【详解】一台冰箱的容积约是150L。
故答案为:B
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
2.D
【分析】按照分数加减乘除计算方法分别计算出各选项的值,再比较即可。
【详解】A.9+=9.9
B.9-=8.1
C.9×=8.1
D.9=10
10>9.9>8.1
所以计算结果最大的是9。
故答案为:D
【点睛】熟练掌握分数的加减乘除的计算方法是解题的关键。
3.C
【分析】通过观察图形可知,把这个长方体锯成3个完全相同的正方体,锯了两次,3个正方体的表面积比原来长方体的表面积增加了4个切面的面积,根据正方形的面积=边长×边长,把数据代入公式解答。
【详解】5×5×4
=25×4
=100()
故答案为:C
【点睛】此题考查的目的是理解掌握正方体、长方体表面积的意义及应用,关键是知道长方体切成若干个相同的正方体后,切的次数比切成的正方体的个数少1,表面积增加数=切的次数×2。
4.B
【分析】根据正方体展开图的特征,属于“1—3—2”型,折叠成正方体后,“中”与“栗”相对,“国”与“乡”相对,“板”与“之”相对;据此解答即可。
【详解】由分析得:原正方体中,与“中”字所在的面相对的面上的字是“栗”。
故答案为:B
【点睛】此题考查了正方体展开图知识,关键是明白折成正方体后哪些面相对。
5.A
【分析】根据平均数会受到极端数据的影响,也就是平均数会受到偏大、偏小数据的影响,据此解答即可。
【详解】一位年龄45岁的老师加入游戏,老师的年龄偏大,所以对做游戏人的平均年龄影响最大。
故答案为:A
【点睛】此题考查的目的是理解平均数的意义,掌握求平均数的方法及应用。
6.C
【分析】把本月生产计划产量看作单位“1”,把实际生产时上半月和下半月完成计划的分率相加,再与单位“1”比较即可。
【详解】+=
-1=
所以本月实际产量超过计划的。
故答案为:C
【点睛】本题考查了学生解决简单的分数加法与减法的应用题的能力。
7.;
【分析】每天用该桶油的,求7天用了这桶油的几分之几,即用7×即可;将该桶油的总量看作单位“1”,用1减去7天用的油,即为剩下的。
【详解】由分析可得:
7天用的油分率:
7×=
剩下:
1-=
综上所述:妙妙家买来一桶食用油,每天做菜约用这桶油的,7天大约用了这桶油的,还剩。
【点睛】本题考查了分数乘法和分数减法的运用,求几个几分之几是多少,用乘法,求用剩下的,用减法。
8.27
【分析】把合唱团人数看作单位“1”,则参加舞蹈队人数的是合唱团人数的,其对应具体数值是18人,根据分数除法的意义,用已知的具体数值除以其对应的分率即可求出单位“1”,即合唱团人数。
【详解】由分析可得:
18÷
=18×
=27(人)
综上所述:民二小学成立了合唱团和舞蹈队。其中参加舞蹈队的有18人,是合唱团人数的,参加合唱团的有27人。
【点睛】本题是分数除法应用题,已知一个数的具体数值和其对应的分率,求单位“1”用除法。
9. 40 4
【分析】根据乘法的意义,求5个相加的和,用乘法计算;1时=60分,求一个数的几分之几是多少,用乘法计算,据此求1时的是多少分,用60乘即可解答;已知一个数的几分之几是多少,求这个数,用除法计算,据此用除以即可求出未知米数。
【详解】×5=,则5个相加的和是;
1时=60分,60×=40(分),则1时的是40分;
÷=×=4(米),则4米的是米。
【点睛】掌握分数乘法和分数除法的意义是解题的关键。
10. > = >
【分析】一个数(0除外)除以小于1的数,商大于这个数;据此判断;
根据分数除法的计算法则可知:除以一个不为零的数等于乘这个数的倒数;据此判断;
不能直接判断的先计算再比较。
【详解】<1,因此>;
=
=,由此可得由此可得=;
=1
=
=
1>
因此
>
【点睛】本题考查了分数加减、乘除的计算方法、分数的大小比较方法。
11. 150 125
【分析】根据正方体的表面积=棱长×棱长×6 ,体积=棱长×棱长×棱长,将相关数据代入公式即可求解。
【详解】一个正方体的棱长是5dm,它的表面积是:5×5×6=150(),体积:5×5×5=125()。
【点睛】此题主要考查正方体表面积和体积的计算,牢记公式、认真计算即可。
12. 9 17
【分析】可以设跳棋有x副,那么象棋就有(26-x)副,由于象棋2人下一副,跳棋6人下一副,那么下跳棋的人数+下象棋的人数=总人数,据此即可列方程,再根据等式的性质解方程即可。
【详解】解:设跳棋有x副,则象棋有(26-x)副。
6x+2(26-x)=120
6x+2×26-2x=120
4x+52=120
4x+52-52=120-52
4x=68
4x÷4=68÷4
x=17
26-17=9(副)
所以有9副象棋,17副跳棋。
【点睛】此题属于含有两个未知数的题目,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子表示,然后列方程解答。
13.90立方厘米/90cm3
【分析】根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】6×5×3
=30×3
=90(立方厘米)
一个长方体的长、宽、高分别是6厘米、5厘米和3厘米,它的体积是90立方厘米。
【点睛】熟练掌握长方体体积公式是解答本题的关键。
14./2
【分析】乘积是1的两个数叫做互为倒数。求分数的倒数,把分子和分母调换位置即可。根据题意,和A互为倒数,和B互为倒数,求出A和B的值,再把它们相加即可解答。
【详解】和A互为倒数,则A是;和B互为倒数,则B是。
+=,则A+B=
【点睛】根据求分数的倒数的方法,求出A和B的值是解题的关键。
15.√
【分析】根据平均数的意义可知,一组数据的总和除以这组数据个数所得的商,就是这组数据的平均数。平均数代表的是一组数据的平均水平,在一组数据中,有的数据有可能会大于平均数,有的数据可能会小于平均数,有的数据可能等于,平均数大于一组数据中最小值,且小于这组数据中最大值。
【详解】由分析可得:
一组数据中,任何一个数据发生变化,这组数据的总和就会发生变化,但这组数据个数没有发生变化,所以总和除以这组数据个数的商会发生变化,因此任何一个数有变化,平均数都会有反映。
故答案为:√
【点睛】本题主要考查了平均数的应用,解题时需要注意平均数与每个数据都有关。
16.√
【分析】八折就是现价是原价的十分之八,把原价看作单位“1”,它的对应的是240元,求单位“1”,用240÷解答。
【详解】八折就是现价是原价的。
240÷
=240×
=300(元)
一双运动鞋打八折销售是240元,求这双运动鞋的原价。列式为240÷。
原题干说法正确。
故答案为:√
【点睛】本题考查折扣问题,打几折就是现价是原价的十分之几。
17.×
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【详解】根据位置的相对性可知:若学校在少年宫北偏西30°方向上,则少年宫在学校南偏东30°方向上。原说法错误。
故答案为:×
【点睛】本题主要考查位置的相对性,解题时注意南偏东30°还可以表述为东偏南60°。
18.×
【分析】根据平面图中上北、下南、左西、右东的方向及图中给的角度及距离,描述出物体的位置即可。
【详解】如图,以服务中心为观测点,喷泉的位置是东偏北,距离服务中心150m。
原题说法错误。
故答案为:×
【点睛】本题主要考查根据方向、角度、距离确定物体的位置。
19.×
【分析】由于不知道这两根绳子的具体长度,所以无法确定哪根剩下部分长。分以下三种情况:
①如果两根绳子同长1米,则第一根用去的长正好是1×=米,两根用去的同样长,则剩下的同样长;
②如果两根绳子长大于1米,则第一根用去的大于米,第一根用去的长,则剩下的比第二根短;
③如果两根绳子小于1米,则第一根用去的小于米,第一根用去的短,则剩下的比第二根剩下长。
【详解】根据分析可知,两根一样长的绳子,第一根截去全长的,第二根截去米,两根剩下的绳子无法比较。
原题干说法错误。
故答案为:×
【点睛】成本题要注意题目中两个的不同意义,第一个表示占全长的分率,第二个表示具体长度。
20.;;;
7;;;
【详解】略
21.;7;;2
【分析】(1)按照运算顺序,先算加法,再算减法;
(2)利用减法的性质进行简算;
(3)利用加法运算律进行简算;
(4)利用加法运算律进行简算。
【详解】(1)
=1-
=
(2)
=8-
=8-1
=7
(3)
=
=1+
=
(4)
=
=1+1
=2
22.;
【分析】(1)先计算方程的左边,把方程化为,然后根据等式的性质,在方程的两边同时除以即可;
(2)根据等式的性质,在方程的两边同时乘即可。
【详解】
解:
解:
23.;
【分析】这题的图形是正方体,但是并不完整,被去掉了一个长方体。原本正方体有6个面,这6个面的面积和就是该正方体的表面积。现在通过观察可以发现,虽然去掉了一个长方体,但是根据长方体的特征,相对的面面积相对等,该正方体的表面积并没有发生变化。而该正方体的体积,用原来完整的正方体的体积减去被去掉的长方体的体积即可。
【详解】正方体表面积:
12×12×6
=144×6
=864(cm2)
完整正方体的体积:
12×12×12
=144×12
=1728(cm3)
去掉的长方体的体积:
6×6×8
=36×8
=288(cm3)
所求图形的体积:
1728-288=1440(cm3)
24.3时
【分析】设x时后两车相遇,甲车速度是70千米/时,x时行驶70x千米;乙车的速度是80千米/时,x时行驶80x千米,甲车行驶的距离+乙车行驶的距离=甲、乙两地的距离,列方程:70x+80x=450,解方程,即可解答。
【详解】解:设x时后两车相遇。
70x+80x=450
150x=450
x=450÷150
x=3
答:3时后两车相遇。
【点睛】根据方程的实际应用,利用速度、时间和距离三者的关系,设出未知数,找出相关的量,列方程,解方程。
25.220人
【分析】由题可知:六年级女生人数+六年级男生人数=全年级总人数,设全年级共有x人,根据六年级女生的人数比全年级人数的少5人,则六年级女生有()人,同理可知,六年级男生有()人,据此根据等量关系列方程解答即可。
【详解】解:设全年级共有x人。
x=220
答:全年级共有220人。
【点睛】本题主要考查分数除法的应用,列方程解决问题的关键是根据已知条件找出等量关系。
26.300公顷
【分析】根据题意,张叔叔的农场共1200公顷,其中果园的面积占了农场的,用1200乘,即可求得果园的面积;又因为种植香蕉的面积占了果园的,再用果园的面积乘即可求得种植香蕉的面积。
【详解】由分析得:
1200××
=1200×
=300(公顷)
答:张叔叔的农场种植香蕉的面积是300公顷。
【点睛】本题主要考查分数连乘的实际应用,解题的关键是找准单位“1”。
27.1.5米
【分析】根据题意,A处下降的体积=B处上升的体积,利用长方体的体积公式V=Sh,设A处下降了x米,则B处上升了(4-x)米;据此根据等量关系列方程解答。
【详解】解:设A处下降了x米,则B处上升了(4-x)米。
25x=15×(4-x)
25x=60-15x
25x+15x=60
40x=60
x=60÷40
x=1.5
答:A处下降了1.5米。
【点睛】本题主要考查学生对长方体体积公式的掌握与灵活运用,明确A处下降的高度加上B处上升的高度等于4米是解题的关键。
28.(1)见详解
(2)第四季度;第一季度;80万元
(3)第二厂;90万元
(4)第一厂和第二厂第一季度总产值是多少万元?220万元
【分析】(1)根据数据画出长短不同的直条,并注明数据,注意第一厂和第二厂图例颜色即可。
(2)观察复式条形统计图,直条越高表示产值越高,直条越矮表示产值越低,求差即可。
(3)分别将第一厂和第二厂四个季度产值相加,求出第一厂和第二厂全年的产值,比较并求差即可。
(4)答案不唯一,如第一厂和第二厂第一季度总产值是多少万元?将第一厂和第二厂第一季度产值相加即可。
【详解】
(1)
(2)180-100=80(万元)
答:第一厂第四季度的产值最高,第一季度的产值最低,它们相差80万元。
(3)100+150+140+180=570(万元)
120+180+160+200=660(万元)
570<660
660-570=90(万元)
答:第二厂产值高,高90万元。
(4)第一厂和第二厂第一季度总产值是多少万元?
100+120=220(万元)
答:第一厂和第二厂第一季度总产值是220万元。
(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟测试卷(试题)2023-2024学年数学五年级下册北师大版
一、选择题
1.一台冰箱的容积约是150( )。
A.cm3 B.L C.mL D.m3
2.下列算式中,计算结果最大的是( )。
A. B. C. D.
3.如图,把一段长方体的木料锯成3个完全相同的小正方体后,3个小正方体的表面积之和比原长方体的表面积增加了( )。
A.25 B.50 C.100 D.200
4.镇安大板栗以个大色润、甜脆可口、颗粒饱满、营养丰富、品质独特而闻名全国,被誉为“中国板栗之乡”。如图是一个正方体的平面展开图,则原正方体中,与“中”字所在的面相对的面上的字是( )。
A.板 B.栗 C.之 D.乡
5.操场上有8个小朋友在做游戏,他们的年龄分别是7岁、7岁、7岁、8岁、8岁、8岁、9岁、9岁,笑笑算了一下这些小朋友的平均年龄为7.875岁。下面( )种情况对做游戏人的平均年龄影响最大。
A.一位年龄45岁的老师加入游戏 B.5位年龄为7岁的小朋友加入游戏
C.8位年龄为8岁的小朋友加入游戏 D.两位9岁的小朋友离开游戏队伍
6.工厂计划本月生产一批零件。实际生产时发现上半月完成计划的,下半月完成计划的,下面说法正确的是( )。
A.本月生产计划没有完成 B.本月实际产量是计划的
C.本月实际产量超过计划的 D.本月产量超过计划的主要原因是上半月生产效率高
二、填空题
7.妙妙家买来一桶食用油,每天做菜约用这桶油的,7天大约用了这桶油的,还剩( )。
8.民二小学成立了合唱团和舞蹈队。其中参加舞蹈队的有18人,是合唱团人数的,参加合唱团的有( )人。
9.5个相加的和是( ),1时的是( )分,( )米的是米。
10.在( )里填上“>”“<”或“=”。
( ) ( ) ( )
11.一个正方体的棱长是5dm,它的表面积是( ),体积是( )。
12.为有效落实国家“双减”政策,加强学校特色建设,丰富学生校园文化生活,光明小学开展了丰富多彩的社团活动。其中棋艺社团有象棋、跳棋共26副,恰好可供120个学生同时进行活动,象棋2人下一副棋,跳棋6人下一副,有( )副象棋和( )副跳棋。
13.一个长方体的长、宽、高分别是6厘米、5厘米和3厘米,它的体积是( ) 。
14.如果,那么A+B=( )。
三、判断题
15.平均数能够代表一组数据的平均水平,任何一个数有变化,平均数都有反应。( )
16.一双运动鞋打八折销售是240元,求这双运动鞋的原价。列式为。( )
17.若学校在少年宫北偏西30°方向上,则少年宫在学校南偏东60°方向上。( )
18.如图,以服务中心为观测点,喷泉的位置是北偏东,距离服务中心150m。( )
19.两根一样长的绳子,第一根截去全长的,第二根截去米,两根剩下的绳子一样长。( )
四、计算题
20.直接写出得数。
21.用你喜欢的方法计算。
22.求未知数x。
23.计算下面图形的表面积和体积。
五、解答题
24.甲、乙两辆汽车从相距450千米的两地同时出发,相向而行。甲车速度是70千米/时,乙车的速度是80千米/时,几时后两车相遇?
25.阳光小学六年级女生的人数比全年级人数的少5人,男生人数比全年级人数的多16人,求全年级共有多少人?
26.张叔叔的农场共1200公顷,其中果园的面积占了农场的,种植香蕉的面积占了果园的,张叔叔的农场种植香蕉的面积是多少公顷?
27.一堆黄土如图所示,已知A的面积是25平方米,B的面积是15平方米,A处比B处高4米,现在把A处的土推向B处,使A、B两处同样高。A处下降了多少米?
28.根据下面的统计表,完成统计图,并回答问题。
第一季度 第二季度 第三季度 第四季度
第一厂 100 150 140 180
第二厂 120 180 160 200
(1)完成上图表。
(2)第一厂第几季度的产值最高?第几季度的产值最低?它们相差多少万元?
(3)第一厂和第二厂全年的产值相比,哪个厂高?高多少万元?
(4)你还能提出一个数学问题并解答吗?
参考答案:
1.B
【分析】根据生活经验以及对容积单位、体积单位和数据大小的认识,结合实际情况选择合适的单位即可。
【详解】一台冰箱的容积约是150L。
故答案为:B
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
2.D
【分析】按照分数加减乘除计算方法分别计算出各选项的值,再比较即可。
【详解】A.9+=9.9
B.9-=8.1
C.9×=8.1
D.9=10
10>9.9>8.1
所以计算结果最大的是9。
故答案为:D
【点睛】熟练掌握分数的加减乘除的计算方法是解题的关键。
3.C
【分析】通过观察图形可知,把这个长方体锯成3个完全相同的正方体,锯了两次,3个正方体的表面积比原来长方体的表面积增加了4个切面的面积,根据正方形的面积=边长×边长,把数据代入公式解答。
【详解】5×5×4
=25×4
=100()
故答案为:C
【点睛】此题考查的目的是理解掌握正方体、长方体表面积的意义及应用,关键是知道长方体切成若干个相同的正方体后,切的次数比切成的正方体的个数少1,表面积增加数=切的次数×2。
4.B
【分析】根据正方体展开图的特征,属于“1—3—2”型,折叠成正方体后,“中”与“栗”相对,“国”与“乡”相对,“板”与“之”相对;据此解答即可。
【详解】由分析得:原正方体中,与“中”字所在的面相对的面上的字是“栗”。
故答案为:B
【点睛】此题考查了正方体展开图知识,关键是明白折成正方体后哪些面相对。
5.A
【分析】根据平均数会受到极端数据的影响,也就是平均数会受到偏大、偏小数据的影响,据此解答即可。
【详解】一位年龄45岁的老师加入游戏,老师的年龄偏大,所以对做游戏人的平均年龄影响最大。
故答案为:A
【点睛】此题考查的目的是理解平均数的意义,掌握求平均数的方法及应用。
6.C
【分析】把本月生产计划产量看作单位“1”,把实际生产时上半月和下半月完成计划的分率相加,再与单位“1”比较即可。
【详解】+=
-1=
所以本月实际产量超过计划的。
故答案为:C
【点睛】本题考查了学生解决简单的分数加法与减法的应用题的能力。
7.;
【分析】每天用该桶油的,求7天用了这桶油的几分之几,即用7×即可;将该桶油的总量看作单位“1”,用1减去7天用的油,即为剩下的。
【详解】由分析可得:
7天用的油分率:
7×=
剩下:
1-=
综上所述:妙妙家买来一桶食用油,每天做菜约用这桶油的,7天大约用了这桶油的,还剩。
【点睛】本题考查了分数乘法和分数减法的运用,求几个几分之几是多少,用乘法,求用剩下的,用减法。
8.27
【分析】把合唱团人数看作单位“1”,则参加舞蹈队人数的是合唱团人数的,其对应具体数值是18人,根据分数除法的意义,用已知的具体数值除以其对应的分率即可求出单位“1”,即合唱团人数。
【详解】由分析可得:
18÷
=18×
=27(人)
综上所述:民二小学成立了合唱团和舞蹈队。其中参加舞蹈队的有18人,是合唱团人数的,参加合唱团的有27人。
【点睛】本题是分数除法应用题,已知一个数的具体数值和其对应的分率,求单位“1”用除法。
9. 40 4
【分析】根据乘法的意义,求5个相加的和,用乘法计算;1时=60分,求一个数的几分之几是多少,用乘法计算,据此求1时的是多少分,用60乘即可解答;已知一个数的几分之几是多少,求这个数,用除法计算,据此用除以即可求出未知米数。
【详解】×5=,则5个相加的和是;
1时=60分,60×=40(分),则1时的是40分;
÷=×=4(米),则4米的是米。
【点睛】掌握分数乘法和分数除法的意义是解题的关键。
10. > = >
【分析】一个数(0除外)除以小于1的数,商大于这个数;据此判断;
根据分数除法的计算法则可知:除以一个不为零的数等于乘这个数的倒数;据此判断;
不能直接判断的先计算再比较。
【详解】<1,因此>;
=
=,由此可得由此可得=;
=1
=
=
1>
因此
>
【点睛】本题考查了分数加减、乘除的计算方法、分数的大小比较方法。
11. 150 125
【分析】根据正方体的表面积=棱长×棱长×6 ,体积=棱长×棱长×棱长,将相关数据代入公式即可求解。
【详解】一个正方体的棱长是5dm,它的表面积是:5×5×6=150(),体积:5×5×5=125()。
【点睛】此题主要考查正方体表面积和体积的计算,牢记公式、认真计算即可。
12. 9 17
【分析】可以设跳棋有x副,那么象棋就有(26-x)副,由于象棋2人下一副,跳棋6人下一副,那么下跳棋的人数+下象棋的人数=总人数,据此即可列方程,再根据等式的性质解方程即可。
【详解】解:设跳棋有x副,则象棋有(26-x)副。
6x+2(26-x)=120
6x+2×26-2x=120
4x+52=120
4x+52-52=120-52
4x=68
4x÷4=68÷4
x=17
26-17=9(副)
所以有9副象棋,17副跳棋。
【点睛】此题属于含有两个未知数的题目,这类题用方程解答比较容易,关键是找准数量间的相等关系,设一个未知数为x,另一个未知数用含x的式子表示,然后列方程解答。
13.90立方厘米/90cm3
【分析】根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】6×5×3
=30×3
=90(立方厘米)
一个长方体的长、宽、高分别是6厘米、5厘米和3厘米,它的体积是90立方厘米。
【点睛】熟练掌握长方体体积公式是解答本题的关键。
14./2
【分析】乘积是1的两个数叫做互为倒数。求分数的倒数,把分子和分母调换位置即可。根据题意,和A互为倒数,和B互为倒数,求出A和B的值,再把它们相加即可解答。
【详解】和A互为倒数,则A是;和B互为倒数,则B是。
+=,则A+B=
【点睛】根据求分数的倒数的方法,求出A和B的值是解题的关键。
15.√
【分析】根据平均数的意义可知,一组数据的总和除以这组数据个数所得的商,就是这组数据的平均数。平均数代表的是一组数据的平均水平,在一组数据中,有的数据有可能会大于平均数,有的数据可能会小于平均数,有的数据可能等于,平均数大于一组数据中最小值,且小于这组数据中最大值。
【详解】由分析可得:
一组数据中,任何一个数据发生变化,这组数据的总和就会发生变化,但这组数据个数没有发生变化,所以总和除以这组数据个数的商会发生变化,因此任何一个数有变化,平均数都会有反映。
故答案为:√
【点睛】本题主要考查了平均数的应用,解题时需要注意平均数与每个数据都有关。
16.√
【分析】八折就是现价是原价的十分之八,把原价看作单位“1”,它的对应的是240元,求单位“1”,用240÷解答。
【详解】八折就是现价是原价的。
240÷
=240×
=300(元)
一双运动鞋打八折销售是240元,求这双运动鞋的原价。列式为240÷。
原题干说法正确。
故答案为:√
【点睛】本题考查折扣问题,打几折就是现价是原价的十分之几。
17.×
【分析】根据位置的相对性可知,它们的方向相反,角度相等,距离相等,据此解答。
【详解】根据位置的相对性可知:若学校在少年宫北偏西30°方向上,则少年宫在学校南偏东30°方向上。原说法错误。
故答案为:×
【点睛】本题主要考查位置的相对性,解题时注意南偏东30°还可以表述为东偏南60°。
18.×
【分析】根据平面图中上北、下南、左西、右东的方向及图中给的角度及距离,描述出物体的位置即可。
【详解】如图,以服务中心为观测点,喷泉的位置是东偏北,距离服务中心150m。
原题说法错误。
故答案为:×
【点睛】本题主要考查根据方向、角度、距离确定物体的位置。
19.×
【分析】由于不知道这两根绳子的具体长度,所以无法确定哪根剩下部分长。分以下三种情况:
①如果两根绳子同长1米,则第一根用去的长正好是1×=米,两根用去的同样长,则剩下的同样长;
②如果两根绳子长大于1米,则第一根用去的大于米,第一根用去的长,则剩下的比第二根短;
③如果两根绳子小于1米,则第一根用去的小于米,第一根用去的短,则剩下的比第二根剩下长。
【详解】根据分析可知,两根一样长的绳子,第一根截去全长的,第二根截去米,两根剩下的绳子无法比较。
原题干说法错误。
故答案为:×
【点睛】成本题要注意题目中两个的不同意义,第一个表示占全长的分率,第二个表示具体长度。
20.;;;
7;;;
【详解】略
21.;7;;2
【分析】(1)按照运算顺序,先算加法,再算减法;
(2)利用减法的性质进行简算;
(3)利用加法运算律进行简算;
(4)利用加法运算律进行简算。
【详解】(1)
=1-
=
(2)
=8-
=8-1
=7
(3)
=
=1+
=
(4)
=
=1+1
=2
22.;
【分析】(1)先计算方程的左边,把方程化为,然后根据等式的性质,在方程的两边同时除以即可;
(2)根据等式的性质,在方程的两边同时乘即可。
【详解】
解:
解:
23.;
【分析】这题的图形是正方体,但是并不完整,被去掉了一个长方体。原本正方体有6个面,这6个面的面积和就是该正方体的表面积。现在通过观察可以发现,虽然去掉了一个长方体,但是根据长方体的特征,相对的面面积相对等,该正方体的表面积并没有发生变化。而该正方体的体积,用原来完整的正方体的体积减去被去掉的长方体的体积即可。
【详解】正方体表面积:
12×12×6
=144×6
=864(cm2)
完整正方体的体积:
12×12×12
=144×12
=1728(cm3)
去掉的长方体的体积:
6×6×8
=36×8
=288(cm3)
所求图形的体积:
1728-288=1440(cm3)
24.3时
【分析】设x时后两车相遇,甲车速度是70千米/时,x时行驶70x千米;乙车的速度是80千米/时,x时行驶80x千米,甲车行驶的距离+乙车行驶的距离=甲、乙两地的距离,列方程:70x+80x=450,解方程,即可解答。
【详解】解:设x时后两车相遇。
70x+80x=450
150x=450
x=450÷150
x=3
答:3时后两车相遇。
【点睛】根据方程的实际应用,利用速度、时间和距离三者的关系,设出未知数,找出相关的量,列方程,解方程。
25.220人
【分析】由题可知:六年级女生人数+六年级男生人数=全年级总人数,设全年级共有x人,根据六年级女生的人数比全年级人数的少5人,则六年级女生有()人,同理可知,六年级男生有()人,据此根据等量关系列方程解答即可。
【详解】解:设全年级共有x人。
x=220
答:全年级共有220人。
【点睛】本题主要考查分数除法的应用,列方程解决问题的关键是根据已知条件找出等量关系。
26.300公顷
【分析】根据题意,张叔叔的农场共1200公顷,其中果园的面积占了农场的,用1200乘,即可求得果园的面积;又因为种植香蕉的面积占了果园的,再用果园的面积乘即可求得种植香蕉的面积。
【详解】由分析得:
1200××
=1200×
=300(公顷)
答:张叔叔的农场种植香蕉的面积是300公顷。
【点睛】本题主要考查分数连乘的实际应用,解题的关键是找准单位“1”。
27.1.5米
【分析】根据题意,A处下降的体积=B处上升的体积,利用长方体的体积公式V=Sh,设A处下降了x米,则B处上升了(4-x)米;据此根据等量关系列方程解答。
【详解】解:设A处下降了x米,则B处上升了(4-x)米。
25x=15×(4-x)
25x=60-15x
25x+15x=60
40x=60
x=60÷40
x=1.5
答:A处下降了1.5米。
【点睛】本题主要考查学生对长方体体积公式的掌握与灵活运用,明确A处下降的高度加上B处上升的高度等于4米是解题的关键。
28.(1)见详解
(2)第四季度;第一季度;80万元
(3)第二厂;90万元
(4)第一厂和第二厂第一季度总产值是多少万元?220万元
【分析】(1)根据数据画出长短不同的直条,并注明数据,注意第一厂和第二厂图例颜色即可。
(2)观察复式条形统计图,直条越高表示产值越高,直条越矮表示产值越低,求差即可。
(3)分别将第一厂和第二厂四个季度产值相加,求出第一厂和第二厂全年的产值,比较并求差即可。
(4)答案不唯一,如第一厂和第二厂第一季度总产值是多少万元?将第一厂和第二厂第一季度产值相加即可。
【详解】
(1)
(2)180-100=80(万元)
答:第一厂第四季度的产值最高,第一季度的产值最低,它们相差80万元。
(3)100+150+140+180=570(万元)
120+180+160+200=660(万元)
570<660
660-570=90(万元)
答:第二厂产值高,高90万元。
(4)第一厂和第二厂第一季度总产值是多少万元?
100+120=220(万元)
答:第一厂和第二厂第一季度总产值是220万元。
(答案不唯一)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
