湘教版初中数学八年级上册1.3整数指数幂 课件(共34张PPT)
文档属性
| 名称 | 湘教版初中数学八年级上册1.3整数指数幂 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-05 18:31:46 | ||
图片预览





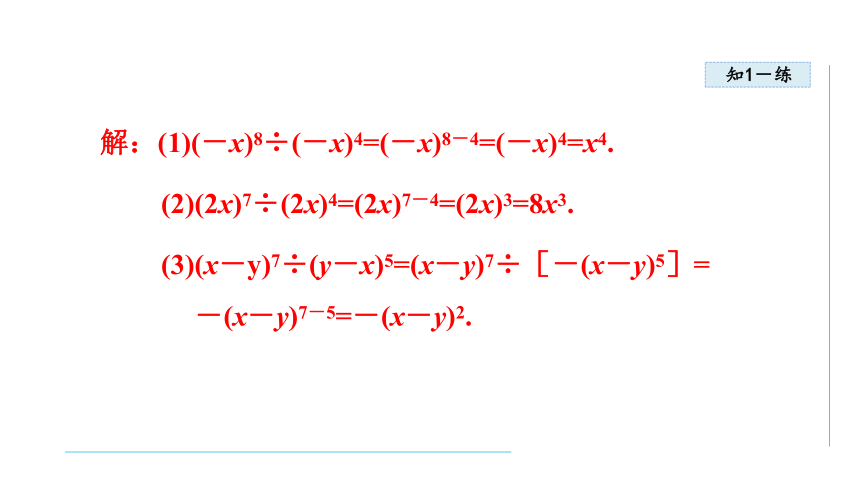




文档简介
(共34张PPT)
1.3 整数指数幂
第1章 分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
同底数幂的除法
零次幂和负整数指数幂
科学记数法
整数指数幂的运算法则
知识点
同底数幂的除法
知1-讲
感悟新知
1
1.同底数幂相除的运算法则:
同底数幂相除,底数不变,指数相减.
即: =am-n(a≠0,m,n都是正整数,且m>n).
知1-讲
感悟新知
2. 法则的拓展运用:
(1)法则的推广:适用于三个及三个以上的同底数幂相除,即am÷an÷ap=am-n - p(a ≠ 0,m,n,p 是正整数,且m>n+p);
(2)同底数幂相除的运算法则既可以正用,也可以逆用,逆用时am-n= (a ≠ 0,m,n 是正整数,且m>n).
知1-讲
感悟新知
特别解读
1. 运用法则的关键有两点:一是底数相同,二是除法运算,二者缺一不可.
2.底数a可以是单项式,也可以是多项式,但底数a不能为0.
3.同底数幂相除,底数不变,指数相减,而不是相除.
知1-练
感悟新知
例 1
计算:
(1)(-x)8÷(-x)4;
(2)(2x)7÷(2x)4;
(3)(x-y)7÷(y-x)5.
解题秘方:同底数幂相除,底数不变,指数相减.
知1-练
感悟新知
解:(1)(-x)8÷(-x)4=(-x)8-4=(-x)4=x4.
(2)(2x)7÷(2x)4=(2x)7-4=(2x)3=8x3.
(3)(x-y)7÷(y-x)5=(x-y)7÷[-(x-y)5]=
-(x-y)7-5=-(x-y)2.
知1-练
感悟新知
已知xm=9,xn=27,求x3m-2n 的值.
例2
解题秘方:同底数幂相除,底数不变,指数相减.
方法点拨:逆向运用同底数幂相乘除和幂的乘方的运算法则求值的方法:当幂的指数是含有字母的加法时,通常转化为同底数幂的乘法;当幂的指数是含有字母的减法时,通常转化为同底数幂的除法;当幂的指数是含有字母的乘法时,通常转化为幂的乘方,然后整体代入求值.
知1-练
感悟新知
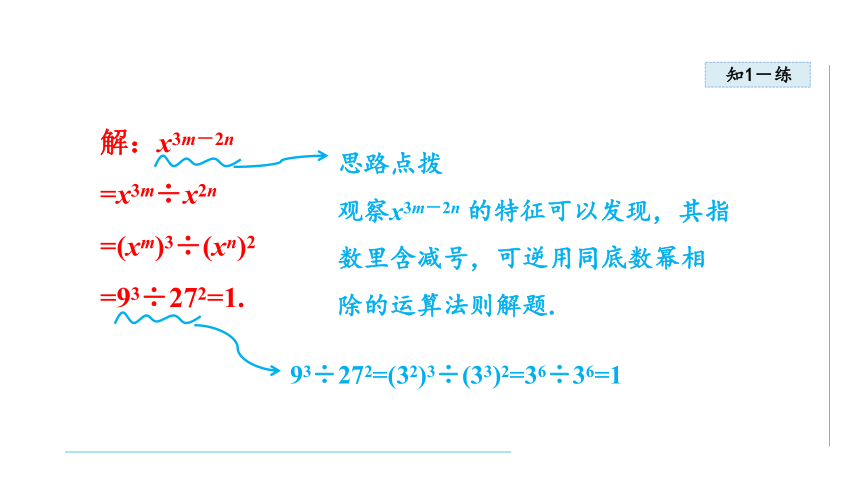
解:x3m-2n
=x3m÷x2n
=(xm)3÷(xn)2
=93÷272=1.
思路点拨
观察x3m-2n 的特征可以发现,其指数里含减号,可逆用同底数幂相除的运算法则解题.
93÷272=(32)3÷(33)2=36÷36=1
知识点
零次幂和负整数指数幂
知2-讲
感悟新知
2
1. 零次幂:
(1)任何不等于零的数的零次幂都等于1.
(2)零次幂要把握三点:①底数不为零;②指数为零;③结果是1.
知2-讲
感悟新知
2. 负整数指数幂:
(1)任何不等于零的数的-n(n 为正整数)次幂,等于这个数的n 次幂的倒数. 即a-n= (a ≠ 0,n 是正整数).
(2)由于 ,因此a-n= (a ≠ 0,n 是正整数)
知2-讲
感悟新知
特别提醒
1. 在a0=1 中规定a ≠0,原因是00 无意义.
2. 在a0=1 中,a 可以是非零的有理数,也可以是多项式或非零的单项式.
3. =an(a ≠ 0,n为正整数)仍然成立.
感悟新知
知2-练
计算:
例 3
解题秘方:紧扣零次幂和负整数指数幂的运算法则进行计算.
知2-讲
感悟新知
解法提醒
对于底数是分数的负整数指数幂,我们可采用底倒指反法,将其转化为这个数的倒数的正整数指数幂,即
感悟新知
知2-练
答案:12
感悟新知
知2-练
把下列各式写成分式的形式:
(1)y-3; (2)3x-3y.
解题秘方:直接用负整数指数幂的运算法则求解.
例4
知2-讲
感悟新知
方法总结
在化简、计算中,结果不能含有负整数指数幂,如果出现负整数指数幂,需要化成对应的正整数指数幂来表示.
感悟新知
知2-练
知识点
科学记数法
知3-讲
感悟新知
3
1. 用科学记数法表示数:一般地,把一些绝对值较大的数表示成a×10n 的形式,其中a 的取值范围是1 ≤ |a|<10,n 是正整数;把一些绝对值较小的数表示成a×10-n 的形式,其中a 的取值范围是1 ≤ |a|<10,n 是正整数. 用这两种形式表示数的方法称为科学记数法. 用科学记数法表示绝对值较小的数时,关键是掌握公式:
知3-讲
感悟新知
2. 用科学记数法表示绝对值较小的数的一般步骤:
(1)确定a:a 是只有一位整数的数.
(2)确定n:确定n 的方法有两个,即① n 等于原数中左起第一个非零数前0 的个数(包括小数点前的那个0);②小数点向右移到第一个非零的数后,小数点移动了几位,n 就等于几.
(3)将原数用科学记数法表示为a×10-n( 其中1 ≤|a|<10,n 是正整数).
知3-讲
感悟新知
特别提醒
用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n前面的“- ”号.
感悟新知
知3-练
用科学记数法表示下列各数:
(1)0.000 003; (2)-0.000 020 8.
解题秘方:按照科学记数法的要求,将各数写成±a×10-n的形式,其中1 ≤ a<10,n 是正整数.
例 5
教你一招
用科学记数法表示绝对值较小的数的思路:
用科学记数法表示绝对值较小的数时,一般形式为a×10-n, 其中1 ≤ |a|<10,n 由原数左起第一个不为零的数字前面0 的个数决定.
感悟新知
知3-练
解:(1)0.000 003=3×10-6.
(2)-0.000 020 8=-2.08×10-5.
3 前面有6 个0
2 前面有5 个0
感悟新知
知3-练
将下列用科学记数法表示的数还原成原数.
(1)-7.2×10-5; (2)5.68×10-6.
解题秘方:把用科学记数法表示的绝对值较小的数还原时,指数的绝对值是几,小数点就向左移动几位.
教你一招
将用科学记数法表示的绝对值较小的数还原的思路:
把a×10-n( 其中1 ≤ |a|<10,n 是正整数)还原成原数时,只要把a 的小数点向左移动n 位即可.
例6
感悟新知
知3-练
解:(1)-7.2×10-5=-0.000 072.
(2)5.68×10-6=0.000 005 68.
感悟新知
知3-练
计算:
(1)(3×10-4)2×(2×10-6)3;
(2)(8×10-7)2÷(2×10-3)3.
解题秘方:先计算乘方,再计算乘除.
例 7
解法提醒
计算用科学记数法表示的数的运算时,乘方运算用积的乘方运算法则,乘除运算用单项式乘除运算法则,计算的结果也应该用科学记数法形式表示.
感悟新知
知3-练
解:(1)原式=9×10-8×8×10-18
=(9×8)×(10-8×10-18)
=7.2×10-25.
(2)原式=(64×10-14)÷(8×10-9)
= (64÷8)×(10-14÷10-9)
= 8×10-5.
知识点
整数指数幂的运算法则
知4-讲
感悟新知
4
运算法则 公式
幂 的 运 算 同底数幂的乘法 同底数幂相乘,底数不变,指数相加 ① am·an=am+n(a ≠ 0,m,n 都是整数)
幂的乘方 幂的乘方,底数不变,指数相乘 (am)n=amn(a ≠ 0,m,n 都是整数)
知4-讲
感悟新知
幂 的 运 算 积的乘方 积的乘方等于各因 数分别乘方的积 ②(ab)n=anbn(a ≠ 0,b ≠ 0,n是整数)
同底数幂 的除法 同底数幂相除,底 数不变,指数相减 =am·a-n=am+(-n)=am-n(a ≠ 0,m,n 都是整数)
分式的 乘方 分式乘方等于分 子、分母分别乘方 =(a·b-1)n=an·(b-1)n=
an·b-n= (a ≠ 0,b ≠ 0,n 是整数)
知4-讲
感悟新知
特别提醒
同底数幂相除的运算法则被包含在公式①中,分式的乘方的运算法则被包含在公式②中.
感悟新知
知4-练
计算:
(1)(-m2n-3)·(3m-3n-2);(2)(2a-2)3b2÷4a-8b3;
解题秘方:按照先乘方,再乘除的顺序进行计算.
例8
感悟新知
知4-练
方法点拨
1. 幂的运算法则适用于任何整数指数幂.
2. 计算底数是分式的幂的运算时,先将分式形式的幂改写,分子的指数不变,分母的指数改为相反数,然后再按幂的运算法则计算.
3. 运算的结果有负指数的,要改写成分式的形式.
感悟新知
知4-练
解:(1)原式=-1×3×m2+(-3)×n-3-2=-3m-1n-5=-
(2)原式=8a-6b2÷4a-8b3=2a2b-1=
(3)原式=x-4y2·y-6x3÷x4y-4=x-4y2·x3y-6·x-4y4=
x-5y0=
课堂小结
整数指数幂
整数指数幂
同底数幂的除法
正整数指数幂
负整数指数幂
零次幂
科学计数法
结果
1.3 整数指数幂
第1章 分式
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
同底数幂的除法
零次幂和负整数指数幂
科学记数法
整数指数幂的运算法则
知识点
同底数幂的除法
知1-讲
感悟新知
1
1.同底数幂相除的运算法则:
同底数幂相除,底数不变,指数相减.
即: =am-n(a≠0,m,n都是正整数,且m>n).
知1-讲
感悟新知
2. 法则的拓展运用:
(1)法则的推广:适用于三个及三个以上的同底数幂相除,即am÷an÷ap=am-n - p(a ≠ 0,m,n,p 是正整数,且m>n+p);
(2)同底数幂相除的运算法则既可以正用,也可以逆用,逆用时am-n= (a ≠ 0,m,n 是正整数,且m>n).
知1-讲
感悟新知
特别解读
1. 运用法则的关键有两点:一是底数相同,二是除法运算,二者缺一不可.
2.底数a可以是单项式,也可以是多项式,但底数a不能为0.
3.同底数幂相除,底数不变,指数相减,而不是相除.
知1-练
感悟新知
例 1
计算:
(1)(-x)8÷(-x)4;
(2)(2x)7÷(2x)4;
(3)(x-y)7÷(y-x)5.
解题秘方:同底数幂相除,底数不变,指数相减.
知1-练
感悟新知
解:(1)(-x)8÷(-x)4=(-x)8-4=(-x)4=x4.
(2)(2x)7÷(2x)4=(2x)7-4=(2x)3=8x3.
(3)(x-y)7÷(y-x)5=(x-y)7÷[-(x-y)5]=
-(x-y)7-5=-(x-y)2.
知1-练
感悟新知
已知xm=9,xn=27,求x3m-2n 的值.
例2
解题秘方:同底数幂相除,底数不变,指数相减.
方法点拨:逆向运用同底数幂相乘除和幂的乘方的运算法则求值的方法:当幂的指数是含有字母的加法时,通常转化为同底数幂的乘法;当幂的指数是含有字母的减法时,通常转化为同底数幂的除法;当幂的指数是含有字母的乘法时,通常转化为幂的乘方,然后整体代入求值.
知1-练
感悟新知
解:x3m-2n
=x3m÷x2n
=(xm)3÷(xn)2
=93÷272=1.
思路点拨
观察x3m-2n 的特征可以发现,其指数里含减号,可逆用同底数幂相除的运算法则解题.
93÷272=(32)3÷(33)2=36÷36=1
知识点
零次幂和负整数指数幂
知2-讲
感悟新知
2
1. 零次幂:
(1)任何不等于零的数的零次幂都等于1.
(2)零次幂要把握三点:①底数不为零;②指数为零;③结果是1.
知2-讲
感悟新知
2. 负整数指数幂:
(1)任何不等于零的数的-n(n 为正整数)次幂,等于这个数的n 次幂的倒数. 即a-n= (a ≠ 0,n 是正整数).
(2)由于 ,因此a-n= (a ≠ 0,n 是正整数)
知2-讲
感悟新知
特别提醒
1. 在a0=1 中规定a ≠0,原因是00 无意义.
2. 在a0=1 中,a 可以是非零的有理数,也可以是多项式或非零的单项式.
3. =an(a ≠ 0,n为正整数)仍然成立.
感悟新知
知2-练
计算:
例 3
解题秘方:紧扣零次幂和负整数指数幂的运算法则进行计算.
知2-讲
感悟新知
解法提醒
对于底数是分数的负整数指数幂,我们可采用底倒指反法,将其转化为这个数的倒数的正整数指数幂,即
感悟新知
知2-练
答案:12
感悟新知
知2-练
把下列各式写成分式的形式:
(1)y-3; (2)3x-3y.
解题秘方:直接用负整数指数幂的运算法则求解.
例4
知2-讲
感悟新知
方法总结
在化简、计算中,结果不能含有负整数指数幂,如果出现负整数指数幂,需要化成对应的正整数指数幂来表示.
感悟新知
知2-练
知识点
科学记数法
知3-讲
感悟新知
3
1. 用科学记数法表示数:一般地,把一些绝对值较大的数表示成a×10n 的形式,其中a 的取值范围是1 ≤ |a|<10,n 是正整数;把一些绝对值较小的数表示成a×10-n 的形式,其中a 的取值范围是1 ≤ |a|<10,n 是正整数. 用这两种形式表示数的方法称为科学记数法. 用科学记数法表示绝对值较小的数时,关键是掌握公式:
知3-讲
感悟新知
2. 用科学记数法表示绝对值较小的数的一般步骤:
(1)确定a:a 是只有一位整数的数.
(2)确定n:确定n 的方法有两个,即① n 等于原数中左起第一个非零数前0 的个数(包括小数点前的那个0);②小数点向右移到第一个非零的数后,小数点移动了几位,n 就等于几.
(3)将原数用科学记数法表示为a×10-n( 其中1 ≤|a|<10,n 是正整数).
知3-讲
感悟新知
特别提醒
用科学记数法表示绝对值小于1的数时,10的指数是负数,一定不要忘记指数n前面的“- ”号.
感悟新知
知3-练
用科学记数法表示下列各数:
(1)0.000 003; (2)-0.000 020 8.
解题秘方:按照科学记数法的要求,将各数写成±a×10-n的形式,其中1 ≤ a<10,n 是正整数.
例 5
教你一招
用科学记数法表示绝对值较小的数的思路:
用科学记数法表示绝对值较小的数时,一般形式为a×10-n, 其中1 ≤ |a|<10,n 由原数左起第一个不为零的数字前面0 的个数决定.
感悟新知
知3-练
解:(1)0.000 003=3×10-6.
(2)-0.000 020 8=-2.08×10-5.
3 前面有6 个0
2 前面有5 个0
感悟新知
知3-练
将下列用科学记数法表示的数还原成原数.
(1)-7.2×10-5; (2)5.68×10-6.
解题秘方:把用科学记数法表示的绝对值较小的数还原时,指数的绝对值是几,小数点就向左移动几位.
教你一招
将用科学记数法表示的绝对值较小的数还原的思路:
把a×10-n( 其中1 ≤ |a|<10,n 是正整数)还原成原数时,只要把a 的小数点向左移动n 位即可.
例6
感悟新知
知3-练
解:(1)-7.2×10-5=-0.000 072.
(2)5.68×10-6=0.000 005 68.
感悟新知
知3-练
计算:
(1)(3×10-4)2×(2×10-6)3;
(2)(8×10-7)2÷(2×10-3)3.
解题秘方:先计算乘方,再计算乘除.
例 7
解法提醒
计算用科学记数法表示的数的运算时,乘方运算用积的乘方运算法则,乘除运算用单项式乘除运算法则,计算的结果也应该用科学记数法形式表示.
感悟新知
知3-练
解:(1)原式=9×10-8×8×10-18
=(9×8)×(10-8×10-18)
=7.2×10-25.
(2)原式=(64×10-14)÷(8×10-9)
= (64÷8)×(10-14÷10-9)
= 8×10-5.
知识点
整数指数幂的运算法则
知4-讲
感悟新知
4
运算法则 公式
幂 的 运 算 同底数幂的乘法 同底数幂相乘,底数不变,指数相加 ① am·an=am+n(a ≠ 0,m,n 都是整数)
幂的乘方 幂的乘方,底数不变,指数相乘 (am)n=amn(a ≠ 0,m,n 都是整数)
知4-讲
感悟新知
幂 的 运 算 积的乘方 积的乘方等于各因 数分别乘方的积 ②(ab)n=anbn(a ≠ 0,b ≠ 0,n是整数)
同底数幂 的除法 同底数幂相除,底 数不变,指数相减 =am·a-n=am+(-n)=am-n(a ≠ 0,m,n 都是整数)
分式的 乘方 分式乘方等于分 子、分母分别乘方 =(a·b-1)n=an·(b-1)n=
an·b-n= (a ≠ 0,b ≠ 0,n 是整数)
知4-讲
感悟新知
特别提醒
同底数幂相除的运算法则被包含在公式①中,分式的乘方的运算法则被包含在公式②中.
感悟新知
知4-练
计算:
(1)(-m2n-3)·(3m-3n-2);(2)(2a-2)3b2÷4a-8b3;
解题秘方:按照先乘方,再乘除的顺序进行计算.
例8
感悟新知
知4-练
方法点拨
1. 幂的运算法则适用于任何整数指数幂.
2. 计算底数是分式的幂的运算时,先将分式形式的幂改写,分子的指数不变,分母的指数改为相反数,然后再按幂的运算法则计算.
3. 运算的结果有负指数的,要改写成分式的形式.
感悟新知
知4-练
解:(1)原式=-1×3×m2+(-3)×n-3-2=-3m-1n-5=-
(2)原式=8a-6b2÷4a-8b3=2a2b-1=
(3)原式=x-4y2·y-6x3÷x4y-4=x-4y2·x3y-6·x-4y4=
x-5y0=
课堂小结
整数指数幂
整数指数幂
同底数幂的除法
正整数指数幂
负整数指数幂
零次幂
科学计数法
结果
同课章节目录
